Amino acid racemization in Quaternary foraminifera from the Yermak Plateau, Arctic Ocean

Amino acid racemization (AAR) geochronology is a powerful tool for dating Quaternary marine sediments across the globe, yet its application to Arctic Ocean sediments has been limited. Anomalous rates of AAR in foraminifera from the central Arctic were reported in previously published studies, indicating that either the rate of racemization is higher in this area, or inaccurate age models were used to constrain the sediment ages. This study investigates racemization rates in foraminifera from three well-dated sediment cores taken from the Yermak Plateau during the 2015 TRANSSIZ (TRansitions in the Arctic Seasonal Sea Ice Zone) expedition on RV Polarstern. D and L isomers of the amino acids aspartic acid (Asp) and glutamic acid (Glu) were separated in samples of the planktic foraminifer Neogloboquadrina pachyderma and the benthic species Cassidulina neoteretis to quantify the extent of racemization. In total, 241 subsamples were analysed, extending back to marine oxygen isotope stage (MIS) 7. Two previously published power functions, which relate the extent of racemization of Asp and Glu in foraminifera to sample age are revisited, and a comparison is made between the ages predicted by these calibrated age equations and independent geochronological constraints available for the cores. Our analyses reveal an excellent match between ages predicted by a global compilation of racemization rates for N. pachyderma and confirm that a proposed Arctic-specific calibration curve is not applicable at the Yermak Plateau. These results generally support the rates of AAR determined for other cold bottom water sites and further highlight the anomalous nature of the purportedly high rate of racemization indicated by previous analyses of central Arctic sediments.

1 Introduction

Dating Quaternary marine sediments from the Arctic Ocean has been a long-standing problem, and a number of studies (e.g. Backman et al., 2004; Stein, 2011; Alexanderson et al., 2014) highlight the challenges of establishing firm chronologies for these sediments. Assigning ages for the various lithostratigraphic units in Arctic Ocean sediments is, however, of paramount importance as the development of accurate age models is key to contextualize Arctic palaeoceanography within Earth's climate system.

Amino acid racemization (AAR) geochronology was first applied specifically to Arctic Ocean sediments in the pioneering studies of Sejrup et al. (1984) and later in that of Macko and Aksu (1986). Sejrup et al. (1984) used AAR results to challenge the prevailing view of slow (mm kyr⁻¹) sedimentation rates (e. g. Clark, 1970) in the Arctic and warned that the existing age interpretations derived from bio- and magnetostratigraphy could be substantially flawed. On the other hand, Macko and Aksu (1986) found that AAR chronology of sediments from the Alpha Ridge supported the accepted ages established by the use of these two dating techniques, thus supporting arguments for slow sedimentation rates in this region. Due to the limitations – associated with small sample size and low temporal resolution – of these early studies, the application of AAR chronology for Arctic Ocean sediments decreased in the following years. However, major developments in AAR dating, such as the increased use of the more rapidly racemizing aspartic acid over isoleucine (e.g. Goodfriend et al., 1996) and the application of the reverse phase liquid chromatography to determine amino acid D∕L values in small samples (Kaufman and Manley, 1998) coupled with improvements in Arctic Ocean sediment chronostratigraphies (e.g. Jakobsson et al., 2001; Backman et al., 2008; O'Regan et al., 2008) have reignited the interest in AAR studies during the past decade.

Kaufman et al. (2008) related the extent of AAR in the polar foraminifera species Neogloboquadrina pachyderma, collected from various parts of the Arctic Ocean (Mendeleev Ridge, Lomonosov Ridge, Northwind Ridge), to sediment ages by developing a calibrated age equation for the past 150 kyr. This was followed by the study of Kaufman et al. (2013), who reported the results of AAR analysis of multiple foraminifera species from sediment cores taken in the Arctic, Atlantic, and Pacific oceans and defined a general rate of racemization at deep-sea sites. Both models relied on calibration of the rate of racemization of aspartic (Asp) and glutamic (Glu) acids by independent dating methods (such as radiocarbon dating and correlations with the orbitally tuned, stacked oxygen isotope record; Martinson et al., 1987), yet for the past 150 kyr, these two age equations produced significantly different ages for a given D∕L value. The global compilation of AAR showed that the rate of racemization in the Arctic Ocean was higher than expected in samples of N. pachyderma older than 35 ka, and this could not be explained by differences in the rate of AAR in N. pachyderma relative to other species. It remains to be seen whether the observed rates of racemization are anomalously high compared to other ocean basins or, alternatively, the age constraints for the studied Arctic Ocean cores are inaccurate. Sedimentary sequences with robust age control and satisfactory preservation of carbonate microfossils from the Arctic are required to further investigate this question.

Here we present the results of amino acid racemization analysis of planktic (N. pachyderma) and benthic (C. neoteretis) foraminifera from samples of three well-dated sediment cores from the Yermak Plateau. The rates of racemization in the two species are compared, and the Arctic-specific (Kaufman et al., 2008) and global (Kaufman et al., 2013) calibrated age equations are used to estimate the ages of the samples. The calculated ages are compared with those derived from age models constructed by combining ¹⁴C dating, oxygen isotope stratigraphy, and the correlation of environmental magnetic properties to the global benthic oxygen isotope record.

2 Materials and methods

2.1 Sample material and study area

The analysed foraminifera samples were taken from three sediment cores (PS92/0039-2, PS92/0045-2 and PS92/54-1) recovered from the Yermak Plateau during the TRANSSIZ (TRansitions in the Arctic Seasonal Sea Ice Zone) expedition (19 May to 28 June 2015) on the research icebreaker RV Polarstern (PS92) (Table 1 and Fig. 1).

Table 1 Sediment cores analysed in this study.

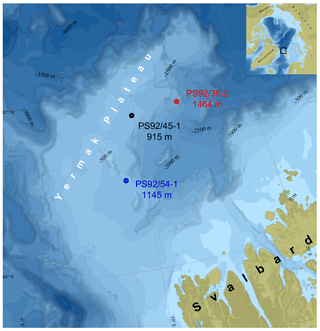
Figure 1 Locations of the studied cores and water depth at core sites. Basemap: IBCAO, Jakobsson et al. (2012).

The Yermak Plateau, located north of the Svalbard archipelago, lies at the gateway to the central Arctic Ocean, in an area characterized by the interaction between Atlantic and Arctic waters. The cold surface layer is dominated by the polar foraminifer N. pachyderma, which has highest abundances in the top 200 m (Carstens and Wefer, 1992; Carstens et al., 1997; Pados and Spielhagen, 2014; Greco et al., 2019). Cassidulina neoteretis is one of the dominant benthic species in sediments from the Yermak Plateau (Bergsten, 1994; Wollenburg and Mackensen, 1998; Wollenburg et al., 2004), and its abundance is often associated with the presence of Atlantic water (Polyak and Solheim, 1994; Ślubowska et al., 2005).

The cores were recovered from water depths between 915 and 1464 m – in the Upper Polar Deep Water – far below the core of the warmer Atlantic layer, which typically sits between depths of 200 and 500 m (Jones, 2001). Potential temperature and salinity profiles from nearby CTD (conductivity–temperature–depth) stations illustrate the relationship between the coring sites and the local water masses (Fig. 2).

Figure 2 Potential temperature and salinity profiles of CTD stations (PS92/39-8, 46-2, and 55-1) nearest to the coring sites. CTD stations 46-2 and 55-1 did not sample the water depths of cores 45-2 and 54-1; thus the markers approximate where they would sit on the CTD profiles.

2.2 Sample ages and quantification of age model uncertainties

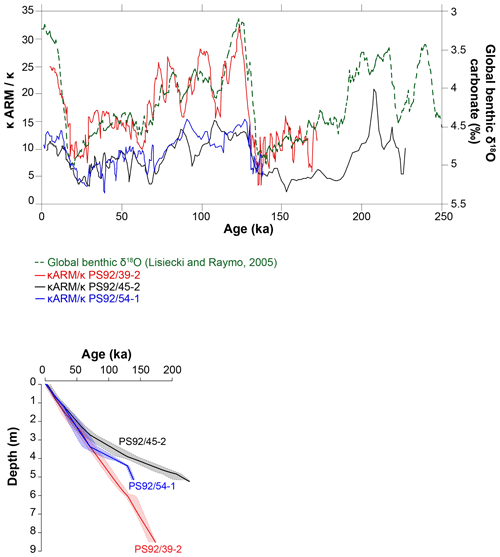
The age model of core PS92/39-2 was initially developed by Kremer et al. (2018), who used a combination of AMS ¹⁴C dates, sedimentological correlations and the occurrence of the benthic foraminifer Pullenia bulloides as a stratigraphic marker for event 5.1 (∼81 ka) in the polar North Atlantic (Haake and Pflaumann, 1989) and Arctic Ocean (Wollenburg et al., 2001). This age model was further developed by Wiers et al. (2019) by recalibrating the ¹⁴C dates, integrating additional carbon and oxygen isotope data from foraminifera, and applying a correlation between environmental magnetic parameters (ratio of anhysteretic remanent susceptibility and bulk magnetic susceptibility) with the global stacked benthic foraminifera δ¹⁸O_LR record of Lisiecki and Raymo (2005). Wiers et al. (2019) extended this method to cores PS92/45-2 and PS92/54-1 (Figs. 3 and 4). The ability to correlate environmental magnetic parameters to the global benthic δ¹⁸O record in late Quaternary sediments from the Yermak Plateau was first proposed by Xuan et al. (2012), who also utilized ¹⁴C dating and oxygen isotope measurements on planktic foraminifera.

To more rigorously provide a measure of the uncertainty inherent to the correlation-based age models, we applied an automated Monte Carlo algorithm for proxy-to-proxy stratigraphical alignment based on the assumption that changes in magnetic parameters (kARM/k, ratio of anhysteretic remanent susceptibility to bulk magnetic susceptibility) in our marine cores and variations in the δ¹⁸O_LR stack are virtually synchronous. The algorithm used here consists of a modified and improved routine that builds upon previous work by Malinverno (2013) and Muschitiello et al. (2015) and Muschitiello (2016) and that has been widely used for synchronization of different palaeoclimate archives (e.g. Wohlfarth et al., 2018; Muschitiello et al., 2019). The method was designed to obtain a sample of optimal alignment functions that relates depth in one record to age (or depth) in another. The median of the samples gives the best correlation and their variability provides a measure of the uncertainty associated with the alignment, whereby the alignment function will have larger uncertainties where the match between the proxy time series is poorly constrained. Further details on adjustment of the age–depth model of Wiers et al. (2019) are contained in Appendix A.

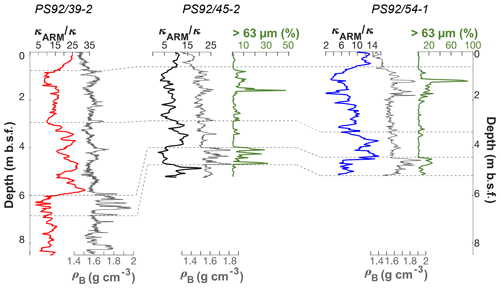
Figure 3 Lithostratigraphic correlation (on original depth scale) of sediment cores PS92/39-2, PS92/45-2, and PS92/54-1 based on Wiers et al. (2019). Dashed lines represent tie points. pB: bulk density.

Figure 4 The age–depth models (Wiers et al., 2019) of the cores in this study are based on correlation of environmental magnetic parameters (kARM/k) and the global benthic δ¹⁸O stack of Lisiecki and Raymo (2005).

2.3 Sample preparation and analytical procedure

Individual specimens of the foraminifera species N. pachyderma and C. neoteretis were picked from the >63 µm fraction of wet-sieved, oven-dried (4 h at 30 ^∘C), 2 cm thick slices of sediment samples from core depths in which tests of the two species were abundant. The sediment slices were taken from u-channel samples that had been used for palaeomagnetic measurements, implying that the samples came from the central parts of the cores. This resulted in a total of 10, 10, and 5 sampled stratigraphic levels in cores PS92/39-2, PS92/45-2, and PS92/54-1, respectively. Seven core depths were sampled for both N. pachyderma and C. neoteretis in cores PS92/45-2 and PS92/54-1. Core PS92/39-2 was only sampled for N. pachyderma.

The foraminifera tests were first cleaned by sonication (approximately 1 s) in a bath sonicator, then were immersed in 1 mL of 3 % H₂O₂ for 2 h. Some samples required up to 4 h of immersion for a complete removal of organic matter. The tests were rinsed 3 times with reagent grade water (grade I) and dried under a laminar flow hood. In order to create subsamples for each sampled core depth, 7–12 tests were picked (minimum 7 tests for C. neoteretis and minimum 10 for N. pachyderma) and placed in micro-reaction hydrolysis vials pre-sterilized by heating at 550 ^∘C. The number of subsamples within a sample was constrained by the number of available tests and their level of preservation in a particular sample. To dissolve the tests, 8 µL of 6 M HCl was added to the vials, and the solution was sealed under N₂ gas. The subsamples were hydrolysed at 110 ^∘C for 6 h in order to convert the original protein present in the tests into free amino acids. Following hydrolysis, the subsamples were evaporated in a vacuum desiccator. A total of 4 µL of 0.01 M HCl with 10 µM L-homoarginine spike was added to the evaporate, and the subsamples were then injected onto a high-performance liquid chromatograph (HPLC). All measurements were performed at the Amino Acid Geochronology Laboratory, Northern Arizona University. The HPLC instrumentation and procedure used are described by Kaufman and Manley (1998). Inter-laboratory standards (Wehmiller, 1984; Table 2) were analysed to monitor instrument performance.

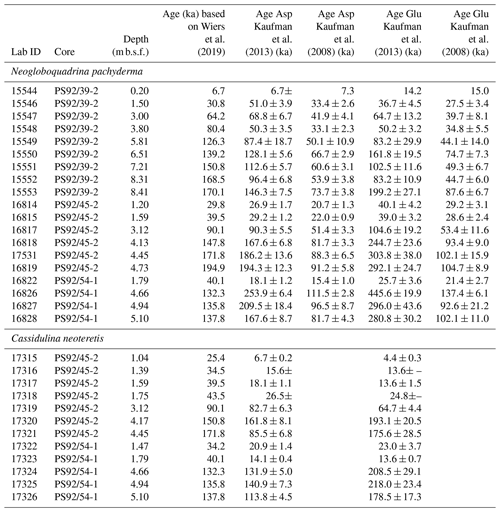
Table 2 Summary of aspartic acid and glutamic acid mean D∕L values (following data screening) and independent ages (based on Wiers et al., 2019) of samples analysed in this study; n: number of subsamples analysed; ex: number of excluded subsamples. Values in bold are mean D∕L values that show depth reversals. Interlaboratory standards (ILC A, B, C) analysed during the course of this study are also shown.

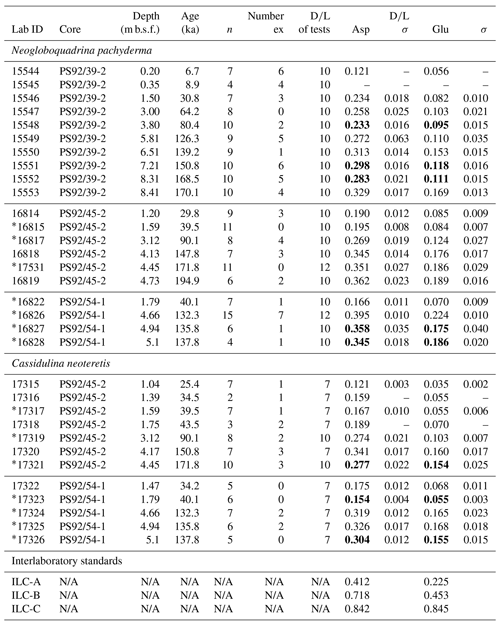
^∗ Samples marked with an asterisk are from core depths sampled for both Neogloboquadrina pachyderma and Cassidulina neoteretis. N/A: not applicable.

The extent of amino acid racemization was determined by analysing the peak-area ratio of D and L enantiomers (nine amino acids measured in total). Data analysis focused on Asp and Glu, as these amino acids are abundant in foraminifera protein and among the best-resolved chromatographically (e.g. Kaufman et al., 2013), and they provide the basis of previous calibrated age equations.

3 Results

A total of 32 foraminifera samples (10 from core PS92/39-2, 13 from core PS92/45-1, and 9 from core PS92/54-1) subdivided into 241 subsamples (average: 7.5 subsamples per sample) were analysed. The average number of foraminifera tests per subsample was 10.2 for N. pachyderma and 7.5 for C. neoteretis (Table 2). The results of amino acid analysis of all subsamples are contained in Table S1 in the Supplement.

In order to assess whether subsample size had a significant influence on the resulting D∕L values, a further 47 subsamples of the foraminifer N. pachyderma were taken, each with 20 individual tests, from stratigraphic depths already sampled (subsamples with 10 tests). The results of this analysis were then compared with 42 subsamples that comprised 10 tests. No statistically significant difference could be observed at the 0.01 probability level (the details of this analysis are contained in the Supplement).

Outliers were removed by following the screening process of Kosnik and Kaufman (2008):

1. Subsamples with L Ser/L Asp values greater than 0.8 were excluded, as this could be an indicator of contamination by modern amino acids.

2. The positive covariance of Asp and Glu acid D∕L values in foraminifera is well known (e.g. Hearty et al., 2004; Kosnik and Kaufman, 2008); subsamples that deviated from the expected trend were excluded (Fig. 5).

3. Remaining subsamples with D∕L Asp or D∕L Glu values outside the 2σ of the sample mean were rejected to emphasize the central tendency of the data.

This screening process resulted in the rejection of 68 subsamples, equivalent to 28.2 % of all subsamples. The overall rejection rate is higher than for most other studies as summarized by Kaufman et al. (2013), although in this study, subsamples from core 39-2 account for over half (53 %) of all rejected subsamples, despite only 35 % of all subsamples being taken from this core. Only 18.8 % – typical of previous studies – of the subsamples from core 45-2 was rejected, and this core provided 40 % of all subsamples.

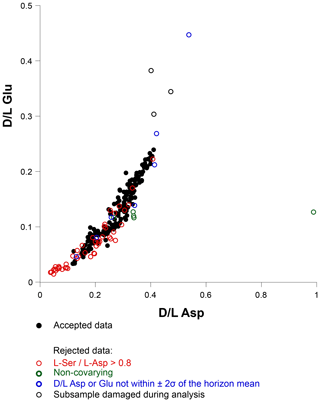
Figure 5 Covariance of aspartic acid and glutamic acid D∕L values in all subsamples. Open symbols indicate rejected results, with the rejection criterion indicated by the symbol colour.

Asp and Glu D∕L values show an increasing trend with depth for both foraminifera species (Fig. 6) in all cores. D∕L values of Asp and Glu in core PS92/39-2 are lower at equivalent depths below seafloor than compared to PS92/45-2 and PS92/54-1 when samples from below 3 m are considered. Eight of the 32 samples exhibit mean Asp D∕L values in reverse stratigraphic order (highlighted with bold in Table 2). Six of the reversed values overlap within 2σ errors with the sample from shallower depths, and only two mean Asp D∕L values from C. neoteretis samples in core PS92/45-2 (at 4.45 m) and in core PS92/54-1 (at 1.79 m) lack such an overlap. Mean D∕L Glu values also exhibit stratigraphically reversed values in these samples, with overlaps within the error range of the overlying sample.

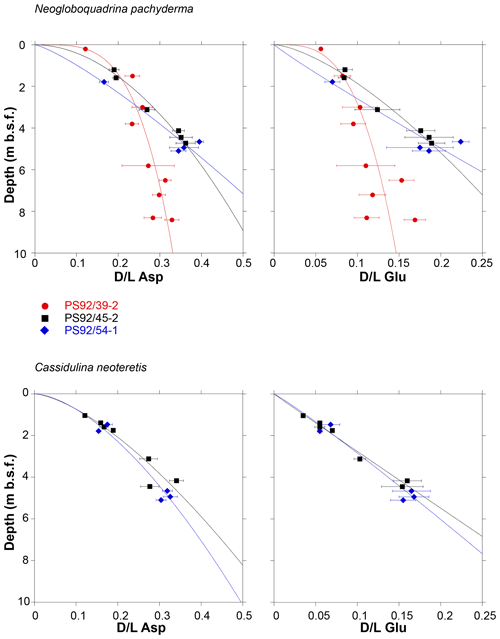
Figure 6 Extent of racemization (mean D∕L in aspartic acid and glutamic acid) in samples of N. pachyderma and C. neoteretis plotted against depth in sediment cores PS92/39-2, PS92/45-2, and PS92/54-1. Error bars represent ±1σ deviation from the sample mean. Least square regression lines (power fit) are shown for all cores. Data listed in Table 2.

Mean D∕L values of Asp and Glu are generally higher for N. pachyderma than for C. neoteretis for samples from the same depth (Table 2). This difference can be observed in both cores PS92/45-2 and PS92/54-1. It is difficult to quantify the differences in racemization rates between the two species, as little data are available for an extensive comparison, and some stratigraphic levels suffer from reversed D∕L values. However, as a basic approximation, a plot of N. pachyderma versus C. neoteretis mean D∕L values implies that Asp racemizes approximately 17 % faster in N. pachyderma than in C. neoteretis, while Glu racemizes about 23 %–26 % faster in N. pachyderma (Fig. 7).

4 Discussion

4.1 Relation between D∕L values and depth and inter-specific differences

The extent of racemization generally increases with depth in both N. pachyderma and C. neoteretis samples, and this conforms to the expected diagenetic behaviour of amino acids in foraminifera. Eight samples have stratigraphically reversed mean D∕L Asp and Glu values, but six of these values overlap within the 2σ uncertainty envelope with the overlying sample.

For a given sediment depth, the extent of racemization in N. pachyderma samples is lower in PS92/39-2 below 3 m than in the other two cores (Fig. 6). This is consistent with the higher sedimentation rates in PS92/39-2 below 3 m, compared to the other two cores, based on the independent age control of Wiers et al. (2019).

Differences in the rates of AAR (16 % for Asp and 23 %–26 % for Glu – Fig. 7) between N. pachyderma and C. neoteretis tests from the same depths are similar to those documented in other AAR studies (e.g. King and Neville, 1977; Kaufman et al., 2013). Little is known about the extent and causes of the differences in racemization rates in these two species, but differences of similar magnitude between D∕L values of different taxa were previously reported in the literature. For example, Kaufman et al. (2013) found that Asp racemized 12 %–16 % faster in Pulleniatina obliquiloculata than in N. pachyderma. As N. pachyderma and C. neoteretis are amongst the most commonly occurring planktic and benthic foraminifera species in the Arctic, the quantification of the relative rates of racemization between the two species will aid future AAR studies in the Arctic and could be augmented by future laboratory heating experiments.

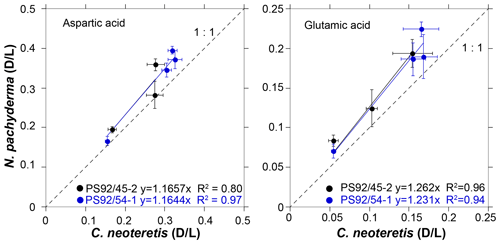
Figure 7 Extent of racemization (D∕L) for aspartic and glutamic acids in N. pachyderma versus C. neoteretis samples from cores PS92/45-2 and PS92/54-1, with linear regression and line of equality.

Stratigraphically reversed D∕L Asp values, which do not overlap within the 2σ uncertainty, only appear in C. neoteretis samples. One such reversal is in core PS92/45-2, in sample UAL17321 from 4.45 m core depth (total core length: 5.20 m). In this sample the mean D∕L Asp value of 0.277 (σ=0.022) is essentially equal to the mean value of 0.274 (σ=0.021) from 3.12 m depth. It is difficult to explain the origin of the stratigraphically reversed mean values in the C. neoteretis samples. Sediment mixing (e.g. bioturbation, reworked material entrained in sea ice) offers one possible explanation and may account for reversals on decimetre scales, but it seems less likely that metre-scale downward mixing – which would be required to explain the reversal discussed in PS92/45-2 – occurs. Icebergs are capable of extensive sediment reworking, but shipboard parasound and multibeam data show that the coring sites were free from iceberg scouring. The excellent correlation between the records precludes the possibility of large erosional events that could have removed or reworked sediments.

However, the small number (7) of foraminifera tests used in subsamples of C. neoteretis could also make the D∕L values more susceptible to variations in individual tests. For example, Lougheed et al. (2018) recently highlighted the large heterogeneity in the age distribution of foraminifera obtained from discrete depth intervals using ¹⁴C dating of single foraminifera.

4.2 Relation between D∕L values and sample age

A biplot of D∕L values against sample ages reveals that, as expected, the rate of Asp and Glu racemization is higher in younger samples and decreases with sample age as the reaction progresses towards equilibrium (Fig. 8). D∕L values increase in a predictable manner over time as shown by least square regression power curves fitted to the mean D∕L Asp and Glu values for each of the cores. An exceptionally good fit for N. pachyderma samples is achieved in core PS92/45-2 (with R² values of 0.99 and 0.98 for D∕L Asp and Glu, respectively; for individual regression lines see Fig. S1). In C. neoteretis samples, both Asp and Glu appear to racemize at similar rates in cores PS92/45-2 and PS92/54-1. Dissimilar D∕L Asp and Glu value between samples of comparable ages from different cores may originate from differences in sedimentation rates between the cores, variable post-depositional environmental factors, including differences in geothermal gradients, or variable diagenetic processes. These are discussed in more detail below.

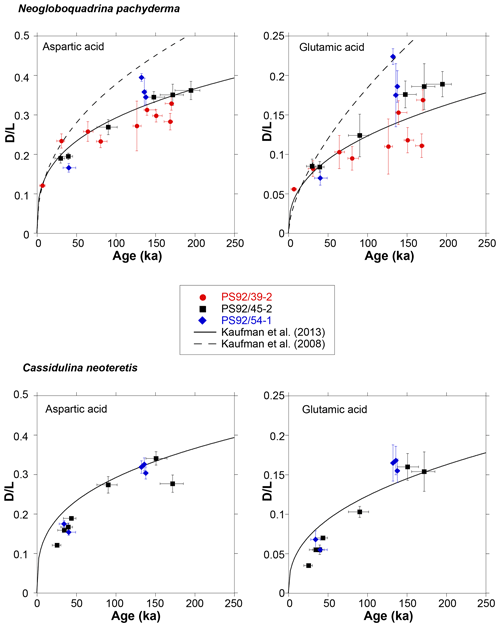
Figure 8 Mean D∕L values of aspartic and glutamic acids plotted against the independent ages of Wiers et al. (2019) for N. pachyderma and C. neoteretis samples from cores PS92/39-2, PS92/45-2, and PS92/54-1. Ages predicted (based on D∕L Asp and Glu values) by the globally calibrated age equation of Kaufman et al. (2013) and the Arctic-specific age equation (Kaufman et al., 2008) are also displayed for reference. Error bars represent ±1σ deviation from the mean D∕L value of the sample and age uncertainty.

4.3 Palaeotemperature and other possible effects

In monospecific foraminifera samples, the rate of racemization is often considered to be primarily controlled by the integrated post-depositional temperature (Kaufman et al., 2013). Therefore, if the D∕L value and age of a sample are known, the AAR age equation can be solved for palaeotemperatures. Here we provide a rudimentary estimation of the difference in the effective diagenetic temperatures required to account for the offset between known-age-equivalent D∕L values between the coring sites. To achieve this, we relied on the temperature equation originally derived by Kaufman (2006) using simple power law kinetics for Asp in the foraminifera species, Pulleniatina obliquiloculata, and increased the D∕L values of our N. pachyderma samples by 16 % to account for the lower rate of racemization in this taxon, as established by Kaufman et al. (2013). For comparison between the three core sites, we determined the approximate D∕L Asp values predicted by power-fit functions for each core at 150 ka; then the effective diagenetic temperatures integrated over the past 150 kyr were derived from the temperature equation. The absolute derived temperatures need to be interpreted with caution, as no formal assessment of the racemization kinetics in N. pachyderma and an assessment of the uncertainties associated with these were completed. Furthermore, there are a number of complicating factors to these temperature estimates that are discussed below. However, relative temperature differences between the sites are likely still meaningful. The results imply that temperature differences (ΔT) of ∼1.6–4.0 ^∘C are required to account for the observed differences in racemization rates between the cores over the past 150 kyr (Table 3). Details on palaeotemperature calculations are contained in the Supplement.

Table 3 Approximate effective diagenetic temperatures at the three core sites integrated over the past 150 kyr (^∘C).

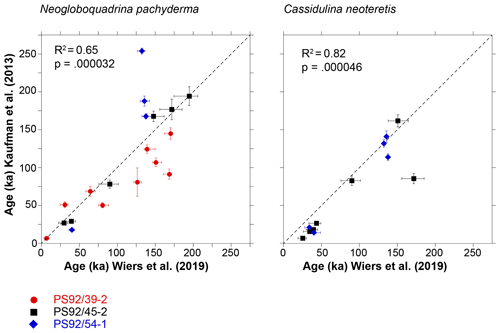
Figure 9 Comparison of sample ages for the two foraminifera taxa as predicted by the globally calibrated age equation of Kaufman et al. (2013) based on D∕L Asp values and ages assigned to the samples based on the age model developed by Wiers et al. (2019), with line of equality.

It is important to emphasize that AAR palaeotemperature estimates can only provide a measure of the long-term average post-depositional temperature, rather than the temperature of the water during calcification. The estimated difference in effective diagenetic temperatures between PS92/39-2 and PS92/54-1 (4±1.6 ^∘C) cannot be easily accounted for by changes in bottom water temperatures alone. Modern bottom water temperatures at the three coring locations are relatively similar (between −0.25 and −0.76 ^∘C) (Table 1), although we do not know how similar these remained across glacial cycles. Presently the coring sites are beyond the reach of the warm (>0.5 ^∘C) Atlantic layer (Fig. 2), which would need to be at significantly greater depths to generate such a large spread in the effective diagenetic temperatures of the coring sites. It is unclear how this could have happened in the past, and we do not see it as a plausible explanation for the apparent differences in calculated effective diagenetic temperatures.

Apart from differences in bottom water temperatures, differences in the geothermal gradient among sites could also impact the palaeotemperature signal. Unfortunately, no direct measurements of heat flow were obtained at the coring stations during TRANSSIZ and existing heat flow data from the Yermak Plateau are relatively sparse (Okay and Crane, 1993; Shephard et al., 2018). Existing measurements do indicate that regions of the Yermak Plateau are characterized by relatively high heat flow (>100 mW m⁻²), but with considerable spatial variability. Most measurements lie in the range of 50 to 100 mW m⁻² (Shephard et al., 2018). If we use a thermal conductivity of 1.17 W mK⁻¹, reported from measurements on a core obtained from the Yermak Plateau (Shephard et al., 2018), heat flow of 50–100 m Wm⁻² translates into geothermal gradients of 43 to 85 ^∘C km⁻¹ (0.043 to 0.085 ^∘C m⁻¹). At a depth of 6 m below the seafloor, this range of geothermal gradients would amount to a present-day in situ temperature difference of only 0.25 ^∘C. Thus, it also seems unlikely that local heat flow variations would significantly affect rates of racemization at the shallow sediment depth of these samples.

Table 4 Independent sample ages based on Wiers et al. (2019) and sample ages and uncertainties based on the globally calibrated age equation of Kaufman et al. (2013) and the Arctic-specific age equation of Kaufman et al. (2008) based on mean D∕L values of Asp and Glu.

Sejrup and Haugen (1994) have theorized that variations in post-depositional microbial activity could have a profound impact on AAR and that the extent of microbial activity is related to sedimentation rates. Shells deposited in settings with low sedimentation rates could have been exposed longer to microbial activity at the seabed than shells that were buried rapidly and therefore more rapidly removed from the taphonomically active zone. Such increased exposure could result in a higher degree of protein and amino acid degradation in the early diagenetic phase, giving rise to higher initial D∕L values. The sedimentation rate in core PS92/39-2 is estimated to be around 4.5 cm kyr⁻¹ during marine oxygen isotope stage (MIS) 5 (assigned to the depth interval between 3.5–6 m), 2.5 times that of the sedimentation rate at the other two core sites (Table 3). The comparatively lower D∕L values in core PS92/39-2 could reflect the faster burial and thereby better preservation of indigenous proteins in tests from the 3.5–6 m depth interval, yet the exact mechanisms of microbially mediated racemization remain unresolved. Currently we lack sufficient data to more fully explore the reasons for inter-site offsets in the AAR rates.

4.4 Comparing AAR age models

In order to assess the validity of the previously derived Arctic-specific (Kaufman et al., 2008) and globally calibrated (Kaufman et al., 2013) age equations at the Yermak Plateau, ages predicted by the two models were generated using the mean D∕L Asp and Glu values from N. pachyderma and C. neoteretis tests in this study (Table 4). No ages using the Arctic-specific age equation were generated for C. neoteretis samples, as this calibration is based on AAR in N. pachyderma tests only. Ages predicted by the models were plotted against the corresponding D∕L values and displayed for reference in the biplot of D∕L values against sample age (Fig. 8). Age uncertainties were derived using the intra-sample variability (±1σ) propagated through the age equations.

Modelled ages generated using the globally calibrated age equation of Kaufman et al. (2013) and mean D∕L Asp values in N. pachyderma are most similar to the sample ages of Wiers et al. (2019) (Fig. 8). The Arctic-specific age equation of Kaufman et al. (2008) results in significantly younger ages than those based on the Wiers et al. (2019) age model (Fig. 8). This implies that the Arctic-specific age equation cannot be used to constrain the ages of sediments from the Yermak Plateau.

These results generally support the rates of AAR determined for other deep-sea (cold bottom water) sites, further highlighting the peculiar high rate of racemization indicated by previous analyses of central Arctic sediments. For example, previously published (Kaufman et al., 2008) mean D∕L Asp values for N. pachyderma samples from a central Arctic core from the Lomonosov Ridge (96/12-1PC) are around 0.4 for samples dated to 85–123 ka. The globally calibrated age equation predicts approximate ages of 263 kyr for this D∕L Asp value (with ±15.8 kyr error, assuming an uncertainty of 6%, typical of mean D∕L values in this study), and samples with similar D∕L values from the Yermak Plateau would date to around 232±14 ka. The considerable differences could indicate different post-depositional temperatures, variable sedimentation rates, diagenetic processes, issues with sample handling, storage, and processing or may point towards errors in the existing age models of central Arctic sediments. Further studies are clearly required to investigate these options.

AAR ages based on D∕L Asp values and the globally calibrated AAR curve strongly correlate with the independent ages of Wiers et al. (2019) for both species (Fig. 9); however, there is a significant scatter in AAR ages older than ∼130 ka. Excluding all samples with stratigraphically reversed D∕L Asp values (regardless of whether there is an overlap within 2σ errors or not) increases the correlation coefficient (r) to 0.96 in N. pachyderma and to 0.99 in C. neoteretis samples. While well-correlated, the globally calibrated age equation slightly (∼ on average 2 %) underestimates the ages of N. pachyderma samples, with the highest level of agreement between the ages observed in core PS92/45-2. The ages of C. neoteretis samples are mostly underestimated – on average by 32 %. This is expected considering the lower racemization rates of C. neoteretis observed in this study (approximately 16 % slower than N. pachyderma). Both sets of data are coupled with high values of scatter, with differences between the modelled ages and the ages based on Wiers et al. (2019) reaching over 50 % of the sample age in some cases. Nevertheless, the globally calibrated age equation provides a reliable age approximation for our Arctic Ocean sediments, when D∕L Asp values from N. pachyderma samples are utilized.

5 Conclusions

The extent of racemization of Asp and Glu increases with increasing age in both N. pachyderma and C. neoteretis samples and is higher in N. pachyderma than in C. neoteretis from the same stratigraphic levels.

The globally calibrated age equation of Kaufman et al. (2013) provides a reliable age control for sediments from the Yermak Plateau. The Arctic-specific calibrated age equation of Kaufman et al. (2008) does not support the independent age–depth model in this area, and is not applicable to sediments from the Yermak Plateau.

Ages calculated with the globally calibrated age equation of Kaufman et al. (2013) show the highest level of agreement with sample ages when D∕L Asp values from N. pachyderma samples are used. Ages obtained using the globally calibrated age equation and D∕L Asp values in C. neoteretis samples consistently appear younger (on average by 32 %) than the independent ages, as expected given the lower rate of AAR in this species.

The results highlight the need for further studies to test and explain the origin of the higher racemization rates in foraminifera reported in previous studies from central Arctic sediments.

Appendix A

Prior to alignment, the kARM/k time series and the δ¹⁸O_LR stack were rescaled between −1 and 1 to improve comparability. The alignment function is then inferred at any point on the sediment core depth scale by a linear interpolation between three proposed depth–age models: a starting node, an ending node, and a perturbed node at a random location between the starting and ending nodes. The nodes strictly follow depth–age paths that do not violate the principle of superposition in order to ensure a monotonic relationship between the depth of the sediment core and the age of the δ¹⁸O_LR stack. The algorithm determines the set of nodes that give a good alignment between the kARM/k time series and the δ¹⁸O_LR stack as defined by a small residual standard deviation and a high coefficient of correlation. As an additional condition, we require that the gradient of the depth–age alignment function should be reasonably smooth, hence assuming that at our coring sites sedimentation rates have not undergone excessively rapid shifts or large fluctuations.

The requirement of a good match between the kARM/k records and the δ¹⁸O_LR stack and a smooth alignment function is here devised in a Bayesian formulation sensitive to specification of a conjugate prior distribution and a conjugate likelihood distribution of the alignment function. The priors specify (i) the age distribution of the first and last kARM/k values on the δ¹⁸O_LR age scale (here set as non-informative uniform ranging over 10 kyr) and (ii) the degree of autocorrelation of the sedimentation rates (here set as truncated uniform between −50 % and +50 %). The latter dictates how much the accumulation rate of a particular depth depends on the depth above it, which in turn controls the gradient of the depth–age alignment function. The likelihood distribution of the alignment function weighs the competing needs of small standard deviations of the data residuals and a high correlation between the kARM/k and the δ¹⁸O_LR values. Finally, a conditional posterior distribution of alignment functions proportional to the product of prior and likelihood is inferred. Calculation of the posterior proceeds by sampling an initial value for each unknown parameter from the associated prior distributions using a reversible jump Markov chain Monte Carlo (MCMC) sampling (Vihola, 2012). In the alignment problem posed here, the automated MCMC method consists of the following steps. Starting from an initial age for the first and last kARM/k values on the δ¹⁸O_LR timescale that defines an initial match between the kARM/k and δ¹⁸O_LR time series, and by setting an initial value for the rate of sedimentation, it continues by

1. proposing a new “candidate” alignment function by adding a new depth–age node at a random location between the starting and ending nodes along the depth scale of the sediment core.

2. accepting or rejecting the candidate alignment function according to its posterior probability using the Metropolis–Hastings algorithm (Metropolis et al., 1953; Hastings, 1970), whereby the posterior probability is higher for alignment functions that yield a closer match (i.e. a smaller residual standard deviation and a high coefficient of correlation).

3. Repeat from step 1 for 10⁶ iterations.