Novel method for determining ²³⁴U–²³⁸U ages of Devils Hole 2 cave calcite (Nevada)

Uranium–uranium (²³⁴U–²³⁸U) disequilibrium dating can determine the age of secondary carbonates over greater time intervals than the well-established ²³⁰Th–²³⁴U dating method. Yet it is rarely applied due to unknowns in the initial δ²³⁴U (δ²³⁴U_i) value, which result in significant age uncertainties. In order to understand the δ²³⁴U_i in Devils Hole 2 cave, Nevada, we have determined 110 δ²³⁴U_i values from phreatic calcite using ²³⁰Th–²³⁴U disequilibrium dating. The sampled calcite was deposited in Devils Hole 2 between 4 and 590 ka, providing a long-term look at δ²³⁴U_i variability over time. We then performed multi-linear regression among the δ²³⁴U_i values and correlative δ¹⁸O and δ¹³C values. The regression can be used to estimate the δ²³⁴U_i value of Devils Hole calcite based upon its measured δ¹⁸O and δ¹³C values. Using this approach and the measured present-day δ²³⁴U values of Devils Hole 2 calcite, we calculated 110 independent ²³⁴U–²³⁸U ages. In addition, we used newly measured δ¹⁸O, δ¹³C, and present-day δ²³⁴U values to calculate 10 ²³⁴U–²³⁸U ages that range between 676 and 731 ka, thus allowing us to extend the Devils Hole chronology beyond the ²³⁰Th–²³⁴U-dated chronology while maintaining an age precision of ∼ 2 %. Our results indicate that calcite deposition at Devils Hole 2 cave began no later than 736 ± 11 kyr ago. The novel method presented here may be applied to future speleothem studies in similar hydrogeological settings, given appropriate calibration studies.

1 Introduction

The mid-20th century discovery of ²³⁴U–²³⁸U disequilibrium in natural waters (Cherdyntsev, 1955; Isabaev et al., 1960; Thurber, 1962) unlocked a new geochronometer for sediments in marine and freshwater settings. The greatest limitation of the ²³⁴U–²³⁸U dating method, however, lies in the uncertainty of the initial δ²³⁴U (δ²³⁴U_i), as shown in Eq. (1):

$$\begin{array}{}\text{(1)}& {\mathit{\delta }}^{\mathrm{234}}{\mathrm{U}}_{\mathrm{i}}={\mathit{\delta }}^{\mathrm{234}}{\mathrm{U}}_{\mathrm{p}}\times e^{{\mathit{\lambda }}_{\mathrm{234}}T},\end{array}$$

where δ²³⁴U_p refers to the present δ²³⁴U value, δ²³⁴U_i refers to the δ²³⁴U value at the time of deposition, λ₂₃₄ is the decay constant of ²³⁴U, and T refers to the time elapsed since deposition. In marine settings, δ²³⁴U_i can be approximated using the known excess ²³⁴U activity in seawater. Ku (1965) was the first to test the ²³⁴U–²³⁸U geochronometer in marine sediments. Although this method has been applied successfully in marine-sourced secondary carbonates (Veeh, 1966; Bender et al., 1979; Ludwig et al., 1991), it has largely been limited by the potential mobility of U following deposition, as observed in mollusks (Kaufman et al., 1971) and corals (Bender et al., 1979; Gallup et al., 1994).

In freshwater settings, constraining the δ²³⁴U_i of secondary carbonates is further complicated by the fact that, in contrast to seawater, terrestrial surface and groundwaters exhibit a wide spatial and temporal variability in δ²³⁴U. Uncertainties in determining past δ²³⁴U_i result in ²³⁴U–²³⁸U age uncertainties that are orders of magnitude greater than those common for ²³⁰Th–²³⁴U disequilibrium dating. ²³⁰Th–²³⁴U dating has thus remained the preferred method for determining the age of secondary carbonates that have been deposited between the modern day and ∼ 600 ka, at which secular equilibrium between ²³⁰Th and ²³⁴U has been nearly restored. However, with a firm understanding of past source-water δ²³⁴U_i, the ²³⁴U–²³⁸U disequilibrium method is a powerful geochronometer that can reach deeper in time than ²³⁰Th–²³⁴U disequilibrium dating (e.g., Gahleb et al., 2019).

The Devils Hole (DH) and neighboring Devils Hole 2 (DH2) caves are ideal settings for the study of groundwater δ²³⁴U_i variations over time. The walls of both steep fractures are coated with thick (up to ∼ 90 cm) layers of calcite deposits that have precipitated subaqueously at a rate of approximately 1 mm per 1000 years (Ludwig et al., 1992; Moseley et al., 2016). Small variations in calcite δ²³⁴U_i (1851 ‰–1616 ‰) over the last 500 kyr have been precisely determined by Ludwig et al. (1992) and Wendt et al. (2020). Due to the high initial ²³⁴U excess in DH and DH2 calcite (mean δ²³⁴U_i=1750 ‰), the ²³⁴U–²³⁸U disequilibrium method can theoretically determine the age of DH and DH2 calcite as old as 2.5 Ma.

Ludwig et al. (1992) were the first to calculate ²³⁴U–²³⁸U ages from DH calcite. To do so, they derived the δ²³⁴U_i value from 21 ²³⁰Th–²³⁴U ages between 60 and 350 ka. From this dataset, they calculated the median δ²³⁴U_i value (1750 ‰) and associated uncertainty (±100 ‰); the latter was derived from the range of δ²³⁴U_i over the selected time period. Using this δ²³⁴U_i value, 18 ²³⁴U–²³⁸U ages were calculated. The ages ranged between 385 and 568 ka with mean uncertainties of 20 kyr (3 %–5 % relative uncertainty) (Ludwig et al., 1992).

Building upon the pioneering work of Ludwig et al. (1992), we aim to decrease the uncertainties of DH and DH2 δ²³⁴U_i in order to improve the precision of ²³⁴U–²³⁸U ages. A negative correlation between DH δ²³⁴U_i and δ¹⁸O, and a positive correlation between δ²³⁴U_i and δ¹³C, is observed over the last 500 kyr (Ludwig et al., 1992). Similar correlative patterns were obtained over the last 200 kyr using separate drill cores from DH2 (Moseley et al., 2016) and were shown to be independent of U concentrations (Fig. S1; Wendt et al., 2020). In this study, we show that by accounting for changes in δ²³⁴U_i with respect to δ¹⁸O and δ¹³C, we can reduce the uncertainty in δ²³⁴U_i by 40 %, thereby reducing the uncertainty in ²³⁴U–²³⁸U ages to about ± 13 kyr within a several-hundred-thousand-year range. We then use this method to calculate the age of calcite that was deposited in DH2 prior to (older than) the limit of ²³⁰Th–²³⁴U disequilibrium dating (∼ 600 ka). Doing so allows us to extend the radiometric chronology and determine the time at which calcite first deposited in DH2.

1.1 Regional setting

The DH and DH2 caves are located 100 m apart in a detached area of Death Valley National Park in southwest Nevada (36^∘25^′ N, 116^∘17^′ W; 719 m above sea level). Bedrock of the study area is composed of carbonates from the Bonanza King Formation of middle and late Cambrian age (Barnes and Palmer, 1961). The caves follow a pair of deep, planar, steeply dipping fault-controlled open fissures roughly 5 m wide, 15 m long, and at least 130 m deep (Riggs et al., 1994). Evidence for the tectonic origin of these caves includes the spreading and the orientation of their planar opening, which is perpendicular to the northwest–southeast principal stress direction that has prevailed in this part of the Great Basin for the last 5 Myr (Carr, 1974). Parts of these extensional fractures were later modified by condensation corrosion (Dublyansky and Spötl, 2015).

DH and DH2 both intersect the water table of the Ash Meadows Groundwater Flow System (AMGFS), which is a large (∼ 12 000 km²) aquifer hosted in Paleozoic limestone (Winograd and Thordarson, 1975). The AMGFS is primarily recharged by infiltration of snowmelt and rainfall in the upper elevations of the Spring Mountains (∼ 500 mm a⁻¹; Winograd and Thordarson, 1975; Thomas et al., 1996; Winograd et al., 1998; Davisson et al., 1999). Quaternary extensional tectonics in this area has produced an underground network of open fractures which contribute to the high transmissivity of the aquifer. Previous studies suggest groundwater transit times of <2000 years from the Spring Mountains to DH/DH2 caves (Winograd et al., 2006). Due to the long flow path (>60 km) and prolonged residence time, the groundwater flowing southwest through both caves is very slightly supersaturated with respect to calcite (SI of 0.2; Plummer et al., 2000). The caves are <1.5 km upgradient from a line of springs that represent the primary discharge area of the AMGFS.

Calcite has been continuously depositing as dense mammillary crusts on the submerged walls of DH and DH2 over much of the last 1 Myr at a very slow rate of roughly 1 mm kyr⁻¹ (Ludwig et al., 1992; Winograd et al., 2006; Moseley et al., 2016). The thickness (≤90 cm) of mammillary calcite crusts implies a long history of calcite-supersaturated groundwater. Regional groundwater transmissivity is maintained despite calcite precipitation due to active extensional tectonics (Riggs et al., 1994).

2 Methods

A 670 mm long core was drilled from the hanging wall of DH2 cave at +1.8 m relative to the modern water table (r.m.w.t.). The first 654 mm of the core consist of calcite; the last 16 mm of the core consist of bedrock. The core consists of two types of calcite: mammillary calcite and folia. For a full description of the petrographic and morphological differences between both forms of calcite, see Wendt et al. (2018). Briefly, mammillary calcite precipitates subaqueously, while folia forms at the water table in a shelf-like formation. The presence of folia in the core is an indicator of the paleo-water table near +1.8 m r.m.w.t. at the time of deposition.

The selected core was cut longitudinally and polished. The core was surveyed for growth hiatuses and features indicative of changing deposition mechanisms and rates (such as folia). Folia was identified at 77.7–97.4 mm (as reported in Moseley et al., 2016), 171.4–199.2, 209.4–229.0, and 305.0–323.0 mm (distances are reported from top of the calcite sequence). In addition, a growth hiatus was discovered between 587.4 and 589.0 mm (Fig. S2).

The mammillary calcite portions of the core were ²³⁰Th–²³⁴U dated at regular intervals (n=110). As described in Moseley et al. (2016), folia calcite cannot be reliably dated. Results for the first 91 ²³⁰Th–²³⁴U ages were published by Moseley et al. (2016) and Wendt et al. (2020). Nine additional ²³⁰Th–²³⁴U ages were measured between 351.0 and 562.0 mm using identical methodology to the aforementioned publications. The purpose of additional ²³⁰Th–²³⁴U ages is to extend the DH2 chronology to the near limit of ²³⁰Th–²³⁴U dating (about 600 ka). Between 608.2 and 652.0 mm, 10 new δ²³⁴U measurements were collected for this study. To do so, calcite powders were hand drilled at approximately 1 cm intervals and spiked following the ²³⁰Th–²³⁴U dating method cited above. The U aliquots were then extracted and measured following the methods described in Cheng et al. (2013). Chemical blanks were measured with each set of 10–15 samples and were found to be negligible (<50 ag for ²³⁰Th, <100 ag for ²³⁴U, and <1 pg for ²³²Th and ²³⁸U).

Samples for stable isotope measurements were micromilled continuously at 0.1–0.2 mm intervals along the core axis between 0 and 158 mm and presented by Moseley et al. (2016). The values of two to three stable isotope measurements (0.1–0.2 mm in width) were averaged in order to pair with ²³⁰Th–²³⁴U subsamples, which averaged 0.3 to 0.5 mm in width. Between 169.8 and 652.0 mm, 66 new stable isotope samples were micromilled at the location of each ²³⁰Th–²³⁴U and δ²³⁴U measurement published by Wendt et al. (2020). Similarly, two to three stable isotope measurements were averaged to encompass the width of U isotope subsamples. Calcite powders were analyzed using a Delta V plus isotope ratio mass spectrometer interfaced with a Gasbench II. Values are reported relative to Vienna Pee Dee Belemnite (VPDB) with 1σ precisions of 0.06 ‰ and 0.08 ‰ for δ¹³C and δ¹⁸O, respectively.

A statistical model was built to predict δ²³⁴U_i values based on the correlation observed between measured δ²³⁴U_i and stable isotope values from 4 to 590 ka. To calculate the correlation analysis for unevenly spaced time series, we chose the Fortran 90 program PearsonT3, which can provide the 95 % calibrated confidence intervals (Olafsdottir and Mudelsee, 2014). OriginPro software (version 2015) was used to conduct the regression analyses (Moberly et al., 2018; see detailed description in the Supplement). Several types of models fitted with linear, quadratic, and cubic regression methods were built. The model that provided the best estimate of the measured δ²³⁴U_i values was selected. Using this model, a statistically derived (SD) δ²³⁴U_i value can be generated based on known δ¹⁸O and δ¹³C values. The SD δ²³⁴U_i and measured δ²³⁴U_p can then be used to calculate ²³⁴U–²³⁸U ages (Eq. 1). The ²³⁴U decay constant of 2.82206 ± 0.00302×10⁻⁶ a⁻¹ (Cheng et al., 2013) was used. We validated our methodology and uncertainty estimates by comparing ²³⁰Th–²³⁴U and ²³⁴U–²³⁸U dates obtained for samples younger than 590 ka.

Using this dataset, we calculated 120 ²³⁴U–²³⁸U ages for samples in total. With these ages as input, we calculated an age model using the OxCal version 4.2 Bayesian statistical software (Bronk Ramsey and Lee, 2013). Age models were calculated under deposition sequence “P” with the k parameter set to 0.1 (Bronk Ramsey and Lee, 2013). The positions of growth hiatuses, including folia calcite, were incorporated into the age model as growth boundaries.

3 Results

The new ²³⁰Th–²³⁴U disequilibrium ages (denoted in subsequent text as ²³⁰Th ages for simplicity) are in stratigraphic order within uncertainties. ²³⁸U and ²³²Th concentrations fall within the range of previous data published by Moseley et al. (2016) and Wendt et al. (2020). The time–depth consistency and reproducibility of ages argue against open-system processes. The existence of an approximately 67 kyr growth hiatus between 587.4 and 589.0 mm is supported by ²³⁴U–²³⁸U ages (see the Supplement).

In this study, we split the δ²³⁴U_i dataset into three sections (4–309, 309–355, and 355–590 ka). The sections were divided according to the level of uncertainty in δ²³⁴U_i derived from ²³⁰Th ages (see Tables 1 and S4). The average δ²³⁴U_i was the same within uncertainties regardless of how we grouped the data, implying no detectable trend in δ²³⁴U_i with time.

Table 1 Statistics of δ²³⁴U_i with different temporal groupings.

DH2 oxygen isotope values reveal a negative correlation with δ²³⁴U_i over the last 590 kyr (0–578 mm along the core axis; $r=-\mathrm{0.52}$ with the 95 % confidence interval of [−0.81; −0.06]), whereas carbon isotopes reveal a positive correlation (r=0.71 with the 95 % confidence interval of [0.57; 0.81]; Fig. 1 and Table 2). The interpretation of δ¹⁸O and δ¹³C in DH and DH2 calcite has been extensively discussed in Winograd et al. (1988, 1992, 2006), Coplen et al. (1994), and Moseley et al. (2016). DH/DH2 δ¹⁸O is a reflection of meteoric precipitation at the principal recharge zones of the AMGFS. Modern meteoric δ¹⁸O varies seasonally by >10 ‰ in southern Nevada (Ingraham et al., 1991). Winter precipitation (−12 ‰ to −14 ‰ Vienna Standard Mean Ocean Water; VSMOW) is sourced from the Pacific and provides the dominant fraction (∼ 90 %) of aquifer recharge, while summer precipitation (0 ‰ to −3 ‰ VSMOW) is sourced from monsoonal systems from the gulfs of Mexico and California (see Winograd et al., 1998, for details). We interpret past variations in DH/DH2 δ¹⁸O to be the result of (i) changes in temperature and variations in the path length of moisture transport through Rayleigh fractionation processes, (ii) changes in δ¹⁸O values at moisture source regions, and (iii) changes in the relative contributions of summer versus winter precipitation (see Moseley et al., 2016, for details). Past DH/DH2 δ¹³C variations have been argued to reflect the extent and density of vegetation in the recharge zones of AMGFS, such that δ¹³C minima correspond to periods of maximum vegetation (Coplen et al., 1994).

Table 2 Correlation coefficient (r) with the 95 % calibrated confidence intervals (in brackets) for pairs of δ¹⁸O, δ¹³C, and δ²³⁴U_i.

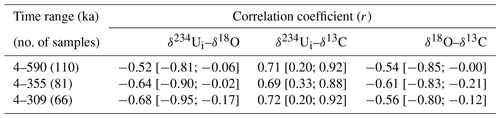
Note that all the 95 % confidence intervals do not cross zero, indicating that all the r values are significant.

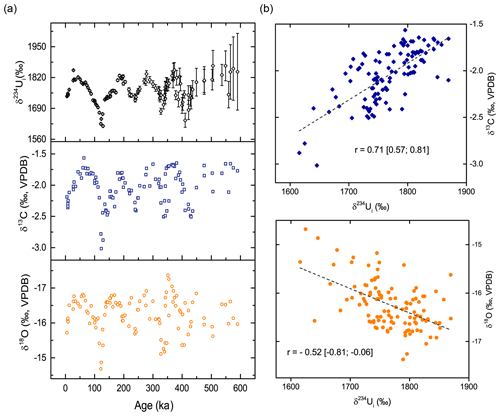
Figure 1 (a) Plots of DH2 ²³⁰Th-derived δ²³⁴U_i, δ¹³C, and δ¹⁸O over the last 590 kyr; (b) scatter plots between DH2 ²³⁰Th-derived δ²³⁴U_i and δ¹³C, and ²³⁰Th-derived δ²³⁴U_i and δ¹⁸O, respectively. Correlation coefficients (r) with 95 % calibrated confidence intervals and fitting curve (dashed lines) are shown.

The linear relationships presented here are consistent with results from Moseley et al. (2016) and Ludwig et al. (1992) in the DH2 and DH caves, respectively. The anti-correlation between δ¹⁸O and δ²³⁴U_i is consistent with the interpretation presented in Wendt et al. (2020) such that periods of increased regional moisture availability (due to cooler, wetter conditions favoring depleted δ¹⁸O values) are associated with increased DH δ²³⁴U_i values. A full list of correlation calculations among δ²³⁴U_i, δ¹⁸O, and δ¹³C is presented in Table 2. The linear relationship between δ¹³C and δ²³⁴U_i is closer than that between δ¹⁸O and δ²³⁴U_i for the same period. This is likely due to the fact that δ¹³C and δ²³⁴U_i are forced by local processes, including changes in vegetation density at the principal recharge zone and groundwater interaction with bedrock in the aquifer. Since changes in the local environmental and hydrological regime are closely interconnected, we expect similar trends in the timing and pattern of δ¹³C and δ²³⁴U_i signals. In contrast, DH/DH2 δ¹⁸O reflects the δ¹⁸O of meteoric precipitation, which is sensitive to regional atmospheric temperatures and changes in moisture source (Winograd et al., 1998; Moseley et al., 2016). Evidence suggests no secular temperature changes in the local aquifer over the last several glacial–interglacial cycles (Kluge et al., 2014); thus, DH/DH2 δ¹⁸O is expected to be minimally influenced by aquifer-related processes. Overall, we expect a greater scatter in the δ¹⁸O vs. δ²³⁴U_i regression due to the compounding forcings that influence δ¹⁸O on a much larger spatial scale.

From Table 2, we can see that the modulus value $\left|r\right|$ for δ¹⁸O and δ²³⁴U_i is greatest in the 4–309 ka dataset, which represents the time span with the highest precision δ²³⁴U_i values. In contrast, the $\left|r\right|$ values for δ¹³C and δ²³⁴U_i are similar regardless of δ²³⁴U_i precision. We therefore explored various time ranges and types of regressions in order to determine the most precise predictor of δ²³⁴U_i based upon δ¹⁸O and/or δ¹³C.

3.1 Regression analysis

We evaluated the linear and polynomial (quadratic and cubic) regression methods primarily by calculating the coefficient of determination (COD), i.e., R². The R² value represents the percentage of variation of the SD δ²³⁴U_i in terms of the total of observed δ²³⁴U_i. To further compare the robustness between different models, we adjusted the R² values from the different numbers of predictors, i.e., the degree of freedom (DF) of the predictors. The adjusted R² (adj. R²) values is shown in Table 3. All models were calculated without considering the analytical uncertainty of δ²³⁴U_i values (see the Supplement for more information).

Table 3 Adjusted R² values for different models with various regression analysis methods.

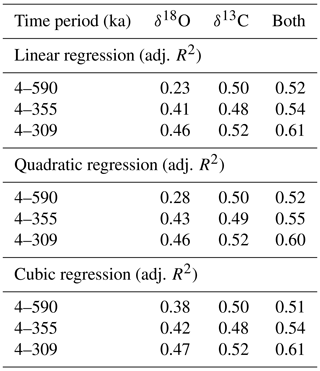
Note that the robustness of the regression model can be evaluated by the coefficient of determination (COD), R², which is defined as R²=1 − (residual sum of squares, RSS)∕(total sum of squares, TSS). Adj. R²=1 − (RSS∕(DF of residual))∕(TSS∕(DF of total predictors)).

Among the various models, multiple linear regression (MLR) for the time period 4–309 ka in terms of both δ¹⁸O and δ¹³C yielded the highest adj. R² value of 0.613 (rounded to 0.61), such that over this time span the model accounts for 61 % of the δ²³⁴U_i variability (Table 3). The corresponding equation is as follows (Table 4):

$$\begin{array}{}\text{(2)}& \mathrm{SD}{\mathit{\delta }}^{\mathrm{234}}{U}_{\mathrm{i}}=\mathrm{1200}-\mathrm{44}\times {\mathit{\delta }}^{\mathrm{18}}\mathrm{O}+\mathrm{86}\times {\mathit{\delta }}^{\mathrm{13}}\mathrm{C}.\end{array}$$

Table 4 A t test table of the multiple linear regression model for 4–309 ka.

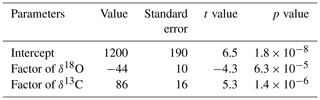
Note that (1) the standard error of fitting parameters was calculated based on the standard deviation of the residual from the model and used only for the t test; (2) a smaller p value represents a decreased likelihood that the parameter is equal to zero.

We then applied statistical methods to test the robustness of the chosen model, starting with the F test. The F value is the ratio of the mean square of the fitted model to the mean square of the residual. A ratio that deviates greatly from 1 indicates that the model differs significantly from the “y = constant” model. The test returned F equal to 52.5, far larger than the critical value of the F test at a significance level of α=0.01 (DF of the numerator is equal to 2; DF of the denominator is equal to 65; F_crit is 4.95), indicating that the model is tenable. Additional confidence in the robustness of the chosen model is derived from the autocorrelation results (see the Supplement).

Second, we performed a t test to check if every term in the MLR for 4–309 ka is significant. The t value is the ratio of the fitted value to its standard error. As shown in the Table 4, all the fitted values (coefficients and intercept) are significant at a significance level of α=0.001. Thus, we conclude the regression model to be robust.

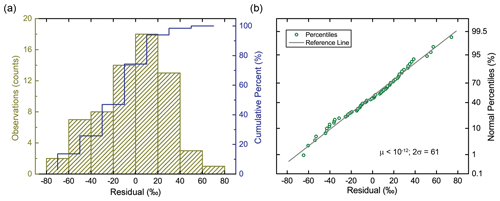
3.2 Residual analysis

We now estimate the uncertainty of the SD δ²³⁴U_i values over the past 309 kyr by analyzing the residuals, which are defined as the differences between the observed and predicted values. Figure 2 reveals that the residuals are approximately normal in distribution. Thus, we conclude that the regression model captures the dominant characteristic of variability in the observed values. The estimate of the residuals yields an uncertainty of ±61 ‰ (95 % confidence interval) with an average of essentially zero (<10⁻¹²). We take the ±61 ‰ value to represent a constant uncertainty for all the SD δ²³⁴U_i values, amounting to a ∼ 40 % reduction in δ²³⁴U_i uncertainties (the original estimate of uncertainty from Ludwig et al. (1992) was 100 ‰). The analytical uncertainty of ²³⁰Th-derived δ²³⁴U_i is combined with (i) uncertainty of measured δ²³⁴U_p, which is incorporated into the ²³⁴U–²³⁸U ages (see the following section), and (ii) the uncertainty of ²³⁰Th ages which is negligible relative to uncertainty of the model over the past 309 kyr (see Tables 1 and S4 for details). Therefore, we do not take this analytical uncertainty into account.

Figure 2 Histogram (a) and normal percentile plot (b) of the residuals. The reference line in panel (b) refers to the line of standard normal distribution.

3.3 ²³⁴U–²³⁸U ages

Using Eqs. (1) and (2), we then calculated the ²³⁴U–²³⁸U disequilibrium ages (denoted in subsequent text as ²³⁴U ages for simplicity) for each data point for which δ²³⁴U_p, δ¹⁸O and δ¹³C are measured. The final uncertainty of ²³⁴U ages comes from two sources: (i) the uncertainty of the model and (ii) the uncertainty in determination of δ²³⁴U_p. Combined, the final uncertainty of ²³⁴U ages before 590 ka is approximately ± 13 kyr (2σ; Table S4), which represents a 35 % improvement relative to previously reported ²³⁴U ages from DH (±20 kyr; Ludwig et al., 1992).

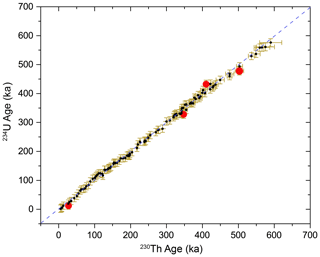
The ²³⁴U and ²³⁰Th ages between 4 and 590 ka are consistent within uncertainties (Fig. 3), with the exception of four ages (out of 110) at 27, 348, 410, and 503 ka. Since uncertainties are reported at the 95 % confidence level, we would expect this number of statistical outliers and conclude that our analysis is overall internally consistent. Alternately, there may be some unknown underlying process not captured by our analysis which may be consistent with the variability of the residuals (see Fig. S3).

Figure 3 Plot of ²³⁴U ages against ²³⁰Th ages between 4 and 590 ka. The 2σ uncertainty shown by brown error bars. The dashed blue line is the 1:1 line, and the red dots refer to four samples inconsistent with this relationship.

3.4 ²³⁴U ages beyond ²³⁰Th–²³⁴U secular equilibrium

The consistency between ²³⁴U and ²³⁰Th ages within the time range of 4–590 ka suggests that it is reasonable to utilize this model to calculate ages that are close to or beyond ²³⁰Th–²³⁴U secular equilibrium in DH/DH2. Using measured δ²³⁴U_p, δ¹⁸O, and δ¹³C values, we calculated 10 ²³⁴U ages for DH2 cave deposits older than 600 ka over the depth of 608 to 652.0 mm (Table 5). The ²³⁴U ages are in stratigraphic order within uncertainty.

Table 5 SD δ²³⁴U_i and calculated ²³⁴U ages from calcite deposited prior to 600 ka and the corresponding depth, δ¹⁸O, δ¹³C, and δ²³⁴U_p values.

4 Discussion

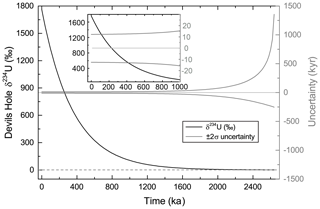
4.1 Uncertainties of ²³⁴U ages

Due to the high initial δ²³⁴U values (1760 ± 61 ‰), DH/DH2 calcite can theoretically be dated up to 2.5 Ma, assuming that measured δ²³⁴U_p values have about 1 ‰ absolute uncertainty. By including all the uncertainty described above, we obtain the following age uncertainty (2σ): ∼ 13 kyr uncertainty for a sample <500 ka, 16 kyr at 1.0 Ma, 26 kyr at 1.5 Ma, 70 kyr at 2.0 Ma, and 290 kyr at 2.5 Ma. The rapid increase in uncertainty after 2.5 Ma (Fig. 4) is due to the fact that ≥ 10 half-lives of the ²³⁴U will have elapsed and the δ²³⁴U_p values increasingly approach the uncertainty of their measurement.

Figure 4 Evolution of δ²³⁴U (black line) and corresponding uncertainties of ²³⁴U ages (grey lines) with time. The insert plot shows the δ²³⁴U evolution during the period of 0–1 Ma. The dashed grey line indicates where δ²³⁴U is 0.

4.2 Timing and rate of calcite deposition

Figure 5 shows an OxCal-derived age model with 95 % confidence intervals plotted over depth using all ²³⁴U ages with their 2σ uncertainties. Locations of folia and a growth hiatus are highlighted. Two lines of evidence suggest that the resulting time series is reasonable. Firstly, the average growth rate during the whole period is at 0.9 ± 0.3 mm kyr⁻¹ (1σ uncertainty; Fig. 6), which is consistent with growth rates reported by Moseley et al. (2016). Secondly, all ²³⁴U ages are in stratigraphic order within uncertainties and fall within the 95 % confidence interval of our age model, implying no major outliers.

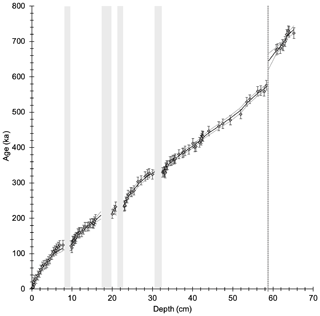
Figure 5 ²³⁴U ages (diamonds) and associated 2σ uncertainties along the length of the core penetrating the calcite crust. OxCal age model (black line) and 95 % confidence limits (grey lines) were derived from ²³⁴U ages. Locations of folia (grey bars) and a growth hiatus (dashed black line) are indicated.

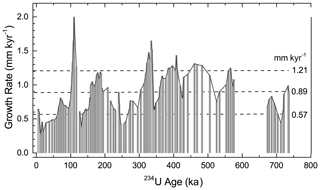
Figure 6 Growth rate of DH2 mammillary calcite based on the OxCal age model (Fig. 5). The dashed lines indicate the average value and 1 standard deviation above and below the average.

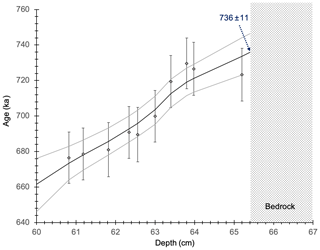
Previous investigations revealed that the DH2 cave opened to the surface at approximately 4 ka (Moseley et al., 2016), likely due to surface collapse processes (Riggs et al., 1994). The timing at which the main subsurface fissure opened, however, remains largely unknown. By ²³⁴U dating, the oldest calcite in our studied core (at the calcite–bedrock boundary), we can determine the earliest-possible timing at which the DH2 fissure existed (without which calcite cannot precipitate). ²³⁴U ages in the last 170 mm of the core are in stratigraphic order within uncertainties (Fig. 7), yet due to the slight scatter of ages we utilize the OxCal age model to extrapolate the age at the calcite–bedrock boundary. In doing so, we determine the earliest calcite in this core (+1.8 m r.m.w.t.) to 736 ± 11 ka (Fig. 7).

The onset of calcite deposition in the DH2 cave is in agreement with the recent geologic history of this region. The orientation of DH and DH2 is in accordance with the principal northwest-southeast stress direction in this part of the Great Basin that has prevailed over the last 5 Myr (Carr, 1974), suggesting that one or both fissures formed after 5 Ma. Abundant calcareous and siliceous spring and marsh deposits in Ash Meadows and the Amargosa Desert of Pliocene age (2.1 to 3.2 Ma; Hay et al., 1986) and groundwater-deposited calcite veins in alluvium and colluvium of Pleistocene age (500 to 900 ka; Winograd and Szabo, 1988) indicate that groundwater in the discharge zone of AMGFS has been continuously supersaturated with respect to calcite for at least the last 3 Myr. Our results, which suggest that the DH2 fissure opened no later than 736 ka, are therefore in agreement with the modern understanding of the AMGFS' geological history.

Figure 7 OxCal-derived age model (black line), 95 % confidence limits (grey lines), and ²³⁴U ages (diamonds) with 2σ uncertainties for the lowest 17 cm of the core. The time series indicates that the initiation of calcite growth in DH2 occurred at 736±11 ka.

5 Conclusions

We have developed a novel method to determine the δ²³⁴U_i values in DH/DH2 calcite. We established a robust multiple linear regression model between δ²³⁴U_i, δ¹⁸O, and δ¹³C values of DH2 calcite deposited between 4 and 309 ka. We applied this model to estimate the δ²³⁴U_i of DH2 calcite using the respective δ¹⁸O and δ¹³C values. We refer to the statically derived initial values as SD δ²³⁴U_i. Uncertainty associated with SD δ²³⁴U_i is ±61 ‰, thereby improving precision by 40 % relative to Ludwig et al. (1992). We then calculated 120 ²³⁴U ages by determining the δ²³⁴U_p and SD δ²³⁴U_i at each age location. Average relative ²³⁴U age uncertainties are 2 %. The concordance between the ²³⁴U and the ²³⁰Th ages younger than 600 ka indicates that the DH2 calcite behaves as a closed system. Overall, 10 of the 120 ²³⁴U ages are located in the oldest portion of the studied DH2 calcite core and range from 676 to 730 ka. Thus, the ²³⁴U ages allow us to extend the DH2 chronology beyond the limits of ²³⁰Th dating (>600 ka). Using our time series, we determined that calcite at the base of the studied core was deposited at 736 ± 11 ka. We argue that this age marks the earliest possible time at which the DH2 fissure existed.