the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
On the viability of detrital biotite Rb–Sr geochronology
Brendan Dyck
Sudip Shrestha
Mark Button
Yani Najman
Re-examination of International Ocean Discovery Program (IODP) sediment samples collected from the Bay of Bengal via laser ablation inductively coupled plasma mass spectrometry (LA-ICP-MS) Rb–Sr geochronology demonstrates the viability of the biotite Rb–Sr system for use as a detrital chronometer. The age population defined by the Rb–Sr dates essentially reproduces that previously published for detrital dates. The effect of unknown/assumed initial on the calculated population can be ameliorated by filtering for higher ratios. Such filtering, however, could introduce bias toward more radiogenic populations, especially in younger material that has not had time to accumulate radiogenic product (e.g. limiting the effect of initial to ∼ <5 % requires filtering of >500 at 250 Ma and >50 at 2500 Ma). Finally, Ti-in-biotite temperatures calculated based on element concentration data collected during LA-ICP-MS overlap with those calculated for the same material based on electron probe microanalyzer data, demonstrating the potential for in situ biotite petrochronology based on the Rb–Sr system.
- Article
(4036 KB) - Full-text XML
-
Supplement
(994 KB) - BibTeX
- EndNote
Detrital geochronology is a commonly used approach to assess a wide variety of geological questions. For example, detrital zircon can provide information about the maximum depositional age for a sedimentary unit, likely sediment sources, and timescales of exhumation and sediment transport (e.g. Gehrels, 2014; Thomas, 2011; Malusà and Fitzgerald, 2020). Moreover, detrital zircon chemistry can provide additional insight into the nature of the source rocks, such as crystallization depth and degree of fractional crystallization (e.g. Stevenson and Patchett, 1990; Iizuka et al., 2010; Howard et al., 2009; Mueller et al., 2008). Detrital geochronology (or thermochronology) of mineral phases dated via radio decay systems that may record cooling rather than crystallization, such as on mica or fission track and U–Th–He dating of U-bearing minerals, can be used to quantify rates of exhumation and/or burial in active orogenic systems (e.g. Ruiz et al., 2004; Najman et al., 1997, 2001; Reiners et al., 2005).
Critical to detrital geochronology, in all forms, is analyzing sufficient material to characterize the statistical variation in the age data. Prior to the development of spot geochronology analytical techniques, analyzing enough material (e.g. Vermeesch, 2004) to characterize a specimen was time-consuming and expensive. The proliferation of geochronology based on laser ablation inductively coupled plasma mass spectrometry (LA-ICP-MS) has enabled the rapid acquisition of large datasets. While this is especially true for detrital U–Pb zircon geochronology, limitations still exist for other methods. For example, LA-ICP-MS geochronology still requires irradiation of samples prior to analysis, which increases the expense and time it takes to generate data.
The development of in situ beta decay geochronology techniques (e.g. Zack and Hogmalm, 2016; Simpson et al., 2021) now allows additional detrital geochronometer options, with the critical caveat that these are typically isochron-based methods. As such, quantifying an initial isotope composition can be an integral part of calculating a date. In the absence of a measured cogenetic non-radiogenic phase to constrain that intercept, multiple radiogenic data points, which typically have varying initial isotopic reservoirs, can be regressed to define a date. Such isochrons (regressions) rely on all analyses comprising a single closed isotopic system, which is incompatible with detrital geochronology. It is possible, however, to assume an initial intercept for isochron-based data and calculate two-point regressions through that intercept and each data point to calculate a spot date. For both Rb–Sr and Lu–Hf, the possible/expected terrestrial initial ratios typically span a rather narrow range of values (e.g. 0.699–0.780 and 0.281–0.283; Rösel and Zack, 2022; Fisher and Vervoort, 2018). Moreover, the more radiogenic the spot analyses are, the less control the initial ratio exerts on the final two-point isochron date. This dependence is demonstrated in Larson et al. (2023a), who show that correcting Rb–Sr data for common 87Sr based on the current , which effectively mimics the result of a two-point isochron through 0.71, effectively reproduces the isochron regression dates for samples with high . The coincidence of the isochron and spot dates derived independently of the measured initial indicates that detrital Rb–Sr geochronology may be a viable alternative or addition to detrital geochronology (e.g. Crossingham et al., 2024), eliminating the potentially time-consuming step of irradiation and facilitating increased numbers of analyses.
This study presents the results of in situ Rb–Sr analysis of biotite mica grains picked from sand samples collected from the Bay of Bengal that have either previously been dated via detrital geochronology or are directly adjacent to dated samples (see Najman et al., 2019). The potential viability of Rb–Sr as a detrital chronometer is compared against the published data. Moreover, the derivation of additional information (i.e. Ti-in-biotite temperature) from the mica grain via LA-ICP-MS is also investigated to determine if it can be used to help further quantify source characteristics.
To test the viability of detrital biotite Rb–Sr geochronology, four samples (1450-24-25F, 1450-100-104-108F, 1451-47-49F, and 1451-86F), collected from Late Miocene to Middle or Late Pleistocene sediments during the Bengal Fan International Ocean Discovery Program (IODP) Expedition 354, were examined. For simplicity, the sample names have been shortened here to 25F, 108F, 49F, and 86F, respectively. These same samples, or closely adjacent ones, have been previously investigated for detrital white mica , zircon fission track, apatite U–Pb, and/or rutile U–Pb geochronology (Najman et al., 2019). Given the propensity for biotite (sensu lato) to be more radiogenic than white mica (e.g. Fournier et al., 2016) and the sensitivity of low radiogenic material to the initial value of an isochron, only biotite was targeted in this study. The biotite grains were either manually picked from sediment separates (see Najman et al., 2019) and mounted in epoxy, or the sediments were poured directly into an epoxy mount. Grains were not mounted with a preferred orientation, resulting in a semi-random c-axis orientation (the natural shape of a mica lath favours a c axis normal to the mounting surface). Mixed c-axis orientations may help avoid less optimal signal stability ablating parallel to the mica c axis (Rösel and Zack, 2022), which may affect the final Rb–Sr date calculated (Lloyd et al., 2023). After polishing, targets were verified (i.e. the presence of K and Fe and the lack of visible inclusions) via micro-XRF elemental mapping of each mount prior to analysis.
2.1 Rb–Sr geochronology
Rb–Sr geochronology was carried out via laser ablation inductively coupled plasma tandem mass spectrometry following the methods initially set out in Zack and Hogmalm (2016) and Hogmalm et al. (2017). Analyses were carried out in the Fipke Laboratory for Trace Element Research (FiLTER) at the University of British Columbia, Okanagan (UBCO), using a laser (ESL NWR193) with a TwoVol3 ablation cell paired with an Agilent 8900 triple quadrupole (QQQ) ICP-MS instrument as described in Larson et al. (2023a, b). A circular laser spot with a diameter of 65 µm, an approximate pit depth of ∼ 10–15 µm, a fluence of ∼ 3 J cm−2, and a repetition rate of 5 Hz was used for all materials. Analyses of the glass reference material NIST SRM 610 (Jochum et al., 2011) were carried out using both 60 and 30 µm diameter laser spots to ensure the analyses were measured in both pulse and analogue detector modes for cross-calibration (e.g. Zack and Hogmalm, 2016; Glorie et al., 2024). Instrument drift was corrected, and down-hole fractionation was minimized (e.g. Glorie et al., 2023), based on analyses of NIST SRM 610 using an in-house data reduction scheme (DRS; Larson, 2024) developed for iolite v.4.X (Paton et al., 2011) based on the freely available “U–Pb Python Example.py” DRS (Petrus, 2022), following the approach and error propagation detailed in Redaa et al. (2021), and using a covariance matrix to calculate error correlation. Matrix fractionation effects on were corrected based on repeated analyses of Mica 1O (phlogopite – 986 ± 5 Ma; Camacho et al., 2020) and verified based on the analyses of GA-1550 (Mt Dromedary biotite – 98.7 ± 1.9 Ma, Li et al., 2008). During run 1 (108F and 47-49F), GA-1550 returned an isochron date of 99.6 ± 3.5 Ma (mean squared weighted deviation (MSWD) = 1.9, , initial = 0.7049 ± 0.0017). During run 2 (25F and 86F), GA-1550 returned an isochron date of 98.1 ± 2.3 Ma (MSWD = 0.93, , initial = 0.7049 ± 0.0017), while an additional in-house reference material, Mica 1B (phlogopite – 990 ± 6 Ma; Camacho et al., 2012), returned an isochron date of 997 ± 6 Ma (MSWD = 3.7, , initial = 0.7035 ± 0.0005). Full Rb–Sr data are provided in Tables S1 and S2.
2.2 Ti-in-biotite thermometry
In addition to Rb–Sr isotopes, Ti, Mg, and Fe concentrations were measured for each analytical spot via LA-ICP-MS with dwell times of 1, 0.5, and 1 ms, respectively. Concentrations were normalized to repeated measurements of the NIST SRM 610 glass reference material (Jochum et al., 2011) assuming stoichiometric Si (16.36 weight (wt.) % Si or 35 wt % SiO2), typical of metamorphic biotite from greenschist through granulite facies (e.g. Dyck et al., 2021). Titanium concentrations (ppm) were converted to molar-weight-per-oxide TiO2 equivalents and then normalized to calculated Si content based on an assumed 5.4 atoms per formula unit (a.p.f.u.) Si per 22 O as detailed in Eq. (1):
where CTi is the concentration of Ti in ppm, WTTiO2 is the weight proportion of Ti in TiO2, MTiO2 is the molar weight per oxide, and ASi is the molar weight per cation Si assuming 35 wt % SiO2. Ti-in-biotite temperatures were calculated using the equation of Henry et al. (2005), which requires Ti a.p.f.u and Mg# (Mg(Mg + Fe)) for each analysis. The values for Mg# were calculated using parts-per-million (ppm) concentrations of Fe and Mg. The 1σ uncertainty of the Ti-in-biotite temperatures is <24 °C at 480 °C decreasing to 12 °C at 800 °C (Henry et al., 2005).
To verify the LA-ICP-MS-derived Ti-in-biotite temperatures, the chemistries of the same mica grains were analyzed using the CAMECA SXFiveFE electron probe microanalyzer (EPMA), also housed in the FiLTER facility. Quantitative spot analyses were carried out with an acceleration voltage of 15 kV, a regulated beam current of 20 nA, and a spot size of 5 µm. Elemental x-ray data were collected using a dwell time of 30 s on peak and 15 s on background and were calibrated to the known composition of synthetic and natural mineral reference standards from Micro-Analysis Consultants Ltd. The standards used for calibration were spessartine for Si and Mn, titanite for Ti, almandine for Al and Fe, wollastonite for Ca, albite for Na, diopside for Mg, orthoclase for K, and apatite for P. The crystals used were LTAP for Si and Al; LPET for Ti, Ca, K, and P; LLIF for Fe and Mn; and TAP for Na, Mg. The EPMA data were converted to atoms-per-formula-unit biotite on the basis of 22 oxygen whereby
Given that the biotite analyzed was collected as detritus from the Bengal Fan and given the tendency of biotite to weather (e.g. Wilson, 2004), alteration was expected. To avoid the most altered material, EPMA data were filtered for totals >88 wt % and K concentrations >1.1 a.p.f.u. Plotting K a.p.f.u against Mg# or calculated temperature shows that analyses with K a.p.f.u. >1.1 rarely form outliers (Fig. 3). While it is recognized that an a.p.f.u of 1.1 K is significantly lower than that expected of unaltered biotite, K is expected to leave the mineral via hydrated cation exchange as part of the initial weathering stage/vermiculitization (Price and Velbel, 2014; Gilkes and Suddhiprakarn, 1979). In contrast, Fe, Mg, and Ti are relatively immobile until more advanced alteration of biotite to goethite or kaolinite (Gilkes and Suddhiprakarn, 1979). Exchange of hydrated cations with interlayer K will result in lower-oxide EPMA wt % totals, which, upon normalization (for a biotite with an XMg of 0.44), increases the temperature calculated using the Ti-in-biotite thermometer by ∼ 2.2 °C per 1 wt % oxide deficit. The sensitivity of Ti-in-biotite temperatures to EPMA oxide wt % totals, using the Henry et al. (2005) calibration, is shown in Fig. S1. To illustrate the effect of weathering on our data we plot all analyses, coloured by oxide wt % totals, in Fig. 3a and b. In general, filtering analyses with K concentrations >1.1 a.p.f.u rather than filtering solely on oxide wt % totals is the more robust approach to removing outliers with anomalously low Mg# (e.g. <0.15) and Ti-in-biotite temperatures (e.g. <400 °C). Full EPMA data are provided in Table S3.
3.1 Rb–Sr geochronology
All Rb–Sr results were filtered for (>3), Fe + Mg (between 15 % and 26 wt %), and Ti (>0.1 a.p.f.u) to avoid spurious analyses. Of the 137 spot analyses of biotite from specimen 25F, 132 remained after filtering. The data spread between isochrons at 45 and 8 Ma and define an over-dispersed (MSWD = 12.9) ca. 13 Ma isochron (Fig. 1a). Similarly, 138 spots in biotite from 108F yield 102 viable analyses that spread between 5 and 30 Ma isochrons. The data define an over-dispersed regression (MSWD = 5.5) at ca. 14 Ma (Fig. 1b). Of 104 analyses in biotite separated from 49F, 96 spread between isochrons at 10 and 30 Ma, defining an over-dispersed (MSWD = 3.0) isochron at ca. 16 Ma (Fig. 1c). Finally, 113 of 117 biotite analyses of material from 86F spread between isochrons at 37 and 11 Ma and comprise an over-dispersed (MSWD = 6.88) regression at ca. 15 Ma (Fig. 1d).
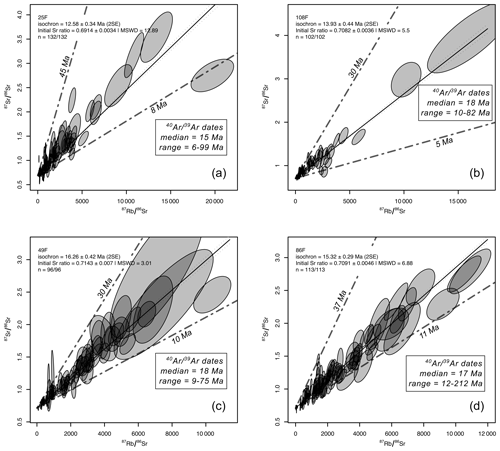
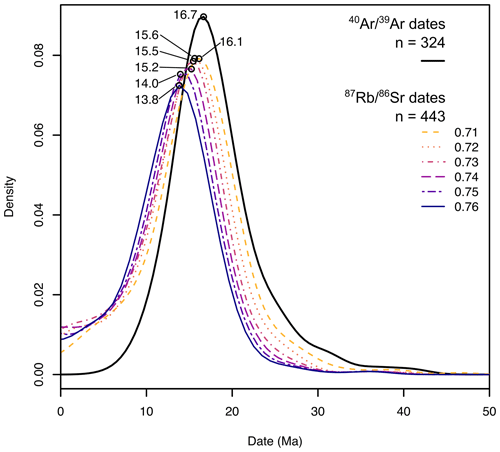
Figure 1 versus isochron plots of data collected from each sample investigated (a–d). Dashed lines denote the approximate envelope of each dataset with corresponding dates as marked. dates quoted are from Najman et al. (2019) and correspond to data from samples 1450-38-40F, 1450-98F, 1451-31-33-37F, and 1451-86F for 25F, 108F, 49F, and 86F, respectively.
For each specimen, spot dates were calculated as two-point dates based on a regression between each analysis and a specified initial value (see Tables S4–S7). The initial values used (0.71, 0.72, 0.73, 0.74, 0.75, and 0.76) cover the range of expected values for most plutonic and metamorphic sources (Rösel and Zack, 2022). The dates calculated for each specimen are depicted in Fig. 2 as kernel density estimations (KDEs; bandwidth = 3). In general, the KDEs have a single peak for >0 Ma dates (if a spot analysis has an < the initial , a negative date will be calculated, a situation exacerbated in young material that has not had time to accumulate radiogenic 87Sr; see Tables S4–S7). The KDE peaks for each specimen generally increase in width, decrease in height, and move to slightly younger positions with two-point dates calculated with progressively higher initial (Fig. 2).
3.2 Ti-in-biotite thermometry
Ti-in-biotite temperatures calculated via LA-ICP-MS data generally range between ∼ 650 and 725 °C for most samples (Fig. 3b, c). The SiO2 content used in the calculations has little effect on temperature. Increasing the SiO2 from 35 wt % to 40 wt % results in only an ∼ 5 °C temperature change (Fig. S2), well within the expected uncertainty of the method (Henry et al., 2005). While the precision of Ti data generated by LA-ICP-MS is lower than EPMA data, the second- and third-quartile temperatures overlap (within uncertainty) with those calculated using EPMA data for each specimen (Fig. 3c).
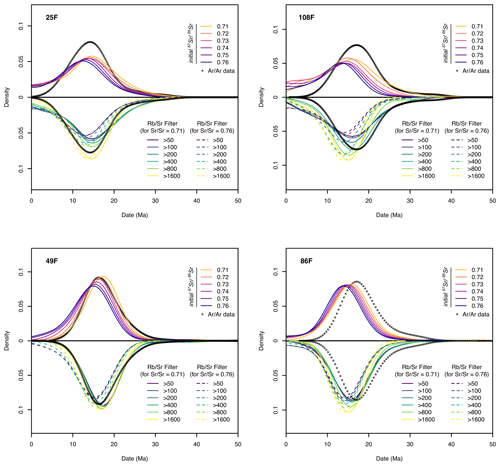
Figure 2Kernel density estimation (KDE) plots of Rb–Sr data from samples analyzed and of the same or spatially adjacent samples. The kernel bandwidth was 3 Ma for all plots. Each diagram shows two different datasets. The data plotted above the median line include white mica dates and unfiltered Rb–Sr two-point isochron dates based on initial as marked. Dates were calculated using IsoplotR (Vermeesch, 2018). The data plotted below the median line represent the results of applying different filters, as noted.
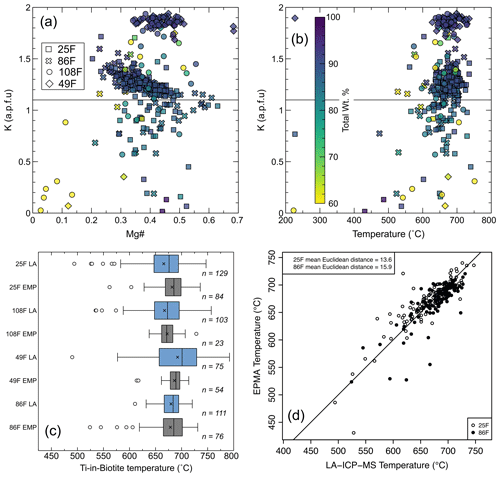
Figure 3(a) Plot of K atoms per formula unit (a.p.f.u; based on 22O) as calculated from electron probe microanalyzer (EPMA) data versus Mg# (,Mg/(Fe + Mg)). A horizontal line is drawn at K a.p.f.u = 1.1. (b) Plot of K a.p.f.u. versus derived Ti-in-biotite temperature. A horizontal line is drawn at K a.p.f.u = 1.1. (c) Box-and-whisker plots of calculated Ti-in-biotite temperatures calculated for each sample via EPMA data (grey fill) and laser ablation inductively coupled plasma mass spectrometry (LA-ICP-MS) data (blue fill). (d) Plot of EPMA versus LA-ICP-MS temperatures for adjacent spot analyses on the same grains in samples 25F and 86F. Calculated mean Euclidean distances between the EPMA versus LA-ICP-MS data points for each sample are shown.
4.1 Effect of initial
As with any isochron method, the value of the intercept can have a significant impact on the results when calculating two-point isochron Rb–Sr dates. That effect, however, is less significant with older material (higher radiogenic Sr) and more radiogenic analyses. As shown in Fig. 4, the effect of initial intercept selection can be demonstrated by generating three artificial datasets with one analysis every 500 increments between 10 and 4510. One dataset defines a 25 Ma isochron, one defines a 250 Ma isochron, and one defines a 2500 Ma isochron, each with an initial of 0.70. Two-point spot Rb–Sr dates were calculated for each data point within each model for different initial ranging from 0.71 to 0.79, and the percent of absolute deviation in two-point isochron date for each modelled point from the “known” date (i.e. 25, 250, or 2500 Ma) was quantified (Fig. 4). Plotting the % change in two-point isochron date versus demonstrates that young, low- material is most affected by changing the initial . Moreover, the plot further demonstrates that for high (∼ >2500), even in young material, the typical difference in initial encountered in most crustal rocks (i.e. 0.70–0.76; Rösel and Zack, 2022) will have ∼ <5 % effect on the date calculated (Fig. 4). For older material, the cut-offs to minimize the effect of initial on dates (i.e. <5 %) drop significantly (i.e. ∼ > = 500 at 250 Ma and ∼ > = 50 at 2500 Ma; Fig. 4).
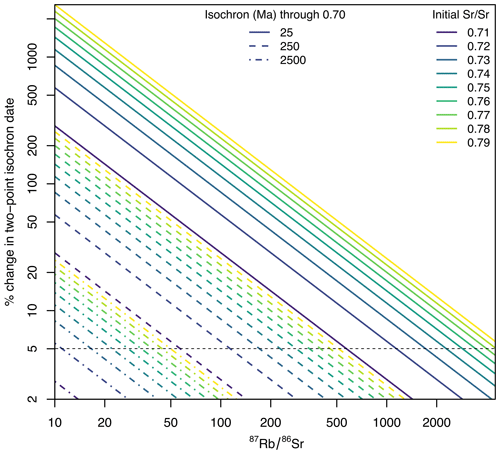
Figure 4Plot of modelled data demonstrating the related effects of initial on calculated two-point isochron dates as a function of . See text for discussion.
The effect of initial relative to can be further investigated using the real-world data presented herein. Filtering the two-point isochron dates calculated based on demonstrates that the position of the main population of the data remains relatively invariant for different but that the half-width decreases and the density of the main population increases with higher cut-offs (bottom curves Fig. 2). These results indicate that filtering detrital data by may help ameliorate the complication of unknown initial values, though it should be noted that doing so would introduce bias toward more radiogenic populations and, as such, should not be done in isolation.
4.2 Comparison with detrital geochronology
Najman et al. (2019) presented the results of various detrital geochronology methods employed on the samples examined in the current study and/or other proximal samples. These methods include geochronology on white mica. White mica was targeted in that study both because of the common problem of excess Ar associated with biotite (Stübner et al., 2017; Larson et al., 2023a) in the Himalayan system from which these samples were collected (i.e. Himalayan detritus shed into the Bay of Bengal) and because of the resilience of white mica, relative to biotite, to weathering (Wilson, 2004). Given the differences in child product retention between white mica geochronology and biotite Rb–Sr geochronology, it may not be expected that the data from the two systems would overlap. White mica has an estimated nominal closure temperature of ∼ 425–400 °C for Ar diffusion (100 µm radius grain, 10°C Ma−1 cooling rate, 5–10 kbar; Harrison et al., 2009), whereas closure to diffusion of Sr out of biotite is more varied, with estimates ranging from ∼ 300 °C (Jager et al., 1967; Armstrong et al., 1966) to ∼ 400 °C (Verschure et al., 1980; Del Moro et al., 1982) or even in excess of 400 °C depending on the specifics of the mineralogy and chemistries of the samples (Jenkin et al., 1995, 2001). This variability in chronometer “closure temperatures” (e.g. Dodson, 1973) may be reflected in variable offsets between the Rb–Sr and dates (Fig. 2).
The various two-point isochron Rb–Sr dates calculated for 108F and 86F define density peaks with a slightly younger (∼ 1 Ma) offset than the dates (initial = 0.71), whereas for 49F and 25F two-point isochron dates essentially reproduce the density peak of the dates (Fig. 2). Overall, the total Rb–Sr dataset, regardless of initial used, defines a similar dominant population of Early to Middle Miocene age (Fig. 5) to that noted by Najman et al. (2019). That peak was interpreted to demonstrate rapid exhumation of the eastern and central Himalaya with an ∼ <4 Myr lag time between exhumation through mica closure to child product diffusion and sedimentation (Najman et al., 2019). Given the similarities between the datasets, the detrital Rb–Sr geochronology would have led to the same conclusions as the data generated by Najman et al. (2019).
4.3 Ti-in-biotite thermometry
Comparison of EPMA and LA-ICP-MS thermometry results demonstrates that LA-ICP-MS data can yield results comparable with traditional methods (Fig. 3). The temperatures calculated for the spot data are consistent with derivation from amphibolite facies metamorphic rocks or from associated leucogranites (e.g. Waters, 2019), which dominate the inferred exhuming Himalayan midcrustal source (Najman et al., 2019). The temperatures also broadly overlap with Zr-in-rutile temperature derived from detrital rutile from the same samples (∼ 650–780 °C; Najman et al., 2019). Direct comparison of LA-ICP-MS- and EPMA-derived temperatures for the same grains from 25F and 86F defines mean Euclidean distances of 13.6 and 15.9 °C, respectively (Fig. 3d). Because this approximately 15 °C uncertainty likely reflects the analytical precision of LA-ICP-MS rather than being solely due to the uncertainties stemming from natural variations in biotite chemistry or the thermometer calibration, it should be regarded as additive to the ±12–24 °C 1σ uncertainty of Henry et al. (2005). The precision on the Ti-in-biotite temperature estimates, whether EPMA- or LA-ICP-MS-derived, does not facilitate quantifying a change across the sampled strata, as data from all samples overlap (Fig. 3c).
The viability of quantifying Ti-in-biotite temperatures via LA-ICP-MS allows each Rb–Sr spot analyzed to be associated with a unique temperature. This kind of petrochronologic association opens the possibility of many different types of studies, not unlike the linking of chemistry to spot dates did for U(–Th)–Pb geochronology in the early 2000s (e.g. Foster et al., 2004; Gibson et al., 2004; Rubatto, 2002).
LA-ICP-MS Rb–Sr geochronology appears to be a viable method to efficiently generate detrital biotite geochronological datasets. The effect of unknown initial values can be mitigated for young (Cenozoic) material by filtering for significantly radiogenic analyses ( >2500), though such filtering may introduce bias. Filtering can be less aggressive for older material (i.e. >500 at 250 Ma) in which significant radiogenic child product has accumulated. Finally, the benefits of biotite Rb–Sr geochronology can be further extended by calculating a Ti-in-biotite temperature for each spot. Such information may allow the identification of multiple sources in detrital samples with complex provenance.
All data related to this study are available on the Open Science Framework website: https://osf.io/vgjh6/?view_only=52b27e0d000c4f2ea6b9ab665744e43c (OSF, 2024).
The supplement related to this article is available online at: https://doi.org/10.5194/gchron-6-303-2024-supplement.
KPL: conceptualization, funding acquisition, methodology, investigation, visualization, and writing (original draft preparation). BD: methodology, investigation, and writing (review and editing). SS: investigation and writing (review and editing). MB: investigation and writing (review and editing). YN: resources and writing (review and editing).
The contact author has declared that none of the authors has any competing interests.
Publisher’s note: Copernicus Publications remains neutral with regard to jurisdictional claims made in the text, published maps, institutional affiliations, or any other geographical representation in this paper. While Copernicus Publications makes every effort to include appropriate place names, the final responsibility lies with the authors.
Stijn Glorie and Hugo Olierook are thanked for their constructive reviews. Axel Schmitt is thanked for editorial handling.
This research has been supported by the Natural Sciences and Engineering Research Council of Canada (grant no. RGPIN-2021-02501).
This paper was edited by Axel Schmitt and reviewed by Stijn Glorie and Hugo Olierook.
Armstrong, R. L., Jäger, E., and Eberhardt, P.: A comparison of K-Ar and Rb-Sr ages on Alpine biotites, Earth Planet. Sc. Lett., 1, 13–19, 1966.
Camacho, A., Lee, J. K. W., Fitz Gerald, J. D., Zhao, J., Abdu, Y. A., Jenkins, D. M., Hawthorne, F. C., Kyser, T. K., Creaser, R. A., Armstrong, R., and Heaman, L. W.: Planar defects as Ar traps in trioctahedral micas: A mechanism for increased Ar retentivity in phlogopite, Earth Planet. Sc. Lett., 341–344, 255–267, 2012.
Camacho, A., Lee, J. K. W., Zhao, J., Abdu, Y. A., Fayek, M., and Creaser, R. A.: A test of the interlayer ionic porosity model as a measure of argon diffusivity in trioctahedral micas, Geochim. Cosmochim. Ac., 288, 341–368, 2020.
Crossingham, T., Sobczak, K., La Croix, A. D., Esterle, J., Dalton, H., and Hayes, P.: Detrital or reset? dating of mica from the Lower Jurassic Precipice Sandstone and Evergreen Formation in the Surat Basin, Aust. J. Earth Sci., 71, 585–599, https://doi.org/10.1080/08120099.2024.2319105, 2024.
Del Moro, A., Puxeddu, M., di Brozolo, F. R., and Villa, I. M.: Rb-Sr and K-Ar ages on minerals at temperatures of 300°–400° C from deep wells in the Larderello geothermal field (Italy), Contrib. Mineral. Petrol., 81, 340–349, 1982.
Dodson, M.: Closure temperature in cooling geochronological and petrological systems, Contrib. Mineral. Petrol., 40, 259–274, 1973.
Dyck, B., Goddard, R. M., Wallis, D., Hansen, L. N., and Martel, E.: Metamorphic evolution of the Great Slave Lake shear zone, J. Metamorph. Geol., 39, 567–590, 2021.
Fisher, C. M. and Vervoort, J. D.: Using the magmatic record to constrain the growth of continental crust—The Eoarchean zircon Hf record of Greenland, Earth Planet. Sc. Lett., 488, 79–91, 2018.
Foster, G. L., Parrish, R. R., Horstwood, M. S. A., Chenery, S., Pyle, J., and Gibson, H. D.: The generation of prograde P–T–t points and paths; a textural, compositional, and chronological study of metamorphic monazite, Earth Planet. Sc. Lett., 228, 125–142, https://doi.org/10.1016/j.epsl.2004.09.024, 2004.
Fournier, H. W., Camacho, A., and Lee, J. K. W.: High-strain deformation and fluid infiltration diachronism of the middle crust: New Devonian–Permian Alice Springs ages (365–290 Ma) of shear zones in the Strangways Metamorphic Complex, Central Australia, Chem. Geol., 443, 39–53, 2016.
Gehrels, G.: Detrital Zircon U-Pb Geochronology Applied to Tectonics, Annu. Rev. Earth Planet. Sci., 42, 127–149, 2014.
Gibson, H. D., Carr, S. D., Brown, R. L., and Hamilton, M. A.: Correlations between chemical and age domains in monazite, and metamorphic reactions involving major pelitic phases: an integration of ID-TIMS and SHRIMP geochronology with Y–Th–U X-ray mapping, Chem. Geol., 211, 237–260, 2004.
Gilkes, R. J. and Suddhiprakarn, A.: Biotite alteration in deeply weathered granite. I. Morphological, mineralogical, and chemical properties, Clays Clay Miner., 27, 349–360, 1979.
Glorie, S., Gilbert, S. E., Hand, M., and Lloyd, J. C.: Calibration methods for laser ablation Rb–Sr geochronology: comparisons and recommendation based on NIST glass and natural reference materials, Geochronology, 6, 21–36, https://doi.org/10.5194/gchron-6-21-2024, 2024.
Glorie, S., Simpson, A., Gilbert, S. E., Hand, M., and Müller, A. B.: Testing the reproducibility of in situ Lu Hf dating using Lu-rich garnet from the Tørdal pegmatites, southern Norway, Chem. Geol., 653, 122038, 2024.
Harrison, T. M., Célérier, J., Aikman, A. B., Hermann, J., and Heizler, M. T.: Diffusion of 40Ar in muscovite, Geochim. Cosmochim. Ac., 73, 1039–1051, 2009.
Henry, D. J., Guidotti, C. V., and Thomson, J. A.: The Ti-saturation surface for low-to-medium pressure metapelitic biotites: Implications for geothermometry and Ti-substitution mechanisms, Am. Mineral., 90, 316–328, 2005.
Hogmalm, J. K., Zack, T., -O. Karlsson, A. K., Sjöqvist, A. S. L., and Garbe-Schönberg, D.: In situ Rb–Sr and K–Ca dating by LA-ICP-MS/MS: an evaluation of N2O and SF6 as reaction gases, J. Anal. At. Spectrom., 32, 305–313, 2017.
Howard, K. E., Hand, M., Barovich, K. M., Reid, A., Wade, B. P., and Belousova, E. A.: Detrital zircon ages: Improving interpretation via Nd and Hf isotopic data, Chem. Geol., 262, 277–292, 2009.
Iizuka, T., Komiya, T., Rino, S., Maruyama, S., and Hirata, T.: Detrital zircon evidence for Hf isotopic evolution of granitoid crust and continental growth, Geochim. Cosmochim. Ac., 74, 2450–2472, 2010.
Jager, E., Niggli, E., and Wenk, E.: Rb-Sr Altersbestimmungen an Glimmern der Zentralalpen, Kummerly & Frey, 1967.
Jenkin, G. R. T., Rogers, G., Fallick, A. E., and Farrow, C. M.: Rb-Sr closure temperatures in bi-mineralic rocks: a mode effect and test for different diffusion models, Chem. Geol., 122, 227–240, 1995.
Jenkin, G. R. T., Ellam, R. M., Rogers, G., and Stuart, F. M.: An investigation of closure temperature of the biotite Rb-Sr system: The importance of cation exchange, Geochim. Cosmochim. Ac., 65, 1141–1160, 2001.
Jochum, K. P., Weis, U., Stoll, B., Kuzmin, D., Yang, Q., Raczek, I., Jacob, D. E., Stracke, A., Birbaum, K., Frick, D. A., Günther, D., and Enzweiler, J.: Determination of Reference Values for NIST SRM 610-617 Glasses Following ISO Guidelines, Geostandard. Geoanal. Res., 35, 397–429, 2011.
Larson, K. P.: LA-ICP-MS RbSr Data Reduction Scheme, OSF [code], https://doi.org/10.17605/OSF.IO/VJAF2, 2024.
Larson, K. P., Button, M., Shrestha, S., and Camacho, A.: A comparison of and dates: Evaluating the problem of excess 40Ar in Himalayan mica, Earth Planet. Sc. Lett., 609, 118058, https://doi.org/10.1016/j.epsl.2023.118058, 2023a.
Larson, K. P., Dyck, B., Faisal, S., Cottle, J. M., and Searle, M.: Metamorphic and intrusive history of the Hindu Raj region, northern Pakistan, Geol. Mag., 160, 1376–1394, 2023b.
Li, Q.-L., Chen, F., Li, X.-H., Wang, F., and He, H.-Y.: Single grain Rb-Sr isotopic analysis of GA-1550 biotite, LP-6 biotite and Bern-4M muscovite 40Ar-39Ar dating standards, Geochem. J., 42, 263–271, 2008.
Lloyd, J. C., Gilbert, S., Glorie, S., Hand, M., and Spandler, C.: In-situ Rb–Sr dating of micas: the devil is in the details, in: Goldschmidt 2023 Conference, Lyon, France, 9–14 July 2023, 2023.
Malusà, M. G. and Fitzgerald, P. G.: The geologic interpretation of the detrital thermochronology record within a stratigraphic framework, with examples from the European Alps, Taiwan and the Himalayas, Earth-Sci. Rev., 201, 103074, https://doi.org/10.1016/j.earscirev.2019.103074, 2020.
Mueller, P. A., Kamenov, G. D., Heatherington, A. L., and Richards, J.: Crustal Evolution in the Southern Appalachian Orogen: Evidence from Hf Isotopes in Detrital Zircons, J. Geol., 116, 414–422, 2008.
Najman, Y., Pringle, M. S., Johnson, M., Robertson, A. H. F., and Wijbrans, J. R.: Laser dating of single detrital muscovite grains from early foreland-basin sedimentary deposits in India: Implications for early Himalayan evolution, Geology, 25, 535–538, 1997.
Najman, Y., Pringle, M. S., Godin, L., and Oliver, G.: Dating of the oldest continental sediments from the Himalayan foreland basin, Nature, 410, 194–197, 2001.
Najman, Y., Mark, C., Barfod, D. N., Carter, A., Parrish, R., Chew, D., and Gemignani, L.: Spatial and temporal trends in exhumation of the Eastern Himalaya and syntaxis as determined from a multitechnique detrital thermochronological study of the Bengal Fan, Geol. Soc. Am. Bull., 131, 1607–1622, 2019.
OSF: On the viability of detrital Rb-Sr geochronology, OSF [data set], https://osf.io/vgjh6/?view_only=52b27e0d000c4f2ea6b9ab665744e43c, last access: 13 May 2024.
Paton, C., Hellstrom, J., Paul, B., Woodhead, J., and Hergt, J.: Iolite: Freeware for the visualisation and processing of mass spectrometric data, J. Anal. At. Spectrom., 26, 2508–2512, 2011.
Petrus, J.: U-Pb Python Example, GitHub [code], https://github.com/iolite-LA-ICP-MS/iolite4-python-examples/blob/master/drs (last access: 25 June 2024), 2022.
Price, J. R. and Velbel, M. A.: Rates of biotite weathering, and clay mineral transformation and neoformation, determined from watershed geochemical mass-balance methods for the coweeta hydrologic laboratory, southern Blue Ridge mountains, North Carolina, USA, Aquat. Geochem., 20, 203–224, 2014.
Redaa, A., Farkaš, J., Gilbert, S., Collins, A. S., Wade, B., Löhr, S., Zack, T., and Garbe-Schönberg, D.: Assessment of elemental fractionation and matrix effects during in situ Rb–Sr dating of phlogopite by LA-ICP-MS/MS: implications for the accuracy and precision of mineral ages, J. Anal. At. Spectrom., 36, 322–344, 2021.
Reiners, P. W., Ehlers, T. A., and Zeitler, P. K.: 1. Past, present, and future of thermochronology, in: Low-Temperature Thermochronology:, edited by: Reiners, P. W. and Ehlers, T. A., De Gruyter, Berlin, Boston, 1–18, https://doi.org/10.1515/9781501509575-003, 2005.
Rösel, D. and Zack, T.: LA-ICP-MS/MS single-spot Rb-Sr dating, Geostand. Geoanal. Res., 46, 143–168, 2022.
Rubatto, D.: Zircon trace element geochemistry: partitioning with garnet and the link between U–Pb ages and metamorphism, Chem. Geol., 184, 123–138, 2002.
Ruiz, G. M. H., Seward, D., and Winkler, W.: Detrital thermochronology – a new perspective on hinterland tectonics, an example from the Andean Amazon Basin, Ecuador, Basin Res., 16, 413–430, 2004.
Simpson, A., Gilbert, S., Tamblyn, R., Hand, M., Spandler, C., Gillespie, J., Nixon, A., and Glorie, S.: In-situ Lu–Hf geochronology of garnet, apatite and xenotime by LA ICP MS/MS, Chem. Geol., 577, 120299, https://doi.org/10.1016/j.chemgeo.2021.120299, 2021.
Stevenson, R. K. and Patchett, P. J.: Implications for the evolution of continental crust from Hf isotope systematics of Archean detrital zircons, Geochim. Cosmochim. Ac., 54, 1683–1697, 1990.
Stübner, K., Warren, C., Ratschbacher, L., Sperner, B., Kleeberg, R., Pfänder, J., and Grujic, D.: Anomalously old biotite ages in the NW Himalaya, Lithosphere, 9, 366–383, 2017.
Thomas, W. A.: Detrital-zircon geochronology and sedimentary provenance, Lithosphere, 3, 304–308, 2011.
Vermeesch, P.: How many grains are needed for a provenance study?, Earth Planet. Sc. Lett., 224, 441–451, 2004.
Vermeesch, P.: IsoplotR: A free and open toolbox for geochronology, Geosci. Front., 9, 1479–1493, 2018.
Verschure, R. H., Andriessen, P. A. M., Boelrijk, N. A. I. M., Hebeda, E. H., Maijer, C., Priem, H. N. A., and Verdurmen, E. A. T.: On the thermal stability of Rb-Sr and K-Ar biotite systems: Evidence from coexisting Sveconorwegian (ca 870 Ma) and Caledonian (ca 400 Ma) biotites in SW Norway, Contrib. Mineral. Petrol., 74, 245–252, 1980.
Waters, D. J.: Metamorphic constraints on the tectonic evolution of the High Himalaya in Nepal: the art of the possible, Geological Society, London, Special Publications, 483, 325–375, 2019.
Wilson, M. J.: Weathering of the primary rock-forming minerals: processes, products and rates, Clay Miner., 39, 233–266, 2004.
Zack, T. and Hogmalm, K. J.: Laser ablation dating by online chemical separation of Rb and Sr in an oxygen-filled reaction cell, Chem. Geol., 437, 120–133, 2016.