Short communication: Nanoscale heterogeneity of U and Pb in baddeleyite from atom probe tomography – ²³⁸U series alpha recoil effects and U atom clustering

Atom probe tomography (APT) of ²³⁸U and ²⁰⁶Pb has been applied to baddeleyite crystals from the Hart Dolerite (1791±1 Ma) and the Great Dyke of Mauritania (2732±2 Ma) in an effort to constrain the average nuclear recoil distance of ²³⁸U series daughter nuclei and correct alpha-recoil-induced Pb loss on U–Pb ages from small baddeleyite crystals. The Hart Dolerite sample showed no variations in Pb concentrations near the edge and is interpreted to represent a cleaved surface instead of the original crystal surface. The Great Dyke sample shows U zoning, and the associated ²⁰⁶Pb zoning is affected by alpha recoil, apparently adjacent to a natural grain surface. This sample also shows primary clusters of U atoms at a scale of 10 nm that contain about 40 % of the total U. ${}^{\mathrm{207}}\mathrm{Pb}{/}^{\mathrm{206}}\mathrm{Pb}$ nanogeochronology suggests that the clusters are primary in origin; however, they are too small to constrain alpha recoil distance beyond a few nanometres. To constrain alpha recoil distance, a forward-modelling approach is presented where ²⁰⁶Pb redistribution functions were determined for a range of possible recoil distances. Synthetic ${}^{\mathrm{206}}\mathrm{Pb}{/}^{\mathrm{238}}\mathrm{U}$ profiles were determined from the convolution of the observed U profile with the redistribution functions for different alpha recoil distances. These were compared to the observed ${}^{\mathrm{206}}\mathrm{Pb}{/}^{\mathrm{238}}\mathrm{U}$ profile to determine the recoil distance that gives the best fit. The observed U zoning was extrapolated to account for the full range of possible alpha recoil redistribution effects, which is larger than the 40 by 400 nm size of the APT field of view. Any reasonable extrapolation constrains the average alpha recoil distance to over 70 nm, which is much larger than previous estimates using other methods. This could be because recoil distances can be highly anisotropic within small crystal samples or because laterally non-uniform U zoning was a factor that modified the recoiled Pb distribution. APT is a potentially useful approach for determining average alpha recoil distance but requires sampling of primary smooth crystal faces with demonstrably uniform zones.

1 Introduction

Atom probe tomography (APT) can be used to directly observe the distribution of individual atoms of elements in a mineral crystal lattice (Reddy et al., 2020). APT has been applied to baddeleyite in previous studies, mostly using the baddeleyite mineral standard Phalaborwa (Reinhard et al., 2018) and/or crystals that underwent shock metamorphism (White et al., 2018b, 2017). One germane finding of these studies is that while major elements are homogeneously distributed at the atomic level in baddeleyite, radiogenic Pb and incompatible trace elements (Si, Mg, Al, Yb, and Fe) can be heterogeneously distributed in nanoscale domains (White et al., 2017, 2018a, b). The nanoscale U distribution in Phalaborwa baddeleyite crystals was also shown to be variable with localized zonation, and heating baddeleyite to temperatures up to 500 °C does not seem to affect that distribution (White et al., 2017).

Baddeleyite (monoclinic ZrO₂) is a common geochronometer in silica-undersaturated rocks that can be dated with <0.1 % age precision using isotope dilution thermal ionization mass spectrometry (ID-TIMS). Like zircon (tetragonal ZrSiO₄), U is incorporated into its crystallizing lattice, but Pb is not. Unlike zircon, radiation damage from the decay of U and its radioactive daughters has minimal effect in the form of Pb loss (Rioux et al., 2010; Lumpkin, 1999). However, minor discordance (<3 %) between the ${}^{\mathrm{206}}\mathrm{Pb}{/}^{\mathrm{238}}\mathrm{U}$ and ${}^{\mathrm{207}}\mathrm{Pb}{/}^{\mathrm{235}}\mathrm{U}$ systems is common in baddeleyite of all ages, outside of uncertainties in U decay constants (Rioux et al., 2010; Schoene et al., 2006). Apparent daughter loss in younger samples (<400 Ma for ID-TIMS), where age interpretations must be based on ${}^{\mathrm{206}}\mathrm{Pb}{/}^{\mathrm{238}}\mathrm{U}$ ratios rather than ${}^{\mathrm{207}}\mathrm{Pb}{/}^{\mathrm{206}}\mathrm{Pb}$ ratios, is manifested as younger ${}^{\mathrm{206}}\mathrm{Pb}{/}^{\mathrm{238}}\mathrm{U}$ dates, but data are still generally concordant due to relatively large ${}^{\mathrm{207}}\mathrm{Pb}{/}^{\mathrm{235}}\mathrm{U}$ uncertainties. This is because at young ages discordia lines become subparallel to the concordia curve.

Baddeleyite does not appear to be as susceptible to low-temperature alteration as radiation-damaged zircon, although it can break down to polycrystalline zircon with accompanying Pb loss during metamorphism (Davidson and van Breemen, 1988). This may be because its chemical stability is due to its composition, whereas that of zircon is due to its structure, which is disrupted by radiation damage. Therefore, pre-treatment methods such as air abrasion (Krogh, 1982) or annealing and HF-leaching (“chemical abrasion”; Mattinson, 2005) processes that are designed to remove alteration and are frequently employed to mitigate Pb loss in zircon are generally unnecessary or ineffective (e.g. Rioux et al., 2010). Various mechanisms have been proposed for observed discordance in baddeleyite. They include microcrystalline or cryptocrystalline zircon overgrowths, which are susceptible to extensive Pb loss (e.g. Darling et al., 2016; Schmieder et al., 2015); loss of intermediate daughter ²²²Rn through diffusion (Heaman and LeCheminant, 2001); excess intermediate daughters ²³¹Pa (Ivanov et al., 2021; Sun et al., 2020; Amelin and Zaitsev, 2002) and ²³⁰Th (Wu et al., 2015); and daughter loss through alpha recoil (Denyszyn et al., 2009; Davis and Sutcliffe, 1985). In particular, apparent preferential ²⁰⁶Pb loss leading to a biased effect on both ${}^{\mathrm{206}}\mathrm{Pb}{/}^{\mathrm{238}}\mathrm{U}$ and ${}^{\mathrm{207}}\mathrm{Pb}{/}^{\mathrm{206}}\mathrm{Pb}$ ratios has been observed with improved precision on single analyses and has been attributed to excess ²³¹Pa (Ibañez-Mejia and Tissot, 2019) and/or ²²²Rn mobility (Pohlner et al., 2020). An observed relationship between grain size, specifically surface area-to-volume ratio, and degree of ²⁰⁶Pb loss where crystal rims are more strongly affected than cores, implies either fast-pathway and/or volume diffusion of ²²²Rn (Pohlner et al., 2020) or, most likely, alpha recoil as a cause.

Alpha recoil refers to the displacement of daughter radioisotopes as a result of the ejection of an alpha particle from the parent. The resulting lattice damage to the mineral's crystal structure facilitates Pb loss after low-temperature alteration, a well-documented phenomenon in zircon (e.g. Nasdala et al., 2010). Pb and other intermediate daughters in the U decay series can also be directly ejected from the crystal. Recoil distances for single alpha decays have been calculated to range from 20 to 33 nm in zircon (Nasdala et al., 2001), and while the directions of the alpha emission and recoil are random, an average cumulative recoil distance from the eight decays of the ²³⁸U decay series should be about 3 times the average single recoil distance. There are seven decays in the ²³⁵U decay series. Therefore, a zone of U daughter depletion can be expected to make up the outer ca. 50–100 nm of a given zircon crystal (Davis and Davis, 2018), representing a volume in which alpha recoil loss can be significant. Even in zircon crystals that are relatively equant compared to the flat, bladed habit of baddeleyite, and therefore have relatively low surface-area-to-volume ratios, alpha recoil can generate measurable discordance (Romer, 2003). For a crystal of 100 µm in its longest dimension and a 2:1 aspect ratio, this depletion zone can make up ca. 0.3 % of the volume of intact crystals that have not undergone physical or chemical abrasion (Schmieder et al., 2015).

As alpha recoil is a fundamental physical process that must occur with every radioactive decay, determining average alpha recoil distance is important to establish the degree to which discordance in baddeleyite can be attributed to this process. The alpha recoil distance has implications for the minimum useful volume of baddeleyite for geochronology and for the selection of subsamples for spatially detailed analysis (e.g. FIB-TIMS, White et al., 2020) because recoil will redistribute radiogenic Pb from internally zoned U. Accurate knowledge of the recoil distance would allow at least first-order corrections to ID-TIMS $\mathrm{Pb}/\mathrm{U}$ ages based on the dimensions of samples.

Determining alpha recoil distances in baddeleyite from laboratory measurements is challenging. Denyszyn et al. (2009) tested the requisite correlation of grain size and apparent age of baddeleyites on the order of 10 µm thickness and could not resolve any effect on ${}^{\mathrm{206}}\mathrm{Pb}{/}^{\mathrm{238}}\mathrm{U}$ ratios at the scale of typical ID-TIMS U–Pb analyses, suggesting that recoil distances in baddeleyite are shorter than those for zircon. The strongest effects of alpha recoil should be seen at a natural baddeleyite grain surface, where there is a large reduction in U concentration from inside to outside the crystal. Pb concentrations within the crystal, hence ${}^{\mathrm{206}}\mathrm{Pb}{/}^{\mathrm{238}}\mathrm{U}$, should drop by a factor of 2 at the crystal surface (Davis and Davis, 2018). Thus far, the only direct measurement is by Davis and Davis (2018), who used a sensitive high-resolution ion microprobe (SHRIMP II) to create depth profiles of ${}^{\mathrm{206}}\mathrm{Pb}{/}^{\mathrm{238}}\mathrm{U}$ ratios away from natural crystal surfaces in baddeleyite. Measurements were made on a total of five spots from two natural grain surfaces from the 2059 Ma Phalaborwa carbonatite (Heaman, 2009). They obtained a value of 24±7 nm for the average recoil distance, which is similar to that calculated for zircon. The SHRIMP measurements were difficult because of the strong dependence of $\mathrm{Pb}/\mathrm{U}$ biases on the condition of the sputtered surface in secondary ion mass spectrometry. As the hole deepens, the bias must be corrected by comparison with results from analysis of a polished crystal surface of a grain from the same sample. U concentrations were also found to drop off within grains near natural surfaces during some analyses, which was unexpected, but the average recoil distance was found to be about the same whether or not this was taken as an artefact.

Alpha recoil results in a distribution of radiogenic Pb atoms that differs from the U distribution in having smaller concentration gradients. As mentioned, the largest U gradient should be encountered immediately at the crystal surface (Davis and Davis, 2018). The degree of broadening of the Pb distribution away from a natural surface can be calculated for an assumed average alpha recoil distance and compared to the measured profile, thus providing a way to potentially constrain its value as was done by Davis and Davis (2018). However, APT should be less affected by biases in $\mathrm{U}/\mathrm{Pb}$ measurements with depth of analysis and can also be used in the absence of a natural surface provided there is sufficient U variation due to zoning. We therefore applied APT to two baddeleyite crystals of known age and constructed profiles of U and radiogenic Pb distribution in order to constrain average alpha recoil distance in baddeleyite for the ²³⁸U decay chain and to study the distribution of U atoms.

2 Analytical and modelling methods

2.1 Sample preparation

Samples were selected based on identification of well-defined crystal faces, concordant U–Pb analyses, and relatively old age and high U content to ensure measurable abundances of U and radiogenic Pb. Baddeleyite crystals were chosen from the Hart Dolerite (our specimen M2, ${}^{\mathrm{207}}\mathrm{Pb}{/}^{\mathrm{206}}\mathrm{Pb}$ age of 1790.5±1.4 Ma; Ramsay et al., 2019, their sample GS11043-1) and the Great Dyke of Mauritania (M5, upper-intercept age of 2733±2 Ma; Tait et al., 2013, their sample GTD-8). All age errors are quoted at 95 % confidence.

Figure 1 Scanning electron photomicrographs of the two studied baddeleyite crystals: (a) Hart Dolerite and (b) Great Dyke of Mauritania. Rectangles denote apparent fresh crystal faces. The higher-relief feature is the platinum strip applied to protect the selected region from gallium implantation and to facilitate handling of the selected area after being carved out by the focussed ion beam.

Sample preparation followed methods as in Thompson et al. (2007) and Rickard et al. (2020). Both baddeleyite grains were picked and placed on individual scanning electron microscope (SEM) aluminium stubs covered by carbon tape (Fig. 1a and b). The stubs were sputter-coated with an approximately 200 nm thick layer of Cr to serve both as a conductive layer and as a cap protecting the surface of the baddeleyite grains. Atom probe specimens were prepared from the Cr-coated grain with a Ga⁺ TESCAN LYRA3 focused ion beam (FIB) at the Microscopy and Microanalysis Facility (MMF), Curtin University. A Pt layer was sublimated along the surface of the crystal in order to protect the region of interest from Ga implantation, and Pt sublimation was used to fuse the needle-shaped specimen to the APT specimen holder. The FIB was operated at an accelerating voltage of 30 kV during the sculpting of the specimens and at 2 kV in the final stage to remove the external layer affected by the high-energy Ga beam. During the final stage of polishing, some Cr cap was intentionally left at the apex of the specimens to identify the original crystal surfaces (Fig. 2a and b). In the case of sample M2, the Cr cap was deposited oblique to the long axis of the specimen, either due to surface irregularities or the sample not being exactly horizontal at the time of Cr deposition.

Figure 2 Scanning electron photomicrographs of atom probe tomography specimens from (a) sample M2 of the Hart Dolerite sample and (b) M5 of the Great Dyke of Mauritania. The observed crystal surfaces are beneath the Cr cap.

2.2 Atom probe tomography (APT)

APT relies on the field evaporation of ions from a needle-shaped specimen. The original position of the ions in the analyzed volume is given in three dimensions and at sub-nanometre resolution by a position-sensitive detector. The ions are identified by their time of flight and reported on a mass-to-charge ratio spectrum (mass spectrum in Dalton). This study used the Geoscience Atom Probe (Cameca LEAP 4000X HR) at Curtin University. The instrument was operated in laser-assisted mode with a UV (λ=355 nm) laser set at 100 pJ pulse energy and at a repetition rate of 125 kHz. The specimens were maintained at 50 K base temperature in order to inhibit surface diffusion during analysis. In the mass-to-charge ratio spectra, peaks higher than twice the background were identified and ranged for three-dimensional reconstructions using Cameca's APsuite 6.3 software. Voltage evolution reconstructions were performed using a detector efficiency of 0.36, an image compression factor of 1.65, and a k-factor of 3.3. For baddeleyite, the atomic volume was calculated at 0.01133 nm³ per atom, and the electric field was empirically determined at 29.08 V nm (Fougerouse et al., 2022). Tomographic data for one specimen of each grain were successfully acquired, with 62 million ions for specimen M5 (Great Dyke of Mauritania) and 65 million ions for specimen M2 (Hart Dolerite). Depth concentration profiles were generated for a 5 nm bin size and exclude the Cr cap.

The U and Pb isotopic compositions were quantified from the atom probe data using a narrow range (0.1 Da) for each isotopic ionic species. Uranium was spread over several ionic species with the dominant ²³⁸UO${}_{\mathrm{2}}^{++}$ (135 Da) but also ²³⁸UO${}_{\mathrm{2}}^{+}$ (270 Da) and ²³⁸UO${}^{+++}$ (84.7 Da). No peaks were visible above background for any species of ²³⁵U. Lead was present as ²⁰⁶Pb${}^{++}$ and ²⁰⁷Pb${}^{++}$ (103 and 103.5 Da, respectively). The local background signal was measured by selecting a wide “peak-free” region (0.5 to 1 Da) in proximity to each ionic species and normalized to the width of the species range (0.1 Da). Uncertainties were estimated at 1σ using counting statistics and propagating background corrections adapting protocols previously defined for baddeleyite, zircon, and monazite (Fougerouse et al., 2018; White et al., 2017; Peterman et al., 2016). A summary of APT results is presented in the supplementary data repository, File 1, operating parameters are in File 6, and raw .RHIT files are in the supplementary data repository.

2.3 Alpha recoil modelling

Modelling of the ²⁰⁶Pb concentration was carried out based on the observed ²³⁸U distribution and assumed values of R, the average value of the recoil distance for each of the eight alpha emitting nuclides. This was done by calculating an estimation of the redistribution function for a given R value and calculating the convolution of this function with the observed U distribution. As in Davis and Davis (2018), the assumed planar symmetry of the zoned U distribution simplifies the calculations, allowing the results to be expressed as two-dimensional profiles where the redistribution function varies only with distance along the axis, normal to the plane of zoning. Each point source of U atoms generates a uniform radial distribution of Pb atoms around it extending out to 8R. If the sample exhibits planar U zoning, the distribution of recoiled Pb atoms from a single layer of U atoms will be given by the overlap of these spherical distributions. This will produce a zoned Pb distribution that represents a broadening of the U distribution in the z direction, but the distribution of Pb atoms in the z direction will still be the same for any x–y position. The Pb distribution along z can therefore be modelled from any point source of U atoms from a single x1–y1 position on the plane of zoning. The flux of recoiled Pb atoms from any other x–y position onto the z1 vector must be equal to the z component of a recoil from x1–y1 because concentrations remain uniform in the x–y plane. Therefore, it is only necessary to randomize the recoil distance (0 to R) along the z direction for 8 recoils from a population of atoms that occupies a single point on the x–y plane.

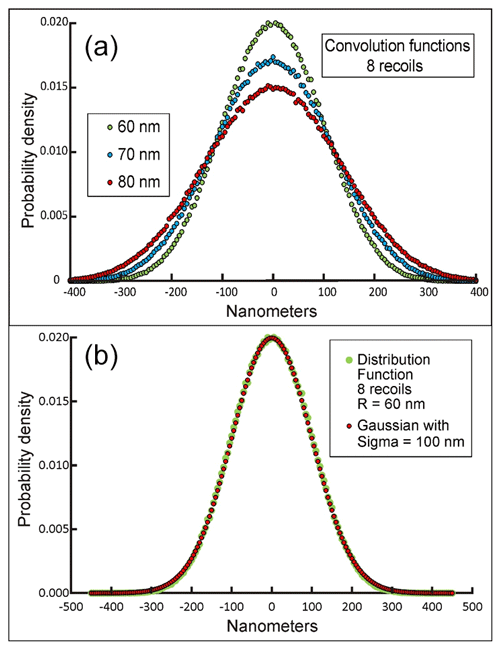
Figure 3 (a) Redistribution curves determined for eight alpha recoils of 1 million atoms with assumed recoil distances (R) of 60, 70, and 80 nm. The curves are normalized to an area of 1. (b) Comparison of redistribution curve for R=60 nm with a Gaussian function with sigma of 100 nm.

This is done for a population of 1 million atoms. The shape of the resultant curve of number of recoiled atoms versus normal distance, when normalized to an area of 1, approximates the redistribution function for eight recoils each with distance R (Fig. 3a). Calculations of redistributed Pb profiles were done using Visual Basic for Applications (VBA) in Excel. See the supplementary data repository, File 2 for examples. This contains software and instructions for repeating the calculations with different values of R.

An average recoil distance is used for simplicity in formulating the problem, but this does not describe the true kinetics of a recoiling nucleus. Each of the eight nuclei in the ²³⁸U chain decay have different energies and thus will have different average recoil distances. Also, recoiled nuclei transfer energy to host atoms by multiple scattering events, which is the source of radiation damage, so their actual paths are complicated and cover a range of values even for the same decay. None of this is relevant to the problem of correcting ${}^{\mathrm{206}}\mathrm{Pb}{/}^{\mathrm{238}}\mathrm{U}$ ages, which requires knowledge of the dimensions of the analyzed crystals and the ²⁰⁶Pb redistribution curve, a function of the average total displacement of a ²⁰⁶Pb daughter atom from its decayed ²³⁸U nucleus. Thus, even if the R value is an average, it is useful for characterizing their overall displacement.

The distribution functions after eight recoils closely approximate a Gaussian curve (Fig. 3b). As shown in the supplementary data repository, File 2 “Recoil 40 nm” sheet, the distribution from even three recoils shows the approximate form of a Gaussian. Convergence to a Gaussian shape by recursion of any random process, even one whose distribution is itself non-Gaussian, is predicted by the Central Limit Theorem (Casella and Berger, 2018, p. 236). The 1σ widths of the visually approximated Gaussian curves shown in the supplementary data repository, File 2 are about 1.67R.

The redistribution function expresses the concentration of recoiled Pb atoms from a single layer of U atoms. The recoiled Pb distribution resulting from a U distribution that is zoned in the z direction is given by the convolution of the observed U profile with the above-determined area-normalized redistribution function. The convolution function spreads the content of each bin along z according to the chosen redistribution function, summing the resulting totals in each z bin. This can then be compared to the observed ²⁰⁶Pb distribution. The result gives a theoretical recoiled ²⁰⁶Pb distribution and profile of ${}^{\mathrm{206}}\mathrm{Pb}{/}^{\mathrm{238}}\mathrm{U}$ ratios with the assumed value of R, which can be compared to measured distributions.

Figure 4 (a) Hypothetical Gaussian-shaped ²³⁸U distribution peak on a constant background representing a present-day concentration of 0.005 %. Assuming an age such that half the original ²³⁸U has decayed into ²⁰⁶Pb (4468 Ma), the resulting radiogenic ²⁰⁶Pb distribution after eight alpha recoils is shown for an assumed average recoil distance of 40 nm. (b) Resulting ${}^{\mathrm{206}}\mathrm{Pb}{/}^{\mathrm{238}}\mathrm{U}$ ratio profile.

Figure 4 and the supplementary data repository, File 2 “Fig. 4” sheet illustrate the result of eight alpha recoils with R of 40 nm on the Pb distribution from decay of a hypothetical Gaussian-shaped U concentration with sigma of 60 nm, which is of similar scale to the peak above background U in the sample. For simplicity, it is assumed that the amount of ²³⁸U at present is equal to the amount of ²⁰⁶Pb produced. As demonstrated in the supplementary data repository, File 2 “G-G Convol” sheet, convolution of a Gaussian curve produces a wider Gaussian curve. The ${}^{\mathrm{206}}\mathrm{Pb}{/}^{\mathrm{238}}\mathrm{U}$ profile shows roughly symmetrical peaks on each side of the U peak, where excess ²⁰⁶Pb has been projected from adjacent high-U levels on each side of the peak onto part of the tail, raising the ratio from 1, while within the U peak the ratios are less than 1.

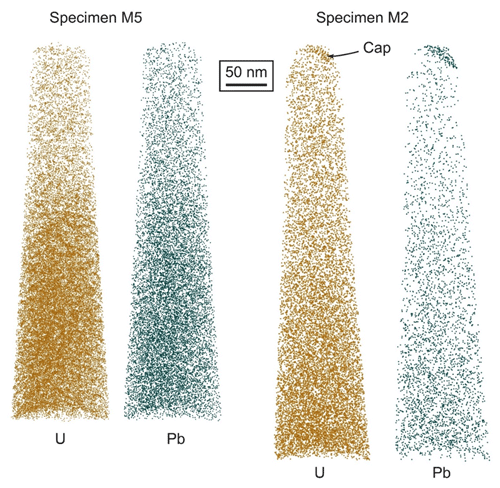
Figure 5 Distribution of ²³⁸U and ²⁰⁶Pb atoms in specimens M5 and M2 from atom probe tomography. The observed crystal surfaces, indicated in both samples as beginning under the Cr caps seen in Fig. 2, are at the upper parts of the distributions (<0 nm distance). Some of the Cr cap of specimen M2 is still present here. See video files in the supplementary data repository for 3D visualization of the clustered U and Pb atoms in specimen M5.

3 Results

3.1 U and ${}^{\mathrm{206}}\mathrm{Pb}{/}^{\mathrm{238}}\mathrm{U}$ zoning from APT

The U concentration in specimen M5 (Mauritania) is higher than in specimen M2 (Hart) with an average U of 288 ppma (parts per million atomic) for M5 and 23 ppma for M2. In specimen M5, the distribution of U shows a gradient of concentration from low U content near the presumed surface of the grain and higher content inwards (Fig. 5), varying from approximately (within ca. 10 %) 150 to 650 ppma over the measured 500 nm.

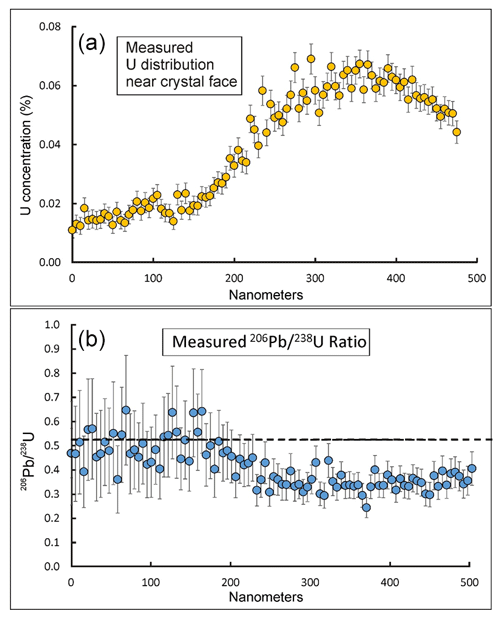
Figure 6 (a) Measured ²³⁸U percentage concentration along the z axis of sample M5. (b) Measured ${}^{\mathrm{206}}\mathrm{Pb}{/}^{\mathrm{238}}\mathrm{U}$ ratio along the z axis of sample M5. The dotted line represents the equilibrium ${}^{\mathrm{206}}\mathrm{Pb}{/}^{\mathrm{238}}\mathrm{U}$ value for the age of the sample. Error bars represent 2σ. The lowering of ${}^{\mathrm{206}}\mathrm{Pb}{/}^{\mathrm{238}}\mathrm{U}$ ratio over the U peak below the equilibrium value is expected due to redistribution of Pb by recoil, but this should produce ratios next to the peak that are above the equilibrium value unless 0 nm represents a crystal boundary.

The Cr cap coating preserved at the tips of the atom probe specimens confirms the apparent position of the crystal surfaces (Fig. 2). Surprisingly, profiles of background-corrected abundances of Pb for each crystal (Fig. 5) do not show the expected sudden drop-off of Pb from alpha recoil ejection in the outermost 10–50 nm as seen in previous SHRIMP measurements (Davis and Davis, 2018). For specimen M5, the abundances of Pb and U are non-uniform, with a zone of relative enrichment in the 200–400 nm depth range (Figs. 5 and 6), which is interpreted to represent growth zoning of U but for Pb may in part reflect alpha recoil. Sample M2 shows a uniform U concentration (Fig. 5) and is thus of no use for constraining alpha recoil distance beyond the conclusion that if it were sampled at a crystal boundary the recoil distance must be very short (<5 nm). If the recoil distance was greater, the step in U concentration along the axis of sample M5 (Fig. 6a) should result in Pb concentration effects dependent on alpha recoil distance. M5 also has more radiogenic Pb because it is the oldest and has the higher U concentration, which makes parent-to-daughter ratios easier to measure.

The sampled surfaces of the baddeleyite crystals appeared to be natural crystal surfaces based on visual inspection under SEM imaging and the absence of obvious fracturing. In the Davis and Davis (2018) study, one out of the three studied grains also did not show decreasing Pb near the crystal boundary, and it was concluded that this surface may have been a recently exposed cleavage plane, which may also be the case for sample M2.

3.2 Alpha recoil modelling results from U zoning

The measured U concentration and ${}^{\mathrm{206}}\mathrm{Pb}{/}^{\mathrm{238}}\mathrm{U}$ ratio profiles in M5 are shown in Fig. 6. These are calculated from the number of ²³⁸U and ²⁰⁶Pb atoms in a volume bin perpendicular to the long axis of the specimen (Fig. 5), where zero is at the top edge of the specimen (0 nm), assumed to be a crystal boundary. The measured age of M5 corresponds to an equilibrium radiogenic ${}^{\mathrm{206}}\mathrm{Pb}{/}^{\mathrm{238}}\mathrm{U}$ ratio of 0.53. The measured ${}^{\mathrm{206}}\mathrm{Pb}{/}^{\mathrm{238}}\mathrm{U}$ profile shown in Fig. 6b is roughly constant and close to the equilibrium value for distances of about 1 to 150 nm, which corresponds to the low-U zone. It then drops to a fairly constant value that is notably lower than equilibrium over the peak of the high-U zone. If the recoil distance were very small (less than a few nanometres), Pb would not be significantly displaced from U and one would expect the ${}^{\mathrm{206}}\mathrm{Pb}{/}^{\mathrm{238}}\mathrm{U}$ profile to be constant, independent of the U concentration, which is not the case. If the recoil distance were very large, Pb would be redistributed approximately independent of the U profile and should have a constant composition. In this case, the ratio profile would be proportional to the inverse of the U concentration. The measured profile does show that the ${}^{\mathrm{206}}\mathrm{Pb}{/}^{\mathrm{238}}\mathrm{U}$ ratios are low where the U concentration is high and high where it is low, but the U concentrations differ by a factor of >3, whereas the ratio levels differ by about 1.5. Therefore, alpha recoil must have significantly modified the daughter Pb distribution.

The measured U profile is not wide enough to avoid effects of recoil beyond its measured range. It is therefore necessary to extrapolate the profile above and below. Given that there are two unknowns, one of which is an array, the determination of R will not be unique, but it may be possible to constrain it by reasonable assumptions and examining how different U distributions affect the shape of the ratio profile.

The shape of the measured ${}^{\mathrm{206}}\mathrm{Pb}{/}^{\mathrm{238}}\mathrm{U}$ profile constrains likely adjacent U concentrations and alpha recoil distance. It is remarkable that the ${}^{\mathrm{206}}\mathrm{Pb}{/}^{\mathrm{238}}\mathrm{U}$ ratio over the low-U part of the zone is fairly constant and close to the equilibrium ratio because modelling from a U peak on a constant background (Fig. 4b) predicts that the ratio should be higher than the equilibrium value. The fact that the ratio adjacent to the U peak is not higher than equilibrium requires that the U concentrations to the left (at negative distances) be close to zero. This suggests that the crystal face was a natural grain surface as assumed. Therefore, we assign a value of zero for U concentrations at negative distance. Another qualitative deduction is that the average alpha recoil distance must be quite large (>40 nm) to explain the relatively flat ${}^{\mathrm{206}}\mathrm{Pb}{/}^{\mathrm{238}}\mathrm{U}$ profile over the U peak and that it is so far below the equilibrium ratio.

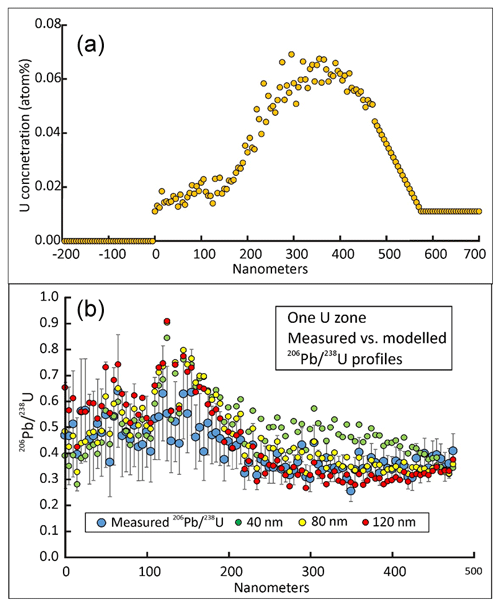
Figure 7 (a) Measured (0–475 nm) and linearly extrapolated U distribution. A distance of 0 nm represents the crystal face. (b) Measured versus modelled ${}^{\mathrm{206}}\mathrm{Pb}{/}^{\mathrm{238}}\mathrm{U}$ profiles for different assumed values of average recoil distance across the measured distance range, assuming the U concentration profile shown in (a). Error bars on measured data represent 2σ. Note that the range of (b) covers the range of measurements in (a).

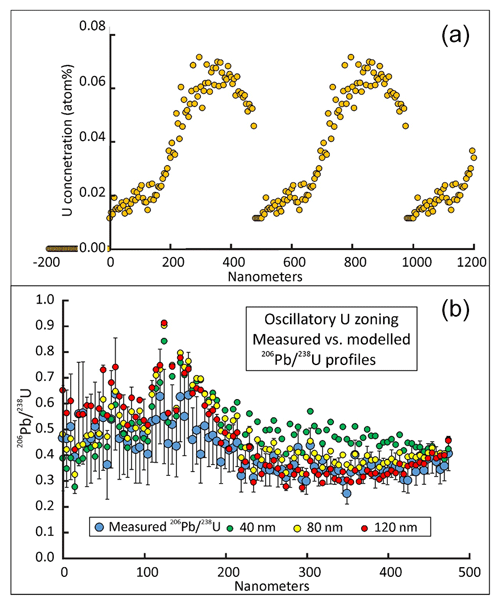
Figure 8 (a) Measured (0–475 nm) and extrapolated U distribution assuming oscillatory zoning. A distance of 0 nm represents the crystal face. (b) Measured versus modelled ${}^{\mathrm{206}}\mathrm{Pb}{/}^{\mathrm{238}}\mathrm{U}$ profiles for an assumed value of average recoil distance of 40 nm assuming the oscillatory high-U zones shown in (a). Error bars on measured data represent 2σ. Note that the range of (b) covers the range of measurements in (a).

Assuming that the U concentrations at <0 nm are zero and those at >475 nm are projected linearly downward to the value at 0 nm, which is then kept constant (Fig. 7a), results in the models shown in Fig. 7b for assumed values of 40, 80, and 120 nm for the average distance of a single recoil. The distance that gives the best fit is about 80 nm based on visual assessment and the mean square of weighted deviation (MSWD) as described below. This model visually fits the ratio profile at the start (0–50 nm) and over most of the U peak (200–450 nm) quite well but shows excess Pb near the foot of the U peak (50–150 nm). Lowering the ratio for this part of the profile would require a larger recoil distance to smooth the distribution of Pb recoiled from the right, but this would cause more Pb to recoil out of the peak region, dropping its modelled ${}^{\mathrm{206}}\mathrm{Pb}{/}^{\mathrm{238}}\mathrm{U}$ ratio below the measured value, as shown in Fig. 7b for the 120 nm model. This might be offset by assuming a high-U region to the right of the measured profile. The simplest assumption is that of oscillatory zoning, as shown in Fig. 8a. However, the main effect of zoning is to slightly raise the ratios on the right end of the ratio profile (Fig. 8b).

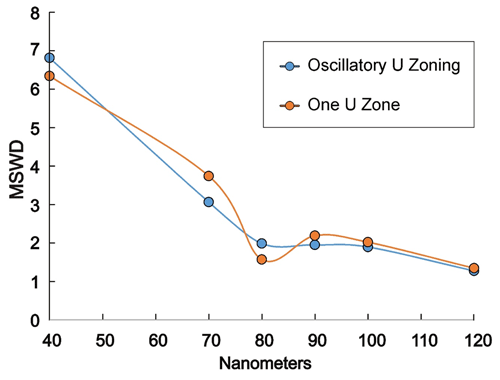
Figure 9 Mean square of weighted deviation (MSWD) for modelled versus measured ${}^{\mathrm{206}}\mathrm{Pb}{/}^{\mathrm{238}}\mathrm{U}$ profiles as a function of the assumed average recoil distance, assuming the oscillatory zoned U distribution shown in Fig. 8a and the single U zone shown in Fig. 7a. The curves fitting the datasets are spline fits determined by Excel.

The modelled distributions straddle the observed scatter over the observed U peak but tend to be above the measured ratio distribution over the low-U part. The MSWD (Fig. 9) shows local minima of about 1.5–2.0 at 80 nm for both U extrapolations but continues to drop at higher recoil values up to 120 nm probably because the profile flattens over the low-U section and provides a better fit. Modelled ratios for higher recoil distances fall below the measured profile over the U peak because of greater Pb loss due to recoil. Pb can be added by making the extrapolated zones higher in U, but this will increase the curvature of the profile unless recoil distance is made even larger. The results of modelling on these and a number of other extrapolated profiles are shown in the supplementary data repository, File 2. In order to reduce MSWD down to 1.5, the average recoil distance must be assumed to be about 80 nm. It would be unrealistic for us to assign an error to this estimate. It might be assigned on the basis of the measurement errors in the data but it would be dependent on only one extrapolation model. The problem is that we cannot evaluate all possible models for extrapolation of the U distribution beyond the range of measurement but within the range of alpha recoil effects. It might be possible after considering a larger range of models, but we have not carried this further since any estimate from the present data is unlikely to be accurate for reasons discussed below.

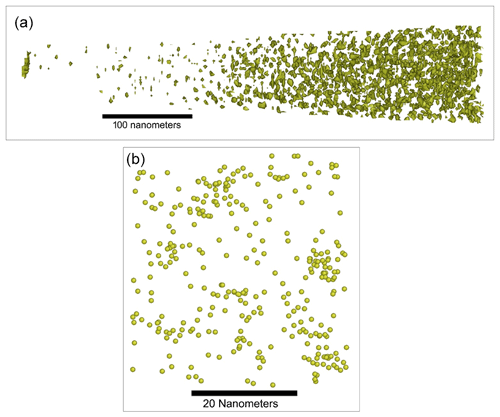
Figure 10 (a) Distribution of 0.2 at % U isoconcentration surfaces (about 10 times the background value) delineating U clusters in sample M5. (b) Each yellow sphere represents a single U atom in a 40 nm × 40 nm × 20 nm sub-domain, illustrating the clustered distribution of U.

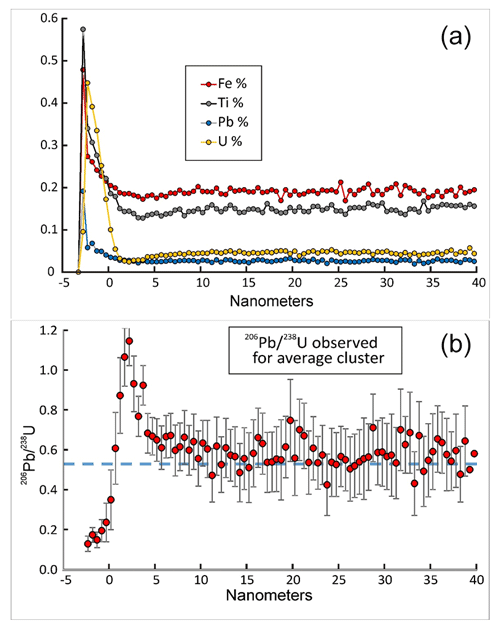
Figure 11 (a) Average Fe, Ti, U, and Pb profiles around U clusters in sample M5. A distance of zero represents the location of the average cluster boundary, and distance is negative within the boundary. The two values at the lowest (negative) distances are too imprecise to be meaningful. (b) Measured average ${}^{\mathrm{206}}\mathrm{Pb}{/}^{\mathrm{238}}\mathrm{U}$ profile around U clusters in sample M5. The blue line marks the equilibrium ${}^{\mathrm{206}}\mathrm{Pb}{/}^{\mathrm{238}}\mathrm{U}$ ratio. Modelling with assumed average recoil (R) values above 1 nm produces similar profiles, meaning that clusters cannot be used to constrain realistic values of R.

3.3 U clustering

About 40 % of the U in specimen M5 occurs in diffuse clusters of ∼10 nm diameter spaced approximately 20 nm apart. The clusters were quantified and averaged using the proximity histogram (proxigram) method of Hellman et al. (2000) with results shown in the supplementary data repository, File 3. U clusters are most visible on the mp4 rotating image file for U (supplementary data repository, File 4) and in the images in Fig. 10 showing isoconcentration surfaces and the distribution of U atoms in a local region at a 50 nm scale. “Clusters” is used to describe the regions of relatively high concentration of the atoms of interest, while “matrix” refers to the parts of the crystal between the clusters. On average, clusters are enriched in U (2406 ppma), Pb (305 ppma), Ti (1614 ppma), and Fe (2400 ppma) compared to the matrix (U = 225 ppma; Pb = 145 ppma; Ti = 712 ppma; Fe = 2086 ppma) as shown in Fig. 11a and the supplementary data repository, File 3. Although enriched within the U clusters, Pb clumping is less evident (supplementary data repository, File 5). The Hf composition is unchanged between the clustered or matrix domains. The U clusters are observed in all parts of the dataset, even at U concentrations as low as 150 ppma. No clusters were observed in specimen M2, in which U and Pb were homogeneously distributed.

For specimen M5, the entire specimen yields a ${}^{\mathrm{206}}\mathrm{Pb}{/}^{\mathrm{238}}\mathrm{U}$ ratio of 0.528±0.011 for a calculated age of 2734±70 Ma and a ${}^{\mathrm{207}}\mathrm{Pb}{/}^{\mathrm{206}}\mathrm{Pb}$ ratio of 0.179±0.017 for an age of 2640±162 Ma. The matrix domain of the sample yields a ${}^{\mathrm{206}}\mathrm{Pb}{/}^{\mathrm{238}}\mathrm{U}$ ratio of 0.772±0.020 for a calculated age of 3687±128 Ma and a ${}^{\mathrm{207}}\mathrm{Pb}{/}^{\mathrm{206}}\mathrm{Pb}$ ratio of 0.165±0.019 for an age of 2507±193 Ma. The combined clusters composition is 0.168±0.007 for the ${}^{\mathrm{206}}\mathrm{Pb}{/}^{\mathrm{238}}\mathrm{U}$ ratio and a ${}^{\mathrm{206}}\mathrm{Pb}{/}^{\mathrm{238}}\mathrm{U}$ age of 1002±46 Ma and a ${}^{\mathrm{207}}\mathrm{Pb}{/}^{\mathrm{206}}\mathrm{Pb}$ ratio of 0.232±0.042 for a ${}^{\mathrm{207}}\mathrm{Pb}{/}^{\mathrm{206}}\mathrm{Pb}$ age of 3067±292 Ma. In this dataset, the ²⁰⁷Pb${}^{++}$ peak suffered a high background due to the thermal tail of the ²⁰⁶Pb${}^{++}$ peak, detrimental for the precise quantification of ²⁰⁷Pb. The Pb content of specimen M2 was not high enough to calculate meaningful ${}^{\mathrm{206}}\mathrm{Pb}{/}^{\mathrm{238}}\mathrm{U}$ and ${}^{\mathrm{207}}\mathrm{Pb}{/}^{\mathrm{206}}\mathrm{Pb}$ ratios.

The average measured ²³⁸U and ²⁰⁶Pb concentrations and ${}^{\mathrm{206}}\mathrm{Pb}{/}^{\mathrm{238}}\mathrm{U}$ ratios within and outside the M2 clusters are shown in Fig. 11a and b, respectively, where radial bins are taken as 0.5 nm wide. The volume and number of atoms rapidly decrease as the centre of the cluster is approached, so measurement errors become large (Fig. 11a). Any measurements deeper than this are too imprecise to be meaningful. Proxigram results, such as the average ${}^{\mathrm{206}}\mathrm{Pb}{/}^{\mathrm{238}}\mathrm{U}$ ratio in the matrix (Fig. 11b), are not as statistically robust as those quoted in the paragraph above, which are the result of more thorough data processing. The average cluster is seen to have a radius of about 3.5 nm.

4 Discussion

4.1 The meaning of alpha recoil constraints from APT

The 80 nm alpha recoil constraint is significantly higher than the average recoil distance of 24±7 nm found from depth profiling of natural surfaces of baddeleyite crystals using SHRIMP (Davis and Davis, 2018) and theoretical estimates for zircon (Nasdala et al., 2001). Thermal diffusion of Pb would have a similar effect to alpha recoil and would give too large a recoil distance if it had occurred, but this is not possible over the geologic history of the sample since the metamorphic grade does not exceed greenschist facies and metamorphism occurred early in the history of the sample. The only other possibility is if the sample were heated enough during FIB milling to allow significant Pb diffusion, but this would likely require temperatures in excess of 1000 °C. Effects of heating have not been seen in other minerals with lower melting points, indicating that the temperature must have been well below that required for diffusion of Pb during the ca. 2 min period of milling.

If recoil distances in an ordered lattice are highly anisotropic, this might result in a higher than average value normal to a crystal face. This seems inconsistent with the result from SHRIMP data but the SHRIMP measurements were carried out with a beam size of about 30 µm, whereas the APT length x–y scale is about 3 orders of magnitude smaller. This equates to a sample volume about 6 orders of magnitude smaller and therefore more likely to preserve a perfect lattice arrangement (Smith and Newkirk, 1975) at a scale that is affected by alpha recoil. Another possible explanation is that surface roughness or unevenness in U zoning at the scale of alpha recoil effects resulted in violation of the assumption that U distribution was uniform in the x–y plane outside of the sampled volume. Figure 1b shows that the surface from which the sample was milled is not smooth at the scale of electron microscopy and that the wavelength of topographical features could be less than 1 µm. There is also a suggestion in Fig. 5 that the high- to low-U transition is not exactly planar. It will be important in future APT studies to select samples from natural (preferably (100)) surfaces that appear smooth at the scale of alpha recoil effects (Kozikowski, 2020) and/or to assure that any U zoning is uniform beyond the scale of alpha recoil effects.

4.2 U clusters

Alpha recoil from a U cluster should generate a diffuse cluster of Pb around it. The relative volumes of spherical shells around clusters increase as the cube of their radius, which means that ²⁰⁶Pb atoms recoiled from the clusters are rapidly diluted by Pb in the matrix as their distance becomes larger. The fairly uniform distribution of Pb seen around clusters (Fig. 11) shows that the average recoil distance must be larger than the average distance between clusters (about 10–20 nm, Fig. 10). Although there is an increase in ²⁰⁶Pb concentration within the cluster (Fig. 11a), this is well below the amount that would give a ${}^{\mathrm{206}}\mathrm{Pb}{/}^{\mathrm{238}}\mathrm{U}$ equilibrium ratio corresponding to the age of the sample (about 0.5). As mentioned above, the ${}^{\mathrm{206}}\mathrm{Pb}{/}^{\mathrm{238}}\mathrm{U}$ ratio in the interior of the cluster is about 0.17. This might be explained if the clusters formed at about 1 Ga and the recoil distance were very small (<1 nm), but there is no reason to expect U mobility at low temperatures, since it is considered to have a blocking temperature even higher than that of Pb, at least in zircon (Cherniak and Watson, 2003), or if recoil distance is negligible (see above). There is also a narrow peak in the radial ${}^{\mathrm{206}}\mathrm{Pb}{/}^{\mathrm{238}}\mathrm{U}$ ratio at about 5 nm, where it rises above 1 due to the fact that the U concentration decreases near the average cluster boundary (Fig. 11b). Away from the average cluster the background U and Pb concentrations should reflect the equilibrium ${}^{\mathrm{206}}\mathrm{Pb}{/}^{\mathrm{238}}\mathrm{U}$ ratio for the 2.7 Ga age of the sample, but in fact the density of clusters is high enough to give the matrix a significantly higher value.

The presence of the small ²⁰⁶Pb peak within the average cluster, as well as the trough in U concentration around it, cannot be explained by alpha recoil. They are most likely primary effects of cluster formation and the depletion of the silicate melt in proximity to the preferential sorption of the U ions in the clusters. The ²⁰⁶Pb peak might correspond to elevated concentrations of common Pb, which might be confirmed with ²⁰⁷Pb measurements if this mass could be effectively resolved. The trough in U concentration is perhaps due to freezing in of a U concentration gradient in the crystal or melt following growth of the high-U clusters.

The U composition of the clusters in specimen M5 differs by almost a factor of 10 from the composition of the matrix. Although the clusters are primarily composed of (Zr, Hf)O₂, they show elevated concentrations of Fe and Ti in addition to U. Thus, they are nanoscale baddeleyite domains enriched in trace elements. To the authors' knowledge, this is the first observation of random U clustering in a mineral used for geochronology. Planar or lamellar concentrations of U have been previously observed in zircon (Peterman et al., 2019; Zhao et al., 2023). Valley et al. (2014) measured clusters consisting of Pb, Y, and Yb (but not U) in a 4.4 Ga zircon core that was overgrown at 3.4 Ga. In this case, they concluded that clustering was due to migration of some trace elements through damaged crystal domains during metamorphism. Several mechanisms have been proposed for the formation of clusters in other minerals by secondary processes, including annealing of radiation damage (Peterman et al., 2021; Verberne et al., 2020), phase exsolution during cooling (Fougerouse et al., 2018), deformation (White et al., 2018b; Fougerouse et al., 2019), and fluid alteration (Joseph et al., 2023). Neither sample was subjected to metamorphism above greenschist facies (Ramsay et al., 2019; Tait et al., 2013), nor is there evidence of fluid alteration, deformation, or exsolution. Thus, the U distribution in M5 appears to be a result of primary crystallization.

The mechanism by which the clusters formed is unknown, but oscillatory zoning of U, which also appears to be present in sample M5, may be a related process. There is insufficient information from the present experiment, such as observations of zoning patterns and extent of U clustering in different zones, to undertake a detailed analysis of either, and it is difficult to envision any magmatic crystallization process that could result in nanoscale spherical clusters of trace elements. Any secondary process would have to result in very early diffusion of U, which should require pervasive structural adjustment of the crystal. One possibility might be if the original crystal formed as ziroite, a recently identified tetragonal form of ZrO₂ (Ma et al., 2023). This form was found as micrometre-scale clusters associated with baddeleyite in melt inclusions in mantle-derived corundum. Its presence in a mantle-derived assemblage suggests that the tetragonal form of ZrO₂ is stable at high pressure. If the original crystal had formed at high pressure within the plume magma and been transported into the crust, the baddeleyite crystals might spontaneously revert to their stable monoclinic low-pressure form at magmatic temperature. Such a recrystallization might allow diffusion of U, but it is unclear why U atoms would tend to nucleate.

The observation of surface roughness in Fig. 2b across the (001) face suggests either that growth of this face was a highly irregular process, in contrast to the (100) and (010) faces, which appear smooth or it is a broken surface. As mentioned above, the ${}^{\mathrm{206}}\mathrm{Pb}{/}^{\mathrm{238}}\mathrm{U}$ profile and alpha recoil modelling suggest that U concentration outside the surface was very low, although this is not definitive proof that it is not a broken surface. Clearly more grains from this sample need to be examined along with APT analysis of U distributions next to crystal surfaces and within crystals.

5 Conclusions

The original aim of the experiment was to determine the Pb depletion profiles near natural faces of two baddeleyite crystals from separate samples in order to constrain the average alpha recoil distance of daughter nuclides from U decay. In the case of the Hart Dolerite baddeleyite (M2), no such profile was observed, suggesting that the boundary was cleavage related. In the case of baddeleyite from the Great Dyke of Mauritania (M5), the measured profile strongly suggests that it was a natural crystal boundary, but the zoned distribution of U obscures the normal drop-off in $\mathrm{Pb}/\mathrm{U}$ that would be expected. Preliminary results of modelling suggest an R of about 80 nm, based on the assumptions that the observed U compositional gradient was due to internal zoning and is uniform on the x–y plane and that the modified radiogenic Pb compositional gradient is due to alpha recoil. A more precise estimation is prevented by the limited size of the APT field of view, which prevents knowledge of the composition over the entire range affected by recoil. The 80 nm estimate is much higher than that obtained from depth profiling of natural baddeleyite crystal surfaces using SHRIMP (24±7 nm, Davis and Davis, 2018). This might be explained if recoil distances are strongly anisotropic and a high degree of order was preserved adjacent to the crystal boundary at the small scale of the sample. Alternatively, surface roughness may have modified the assumption of laterally uniform U zoning, resulting in a high apparent recoil value. APT is an effective tool that could provide a much better constraint from analysis of well-characterized crystal boundaries with uniform U concentration profiles, but it is important to establish that the sampled grain surface is smooth at the scale of alpha recoil effects.

This sample also shows evidence of U clusters with radii of a few nanometres. We conclude that these clusters are primary, formed during or close to initial crystallization of the baddeleyite. Depletion of radiogenic Pb within the clusters constrains alpha recoil distances to be more than a few nanometres. The clusters nevertheless show anomalously high Pb, although much less than for radioactive equilibrium, as well as high Fe and Ti concentrations and U depletion around their margins. Explaining their formation remains a challenge for crystal chemistry. Though it is impossible to extract meaningful ages from limited (ca. 100 nm) regions of the crystal due to Pb redistribution, when using the entire APT volume meaningful ages can be calculated that correspond to those obtained using the TIMS method.