Controls on zircon age distributions in volcanic, porphyry and plutonic rocks

The distribution of zircon crystallisation ages in igneous rocks has been proposed to provide insights into the dynamics of underlying magma reservoirs. However, the ability to interpret magmatic processes from an age distribution is challenged by a complex interplay of factors such as sampling biases, analytical uncertainties and incorporation of extraneous zircon grains. Here, we use a compilation of igneous zircon U–Pb ages measured by chemical abrasion isotope dilution thermal ionisation mass spectrometry (CA-ID-TIMS) to quantify the differences that exist among zircon U–Pb age distributions from different magmatic systems. The compiled dataset was rigorously filtered through a number of processing steps to isolate age distributions least impacted by sampling biases and analytical factors. We also filter the database using a new algorithm to systematically identify and remove old outliers from age distributions. We adopt the Wasserstein distance as a dissimilarity metric to quantify the difference between the shapes of age distributions. Principal component analysis (PCA) of a dissimilarity matrix of pairwise Wasserstein distances between age distributions reveals differences among zircon age distributions found in plutonic, porphyry and volcanic rocks. Volcanic and porphyry zircon populations exhibit a skew towards younger ages in their distributions, whereas plutonic age distributions skew towards older ages. We use a bootstrap forward modelling approach to generate synthetic zircon age distributions, which are cast into the PCA space of the dissimilarity matrix of natural age distributions to allow us to identify the magmatic processes which reproduce distributions found in natural data. We find that the younger skew of porphyry and volcanic zircon age distributions can be reproduced under bootstrap sampling scenarios where zircon crystallisation is truncated (e.g. by volcanic eruption or porphyry dyke emplacement). We also find that sampling underlying zircon age distributions generated under higher magmatic flux can contribute to the younger skew of volcanic and porphyry zircon age distributions, though we emphasise that no difference in flux is required due to the strong effect of truncation. Given the multitude of factors that influence observed zircon age distributions, we urge caution when quantifying the thermal evolution of crustal magma bodies using zircon age distributions integrated with numerical models.

1 Introduction

U–Th–Pb geochronology of zircon in igneous rocks provides key information about the age, longevity and emplacement rates of magma reservoirs. Historically, the achievable age resolution limited these insights to a singular “age”, but as analytical precision and accuracy have improved, it has become possible to resolve extended records of zircon crystallisation within a single igneous rock sample. These zircon crystals can predate the eruption or final solidification of a magma body by as much as a million years (Brown and Fletcher, 1999; Wotzlaw et al., 2013; Barboni et al., 2015; Samperton et al., 2015; Szymanowski et al., 2019). The observed zircon populations may result from cooling of the magma volume in which they are found (i.e. they are autocrystic; Wotzlaw et al., 2013; Samperton et al., 2015) or they could reflect the juxtaposition of zircon populations that derive from multiple depths within the crustal column (e.g. Schoene et al., 2012; Farina et al., 2018). While still relatively under-explored, distributions of zircon ages are promising recorders of processes that are critical to the ultimate fate of the host magmatic system (e.g. a volcanic eruption or economic mineralisation). In several studies, zircon age distributions have been shown to match those produced from zircon solubility models and have thus been interpreted as the product of monotonous cooling of the magmatic system (Samperton et al., 2017; Keller et al., 2018). Others have documented age distributions which differ from these zircon solubility models and have attributed this to competition between cooling and recharge of the magma reservoir, which shifts the peak in the distribution to younger ages (Schmitt et al., 2023; Tavazzani et al., 2023a). Coupling of zircon age distributions with outputs from numerical models has been used to quantify magmatic fluxes (Caricchi et al., 2014, 2016; Weber et al., 2020; Liu et al., 2021; Schmitt et al., 2023) and to propose that greater fluxes exist in magma reservoirs forming super-eruptions compared to plutonic complexes (Caricchi et al., 2014).

Figure 1 A comparison of three visualisation approaches employed in geochronology using an example zircon U–Pb ID-TIMS dataset from the Youngest Toba Tuff (Szymanowski et al., 2023). (a) Ranked age plot (youngest to oldest) where the horizontal extent of the bars indicates the 2σ uncertainty of each U–Pb date. (b) Kernel density estimate (KDE) using both unweighted (dashed) and weighted (solid) estimates as well as the (c) weighted (dashed) and unweighted (solid) empirical cumulative distribution function (ECDF) curves, both scaled between the onset and end of zircon crystallisation (t_rel).

Isolating the effect of cooling and recharge processes on zircon age distributions can be challenging since a number of analytical and geological factors may play a role (Klein and Eddy, 2023). Firstly, a key requirement of this comparison is the ability to confidently resolve differences in crystallisation age within a single rock sample, i.e. to ensure that the observed distribution is controlled by geological dispersion rather than analytical uncertainty. This ability, best described by the apparent duration of zircon crystallisation with respect to the size of average analytical uncertainties of a dataset ($\mathrm{\Delta }t/\mathit{\sigma }$), varies with the employed analytical technique, the time range of zircon crystallisation and absolute age. Datasets also contain variable numbers of zircon dates per sample and the ability to accurately capture the underlying age distribution increases with the number of zircons analysed (Caricchi et al., 2016; Tavazzani et al., 2023a). Interpreting age distributions is further challenged by the termination of zircon crystallisation at intermediate crystallinity by dyke emplacement or volcanic eruption (a process we refer to herein as “truncation”), whereas in plutonic systems zircon crystallisation likely continues until the solidus (Samperton et al., 2017; Ratschbacher et al., 2018). Comparing age distributions is also complicated due to the challenge in identifying whether these zircons crystallised from the youngest magmatic pulse (i.e. “autocrysts”) or are a cargo of zircons crystallised in multiple, discrete systems that were incorporated upon transport (“antecrysts”) (Miller et al., 2007).

As the geochronology community presents a growing number of zircon age distributions from different magmatic systems with sufficiently long duration to analytically resolve an age distribution, constraining the controls on their distributions is becoming increasingly relevant. The number of available datasets has now become sufficient to perform systematic analyses of published data to identify patterns that can be meaningfully attributed to geological processes. Such a comparison requires a robust statistical approach which is capable of comparing distributions with varying dataset size and analytical uncertainty without making assumptions about the shape of the distribution. The use of dissimilarity metrics, such as the Kolmogorov–Smirnov and Wasserstein distances, is becoming increasingly popular to compare age distributions, with successful applications to tracing sediment provenance in multi-sample datasets (Vermeesch, 2013; Lipp and Vermeesch, 2023). These approaches are objective and they can be applied pairwise to datasets with infinite numbers of distributions and can be visualised using dimensionality reduction techniques (Vermeesch, 2013).

In this study, we compare zircon age spectra from 70 igneous units using the Wasserstein dissimilarity metric to constrain whether differences in age spectra may reflect variable dynamics of magmatic systems. We identify key differences between age distributions in plutonic, volcanic and porphyry lithologies and use a bootstrap modelling approach to explore the key factors controlling the variability of zircon age distributions in magmatic systems.

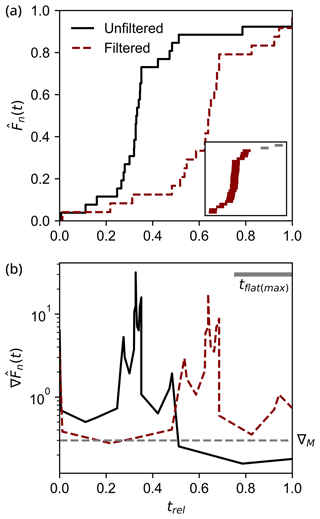
Figure 2 An example of the methodology used to filter older age populations from the age distribution of a sample from the Orano dyke swarm, Elba island (Barboni et al., 2015). Panel (a) shows the weighted ECDF of the age distribution before and after the filtering process. The inset diagram shows the ranked age plot (not scaled by the uncertainty), with grey bars highlighting the two dates that were filtered by the method (uncertainties are not shown). Panel (b) shows the gradient of the ECDF ($\mathrm{\nabla }{\widehat{F}}_n\left(t\right)$) before and after filtering. The dashed horizontal grey line indicates the gradient cut-off (∇_M), below which some degree of inheritance is deemed to have taken place if the distance in scaled age is greater than the threshold ($t_{{\mathrm{flat}}_{\max }}$).

2 Methodology

2.1 Zircon U–Th–Pb age spectra and their visualisation

The high precision allowed by state-of-the-art U–Th–Pb dating techniques is showcased in rank-order plots of zircon dates from a single sample (Fig. 1a). In this scenario, zircon dates exhibit dispersion between the onset of zircon crystallisation (i.e. initial zircon saturation, t_sat) and the end of zircon crystallisation (t_end), which represents an eruptive event or the final solidification of a magma batch. These are often treated as a scaled relative zircon crystallisation distribution, f_xtal(t_rel), where t_rel is the relative time scaled between t_sat and t_end (Keller et al., 2018):

$$\begin{array}{}\text{(1)}& t_{\mathrm{rel}}={\displaystyle \frac{t-t_{\mathrm{end}}}{t_{\mathrm{sat}}-t_{\mathrm{end}}}}.\end{array}$$

The f_xtal(t_rel) of a sample can be visualised as a kernel density estimate (KDE; Fig. 1b), which is where a series of kernels (typically Gaussian) of a fixed width (the “bandwidth”) are stacked along the distribution (Vermeesch, 2012). The main advantage of KDE plots is their ability to represent the distribution of zircon dates in an intuitive manner; moreover, they can be weighted by the variable analytical uncertainties associated with each zircon date. Another method for visualising such age distributions is an empirical cumulative distribution function (ECDF; Fig. 1c), which is a step function that increases by $\mathrm{1}/n$ (or by an interval inverse to the analytical uncertainty) at each of the n dates. The ECDF, though less intuitive, presents several advantages. The first is that outliers (e.g. xenocrysts) can be more easily identified because it is a step function that plots each discrete date unlike a KDE plot. The second is that it can be more intuitively related to dissimilarity metrics (e.g. the Kolmogorov–Smirnov test and the Wasserstein distance) which are related to the distances between two ECDFs. We thus henceforth prefer to visualise age distributions as ECDFs.

2.2 Filtering of outliers in age distributions

The biggest obstacle to identifying a truly “magmatic” age distribution is the presence of entire zircons or zircon domains (e.g. crystal cores) which are foreign to the youngest magmatic pulse, introduced into the magma via assimilation or mixing during emplacement or transport. Zircon crystals that formed within the youngest magmatic pulse are typically defined as autocrysts, and those that crystallise in an earlier magmatic pulse related to older pulses of the composite, longer-term magmatic system are often termed antecrysts (Miller et al., 2007). “Xenocrysts” are those incorporated from host rocks and are typically millions of years older, which makes them easier to exclude than antecrysts.

When analysing datasets of concordant U–Pb dates, identifying antecrysts in an age distribution is subjective. Many recent interpretations of zircon age–composition datasets acknowledge that zircon populations found in individual igneous rocks commonly represent crystallisation in complex magmatic plumbing systems (e.g. Szymanowski et al., 2019; Pamukçu et al., 2022), thereby making the autocryst–antecryst divide ambiguous and possibly detrimental to the understanding of the underlying system. Some authors may decide to exclude older tails of age distributions from their interpretation, but the criteria to do so are variable and often not clearly outlined. In some studies this can be based on different trace element compositions of older zircon, inferring they were derived from an unrelated magmatic pulse (e.g. Gagnevin et al., 2010; Siégel et al., 2018; Tavazzani et al., 2023a). Other studies may also use “breaks” in the age distribution to indicate that the older zircon crystals were derived from a different source (e.g. Samperton et al., 2015).

In this study, we present a method to filter old outliers from age distributions using constant criteria. The algorithm removes older outlier dates from an age distribution which are separated from the rest of the dataset by a fixed relative time gap. Because old outliers introduce low-gradient regions on an ECDF (e.g. black curve in Fig. 2), we identify potential antecrysts based on the gradient of an ECDF (Fig. 1c). The model first calculates the gradient of an ECDF, where ${\widehat{F}}_n\left(t_{\mathrm{rel}}\right)$ is the interpolated ECDF:

$$\begin{array}{}\text{(2)}& \mathrm{\nabla }{\widehat{F}}_n\left(t_{\mathrm{rel}}\right)={\displaystyle \frac{\mathrm{d}{\widehat{F}}_n\left(t_{\mathrm{rel}}\right)}{\mathrm{d}{t}_{\mathrm{rel}}}}.\end{array}$$

A gradient cut-off term (∇_M) is then defined that represents the gradient below which a segment of an ECDF will be defined as marking a discontinuity in the age distribution (Fig. 2). For a scaled age distribution, we then sum the length of the flat segments of the ECDF older than the two youngest dates (to ignore age gaps at the young end of the distribution, which are not considered here):

$$\begin{array}{}\text{(3)}& t_{\mathrm{flat}}=\sum _{i=\mathrm{3}}^{n_{\mathrm{zircon}}-\mathrm{1}}\left\{\begin{array}{cc}{t}_{i+\mathrm{1}}-t_i& \text{if }\mathrm{\nabla }{\widehat{F}}_n\left(t_i\right)<{\mathrm{\nabla }}_M\\ \mathrm{0}& \text{otherwise.}\end{array}\right.\end{array}$$

This metric t_flat then provides a quantification of the scaled age duration that is not continuously covered with U–Pb dates (Fig. 2). For age distributions with two discontinuous age populations, t_flat will scale with increasing temporal distance between the two populations. The choice of t_flat that is deemed acceptable ($t_{{\mathrm{flat}}_{\max }}$) for such an age distribution is subjective (i.e. at a low t_flat the two age populations will be considered continuous).

If an age distribution yields $t_{\mathrm{flat}}<t_{{\mathrm{flat}}_{\max }}$ it is deemed to come from one continuous age population. In the opposite case (i.e. $t_{\mathrm{flat}}>t_{{\mathrm{flat}}_{\max }}$), the oldest date is iteratively removed until a continuous age population ($t_{\mathrm{flat}}<t_{{\mathrm{flat}}_{\max }}$) is obtained. The two parameters ∇_M and $t_{{\mathrm{flat}}_{\max }}$ were tuned until the filtering method was satisfactory in discarding significantly older dates throughout the data compilation and did not filter those which were potentially part of the main age population. The optimal parameters determined for ∇_M and $t_{{\mathrm{flat}}_{\max }}$ are 0.30 and 0.25, respectively. Our method has functionality to perform filtering on weighted ECDFs (i.e. taking into account analytical uncertainty) but we did not implement it as it proved challenging to select constant parameters that would filter all datasets to an acceptable degree. We emphasise that our approach does not aim to provide a geologically significant method to isolate autocrystic zircons (which is impossible to verify), but rather a systematic method of isolating the dominant, continuous population (corresponding to the main magmatic pulse) across multiple datasets.

2.3 Igneous zircon geochronology compilation

Making interpretations about the dynamics of magma reservoirs from zircon age distributions requires confidence that the dispersion exhibited by the dataset is predominantly geological rather than analytical. One requirement is a sufficiently long duration of zircon crystallisation in a sample relative to the average analytical uncertainty ($\mathrm{\Delta }t/\mathit{\sigma }$, as used by Keller et al., 2018). A high $\mathrm{\Delta }t/\mathit{\sigma }$ allows the shape of a distribution to be deconvolved from analytical uncertainties, whereas age distributions with low $\mathrm{\Delta }t/\mathit{\sigma }$ are dominated by analytical uncertainty. Sufficient $\mathrm{\Delta }t/\mathit{\sigma }$ in individual magmatic systems is generally only achieved by two analytical techniques: ²³⁰Th–²³⁸U disequilibrium dating applied to young zircon (predominantly obtained with in situ methods such as secondary ion mass spectrometry – SIMS – or laser ablation inductively coupled plasma mass spectrometry – LA-ICP-MS) and high-precision U–Pb geochronology by (chemical abrasion) isotope dilution thermal ionisation mass spectrometry – (CA-)ID-TIMS (Schaltegger et al., 2015). The ²³⁰Th–²³⁸U method achieves variable, percent-level precision, which may be sufficient to resolve age distributions in the young rocks it is best suited to (< ca. 300 ka; Schmitt, 2011). However, difficulty in calculating reliable individual zircon model ages in the absence of a matching coeval melt or other mineral phase, the effective upper age limit of ca. 300 ka, and a focus of existing datasets on volcanic rocks limit the utility of ²³⁰Th–²³⁸U data for our study. On the other hand, CA-ID-TIMS U–Pb geochronology applied to samples from ca. 100 ka to the age of the solar system achieves a typical precision of ${}^{\mathrm{206}}\mathrm{Pb}{/}^{\mathrm{238}}\mathrm{U}$ dates between 0.01 %–1 % and is widely applied to plutonic, subvolcanic (i.e. porphyry) and volcanic zircon (Schoene, 2014). Given that the resolving power of U–Pb geochronology decreases with increasing age, we focused our analysis exclusively on CA-ID-TIMS data for the ${}^{\mathrm{206}}\mathrm{Pb}{/}^{\mathrm{238}}\mathrm{U}$ chronometer most applicable to young (<1 Ga) rocks.

In order to systematically compare zircon age distributions between different magmatic systems, we adopted a previously compiled database of published zircon U–Pb dates (Markovic et al., 2024). We classified and sub-selected data from samples clearly identifiable as either plutonic, porphyry or proximal volcanic deposits. This permits a comparison of age distributions in a diverse range of igneous rocks. We excluded distal volcanic materials such as ash beds or bentonites to avoid biases related to transport sorting or included detrital material. While complete exclusion of cases of Pb loss is not verifiable, we focused our analysis on samples least affected by radiation damage, only considering datasets with age <130 Ma. Rare cases of clear young outliers remaining in the database were excluded manually.

We only include age distributions with an apparent $\mathrm{\Delta }t/\mathit{\sigma }$ greater than 10 to provide confidence that the age distribution is sufficiently dispersed to isolate geological dispersion from analytical dispersion. Resolving an age distribution also requires a sufficient number of dates (n_zircon) from a magmatic unit. Many studies often report a small number of dates (e.g. five or fewer), and in such scenarios the underlying age distribution is likely undersampled. The final dataset was thus limited to include only inheritance-filtered distributions that contained a minimum of 10 dates, as previous works indicate that sampling with fewer than 10 zircon dates fails to capture the underlying distribution (Klein and Eddy, 2023; Tavazzani et al., 2023b). We additionally found that some age distributions contain dates with highly variable analytical uncertainties, with some containing over an order of magnitude variation in uncertainties for zircon crystals dated from the same rock. Individual dates with high uncertainty in an age distribution impact the ability to resolve geological dispersion and in many cases would not be filtered using the apparent $\mathrm{\Delta }t/\mathit{\sigma }$. We therefore calculate the weighting w that each date i holds in an age distribution using the inverse squared uncertainty (McLean et al., 2011):

$$\begin{array}{}\text{(4)}& w_i={\displaystyle \frac{\frac{\mathrm{1}}{{\mathit{\sigma }}_i^{\mathrm{2}}}}{{\sum }_{i=\mathrm{1}}^{n_{\mathrm{zircon}}}\frac{\mathrm{1}}{{\mathit{\sigma }}_i^{\mathrm{2}}}}}.\end{array}$$

Age distributions with a standard deviation of w_i exceeding 0.08 were discarded. The final, filtered compilation contained 70 U–Pb age distributions from 22 magmatic systems (Figs. 3, S1; Tables 1 and S1).

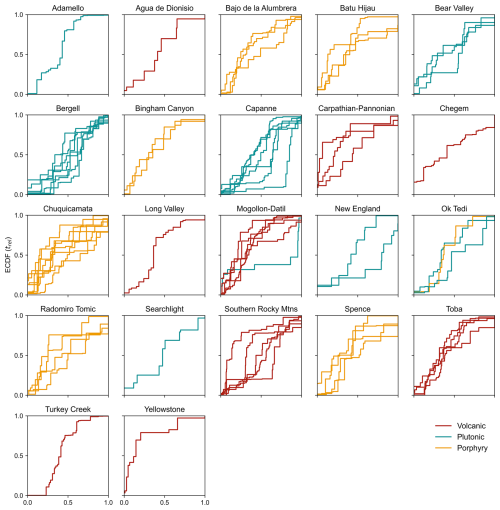
Figure 3 Weighted empirical cumulative distribution function curves for all 70 filtered zircon age distributions used in this study. Plots are separated based on the locality, and curves indicate individual geological units within the locality. The colour of each curve reflects the sample classification as volcanic (blue), plutonic (red) and porphyry (yellow) in the database.

Schoene et al. (2012)Buret et al. (2017)Buret et al. (2016)Large et al. (2020)Samperton et al. (2015)Large et al. (2021)Barboni et al. (2015)Brlek et al. (2023)Bindeman et al. (2021)Virmond et al. (2024)Ickert et al. (2015)Rioux et al. (2016)Szymanowski et al. (2019)Gaynor et al. (2023)Kinney et al. (2021)Large et al. (2018)Virmond et al. (2024)Eddy et al. (2022)Wotzlaw et al. (2013)Curry et al. (2021)Bunker (2020)Szymanowski et al. (2023)Deering et al. (2016)Wotzlaw et al. (2015)

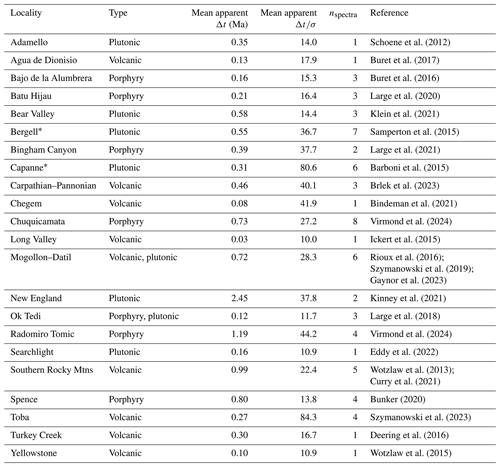
Table 1 Sources of data used in the filtered zircon CA-ID-TIMS U–Pb database and metadata describing the type of magmatic emplacement (plutonic, volcanic or porphyry), the mean Δt and $\mathrm{\Delta }t/\mathit{\sigma }$, and the number of spectra present in the database for each locality.

^* Age distributions contain sub-grain analyses.

2.4 The Wasserstein distance

The Wasserstein distance arises from the field of optimal transport and is a metric that allows comparison of two probability distributions. The metric is often termed the “earth mover's distance” because each probability distribution can be treated as a mound of earth, where the minimum cost of transferring earth from one mound to the other is the amount of earth multiplied by the distance it must be moved (Villani, 2003). Thus, the Wasserstein distance seeks to find the most efficient transport plan, which is the minimum cost of transporting one distribution to another. The optimal transport plan between two distributions is a measure of the dissimilarity of two distributions, with more dissimilar distributions requiring a greater cost and resulting in a larger Wasserstein distance. For two age distributions, μ and ν, with cumulative distribution functions (CDFs) M and N, the pth Wasserstein distance between them is given as

$$\begin{array}{}\text{(5)}& W_p(\mathit{\mu },\mathit{\nu })={\left(\underset{\mathrm{0}}{\overset{\mathrm{1}}{\int }}{\left|M^{-\mathrm{1}}-N^{-\mathrm{1}}\right|}^p\mathrm{d}t\right)}^{\frac{\mathrm{1}}{p}}.\end{array}$$

The W₁ distance (i.e. where p=1) is equal to the area between two ECDFs (Fig. 4). However, we follow the approach of Lipp and Vermeesch (2023) and implement the Wasserstein-2 distance (W₂) which is the squared distance (p=2) and is akin to the standard distance metric used in most statistical analyses. The Python package Python Optimal Transport (v. 0.9.4 Flamary et al., 2021) is used for all optimal transport computations. Zircon age datasets are discrete data and do not follow a continuous probability distribution; as such, the Wasserstein distance applies to their empirical cumulative distribution functions (ECDFs). In the case of ID-TIMS datasets, each date is not expected to hold equal weight due to variable analytical uncertainties. Thus, the probability distributions μ and ν can be represented as the weighted sum of p and q delta functions δ (Lipp and Vermeesch, 2023):

$$\begin{array}{}\text{(6)}& \mathit{\mu }=\sum _i^p{m}_i{\mathit{\delta }}_{x_m},\mathit{\nu }=\sum _i^q{n}_i{\mathit{\delta }}_{x_n},\end{array}$$

where m and n are weights that sum to 1. In the case where dates do not hold equal weight in the overall distribution, weights m and n can be calculated using Eq. (4). We plot ECDFs, calculate the W₂ distance using the weights, and provide the same results calculated without weights for comparison (Figs. S2 and S3).

The Wasserstein distance has several advantages as a metric to compare zircon age distributions. In addition to allowing weighting based on uncertainty, it can be used for discrete ages (i.e. an ECDF) and does not require the inference of a specific prior distribution. The W₂ is also attractive in that, for two age distributions, it is sensitive to their location (their means), the spread (their standard deviations) and the shape of the distribution (Irpino and Romano, 2007; Lipp and Vermeesch, 2023). All three of these properties are relevant when considering two U–Pb age distributions. We prefer the Wasserstein distance to the Kolmogorov–Smirnov distance because the latter is a measure of the maximum vertical difference between the two ECDFs and is, as such, less sensitive to the overall shape of the distribution.

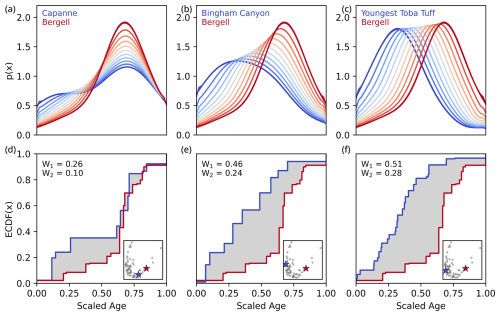
Figure 4 Examples showing three comparisons of similar to contrasting U–Pb ID-TIMS age distributions. Panels (a–c) show the distributions in blue and red with the transition distributions showing equally spaced (at 0.1 intervals) distributions in Wasserstein space (i.e. the Wasserstein barycentres). Panels (d–f) show the same two distributions as above as weighted ECDF curves, where the grey shaded area indicates the W₁ distance between the two distributions. The W₂ is also reported. Insets show where the two compared distributions plot on the PC1 versus PC2 diagram of the W₂ dissimilarity matrix (Fig. 5; see Sect. 2.5 for a description of dissimilarity matrix construction).

2.5 Dissimilarity matrix and dimensionality reduction

The W₂ metric permits pairwise comparisons of age distributions. Thus for Y age distributions, a symmetric dissimilarity matrix, d of dimension Y×Y, can be constructed:

$$\begin{array}{}\text{(7)}& d=\left[\begin{array}{cccc}{d}_{\mathrm{1},\mathrm{1}}& d_{\mathrm{1},\mathrm{2}}& \mathrm{\cdots }& d_{\mathrm{1},Y}\\ d_{\mathrm{2},\mathrm{1}}& d_{\mathrm{2},\mathrm{2}}& \mathrm{\cdots }& d_{\mathrm{2},Y}\\ \mathrm{⋮}& \mathrm{⋮}& \mathrm{\ddots }& \mathrm{⋮}\\ d_{Y,\mathrm{1}}& d_{Y,\mathrm{2}}& \mathrm{\cdots }& d_{Y,Y}\end{array}\right].\end{array}$$

Because the W₂ distance is a metric (i.e. it satisfies the triangle inequality), principal component analysis (PCA) can be applied to reduce the dissimilarity matrix to fewer dimensions whilst preserving the pairwise distances (Vermeesch, 2013; Lipp and Vermeesch, 2023). PCA aims to preserve the variance of a dataset in a lower dimension space, where for a dissimilarity matrix this reflects the pairwise distances. We use the Python implementation within sci-kit learn (v. 1.5.1 Pedregosa et al., 2011) for PCA. The first two principal components contain 90 % of the variance of the dissimilarity matrix, indicating that the majority of the pairwise distances are preserved with only 10 % being lost.

2.6 Modelling approach

2.6.1 Bootstrap forward modelling of zircon age distributions

Forward modelling of synthetic age distributions and comparison with natural data can yield insights into the controls on age distributions in magmatic systems (Caricchi et al., 2014; Schmitt et al., 2023; Tavazzani et al., 2023a). This process aims to sample an underlying zircon age distribution according to realistic uncertainties and numbers of zircons sampled for ID-TIMS datasets. The underlying distribution, or the uncertainties and number of zircons sampled, can be varied to test different hypotheses on the controls on zircon age distributions. We follow the bootstrap modelling approach of Tavazzani et al. (2023b). The model samples n_zircon synthetic dates from a probability distribution p(x) which is equivalent to a selected underlying age distribution, such as the theoretical zircon age distribution obtained from zircon solubility and thermodynamic modelling of a monotonically cooling magma reservoir (Keller et al., 2018). For simplicity, our model assumes each zircon crystallises instantaneously and does not take into account the protracted growth of each individual zircon and the inherent volumetric bias of bulk grain analyses towards younger ages (Klein and Eddy, 2023). Gaussian uncertainty is then added to each synthetic age to reproduce uncertainties reported in ID-TIMS datasets. To calculate the uncertainty at a given age, we parameterised the reported 2σ absolute analytical uncertainty in the ID-TIMS compilation of Markovic et al. (2024) as a function of ${}^{\mathrm{206}}\mathrm{Pb}{/}^{\mathrm{238}}\mathrm{U}$ age (t in Ma) up to 1000 Ma using a second-order polynomial fit. The resulting best-fit parameters and covariance matrix yield the following equation with errors given as 2 SE:

$$\begin{array}{}\text{(8)}& \begin{array}{rl}\mathrm{2}\mathit{\sigma }& =\mathrm{5.5}\times {\mathrm{10}}^{-\mathrm{7}}(\pm \mathrm{2.8}\times {\mathrm{10}}^{-\mathrm{7}})t^{\mathrm{2}}+\mathrm{8.9}\\ & \times {\mathrm{10}}^{-\mathrm{4}}(\pm \mathrm{2.0}\times {\mathrm{10}}^{-\mathrm{4}})t+\mathrm{0.040}(\pm \mathrm{0.0162}).\end{array}\end{array}$$

Gaussian uncertainty is propagated onto each date sampled during bootstrap sampling according to the standard error of the fit parameters. The bootstrap sampling can be repeated with varying numbers of zircon grains, different age (and thus different analytical uncertainties) and a different underlying distribution. These distributions can then be concatenated with the W₂ dissimilarity matrix generated on natural data. The pairwise dissimilarities of a modelled distribution with all natural distributions can then be transformed by PCA and visualised alongside natural data.

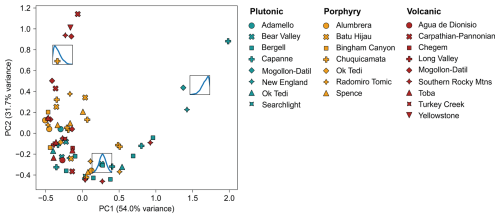
Figure 5 Results of PCA on the W₂ CA-ID-TIMS zircon U–Pb dissimilarity matrix. Each data point indicates one U–Pb age distribution (i.e. one sample or unit) for a magmatic system. The percentage variance that each principal component accounts for is given. The three inset graphs represent KDEs of skew-normal distribution with varying values of skew (−100, 0 and 100) for comparison with natural distributions.

2.6.2 Magma recharge and underlying age distributions

The underlying age distribution from which zircon U–Pb dates are sampled can vary as a function of magmatic flux and volume (Caricchi et al., 2014; Tavazzani et al., 2023a). Keller et al. (2018) showed a remarkable similarity between age distributions predicted from zircon solubility and thermodynamic models (Watson, 1996) and age distributions observed in plutons (Samperton et al., 2015). This predicts a peak in zircon crystallisation at the onset of zircon saturation which decays until the solidus, producing a skew towards older ages. However, this prediction assumes monotonous cooling of magma, while open-system behaviour can produce multi-modal age distributions with a general shift towards younger skew (Caricchi et al., 2014; Schmitt et al., 2023; Tavazzani et al., 2023a). We use the approach of Tavazzani et al. (2023b), who generated zircon age distributions representative of complex crystallisation simulations. These simulations investigate zircon crystallisation under a range of non-linear temperature–crystallinity scenarios developed using the thermodynamic modelling software Magma Chamber Simulation (Bohrson et al., 2014). This combines closed- and open-system processes such as fractional crystallisation, single recharges or repeated recharges of new magma in a magma body. Synthetic age distributions generated under varying recharge can then be compared to natural data as described above. We compare the bootstrap sampling of a zircon age distribution generated with recharge of a cooling, upper-crustal rhyolitic magma reservoir with zero, three and five recharges. Each recharge is triggered when crystallinity reaches 50 vol % and comprises an addition of 50 g of rhyolitic magma (with an initial magma reservoir mass of 100 g) with the same composition and liquidus temperature (870 °C) as the original magma (Tavazzani et al., 2023b).

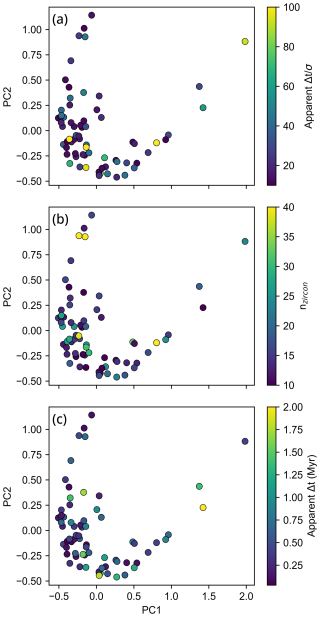
Figure 6 Plot of the PCA on the W₂ CA-ID-TIMS zircon U–Pb dissimilarity matrix coloured by (a) the ratio of zircon crystallisation duration and the mean analytical uncertainty (apparent $\mathrm{\Delta }t/\mathit{\sigma }$) as well as (b) the number of zircons in the age spectrum (n_zircon) and (c) the duration of zircon crystallisation in millions of years (Myr) (apparent Δt).

3 Results

The PCA plot of the W₂ dissimilarity matrix of the high-precision U–Pb data compilation produces a parabolic shape (Fig. 5). Because the W₂ distance is equivalent to the squared difference between two weighted ECDFs, the location of an age distribution on the plot of the PCA of the W₂ dissimilarity matrix (Fig. 5) can be compared with the shapes of the weighted ECDFs of the age distributions (Fig. 3). The distance between two age distributions on the PCA plot refers to the degree of dissimilarity between them. For example, two strongly contrasting distributions (Fig. 3), such as from a New England plutonic sample (old skew) and a Yellowstone volcanic sample (young skew), plot on opposite sides of the PC parabola (Fig. 5). By contrast, relatively homogeneous weighted ECDFs in single magmatic systems cluster together on the PC parabola (e.g. Toba).

There is a pronounced tendency for volcanic and porphyry zircon age distributions to plot further left on the parabola than plutonic age distributions, which plot on the right (Fig. 5). In order to interpret this difference, we cast skewed normal distributions onto the W₂ dissimilarity matrix which were generated with varying values of skew (see inset plots in Fig. 5). This comparison demonstrates that the position of a distribution along the PC parabola generally reflects the amount of skew of a distribution because old-skewed distributions plot in the top left of the parabola, whilst young-skewed distributions plot in the top right. Distributions that show a lack of skew (i.e. normal distributions) plot towards the centre of the parabola. Volcanic and porphyry age distributions therefore generally skew towards younger ages, whereas plutonic age distributions skew towards older ages.

Figure 7 Kernel density plots showing results of bootstrap sampling of the theoretical zircon crystallisation distribution in a monotonically cooling magma reservoir derived from thermodynamic models (Keller et al., 2018) as shown by the thick red curve. The number of zircons sampled (n_zircon) ranges from (a) 30 to (b) 10 to (c) 5, and the thin translucent red curves show 100 sampling iterations. An uncertainty is added to each age as appropriate for a sample at 10 Ma. Inset plots show the PCA of the W₂ dissimilarity matrix of natural zircon U–Pb distributions (grey symbols) and where the 100 synthetic age distributions plot (red symbols) relative to the sampled distribution (star).

4 Discussion

4.1 Controlling factors on zircon age distributions

4.1.1 Analytical factors

As discussed previously, the ability to resolve geological dispersion from an age distribution depends strongly on $\mathrm{\Delta }t/\mathit{\sigma }$. The apparent $\mathrm{\Delta }t/\mathit{\sigma }$ threshold applied to our database (>10) aims to reduce the number of age distributions which are dominated by analytical uncertainty. In order to validate our choice of apparent $\mathrm{\Delta }t/\mathit{\sigma }$ filter, we examined the position of distributions on the PC parabola relative to their apparent $\mathrm{\Delta }t/\mathit{\sigma }$ (Fig. 6a). We do not find that low values of apparent $\mathrm{\Delta }t/\mathit{\sigma }$ (i.e. close to 10) lead to a collapse of distributions towards normal distributions, indicating that these distributions are unlikely to be dominated by analytical uncertainty. We additionally find that repeating our analysis with a lower threshold of apparent $\mathrm{\Delta }t/\mathit{\sigma }$ (>5) provides similar results (Fig. S4) yet further populates the central part of the parabola, potentially indicating that these lower apparent $\mathrm{\Delta }t/\mathit{\sigma }$ distributions have less skew and are thus dominated by analytical uncertainty.

We limited our study to young CA-ID-TIMS datasets (<130 Ma) where chemical abrasion was performed to reduce the effects of Pb loss. However, we find that the conditions under which chemical abrasion was performed vary. Notably, the temperatures of chemical abrasion range between 180 and 220 °C, which can impact the measured U–Pb date (Widmann et al., 2019; McKanna et al., 2024). To exclude the possibility that the variability in shape of an age distribution could be the result of unmitigated Pb loss, we compiled the chemical abrasion temperature of zircon in each study and compared this with the position of each distribution on the PCA plot of the W₂ dissimilarity matrix (Fig. S5). If unmitigated Pb loss is present, we should find that age distributions from lower chemical abrasion temperatures plot in the top right of the PC parabola. However, we find no relationship between chemical abrasion temperature and distribution shape, which negates the possibility that the varying shape of age distributions in CA-ID-TIMS datasets is related to unmitigated Pb loss.

4.1.2 Number of zircons sampled

A decreasing number of zircon analyses (n_zircon) in an age distribution leads to a collapse of an age distribution towards a normal distribution (Tavazzani et al., 2023a). To further test the validity of our choice of n_zircon>10 as a filter, we systematically study the effect of n_zircon by sampling different numbers of zircons from the same underlying synthetic zircon crystallisation distribution in a monotonically cooling magma reservoir derived from thermodynamic models (for a full description of the methodology used to obtain this theoretical distribution see Keller et al., 2018; Tavazzani et al., 2023b). We perform this sampling for n_zircon of 5, 10 and 30 at analytical uncertainties typical for 10 Myr old zircons (Fig. 7) and provide a more extensive analysis at different zircon crystallisation ages (Fig. S6) and for n_zircon between 4 and 60 (Fig. S7). Our search space for n_zircon broadly reflects the lower, intermediate and upper range of zircon analysed per sample in the compiled CA-ID-TIMS datasets (Table S1).

Results of iterative sampling from an underlying monotonic cooling distribution highlight the loss of reproducibility of the initial distribution when n_zircon=5 (Fig. 7). This is reflected by the increasing flattening of the KDE curve and, in PCA space of the W₂ dissimilarity matrix, by a scatter of synthetic zircon distributions towards highly variable positions on the PCA plot. Undersampling of the underlying distribution can lead to a reversal of the skew in the bootstrapped distribution (i.e. plotting on the left-hand side of the PC parabola; Fig. 7). This confirms that the shape of age distributions in datasets where n_zircon<10 should not be interpreted in the context of geological variability.

Sampling a larger number of zircons (n_zircon=10) more accurately captures the skew towards older ages of the underlying distribution (Fig. 7). However, an appreciable variation is still apparent in these sampled distributions, which cover a large range of PC1 scores in the W₂ dissimilarity matrix. With an even larger number of sampled zircon dates (n_zircon=30), the variance of the sampled distributions is reduced as they more accurately reproduce the underlying distribution. However, even in the case where the number of sampled zircon dates is high (n=30), significant variation still exists in the PCA plot of the W₂ dissimilarity matrix (Fig. 7). This finding suggests that one should avoid making interpretations from small variations between different spectra on the PC parabola, since these are likely to reflect undersampling-related scatter.

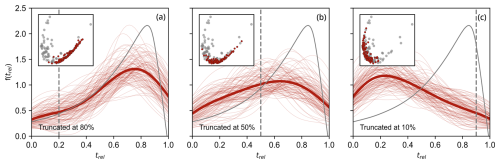
Figure 8 Modelled kernel density plots showing the effect of bootstrap-sampling an underlying distribution with different degrees of truncation of zircon crystallisation (t_rel=0.8, 0.5, 0.1) simulating melt extraction or volcanic eruption. The sampled underlying distribution (dashed grey line) is the monotonic cooling distribution (Keller et al., 2018). A total of 30 zircons are sampled for each of the 100 synthetic distributions (faint red), and the average of 100 simulations is shown (dark red). Inset plots show the location of these distributions (red symbols) on the PCA plot of the W₂ dissimilarity matrix of natural zircon U–Pb distributions (grey symbols).

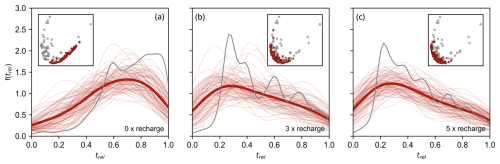
Figure 9 Modelled kernel density curves showing the effect of repeated magma recharge on zircon age distributions. Underlying zircon age distributions are produced with varying numbers of recharges of felsic melt into a felsic magma reservoir undergoing cooling and crystallisation. Underlying zircon age distributions (grey curves) are taken from Tavazzani et al. (2023b) for (a) zero, (b) three and (c) five recharge events during magma cooling. A total of 30 zircons are sampled from each of the 100 sampled distributions, and uncertainties are added as appropriate for 10 Myr old zircons (red curves). The average curve (thick opaque red) shows the average of the 100 synthetic age distributions and the progressive shift from old to young skew with an increasing number of recharges. Insets show the location of these distributions (red symbols) on the PCA plot of the W₂ dissimilarity matrix of natural zircon U–Pb distributions (grey symbols).

More detailed modelling of the effect of n_zircon on the ability to capture an underlying age distribution (Fig. S7) shows that for 10 Myr old zircons, the optimal choice of n_zircon is approximately 14 because increasing n_zircon beyond this leads to only a marginal increase in performance. At 100 Ma, producing an equivalent performance requires approximately 20 zircon grains to be dated. However, our choice of n_zircon=10 for this study can still capture an underlying distribution and a greater threshold would significantly impact the availability of natural data for this study. As larger datasets are published, the filtering threshold of n_zircon could be increased to further reduce the effect of undersampling on the shape of the age distribution.

4.1.3 Truncation of zircon crystallisation

Zircon age distributions in volcanic and porphyry rocks are produced by a characteristic crystallisation history because magma quenching upon eruption or final emplacement after zircon saturation will interrupt zircon crystallisation (Keller et al., 2018; Schmitt et al., 2023). We model the effect that “truncation” has on the resulting zircon age spectra by using the same underlying monotonic cooling zircon crystallisation distribution used above, sampled at variable degrees of t_rel, namely 0.8, 0.5 and 0.1. This simulates scenarios where a monotonically cooling igneous body erupts at a time close to the solidus relative to zircon saturation (t_rel=0.8), halfway in time between zircon saturation and the solidus (t_rel=0.5) or close in time to the onset of zircon saturation (t_rel=0.1). We model this range as volcanic products can vary between crystal-poor and crystal-rich (Hildreth, 1981) and porphyry rocks are typically crystal-rich, though we emphasise that t_start refers to the time of zircon saturation and not the liquidus. The simplified model assumes that melt quenches upon evacuation, thus abruptly terminating zircon crystallisation.

The zircon age distribution of a magma extracted at t_rel=0.8 is comparable with the distribution obtained from a monotonically cooled magma body, although some of the skew toward older ages is lost (Fig. 8). These sampled synthetic distributions produced by mild truncation of the underlying monotonic cooling distribution reproduce the spread of the natural dataset on the right arm of the PC parabola. When truncation takes place at an intermediate time between zircon saturation and the system's solidus (t_rel=0.5), the effect of truncation of the underlying monotonic cooling distribution is more evident. In this scenario, synthetic zircon age spectra lose most of their skew and largely overlap with the central axis of the natural zircon U–Pb distributions in the PC parabola (i.e. form a near-normal distribution). In the case of truncation happening at t_rel=0.1, synthetic age distributions always exhibit young skew (i.e. plot on the left of the PC parabola). In the PCA space of the W₂ dissimilarity matrix, these simulation outputs do not overlap at all with the underlying monotonic cooling zircon age distribution.

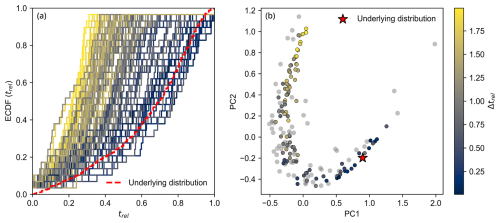
Figure 10 The effect of antecrysts on zircon age distributions for 100 simulations where 29 zircons are sampled from a primary age distribution and 1 zircon is sampled from an identical age distribution older by Δt_rel from the primary distribution. Δt_rel is randomly varied between 0 and 2, and each synthetic distribution is coloured by the magnitude of Δt_rel. (a) The ECDF of each synthetic distribution and (b) the location of each synthetic distribution on the PCA plot of the W₂ dissimilarity matrix of natural zircon U–Pb distributions. A large number of these synthetic distributions would be filtered for the antecryst if the outlier filtering method in Sect. 2.2 were employed (Fig. S8).

These results indicate that truncation can significantly alter the shape of the underlying distribution, with extreme truncation (t_rel=0.1 in our simplified model) being able to reverse the skew of a distribution. Our modelling also shows that truncation can account for most of the variability in zircon age distributions observed in natural examples. Therefore, this is likely a key factor in explaining the younger skew of volcanic and porphyry zircon age distributions relative to plutonic zircons, given that the former age distributions will be interrupted by magma evacuation and subsequent rapid cooling. We note, however, that even the most extreme effects of truncation are not able to reproduce a minority of volcanic zircon age spectra nested on the far top-left end of the PC parabola (Fig. 8).

4.1.4 Magma recharge

It has been suggested previously that differences in zircon age distributions between volcanic and plutonic systems may be linked to different fluxes in the source magma reservoir (Caricchi et al., 2014; Schmitt et al., 2023). The forward crystallisation models investigated so far assume a monotonically cooling magma reservoir without subsequent recharge (Figs. 7 and 8), which may be unrealistic for many magmatic systems (Sparks et al., 1977), where recharge will increase temperature, change melt composition and thus influence zircon crystallisation in the magmatic system (Szymanowski et al., 2020; Tavazzani et al., 2023a). We therefore consider the role of sampling different underlying distributions of zircon ages whose shape may be produced by different magma recharge histories. In these scenarios, the compositional and thermal contribution of each new magma injection acts against zircon saturation and consequently delays zircon crystallisation. We investigate the effects of an increasing number of rhyolitic melt recharges (zero, three and five recharges of 870 °C) into a cooling rhyolitic magma reservoir. The underlying distributions transition from unimodal with no recharge to increasingly multi-modal and with younger skew as the number of recharges increases (Fig. 9). With no recharge, the synthetic zircon crystallisation spectrum is equivalent to the monotonic cooling distribution and sampled distributions all exhibit older skew and are located on the right-hand side of the PC parabola. With three recharges, the synthetic distributions have predominantly younger skew and plot towards the centre and left of the PC parabola (Fig. 9). With five recharges, the synthetic distributions look broadly similar to those after three recharges, but with less variance and a slight increase in the skew towards younger ages (Fig. 9). Therefore, magma recharge appears to exert a strong control on the skew of zircon age distributions, in a manner similar to albeit less extreme than truncation of zircon crystallisation. Furthermore, like truncation, it is unable to produce the age distributions plotting at the extreme top left of the PC parabola.

4.1.5 Incorporation of antecrystic zircon

The natural age distributions that plot at the extreme top left of the PC parabola (Fig. 5) are those with a minority of zircon dates that are significantly older than the main population. Because these age distributions cannot be reproduced by the modelling performed so far, it is possible that these distributions contain antecrysts (Miller et al., 2007) that are only marginally older than the broader age distribution (and hence not identified by our filtering method). An inspection of the ECDFs of these age distributions (Fig. 3) indicates that they contain a small number of zircons (one to three) that could be from an older population.

The modelling presented so far has sampled an age distribution from a single magma reservoir. To model the effect of antecrysts on zircon age distributions, we additionally sample n_inh zircons from a second age distribution which is older than the primary age distribution in relative time by Δt_rel. The population of n_inh is then added to a primary bootstrapped age distribution consisting of n_zircon−n_inh zircons and then t_rel is renormalised between zero and 1. These modelled age distributions can then be treated identically to those modelled above and compared with natural data in the PCA W₂ space.

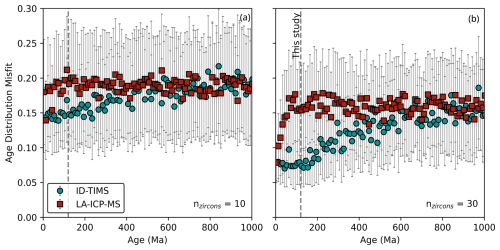
Figure 11 Comparison of the ability of ID-TIMS and LA-ICP-MS to capture the underlying zircon age distribution. At a given age, bootstrap forward modelling is applied to the monotonic cooling age distribution (Keller et al., 2018), and the Wasserstein distance is calculated between the sampled age distribution and the underlying distribution. At each age this is repeated 25 times and the mean W₂ is shown, with the error bars showing the standard deviation. The vertical dashed line shows the maximum age of ID-TIMS distributions permitted in this study. This method is repeated for (a) n_zircon=10 and (b) n_zircon = 30.

Our modelling of the effect of sampling antecrysts on age distributions shows that the presence of just one antecrystic zircon in an autocrystic population of 30 zircon U–Pb dates can have a profound effect on the final age distribution (Fig. 10). An antecryst derived from an older secondary age distribution where Δt_rel=1 (i.e. zircon crystallisation in the older distribution ended at the same time as zircon saturation in the primary, younger distribution) has a discernible effect on the age distribution, shifting it from plotting alongside older skewed datasets to where those with normal distributions plot (Fig. 10). Larger values of Δt_rel (up to 2) have an even greater effect and can produce the extreme top-left end of the PC parabola produced by the natural data.

In summary, our modelling suggests that truncation of zircon crystallisation is the most likely candidate to explain the difference between volcanic, porphyry and plutonic zircon age distributions because it is a factor that affects all volcanic and porphyry zircon age distributions and does not affect plutonic distributions. Variable magma recharge will also play a significant role yet is not required to explain the variability in natural age distributions. The most extreme young-skewed age distributions can be attributed to the incorporation of antecrysts in an age distribution. In reality, the observed zircon age spectra can be simultaneously affected by many of the geological and analytical effects discussed here, and the deconvolution of their exact contributions will be challenging.

4.2 Implications for the estimation of eruption and solidification ages

The most common application of zircon age spectra is to calculate t_end, i.e. the age of a volcanic eruption or emplacement of an intrusion (Keller et al., 2018; Ratschbacher et al., 2018). Although many authors often use the youngest measured date or the weighted mean of the youngest population of dates, Keller et al. (2018) demonstrated that a Bayesian method frequently provides the most accurate result and is least likely to underestimate uncertainty of the eruption or emplacement age.

The Bayesian approach uses prior knowledge of the zircon crystallisation spectrum (e.g. from theoretical constraints), measured zircon U–Pb age data, and their uncertainties to estimate t_end and its uncertainty. Several options exist for prior distributions such as the monotonic cooling distribution, a uniform distribution or a bootstrapped sample of the measured U–Pb dates. In some cases, the choice of prior may not greatly influence the eruption age (Keller et al., 2018), but in cases where the data are under-dispersed, analytical uncertainties are high or the number of zircons is low, greater importance is placed on prior knowledge of the zircon age distribution. Therefore, our analysis of natural zircon age distributions from young systems can inform the choice of a prior distribution. Our study shows that a monotonic cooling distribution (skew towards old ages) can be assumed for many plutonic systems but is not appropriate for volcanic or porphyry systems (Fig. 5). For volcanic and porphyry systems, a truncated distribution appears to be the most appropriate choice of prior (e.g. truncated normal, half-normal or triangular distributions; Keller, 2018) as validated by our modelling of the effect of truncation on shifting zircon age spectra towards a younger skew (Fig. 8).

4.3 Resolving zircon age distributions using different analytical techniques

The effect of geological processes versus analytical uncertainty on an age distribution will vary as a function of sample age (i.e. as absolute analytical uncertainties expand). The interpretations made in this study are based on relatively young (ca. <130 Ma) magmatic systems analysed by CA-ID-TIMS, where analytical capabilities are strongest and the potential for Pb loss is lowest. However, it is also possible that such an approach could be applicable to in situ techniques such as LA-ICP-MS for samples young enough that the large relative analytical uncertainties inherent to the technique correspond to sufficiently low absolute uncertainties.

We adapt our bootstrap model of the monotonic cooling age distribution to sample age distributions at a wider range of ages (between 0.1 and 1000 Ma) for absolute analytical uncertainties relevant to ID-TIMS and LA-ICP-MS at the given age. This uses the parameterisation of ID-TIMS uncertainties as a function of age (Eq. 8) to allow the bootstrap modelling of the monotonic cooling distribution to be performed from 0.1 to 1000 Ma. We also performed a third-order polynomial regression on 2σ absolute uncertainties reported for a compilation (Chelle-Michou and Schaltegger, 2023) of LA-ICP-MS dates (t in Ma) up to 1000 Ma with uncertainties reported as 2 SE:

$$\begin{array}{}\text{(9)}& \begin{array}{rl}\mathrm{2}\mathit{\sigma }& =\mathrm{4.0}\times {\mathrm{10}}^{-\mathrm{8}}(\pm \mathrm{8.6}\times {\mathrm{10}}^{-\mathrm{9}})t^{\mathrm{3}}-\mathrm{4.1}\\ & \times {\mathrm{10}}^{-\mathrm{5}}(\pm \mathrm{1.0}\times {\mathrm{10}}^{-\mathrm{5}})t^{\mathrm{2}}+\mathrm{0.024}(\pm \mathrm{0.0029})t\\ & +\mathrm{0.22}(\pm \mathrm{0.14}).\end{array}\end{array}$$

Gaussian uncertainty is propagated onto each date sampled during bootstrap sampling according to the standard error of the fit parameters. We perform bootstrap sampling 25 times and calculate the Wasserstein distance between the sampled age distribution and the original age distribution, which we refer to as the age distribution “misfit” (Figs. 11 and S9). We average and plot these 25 misfit scores along with their standard deviation. When the misfit is 0, the bootstrap-sampled age distribution fully reproduces the underlying distribution. As the bootstrapped distribution deviates further from the underlying distribution, the misfit increases.

When 10 zircon crystals are sampled, this analysis indicates that at young ages (<5 Ma), LA-ICP-MS and ID-TIMS can capture the underlying distribution to a similar degree. When 30 zircon crystals are sampled, the overlap of analytical performance between LA-ICP-MS and ID-TIMS is only present at very young ages (<1 Ma). This indicates that for the youngest systems, it may be possible to resolve a zircon age distribution using LA-ICP-MS where high-n_zircon datasets can be more easily acquired, though we emphasise that this requires further study since reported LA-ICP-MS uncertainties may be underestimated and often do not fully account for “matrix effects” (e.g. laser- and plasma-induced fractionation, reflected in 1 %–2 % long-term excess uncertainties) (Large et al., 2020; Sliwinski et al., 2022). With increasing age, the absolute precision of LA-ICP-MS decreases linearly, as evidenced by the rapid increase in misfit between 0 and ca. 100 Ma for n_zircon=30. For ages older than this, the misfit remains unchanged with increasing age because analytical uncertainties dominate the sampled distribution, forming a normal distribution. By contrast, for ID-TIMS, the misfit increases less rapidly with age. This continues until approximately 500 Ma, when the misfit is equivalent to LA-ICP-MS and the sampled dates form a normal distribution regardless of the shape of the underlying distribution.

4.4 Comparisons with thermal modelling of zircon age distributions

Zircon U–Pb age distributions provide the most robust time-resolved history of magmatic systems. Several studies have used these spectra in combination with thermal models to understand the dynamics of magma reservoirs, such as by quantifying the magmatic flux and the duration of magmatism (Caricchi et al., 2014; Tierney et al., 2016; Weber et al., 2020; Schmitt et al., 2023). Though initially such models assumed linear zircon crystallisation after zircon saturation (Caricchi et al., 2014, 2016), some recent models have taken into account the thermal and compositional dependence of zirconium solubility in a silicic melt and its effect on zircon saturation (Tierney et al., 2016; Schmitt et al., 2023). The generally older skew of plutonic age distributions observed in our analyses is consistent with that predicted from zircon solubility and thermodynamic models on a monotonically cooling magma reservoir (Watson, 1996; Keller et al., 2018, Fig. 7). However, thermal models that take into account incremental pluton assembly and heat transfer produce age distributions on a reservoir scale with young skew (e.g. Schmitt et al., 2023), which is at odds with our observation from natural plutonic rocks.

The discrepancy between natural plutonic age distributions (old skew) and thermal modelling of zircon age distributions (young skew) may be the result of several factors. Thermal modelling papers consider zircon age distributions at the reservoir scale, where slow cooling and heat transfer may delay the overall peak zircon crystallisation towards the solidus (young skew). However, the incremental assembly of such plutons may mean that on a localised scale relevant to that from which a hand sample may originate, the melt may cool rapidly and according to monotonic cooling and lead to older skew of zircon age distributions in a single sample. We note, however, that the >100 kyr durations of zircon crystallisation recorded by plutons may not be achieved by cooling of small melt batches, which could rather be explained by the bulk of zircon crystallising deeper than the emplacement level (Barboni et al., 2015; Nathwani et al., 2024). An additional factor is that a small number of datasets (Barboni et al., 2015; Samperton et al., 2015) contain fractured sub-grain analyses which can resolve intra-grain heterogeneity and thus better represent the true zircon crystallisation distribution (Klein and Eddy, 2023). For example, Samperton et al. (2015) present fractured sub-grain analyses where inner fragments show considerably older ages than external fragments (up to 500 kyr), which may explain the remarkable consistency of their age distributions with that predicted from zircon solubility and thermodynamics (Keller et al., 2018). However, old skew is observed in plutonic age distributions where sub-grain fragments were not analysed (e.g. Barboni et al., 2015; Kinney et al., 2021), suggesting it may not be a primary factor. Lastly, melt extraction from magma mush in the plutonic environment (e.g. to eruptions and dykes) may remove the youngest crystallised zircon, leading to a dominance of early crystallised zircon in the remaining intrusion. By contrast, zircons in volcanic rocks may represent the mixing of zircons crystallised throughout the entire magma reservoir, producing an age distribution more dominated by heat transfer (i.e. a younger skew).

Previous studies based on a more limited dataset have also noticed the young-skewed zircon age distributions in volcanic systems relative to plutonic systems (Caricchi et al., 2014; Tavazzani et al., 2023a). This has been used to suggest that volcanic systems have non-linear thermal histories and overall higher magma recharge rates (Caricchi et al., 2014; Tierney et al., 2016; Schmitt et al., 2023; Tavazzani et al., 2023a). However, our study indicates that these young-skewed zircon age spectra can also be produced by the truncation of zircon crystallisation by a volcanic eruption. Thus, we emphasise that decoupling the effects of recharge and truncation is challenging, and magmatic fluxes inverted from volcanic age distributions should be treated with caution, particularly when contrasted with plutonic age distributions. However, between plutonic systems (where truncation is not a large factor) it may be possible to more robustly quantify magma recharge rates using zircon age spectra. Future work on retrieving information on magma dynamics from zircon age spectra may therefore be best suited to younger plutonic systems (e.g. Barboni et al., 2015; Farina et al., 2024).

5 Conclusions

We provide a quantitative framework to compare high-precision zircon U–Pb age distributions of igneous samples using the Wasserstein distance and show that this statistical measure accurately captures differences in shape between age distributions. Our study provides a comprehensive analysis of a large database of CA-ID-TIMS data from 22 different magmatic systems. We filter our data compilation to isolate datasets where relative uncertainties permit the resolution of geological dispersion. The filtering approach includes a new method to systematically filter the tails of age distributions in large datasets. Exploring the effect of geological processes on age distributions is made challenging by varying ratios of zircon crystallisation duration to analytical precision ($\mathrm{\Delta }t/\mathit{\sigma }$) and varying numbers of sampled zircons. Notwithstanding these limitations, our analysis of natural data indicates clear geological differences between volcanic, porphyry and plutonic age distributions, where volcanic and porphyry zircon age distributions exhibit younger skew and plutonic exhibit older skew. We adopt a bootstrap modelling approach which generates synthetic distributions and permits comparison with natural distributions according to the Wasserstein distance. This analysis indicates that the younger skew of volcanic and porphyry age distributions can be best explained by variable degrees of truncation of zircon crystallisation by a volcanic eruption or porphyry dyke emplacement. We also show that magma recharge can contribute to the younger skew of volcanic and porphyry age distributions, though we suggest that the role of truncation is most important. This major control of zircon crystallisation truncation on an age distribution suggests that interpreting magma dynamics (e.g. quantifying magmatic fluxes) from volcanic age distributions may be challenging, and such an approach is more appropriate for plutonic age distributions. As analytical precision improves and increasing numbers and sizes of CA-ID-TIMS zircon U–Pb datasets are published, our framework will facilitate improved interpretation of geological information from zircon age distributions.

Appendix A: Symbols used in this study and their definitions

Symbol	Definition
Δt	Absolute duration of zircon crystallisation
Δtrel	Relative time between two zircon age distributions
ti	Time of crystallisation of ith zircon
trel	Relative time of zircon crystallisation
tsat	Time of initial zircon saturation
tend	Time of termination of zircon crystallisation
σ	Uncertainty
ECDF	Empirical cumulative distribution function
KDE	Kernel density estimation
${\widehat{F}}_n\left(t_{\mathrm{rel}}\right)$	Interpolated ECDF of age distribution
fxtal	Zircon age probability density function
Wp	The pth Wasserstein distance
nzircon	Number of zircon crystals
ninh	Number of inherited zircon crystals
δ	Delta function
d	Dissimilarity matrix
wi	Weighting of i
$\mathrm{\nabla }{\widehat{F}}_n\left(t_{\mathrm{rel}}\right)$	Gradient of interpolated ECDF
∇M	Gradient below which an ECDF is marked as discontinuous
tflat	Relative time of ECDF gradient below the gradient threshold
M−1	Inverse function of M