Further investigations into the accuracy of infrared radiofluorescence (IR-RF) and its inter-comparison with infrared photoluminescence (IRPL) dating

Infrared radiofluorescence (IR-RF) is an alternative dating technique for potassium feldspar grains, offering a higher signal stability and based on a simpler underlying mechanism than more common luminescence dating approaches. However, its accuracy when tested on known-age samples has so far shown inconsistent results. In this study, we present a refined accuracy assessment using samples that have previously produced unreliable IR-RF ages. Our approach incorporates two major methodological advancements developed over the past decade: elevated temperature measurements using the IR-RF₇₀ protocol and sensitivity change correction by vertical sliding. To expand the dose range comparison, we included two additional samples: one expected to be in saturation and another of modern age. Additionally, we evaluated the effect of using a narrower bandpass filter to exclude any signal contributions from potentially contaminating shorter wavelength emissions. Our results following the IR-RF₇₀ protocol with sensitivity corrections show an improvement over the original room-temperature results. For four out of the seven tested known-age samples spanning ca. 100–300 Gy (20–130 ka), we obtained results in keeping with the expected doses. Two additional modern samples, however, yielded slight dose underestimations. Introduction of a multiple-aliquot regenerative dose (MAR) protocol improved the accuracy of two out of three samples with large sensitivity changes. Finally, we also compared the new IR-RF equivalent doses (D_e) to those obtained with the newer dating method, infrared photoluminescence (IRPL), for the same samples, including previously published values and new measurements. Like IR-RF, IRPL is also expected to be trap-specific. We observe that, with the new improvements, the success rate of IR-RF is comparable to that of IRPL.

1 Introduction

Infrared radiofluorescence (IR-RF) dating of potassium (K)-feldspar is a technique used to determine the time since sediment deposition (e.g. Trautmann et al., 1998, 1999; Erfurt and Krbetschek, 2003b). The method consists of filling available electron traps within the mineral's crystal lattice through continuous ionising irradiation and quantifying the intensity of the resulting IR emission at ∼ 880 nm (this emission was previously reported at 865 nm; see Sect. 4.1 in Sontag-González et al., 2022). By comparing IR-RF curves obtained after natural burial with those obtained after a known laboratory dose (e.g. starting at zero dose following complete signal bleaching), the equivalent dose (D_e) accumulated since burial can be determined. Dividing the D_e by the sample's environmental dose rate yields the time since burial. The main advantages of IR-RF dating over the more common infrared stimulated luminescence (IRSL) of K-feldspar (Hütt et al., 1988) include a more athermally stable signal (based on IR-RF fading tests by Krbetschek et al. (2000) suggesting signal stability) and the large number of data points used to build the dose response curve (DRC).

Using a single-aliquot regenerative dose (IRSAR; Erfurt and Krbetschek, 2003a) protocol, Buylaert et al. (2012b) determined IR-RF ages for 16 coarse-grained K-feldspar samples and reported poor agreement with the independent age controls, which ranged from modern to ∼ 130 ka. For three modern samples, the IR-RF D_e values were shown to be highly sensitive to the bleaching method used between natural and regenerative measurements, with the most accurate results obtained using a solar simulator bleach of at least 4 h. The IR-RF ages of five young samples (∼ 100–150 Gy) were overestimated by ∼ 20 %–70 %, while those of eight older samples (∼ 200–300 Gy) were underestimated by ∼ 20 %–40 %. Over the past decade, significant methodological improvements in IR-RF dating have been developed, including measurement at 70 °C instead of at room temperature (Frouin et al., 2017) and a combination of horizontal and vertical sliding for D_e estimation (Kreutzer et al., 2017; Murari et al., 2018). The latter is intended to correct for reported sensitivity changes occurring between the two IR-RF measurements (e.g. Buylaert et al., 2012b; Varma et al., 2013). When introducing the IR-RF₇₀ protocol, Frouin et al. (2017) presented results for six samples, five of which matched the quartz-based ages (at 2σ). These new developments warrant a re-analysis of the previous findings on the accuracy of IR-RF ages reported by Buylaert et al. (2012b). Additionally, the segment of the natural dose curve used for D_e estimation with a vertical slide analysis needs to be systematically investigated. Previous work using only a horizontal slide has shown that the D_e is sensitive to the length of the natural dose curve used for sliding (Frouin et al., 2017). It is also conventional procedure to reject initial channels to avoid the “initial rise” effect, i.e. an unexpected signal increase at the beginning of natural and regenerative dose curves whose origin is not well understood (e.g. Buylaert et al., 2012b; Huot et al., 2015; Frouin et al., 2017). The initial rise has been shown to be dose-dependent (Frouin et al., 2017) and is avoided by removing up to a few tens of gray (Gy) from the beginning of the natural dose curve. However, the extent of its effect on the D_e is still not clear.

In parallel, Prasad et al. (2017) proposed a new dating method for K-feldspar based on IR photoluminescence (IRPL), which is relevant in the context of IR-RF dating. Both methods involve the emission stemming from electrons relaxing from the excited to the ground state of the K-feldspar principal trap. In IR-RF, these electrons originate from the valence band and get trapped during the process, whereas, in IRPL, the electrons are already trapped but are stimulated to the excited state with IR stimulation. Importantly, in IRPL, the electrons do not leave the trap, leading to a steady-state signal (i.e. electrons continuously “bouncing” between the excited and ground states of the principal trap during IR stimulation) and thereby representing a non-destructive measurement technique. Kumar et al. (2018) identified two IRPL emissions resulting from stimulation with an 830 nm laser, which are centred at 880 and 955 nm (IRPL₈₈₀ and IRPL₉₅₅, respectively). They also demonstrated that these two IRPL emissions correspond to the two known IR-RF emissions and suggested that they arise from the same defect (i.e. the principal trap) but with slightly different environments (i.e. neighbouring atoms or functional groups). The SAR IRPL protocol introduced by Kumar et al. (2021) also contains IRSL steps at increasing temperatures to sequentially target more stable traps, following the strategy of a multiple-elevated-temperature (MET) post-IR IRSL (pIRIR) protocol (Li and Li, 2011). Due to the non-destructive nature of IRPL, the inclusion of IRSL steps allows the comparison of several IRSL and IRPL signals for the same aliquots. Of the 11 sediment samples dated with IRPL (Kumar et al., 2021), 9 had also been dated using IR-RF by Buylaert et al. (2012b). They observed good agreement between the IRPL ages and the independent age controls for 8 samples ranging ∼ 100–300 Gy but obtained overestimated ages for 3 modern or very young samples. If the IRPL and IR-RF signals indeed originate from the same trap reservoir, they would be expected to yield similar D_e values, assuming there is no contamination from other emissions and negligible sensitivity changes during the measurement process. Kumar et al. (2021) observed poor agreement between their IRPL ages and IR-RF ages of the same samples reported by Buylaert et al. (2012b), which were obtained using room-temperature IR-RF measurements (IR-RF_RT) and without a correction for sensitivity changes. A comparison between IRPL measurements and the new improved IR-RF protocol (Frouin et al., 2017; Murari et al., 2018) is yet to be made.

In addition, the upper dating limits of both IR-RF and IRPL are still poorly understood. In the case of IR-RF, previous studies suggest the onset of saturation of the natural signal at around 1000 Gy. This value is based on measurements of a Triassic-age sample expected to be in saturation (Murari et al., 2021), measurements of a sequence of known-age samples from the Chinese Loess Plateau (Buchanan et al., 2022), and a study of long-term signal stability using artificially added gamma doses (Kreutzer et al., 2022a). These findings are at odds with the DRCs obtained in the laboratory, which continue to grow over > 3000 Gy. The upper dating limit of IRPL has not been studied using natural samples yet. However, the characteristic saturation dose (85 % saturation) of laboratory-irradiated DRCs ranges between ca. 1400 and 2500 Gy (Kumar et al., 2021) depending on the protocol used (e.g. with or without preheat). Comparison of the IRPL and IR-RF field saturation doses will help determine whether the relatively low upper limit of ∼ 1000 Gy for IR-RF dating is a characteristic of the principal trap or whether it is caused by issues specific to IR-RF. One potential issue is an overlap of the targeted IR-RF emission (centred at 880 nm) with a neighbouring red emission, which has been reported to be thermally unstable (Krbetschek et al., 2000). This overlap can be problematic for D_e estimation by making the natural dose curve not directly comparable to the regenerative dose curve, as the red signal would have already decayed in the natural sample but would still contribute to the total signal in the regenerated dose curve. Spectroscopic measurements of a field-saturated sample by Sontag-González and Fuchs (2022) reported differences in mean D_e of ∼ 400 Gy between integration of the ranges 810–850 and 850–890 nm, confirming that the detection window needs careful consideration. Shifting the detection window further into the IR reduces the contribution from the red emission, which we hypothesise would lead to more accurate D_e values.

Table 1 Details on sampling locations and previous dating studies. Uncertainties in the expected ages represent 1 standard error. IR-RF_RT refers to the room-temperature measurement protocol. Previous IR-RF_RT, IR-RF₇₀, and IRPL ages are given in Buylaert et al. (2012b), Murari et al. (2021), and Kumar et al. (2021), respectively.

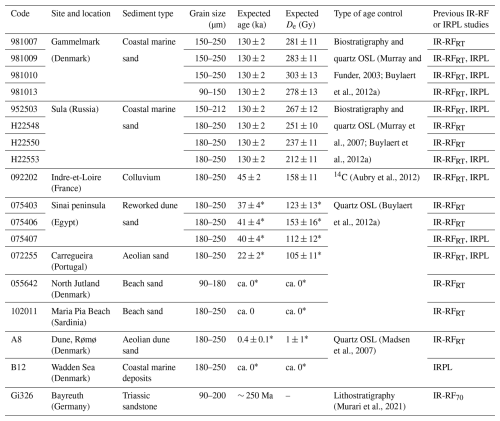
^∗Correction of 8.25 % to account for new source calibration (Autzen et al., 2022).

Here, we re-analyse the original IR-RF_RT data for the 16 samples with independent age controls dated by Buylaert et al. (2012b) to include a sensitivity change correction (vertical slide) and present new IR-RF D_e values obtained using the IR-RF₇₀ protocol for eight of these samples, which are expected to be more accurate. The IR-RF₇₀ dataset was then expanded by including one additional modern sample and one sample expected to be in field saturation (see Table 1 and Fig. S1 in the Supplement). We vary several IR-RF₇₀ measurement parameters to assess their effect on the resulting D_e in an effort to determine the combination that leads to the most accurate results. Tested parameters include the use of the vertical slide, the type of bleach between the natural and regenerative dose curve measurements, the number of rejected initial channels, the length of the natural dose curve used for sliding, and the detection window. On the basis of the SAR results, which suggest large sensitivity changes occur during the natural dose measurement for some samples, we also test the suitability of an IR-RF multiple-aliquot regenerative dose (MAR) protocol. Finally, we compare the IR-RF₇₀ results with MET pIRIR-IRPL ages for 10 samples. IRPL data of 7 of these samples have been published by Kumar et al. (2021), and we measured 3 new samples.

2 Samples and methods

2.1 Sample selection and preparation

A total of 18 samples (Table 1) were selected based on their independent age controls; 17 of these were prepared in the luminescence laboratory at Risø DTU following standard procedures. After initial wet-sieving, grain-size fractions of 90–150, 90–180, 150–212, 180–250, or 150–250 µm in diameter were treated with 10 % hydrogen chloride (HCl) and 10 % hydrogen peroxide (H₂O₂) solutions to remove carbonates and organic matter, respectively. K-feldspar grains were then isolated using a heavy liquid solution with a density of 2.58 g cm⁻³ and etched with hydrogen fluoride (HF; 10 %) for 40 min to remove the alpha-irradiated outer layer. A final HCl treatment dissolved any contaminating fluorides. One additional sample, Gi326, was prepared in the luminescence laboratory in Giessen, using the same chemical treatments, except for HF etching. This sample is from a Triassic sandstone and has been used previously to test the field saturation of IR-RF₇₀ (Murari et al., 2021).

Etching of K-feldspar has been reported to be uneven and sometimes lead to a larger volume removal than anticipated (Porat et al., 2015; Duval et al., 2018). The effect on the resulting D_e is poorly studied, but all samples expected to be in the dating range (i.e. not saturated) received the same treatment (HF etching), so any variation in D_e accuracy we observe for these samples would not be caused by a difference in sample preparation. Thus, we do not expect etching to affect our conclusions.

Due to a recently reported issue in past batches of the Risø calibration quartz (RCQ) commonly used to estimate the source dose rate (Tribolo et al., 2019), we adjusted the expected D_e of most samples. For the samples whose age controls were determined solely by quartz OSL (i.e. sample codes 075403, 075406, 075407, 072255, 055642, 102011, A8, and B12), we applied a correction factor of 1.0825 (Autzen et al., 2022). We note that, in the original publications of samples from Gammelmark (Denmark) and Sula (Russia), the quartz OSL ages were reported to underestimate the expected Eemian age by ca. 7 %–15 % (Murray and Funder, 2003; Murray et al., 2007). We interpret this observation as further support that the correction is necessary. For the eight samples from Gammelmark and Sula used here, we consider their expected ages to be 130 ± 2 ka (Murray and Funder, 2003; Murray et al., 2007), in contrast to the expected age of 128 ± 2 ka reported in Buylaert et al. (2012b), which presumably already accommodated the previous underestimated quartz OSL ages. The source dose rates for the data from Buylaert et al. (2012b) re-analysed here were also corrected by 1.0825.

2.2 Instrumental setup for IR-RF measurements

The original IR-RF_RT luminescence measurements from Buylaert et al. (2012b) were obtained using a Risø TL/OSL DA-20 reader (Bøtter-Jensen et al., 2010) with a specific attachment (Lapp et al., 2012), where the signal is transmitted through an optical light guide and filtered with a Chroma D900/100 interference filter before reaching a Hamamatsu H7421-50 photomultiplier tube (PMT). The effective detection window of this filter and PMT combination has a full width at half maximum (FWHM) spanning ∼ 850–875 nm. Large aliquots (∼ 8 mm), containing thousands of grains mounted on stainless-steel discs with silicone oil, were measured according to the IR-RF_RT protocol outlined in Table 2. Aliquots were bleached between the natural and regenerative dose steps using either built-in UV LEDs (395 nm) or an external SOL2 solar simulator (Hönle AG).

Table 2 IR-RF measurement protocols. “Natural dose” curve (step 2) refers to the RF measurement where an additive dose is administered on top of the natural dose. The length of the “regenerative dose” measurements (step 6) was sometimes shortened for younger samples.

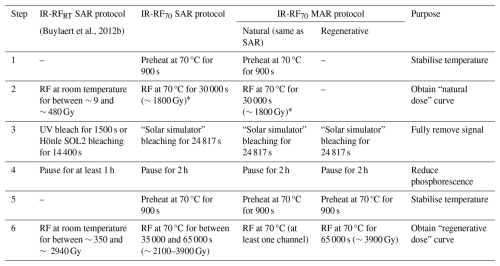
^∗ Only a segment of the natural dose curve was used for final D_e estimation; see Sect. 4.4.

New radiofluorescence measurements were performed at 70 °C (IR-RF₇₀) using a lexsyg research device (Freiberg Instruments GmbH; Richter et al., 2013) in Giessen (Germany) equipped with an annular beta source (⁹⁰Sr $/$ ⁹⁰Y) calibrated with a standard quartz sample using small aliquots on stainless-steel cups with silicone oil (RCQ batch 200; equivalent to 0.059 Gy s⁻¹ on 1 January 2023). We assume an uncertainty of 5 % for this calibration. Measurements in Sect. 3.2 were all conducted at the University of Oxford (UK) on the same type of device; further details can be found in Sontag-González et al. (2024). The calibrated annular beta source had a dose rate of 0.053 Gy s⁻¹ (1 January 2023). The radiofluorescence was filtered through a Chroma D850/40 interference filter before being detected by a Hamamatsu H7421-50 PMT with an effective detection FWHM spanning ∼ 825–860 nm. Additional experiments in Sect. 4.5 tested a different interference filter centred at 880 nm with an FWHM spanning ∼ 875–885 nm (Quantum Design 880HC10). Medium-sized aliquots (∼ 3–4 mm), containing hundreds of coarse grains, were mounted on stainless steel cups with silicone oil. For the “single-grain” measurements in Sect. 3.2, an individual grain was manually placed on each sample holder and fixed with silicone oil. The new measurements followed the IR-RF₇₀ protocol outlined in Table 2. Aliquots were bleached using a built-in LED-based solar simulator, according to the relative intensities in Frouin et al. (2015) and using the following power output: 365 nm (9 mW), 462 nm (55 mW), 525 nm (47 mW), 590 nm (32 mW), 625 nm (100 mW), and 850 nm (84 mW). In a separate bleaching test, some aliquots were bleached by direct sunlight exposure (see Sect. 4.3).

2.3 IR-RF data analysis

Data analysis of both the previous and the new IR-RF measurements was conducted in an R programming environment v4.0.2 (R Core Team, 2020). D_e values were obtained for each aliquot by sliding the “natural dose” curves onto the “regenerative dose” curves using either only a horizontal slide or both horizontal and vertical slides utilising the function “analyse_IRSAR.RF” from the “Luminescence” (v0.9.19) package (Kreutzer et al., 2012, 2022b). The IR-RF₇₀ curves from a representative aliquot are shown in Fig. 1, where the extent of vertical and horizontal sliding of the natural dose curve is shown as red bars. Sample D_e values were calculated using the arithmetic mean of the aliquot D_e values, and stated uncertainties are the standard error of the mean with the source calibration uncertainty added in quadrature. In the few cases in which the standard error was below the channel length (10 s, approximately 0.6 Gy), we regarded the channel length as the mean D_e uncertainty because that is the limit of our resolution. Example D_e distributions are shown in Fig. S2.

Figure 1 IR-RF₇₀ measurements of one aliquot of sample 092202 (position 23) before and after vertical and horizontal sliding of the natural dose curve (interference filter centred at 850 nm; FWHM of 40 nm). Note that the initial four channels (∼ 2 Gy) were not considered for the assessment of sliding quality. The D_e value determined for this aliquot is indicated on the x axis.

Following conventional procedure, the initial channels of each natural measurement were ignored during the analysis to account for the initial rise. The initial rise phenomenon is apparent in the first few data points of the curves shown in Fig. 1; in this case, removing the first channel of the natural dose curve would be sufficient to make the natural and regenerative dose curves comparable over the dose range of interest. We tested different rejection lengths, ignoring between 0 (no rejection) and ∼ 300 Gy of the initial part of the natural dose curve (i.e. removing between 0 and 499 channels). The effect of rejecting initial channels will be detailed in Sect. 4.4.

2.4 IRPL equipment and procedure

We measured the IRPL emissions centred at 880 and 955 nm for three samples using the same equipment as Kumar et al. (2021), including a ⁹⁰Sr $/$ ⁹⁰Y beta source calibrated using small RCQ aliquots on stainless-steel discs (equivalent to 0.19 Gy s⁻¹ on 1 January 2023). We used the IRPL attachment (Kook et al., 2018) to the Risø TL/OSL reader with two photomultiplier tubes: a Hamamatsu H10330C-25 in combination with a bandpass interference filter centred at 950 (FWHM of 50 nm) for the IRPL₉₅₅ emission and a Hamamatsu H7421-50 in combination with either a bandpass interference filter centred at 880 nm (FWHM of 10 nm) for the IRPL₈₈₀ or BG39 and BG3 filters for the IRSL emission. IR LEDs (850 nm with a power density of ∼ 250 mW cm⁻² at sample position) were used as the stimulation for IRSL. The IRPL stimulation consisted of an external laser light source (830 nm with a power density of ∼ 3 mW cm⁻² at sample position) in a pulsed excitation mode (50 µs on-time followed by 50 µs off-time) for 5 s. IRPL was only measured during the off-time, rejecting the first 3 µs to avoid contamination by the excitation source (PMT gate 53–100 µm).

The measurement protocol consists of an MET pIRIR protocol based on Protocol A of Kumar et al. (2021) and using IR stimulation temperatures of 50, 90, 130, and 290 °C (IRSL₅₀, pIRIR₉₀, pIRIR₁₃₀, and pIRIR₂₉₀, respectively) with room-temperature IRPL measurements interspersed between each step (Table S1). The preheat step was set to 320 °C (60 s), and the IR stimulation at 290 °C (100 s) was used to remove residual signal prior to each irradiation step (cleanout). IRPL signals for each emission were calculated as the integral of the 5 s long measurements, subtracting as background the residual IRPL obtained after the 290 °C IR cleanout (step 16 or 17 in Table S1 for IRPL₈₈₀ or IRPL₉₅₅, respectively). Figures S3 and S4 show examples of the IRPL curves used to obtain the signal and background, respectively. Figure S5 displays examples of the resulting DRC. IRSL signals were also determined for comparison, consisting of the integral of the first 2 s with the last 10 s used for background subtraction. Sensitivity change corrections for IRSL and IRPL consisted of dividing the signal obtained from the natural or various doses (L_n or L_x, respectively) by that obtained from a test dose (T_n or T_x) for each SAR cycle. The IRPL and IRSL DRCs were fitted with double exponential functions for better comparability with Kumar et al. (2021). Aliquots were only considered for D_e estimation if they passed the following criteria: minimum signal brightness (T_n more than three sigma of the background level and a relative standard error of T_n < 10 %), reproducibility (recycling ratio within 10 % of unity), and low signal carry-over (recuperation < 15 %).

3 Considerations on the IR-RF DRC

Among other parameters, in Sect. 4, we will investigate the segment of the natural dose curve that should be used for D_e estimation with a vertical slide analysis. In theory, if the natural and regenerative dose curves have the same signal components and follow the same decay, we would not expect any difference in D_e values from natural dose curves of different length, provided the segment is long enough for a statistically reliable slide. We can test this hypothesis by measuring a long natural dose curve for all aliquots and repeating the D_e analysis using segments of different lengths. Two parameters can be changed in this analysis: the start and end channels of the natural dose curve segment to be used for sliding. Naturally, not every combination makes sense, so here we summarise past studies and preliminary analyses to inform on the combinations we should focus on.

3.1 Initial signal rise: removing initial channels

The segment of the natural dose curve visibly affected by the initial signal rise is often avoided for dating. For example, Buylaert et al. (2012b) removed between 1 and 33 Gy from the start of the curve. Frouin et al. (2017) reported a dose dependence of the initial rise, with the peak maximum ranging from ∼ 2 to ∼ 40 Gy for samples with D_e values of 0 to ∼ 300 Gy. Similar values were reported by Murari et al. (2021): ∼ 3 and ∼ 20 Gy for a modern sample and a saturated sample, respectively. Thus, removal of up to the initial ∼ 40 Gy appears to be warranted.

3.2 Initial signal rise: insights from single grains

Previous research has suggested differences in IR-RF characteristics at the single-grain level which would be averaged in the multi-grain aliquots used in the present work (Trautmann et al., 2000; Frouin et al., 2017; Mittelstraß and Kreutzer, 2021). For example, our earlier work on sample H22550 (Sontag-González et al., 2024) revealed that only three out of six measured grains produced the expected IR-RF signal (i.e. decreasing with dose, referred to as Type #1). One additional grain exhibited an initial signal rise followed by signal saturation at ∼ 100 Gy (termed Type #2). The remaining two grains showed a flat signal shape indistinguishable from that of an empty sample holder. These results suggest potential issues for IR-RF multi-grain measurements. By mathematically adding the IR-RF signal (i.e. a synthetic aliquot) obtained from individual grains of sample H22550 by Sontag-González et al. (2024), we modelled the signal from multi-grain aliquots with different proportions of the two grain types (Fig. 2). If at least one-third of the grains in a multi-grain aliquot yield the expected IR-RF signal, they will dominate the total signal, and, overall, the signal shape will follow the Type #1 grain pattern (Fig. 2, inset). Interestingly, our modelled signal displays an “initial signal rise” which decreases with a decrease in the proportion of unwanted Type #2 grains. This suggests that (i) the “initial signal rise” originates from signal contamination by presumably non-K-feldspar minerals and that (ii) the DRC of the modelled “contaminated” aliquot converges with that of the “pure” one (for this sample at ∼ 100 Gy). This observation suggests we should investigate removing a larger portion of the initial curve than previously expected.

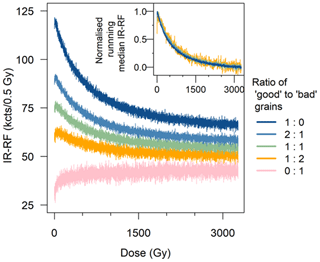
Figure 2 Simulation of regenerative dose IR-RF₇₀ curves of aliquots of sample H22550 composed of a combination of grains with the expected IR-RF signal shape (“good” grains, Type #1) and grains with an initially increasing signal shape (“bad” grains, Type #2). The “good” grain curve (dark blue) is the average of three individual grains with the expected signal shape, whereas the “bad” grain curve was obtained from one grain. The grains are referred to as ID #3, #4, #5, and #6 in Sontag-González et al. (2024). The inset shows the same curves (except for that composed entirely of Type #2 grains) normalised to their maximum signal values, removing as background the median value of the last 100 channels (∼ 60 Gy). Note the decrease in “initial rise” with increasing proportion of “good” grains relative to the total dynamic signal range.

3.3 Length of natural dose curve segment

Frouin et al. (2017) conducted an iterative test increasing the segment length over the first 100 channels (horizontal slide) and found that, for their samples, a D_e plateau was reached after ∼ 40 channels (∼ 30 Gy with their 0.7 Gy per channel). In Buylaert et al. (2012b), the natural dose curve length varied between 5 and 475 Gy, depending on the sample. More recent studies are showing a preference for the use of long natural dose curves of ∼ 260 Gy (Key et al., 2022) or 500–600 Gy (Murari et al., 2021; Scerri et al., 2021; Kreutzer et al., 2022a; Buchanan et al., 2022, 2024).

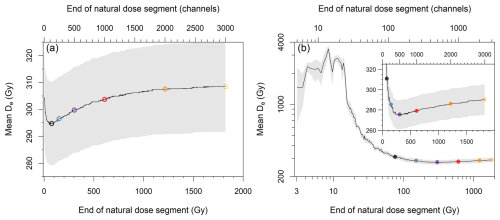
Figure 3 Representative example of the effect of the length of the natural dose curve on the mean D_e for sample 981009 with an IR-RF₇₀ protocol (mean of three aliquots). The segment length was iteratively increased by one channel, and D_e values were estimated using (a) a horizontal slide or (b) a vertical and a horizontal slide. The initial ∼ 2 Gy (four channels) was always rejected. Note that the main plot in panel (b) is shown in logarithmic scale. The inset shows a magnification of the region of interest of the main plot. The grey shading represents the standard error of the mean. The coloured points indicate the segment lengths chosen for further analysis.

For a preliminary analysis, we tested the effect of varying the natural dose curve segment for one sample (981009). Having measured long curves of ∼ 1800 Gy, we obtained 2996 mean D_e values using incrementally larger segments (Fig. 3), having removed the initial ∼ 2 Gy (4 channels) in all iterations. When using the vertical and horizontal analysis, a large change in D_e values was observed (Fig. 3b), but no D_e plateau was reached. Short segments (< 15 Gy) led to unrealistically high D_e values of thousands of gray possibly due to the uncertainties of the sliding algorithm, so we will focus on larger curve segments. Six representative segment lengths of between ca. 75 and 1800 Gy were chosen to cover the range expected to yield reliable results for dating. We also note that the pattern of D_e variation based on sliding segment appears to be a dose-dependent characteristic (see Fig. S6). Thus, the choice of segment should account for the differences in source dose rate of different readers; i.e. the choice should be made based on dose rather than number of channels.

4 IR-RF D_e estimation

4.1 Effect of vertical slide correction

The original mean D_e values obtained by Buylaert et al. (2012b) using an IR-RF_RT protocol are reproduced in Fig. 4a (open circles). When using the internal UV LEDs for the bleaching steps between the natural and regenerative dose steps, the D_e values are either over- or underestimated (at 2σ) for all 16 samples. By replacing the UV bleaching step with an external bleach in a solar simulator (SOL2) for a subset of six samples, Buylaert et al. (2012b) observed an improvement in results, but the D_e values were still under- or overestimated for five of the six samples tested (Fig. 4a, open squares).

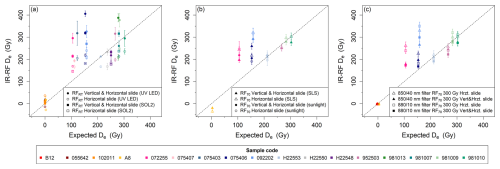
Figure 4 Comparison of published and new IR-RF results with the expected D_e values. (a) IR-RF was measured at room temperature (RT). The measurements from Buylaert et al. (2012b) (open symbols) were analysed without vertical slide. Those measurements were re-analysed here with vertical slide correction of sensitivity changes (filled symbols). Aliquots were bleached with UV LEDs or an external solar simulator (SOL2) between the natural and regenerative dose measurements. (b) IR-RF of a subset of the same samples as in the previous panel measured at 70 °C. D_e values were obtained with (filled symbols) and without (open symbols) vertical slide. The same natural dose segments as in Buylaert et al. (2012b) were used for sliding. Aliquots were bleached with the internal solar simulator made up of an LED array (SLS; nine samples) or direct sunlight (four samples) between the natural and regenerative dose measurements. (c) All IR-RF₇₀ with different detection filters using a segment of the natural dose curve spanning ∼ 300 Gy (500 channels) but rejecting the initial ∼ 2 Gy (4 channels). Note that a 5 Gy interval was placed between the expected doses of the modern samples to aid visualisation.

Table 3 Results from IR-RF measurements at room temperature (RT), either with or without sensitivity change correction. Data have been re-analysed from Buylaert et al. (2012b). Aliquots were bleached with UV LEDs or an external solar simulator (SOL2) between the natural and regenerative dose steps. “n” refers to the number of aliquots used to determine the arithmetic mean D_e. IR-RF D_e uncertainties represent the standard error.

Application of the new vertical slide correction for sensitivity changes led to an increase in D_e values for all samples except for one of the modern ones (Table 3 and Fig. 4a, filled symbols). This adjustment resulted in eight samples aligning with the expected D_e (at 2σ), but it also increased the overestimation for most of the other samples. A similar pattern was observed for the aliquots bleached with UV LEDs and with SOL2. For the UV LED dataset, the sensitivity change correction led to an increase in the scatter of the D_e distribution of most samples, evident from the increased standard errors of the mean (Fig. 4a). These results suggest that sensitivity change corrections alone do not improve the accuracy of IR-RF_RT results.

4.2 Effect of measurement temperature

Of the 16 samples analysed in Sect. 4.1, we selected 8 for new measurements at 70 °C, keeping only 1–2 samples per site. The new measurements using the IR-RF₇₀ protocol showed a better agreement with the expected values (Fig. 4b). Four of the samples have D_e values matching expectations at 1σ. Interestingly, for these four samples, results with and without the sensitivity change correction were indistinguishable from each other at 1σ.

For all aliquots, we measured the natural dose curves over a relatively long dose range of ∼ 1800 Gy when using the IR-RF₇₀ protocol. However, for the results shown in Fig. 4a–b, we used the same dose ranges in the sliding procedure as in the original analysis of Buylaert et al. (2012b) to allow a more direct comparison. We adjusted the total lengths of the natural dose curve segments (5–475 Gy) and removed the initial channels (1–33 Gy) aliquot-wise.

4.3 Effect of bleaching type

Given the large differences in IR-RF D_e observed by Buylaert et al. (2012b) when using the internal UV LEDs or an external solar simulator (SOL2) for the signal bleach between the natural and regenerative dose steps, we tested the efficacy of the internal solar simulator for IR-RF₇₀ measurements by comparing it to a solar bleach. We used three samples with poor matches to their expected doses (sample nos. 092202, 075406, and 072255) and one sample that matched its expected dose (H22553). Three aliquots per sample received an external solar bleach between the natural and regenerative steps by placing them on a windowsill for 1 week in late May in Giessen, Germany. The aliquots were exposed to a cumulative ∼ 82 h of daylight, including at least 8 h of direct sunlight. For three of the four samples, D_e values obtained with vertical slide correction were statistically indistinguishable (at 1σ) from those obtained using the internal solar simulator (Fig. 4b), suggesting that the type of bleaching may contribute to the inaccuracy of some samples but is not the main cause behind it.

4.4 Sliding range of IR-RF₇₀ natural dose curve

Now, we will investigate how the choice of the natural dose curve segment used for sliding affects the resulting D_e value with the IR-RF₇₀ protocol following the considerations laid out in Sect. 3. For the following, we added two new samples to the dataset, which were not analysed by Buylaert et al. (2012b): a modern sample (B12) and a field-saturated sample (Gi326). At least three aliquots were measured per sample.

Figure 5 Comparison of IR-RF₇₀ mean D_e values using fixed segments of the natural dose curve and (a, c, e, g, i) only horizontal sliding or (b, d, f, h, j) vertical and horizontal sliding. For clarity, the used segments of a representative natural dose curve (sample 092202) are shown in the legend box to the right of the corresponding plots. Note that a 5 Gy interval was placed between the expected doses of the two modern samples to aid visualisation. The D_e for the field-saturated sample Gi326 is shown on the right-hand y axis in each plot; its expected D_e is “saturated” (sat.). The dashed line indicates the 1 : 1 line. (e, g) Arrows indicate a minimum estimate caused by the limit of the regenerative dose curve.

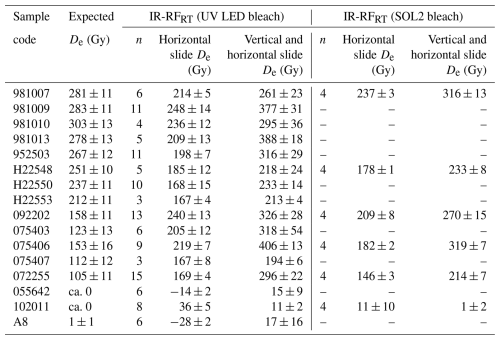
Firstly, we assessed the dose range that should be removed from the beginning of the natural dose curves to mitigate the initial rise effect. We compared the mean D_e values resulting from using the initial ∼ 150 Gy of the natural dose curve, while rejecting various initial amounts: 0 (no rejection), 2, 5, 11, 17, 36, or 72 Gy for each of 10 samples (Fig. 5a–b). Note that the rejected channels are still considered for D_e calculation to be a laboratory-added dose even though they are excluded from the sliding algorithm to assess goodness of fit. Using only a horizontal slide analysis (Fig. 5a), we observed no significant change in D_e except for the modern samples, for which only the iterations without any rejection matched the expected doses. When applying the sensitivity change correction (Fig. 5b), we observed a pattern of gradual decrease in D_e values of up to 17 % (relative to the no rejection scenario) for all non-modern samples.

We then repeated this test using longer segments of the natural dose curve (∼ 300 or ∼ 600 Gy) while rejecting the initial 0–150 or 0–301 Gy for each of the 10 samples (Fig. 5c–d and e–f, respectively). Similar patterns to those with the short segment were observed but with a smaller gradual change in D_e with increasing segment length for the non-modern samples (up to 10 % and 11 % relative to the no-rejection scenario, respectively). Comparing results from natural dose curve segments of different lengths (∼ 150, 300, or 600 Gy) with sensitivity change correction (Fig. 5b, d and 3f, respectively) reveals that the length of the segment has a higher impact on D_e than the amount of rejected initial channels. If the natural dose curve is sufficiently long, up to ∼ 35–100 Gy can be removed to address the initial rise effect.

However, the question remains as to how long the natural dose curve should be. We tested this by fixing the beginning of the curve (rejecting the initial 2 Gy to avoid the channels most affected by the initial rise) and changing the length of the curve to span ∼ 75, 150, 300, 600, 1200, or 1800 Gy, i.e. 125, 250, 500, 1000, 2000, or 3000 channels, respectively (Fig. 5g–h). For the two modern samples, we observed minimal D_e variation. For the other samples and without a sensitivity change correction, we observed a gradual increase in D_e with increasing length of the natural dose curve (Fig. 5g). Relative to the shortest segment (∼ 75 Gy), the D_e values increase by between 3 % and 27 %, with the larger increases (15 %–27 %) observed for the field-saturated sample and for the three samples with poor matches to the expected doses. Note that, for the field-saturated sample, the longest segment yielded only a minimum dose estimate due to the limit of the regenerative dose curve (i.e. the analysis algorithm restricts sliding the natural dose curve further than the end of the regenerative dose curve). The remaining four samples showed only 3 %–5 % increase. We observed a similar pattern when applying the sensitivity change correction, but the trend of increase in D_e generally begins only for segments > 300 Gy, and it is superimposed onto an initial D_e decrease (see also Fig. 2b).

The results shown in Fig. 5g–h suggest sensitivity changes occur during measurement of the natural dose curve that are not corrected by vertical sliding, as this method only addresses changes between the end of the natural dose curves and the beginning of the regenerative dose curves. A comparison of the fit quality between the natural dose curves and the regenerative dose curves for samples with small and large sensitivity changes is shown in Fig. S7.

To further investigate sensitivity changes, we repeated the D_e estimations for all samples using segments of the natural dose curves spanning ∼ 300 Gy but beginning at either 2, 301, 602, 903, 1205, or 1506 Gy (Fig. 5i–j). We observed a gradual change in D_e for all samples with both analysis types. Without a sensitivity change correction, D_e values increased by up to 22 %–294 % (relative to the initial segment) for the non-modern samples. The three samples whose D_e values consistently overestimate (sample nos. 092202, 075406, and 072255) had much larger increases (78 %–294 %) than the four other non-modern samples (22 %–36 %). The modern samples had either an increase or a decrease of 60–75 Gy. For the field-saturated sample, the final three segments yielded only a minimum dose estimate due to the limit of the regenerative dose curve. We observed a D_e increase of up to 32 % for the field-saturated sample but expect that this number would be higher if the regenerative dose curve had been longer and thus allowed an absolute value for the final three segments. With the sensitivity change correction, the D_e increases were less pronounced: up to 49 %–116 % for the three “problematic” samples and for the field-saturated sample and up to 12 %–28 % for the other non-modern samples.

Table 4 Results from IR-RF measurements at 70 °C using different bandpass filters and IRPL measurements after the preheat step (APh) and after the IRSL₅₀ step (pIR₅₀IRPL). IR-RF D_e values were obtained using either a single- or multiple-aliquot regenerative dose (SAR or MAR, respectively) procedure. SAR IR-RF D_e values were obtained using the initial ∼ 300 Gy (500 channels) of the natural dose curve, rejecting the initial ∼ 2 Gy (4 channels) and applying a sensitivity change correction (horizontal and vertical slide), whereas MAR D_e values were obtained from segments of the natural dose curve spanning ca. 108–1808 Gy (180–3000 channels). “n” refers to the number of aliquots used to determine the arithmetic mean D_e. IR-RF D_e uncertainties represent the standard error.

^∗ IRPL results taken from Kumar et al. (2021).

Overall, the length of the natural dose curve segment used for sliding affects the resulting D_e values for most of the tested samples. For short segments (e.g. ≤ 151 Gy), results using the vertical slide analysis are very sensitive to an initial channel rejection. Excessively long segments might lead to a dose overestimation possibly due to sensitivity changes occurring during the natural dose curve measurement. A segment of ∼ 300 Gy seems to be relatively insensitive to the rejection of the initial channels for non-modern samples and avoids the D_e increase observed for longer segments. Mean D_e values for all samples using this segment are given in Table 4 and shown in Fig. 4c (see Fig. S2 for the D_e distributions).

4.5 Detection window

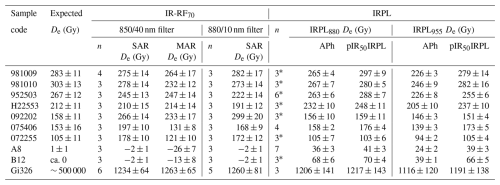
The observed dose-dependent mismatch between the natural and the regenerative dose curves could be due to varying contributions from neighbouring emissions to the total signal. To test whether the observed D_e variations are caused by a contribution of the red RF emission (centred at ca. 700–730 nm; Trautmann et al., 1998; Krbetschek et al., 2000), we shifted the detection window further into the IR by replacing the bandpass filter centred at 850 nm (FWHM: 40 nm) with one centred at 880 nm (FWHM: 10 nm) and repeating all measurements (three aliquots per sample) and analyses discussed in Sect. 4.4. We chose a filter with a narrower detection window to avoid emissions in shorter or longer wavelengths than the desired 880 nm RF emission. If the red emission contributed to the total signal, we would expect a higher D_e accuracy and lower D_e variations with segment choice when using the new filter.

Measurements with the 880 nm filter showed slightly more variability, probably due to the lower signal intensity with the narrower filter (compare Figs. S7 and S8). However, we generally observed similar patterns with both filters. The mean D_e values are statistically indistinguishable (at 2σ) for 9 of the 10 samples. An overview of the results for all tested natural dose segments is shown in Fig. S9. The mean IR-RF₇₀ D_e values for all samples using the initial ∼  300 Gy segments are given in Table 4 and compared with those using the broader filter in Fig. 4c (the results for sample Gi326 will be discussed in Sect. 7).

5 An IR-RF MAR protocol

As indicated in Sect. 4.4, some samples appear to suffer from significant progressive sensitivity changes during the first laboratory irradiation, thereby making the natural and regenerative dose curves not directly comparable. More importantly, the vertical slide is not an effective technique to correct for such progressive sensitivity changes, as it only corrects for changes in signal intensity but still assumes that the curve shapes are comparable. In luminescence dating, MAR procedures (Aitken, 1998) can be implemented to circumvent sensitivity changes when the typical test dose correction in a SAR protocol is deemed insufficient for either quartz (e.g. Lu et al., 2007; Ankjærgaard, 2019) or K-feldspar applications (e.g. Li et al., 2013). In MAR protocols, the natural and regenerative datasets stem from different aliquots, with the latter being bleached to remove the natural signal prior to a laboratory irradiation.

We tested the suitability of an IR-RF MAR protocol to overcome the sensitivity changes induced by the first laboratory irradiation of an aliquot. The protocol consisted of obtaining the natural dose curves for several aliquots following the same steps as in a SAR protocol (for simplification, the same dataset was used as in Sect. 4.4), whereas the regenerative dose curves (one per sample) were obtained from new aliquots in which the natural dose curve step and associated preheat were skipped (MAR protocol in Table 2). To account for inter-aliquot differences in mass and signal intensity, each SAR natural dose curve was scaled by the ratio between the first data point of the MAR and SAR curves, as exemplified in Fig. S10. An instrumental background was subtracted from each curve prior to normalisation, using the mean signal intensity of a 1000 s long measurement of an empty sample holder (12 961 cts per channel).

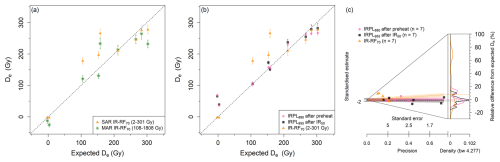
Figure 6 Comparison of the new IR-RF₇₀ and IRPL results with the expected D_e values. (a) Single-aliquot regenerative dose (SAR) IR-RF₇₀ results and those obtained using a multiple aliquot regenerative dose (MAR) protocol. Results are shown for the most reliable natural dose curve segment of each protocol, as given in the legend. (b) IRPL and SAR IR-RF₇₀ are measured on the same set of samples. The IRPL D_e measurements are a combination of new measurements and those from Kumar et al. (2021). The subscript after “IRPL” in the legend indicates the wavelength of the targeted emission. IR-RF₇₀ D_e values were obtained with vertical and horizontal slide. Note that a 5 Gy interval was placed between the expected doses of the modern samples to aid visualisation. (c) Abanico plot of the distributions of the relative differences from the expected D_e values (using only the non-modern samples).

We repeated the MAR D_e analysis using varying natural dose curve segments, as previously described for the SAR protocol in Sect. 4.4. As shown in Fig. S11, the use of different segments led to different D_e values for all 10 investigated samples, though some differences in pattern are of note. Unlike the SAR analysis, in which use of an increasingly long natural dose curve segment led to higher D_e values for all samples (Fig. 5h), with the MAR analysis, increasingly long segments (i.e. 2−151 to 2−1808 Gy) led to a better agreement with expected D_e values for five non-modern samples and very small changes for the remaining four samples of known age (Fig. S11d). For this reason, we also considered how many channels should be removed from the beginning of the 1808 Gy long natural dose curve (Fig. S11c). We found that rejecting the initial 108 Gy was the best compromise to achieve a good agreement with expected D_e values across the non-modern samples (Fig. 6a and Table 4). The MAR protocol using a natural dose curve segment of 108–1808 Gy (180–3000 channels) with vertical and horizontal slide yielded D_e in agreement with the expected values (at 2σ) for five out of the seven non-modern samples of known age, including for two of the three samples identified as “problematic” in Sect. 4.4.

6 Comparison of IR-RF and IRPL

A subset of the samples used in Sect. 4 to evaluate different IR-RF protocols have also been used to assess the accuracy of IRPL (Kumar et al., 2021), allowing us to directly compare both methods. To create a more comprehensive dataset, we measured three additional samples (075406, A8, and Gi326) following an IRPL protocol and using the same equipment as Kumar et al. (2021). For each sample, between three and seven aliquots were measured.

Since the IRPL signal measurement is mostly non-destructive, it can be taken at several steps in the protocol, yielding several IRPL D_e values for each emission (i.e. both before and after the preheat and after each IRSL step). Note that the IRPL steps after the IRSL₂₉₀ step are merely used to determine a background signal (see Fig. S4) and do not yield a D_e value. In this study, we measured the 880 nm and the 955 nm IRPL emissions. The sequential IRSL steps can also each be used to obtain a D_e value, thus resulting in a total of 14 D_e values for each aliquot (see Table S1).

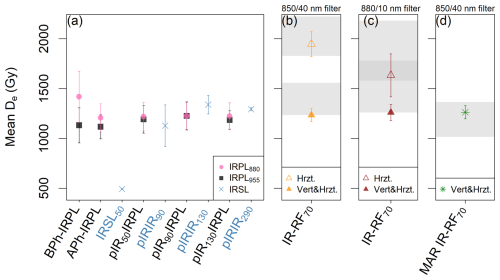
Figure 7 Comparison at field saturation for sample Gi326. (a) Mean D_e values obtained from the various steps in the IRPL sequence, including the IRSL steps (highlighted in blue in the x-axis labels). “BPh” and “APh” refer to before and after the preheat step, respectively. The IR-RF mean D_e values were obtained using (b, d) an 850/40 nm and (c) an 880/10 nm bandpass filter. (b, c) The initial ∼ 300 Gy segment of the natural dose curve (rejecting the first ∼ 2 Gy) was used with horizontal or with vertical and horizontal sliding (Hrzt. and Vert&Hrzt., respectively). (d) Results obtained using a multiple-aliquot regenerative dose (MAR) protocol and sliding the natural dose curve segment spanning 108–1808 Gy. The range of D_e values that could be obtained using alternative natural dose curve segments (i.e. those in (b) Fig. 5g–h, (c) Fig. S9g–h, and (d) Fig. S11b–d) are shown as grey bands without the associated uncertainties.

The mean D_e value for each IRPL signal of the field-saturated sample Gi326 is shown in Fig. 7a. With the exception of the IRSL₅₀ D_e, which is expected to be significantly affected by fading, all other D_e values are similar, ranging from ∼ 1100 to ∼ 1400 Gy. After the IRSL₅₀ step, we observed a convergence of the different IRPL signals to ∼ 1200 Gy. This value is slightly lower than the pIRIR₂₉₀ mean D_e value at 1293 ± 14 Gy (Fig. 7a) and the IR-RF mean sensitivity change-corrected D_e values, which are also at ∼ 1300 Gy (Fig. 7b–d). We do not notice a significant change between the pIR₅₀IRPL and the following IRPL mean D_e values, suggesting there is no sequential removal of unstable IRPL signal after increasingly hot IRSL steps beyond 50 °C for this sample. A similar behaviour is observed for the three pIRIR mean D_e values, though the large uncertainties in the pIRIR₉₀ and pIRIR₁₃₀ mean D_e values might obscure the expected step-wise increase in signal stability with increasing IRSL temperature (e.g. Li et al., 2013).

Kumar et al. (2021) stated that the IRPL₈₈₀ after the preheat step (APh-IRPL₈₈₀) and the pIR₅₀IRPL₉₅₅ signals are the most promising ones for sediment dating, based on a better agreement with the expected doses. Mean D_e values for these two signals, including two new samples, are shown in Fig. 6b together with the most promising IR-RF signal. The values for other IRPL signals are shown in Fig. S12 (new samples) and Fig. S13 (all samples). The mean D_e values from the pIR₅₀IRPL₉₅₅ signal in Fig. 6b are in good agreement (at 2σ) with the expected doses for all non-modern samples and for six out of seven samples using the APh-IRPL₈₈₀ signal, including two samples strongly overestimated with IR-RF₇₀. However, IR-RF₇₀ is in much better agreement than any of the IRPL signals for the two modern samples. See Fig. S14 for a direct comparison of the IR-RF and IRPL D_e values.

7 DRC shape and signal saturation

The results presented in Sect. 4 showed variability in the IR-RF₇₀ signal across samples regarding their potential to yield the expected dose and the purported sensitivity changes occurring during the natural dose curve measurement. To assess the variability in the IR-RF curve shapes, we plotted all curves obtained with the 850 nm bandpass filter (FWHM: 40 nm) in Fig. 8. In the natural dose curves (Fig. 8a), the modern and field-saturated samples are distinguishable by their steeper and flatter shapes, respectively (highlighted in pink and grey, respectively). The regenerative dose curves (Fig. 8b) show sample-dependent variability in signal brightness and in the “background” level after ∼ 4000 Gy. However, after subtracting the signal value at 1800 Gy as background and normalising the natural dose curves to the signal value at 3 Gy (to discount patterns caused by the initial signal rise), the natural DRC shapes of all samples are relatively similar (Fig. 8a, inset), with small differences observed for the field-saturated and modern samples and for samples 092202 and 075406. In contrast, an equivalent analysis of the regenerative dose curves yielded larger differences in DRC shape (Fig. 8b, inset). All samples follow a similar pattern, except for samples 092202 and 075406 (highlighted in blue and orange in Fig. 8), which saturate later and earlier than the other eight samples, respectively. These two samples were also identified as problematic in Sect. 4.4 when using different segments of the natural dose curve for sliding. An early-saturating DRC could potentially explain gradually more inaccurate D_e values (as observed in Fig. 5i–j) due to the higher uncertainties when using a flatter curve for sliding (i.e. near-saturation). However, the same behaviour of gradually higher overestimation was observed for sample 092202, with a late-saturating curve, and for sample 072255, whose curve shape follows the consensus. Thus, variability in saturation behaviour does not seem to be the root cause of the observed D_e inaccuracy. The DRC shapes of the MAR (in Fig. 8c) follow the same overall pattern across samples as the regenerative dose SAR curves.

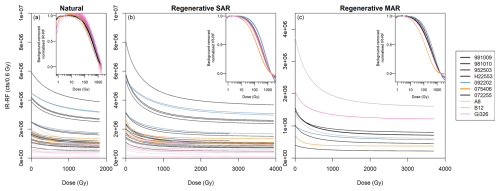
Figure 8 IR-RF DRC shape comparison of (a) the natural dose signal, (b) the regenerative dose signal using a SAR, and (c) the regenerative dose signal using a MAR protocol, all measured with an 850 nm bandpass filter (FWHM: 40 nm). In the insets, a background was subtracted from the IR-RF curves, corresponding to the signal value at a dose of 1800 Gy before normalisation to the signal value at 3 Gy. Curves from the two modern samples and the field-saturated sample are shown in pink and grey, respectively. The DRCs of two additional samples are coloured to highlight their deviation from the curve shape of all other samples.

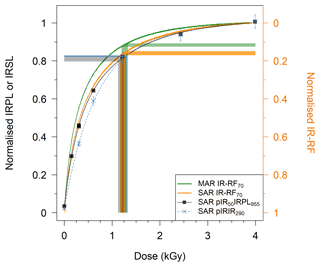
Figure 9 DRC shape comparison of representative aliquots of Gi326. The pIR₅₀IRPL₉₅₅ and pIR₉₀IR₂₉₀ curves are double exponential functions fitted to the sensitivity-corrected signals ($L_x/T_x$) of 7–8 regenerative doses each, including a repeated dose point (∼ 300 Gy). All curves were normalised to their maximum values. Before normalisation, a background was subtracted from the IR-RF curves, corresponding to the median value of the last 100 channels (∼ 60 Gy). The IR-RF curves decrease with dose, so they were plotted on an inverted axis (right-hand side) to allow a direct comparison. The shaded regions indicate the 1σ range around the four mean D_e values and their projection onto the corresponding DRC.

We also compared the IR-RF₇₀, IR-IRPL, and pIRIR DRC shapes up to ∼ 4000 Gy for representative aliquots of the field-saturated sample Gi326 (Fig. 9). Note that only the pIR₅₀IRPL₉₅₅ signal is shown in Fig. 9, but all IRPL signals measured after the preheat step have very similar DRC shapes (see Fig. S5). Likewise, the IR-RF₇₀ DRCs of sample Gi326 measured with an 880 nm (FWHM: 10 nm) or 850 nm (40 nm) bandpass filter are very similar in shape (compare Figs. S7 and S8). By plotting the regenerative IR-RF curves onto an inverted axis, we could directly compare their shapes to those of the other signals, despite their decrease with increasing dose. To assess only the dynamic range of the IR-RF curve, we accounted for the high background signal typical of IR-RF by subtracting the median signal of the last 100 channels (∼ 60 Gy) from all data points. The curves were then normalised to their maximum signal values. The DRC behaviour is quite similar for all three signals using SAR protocols. None of the three signals seem to provide a significant advantage in terms of onset of signal saturation and thereby an extension of the datable age range. The mean D_e values obtained with IR-RF, IRPL, and pIRIR in Sects. 4, 5, and 6 (summarised in Fig. 7) suggest an upper limit of 1000–1300 Gy for these signals. By vertically projecting the mean D_e of each signal onto the corresponding curve, we can qualitatively assess the percentage of signal saturation. Assuming the signals do not continue to grow past 4000 Gy, field saturation was achieved at ∼ 80 %–85 % saturation in all three SAR-based curves; the MAR IR-RF field saturation was slightly higher at 87 %–89 %. If the curves had been continued until full signal saturation, the percentages would be slightly lower. These results suggest a similar small long-term signal instability for the three emissions in this sample.

8 Discussion

In the present work, we re-analysed the IR-RF_RT data of 16 samples previously examined by Buylaert et al. (2012b) using an updated data analysis method for D_e estimation known as vertical slide correction. This technique accounts for sensitivity changes occurring between the natural and regenerative dose curve measurements. Application of this correction method improved the accuracy for half of the samples but led to overestimations for most of the other half (see Fig. 4a and Table 3).

We also re-measured eight of these samples with a newer and modified measurement protocol and included two additional samples of known age to expand the dataset for a following comparison with IRPL. Our new measurements differed from the original ones in three main aspects: the measurement temperature, the length of the natural dose curve measurement, and the detection window. Measuring RF at an elevated temperature to keep the shallow traps empty following the IR-RF₇₀ protocol (Frouin et al., 2017) had a large impact on D_e and hence on improving the accuracy of the resulting ages (see Fig. 4b). The temperature of 70 °C was suggested by Huot et al. (2015), corresponding to the temperature at which shallow traps are empty and also to the temperature spontaneously reached by the thermocouple during the bleaching step in their lexsyg research device. This temperature was then implemented and tested in Frouin et al. (2017) based on a series of IR-RF measurements of nine samples. As new devices have been developed, and given the temperature sensitivity of K-feldspar signals, users should conduct systematic IR-RF tests (e.g. dose recovery) to assess the protocol parameters for their samples.

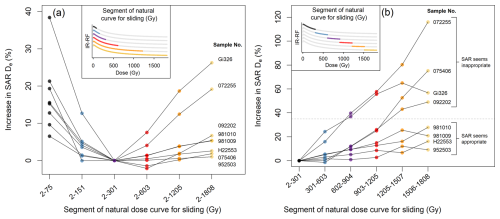
Figure 10 Test of progressive sensitivity changes during the IR-RF₇₀ natural dose curve measurement. D_e values of non-modern samples were obtained using fixed segments of the natural dose curve according to the x-axis labels with vertical and horizontal sliding (same data and colours as in (a) Fig. 5h and (b) Fig. 5j). The increase in D_e is relative to that obtained from the segment 2–301 Gy. (b) The dashed line (35 % increase) separates samples that produce D_e values within 2σ of the expected dose and those that do not.

Determining the optimal length of the natural dose curve used for sliding is challenging. In Buylaert et al. (2012b), the natural dose curve length varied between 5 and 475 Gy, depending on the sample. Contrary to our expectations, we observed continuing changes in mean D_e values when varying the natural dose curve length from ∼ 75 to ∼ 1800 Gy (Fig. 5g and h). It is important that the segment not be too short to ensure a good comparison between the natural and regenerative dose curves, especially when using the vertical slide. Here, we determined that a length of ∼ 300 Gy for the natural dose curve yielded the most promising mean D_e values in a SAR protocol, representing the intersection between two behaviours, a D_e decrease possibly caused by the segment being too short for a reliable slide and a D_e increase possibly related to sensitivity changes, as summarised in Fig. 10a. However, we stress that we do not consider this to be the definitive segment length until the mechanism behind the changes in D_e is explained. As for the vertical slide sensitivity change correction, its application led only to a small difference in the mean D_e of the four samples that agreed with the expected doses (at 2σ) and the two modern samples. In contrast, for three samples, the vertical slide led to a significant change in D_e, but neither analysis version agreed with the expected doses (Fig. 4c). Nevertheless, we recommend always using the vertical slide correction, given that sensitivity changes are known to occur and can vary in extent for different samples (e.g. compare Fig. 5g and h).

We also recommend removing initial channels to avoid the initial rise in IR-RF signal seen in most measurements. The effect of initial channel removal is dependent on the length of the natural dose curve (compare Fig. 5b, d, and f) and sample-specific characteristics. We observed no general improvement in accuracy when removing a large initial segment, e.g. ∼ 100 Gy, as suggested by the modelling in Sect. 3.2, so we recommend removing only the segments visually affected by the initial rise. Here, that corresponded to the initial ∼ 2 Gy (4 channels). Using the SAR protocol on the two modern samples, such a rejection led to slight dose underestimations (resulting in chronologically impossible negative ages), whereas no rejection yielded mean D_e values of 0.0 ± 0.6 Gy for both samples, matching the expectation (at 2σ). Similar results were found for the MAR analysis. We expect that the sharp signal peak caused by the initial rise phenomenon biases the fitting algorithm towards 0 Gy, as the peaks of the natural and regenerative dose curves align. Therefore, we suggest that the better agreement without any rejection is merely coincidental in the case of the modern samples, since the initial rise is always at the beginning of the curves, and maintain that some initial channels should be rejected. Further work would be needed on low-dose samples to explain the observed underestimation and assess the best number of rejected initial channels. However, at this stage, we caution against the reliability of IR-RF D_e values below ∼ 100 Gy, due to the possible interference from other RF emissions (see Sect. 3.2).

Returning to the non-modern samples, the only common feature among the three samples with SAR D_e values that did not match expected doses was a large increase in D_e (49 %–116 %, with a vertical slide) when using progressively higher-dose segments of the natural dose curve for sliding (Fig. 5j). The D_e increase in the four other non-modern samples was much lower (12 %–28 %), indicating lower sensitivity changes. We therefore tentatively propose using this characteristic as a screening tool to select samples that can be reliably dated by a SAR IR-RF protocol. Based on the current samples ranging ∼ 100–300 Gy, a threshold of 35 % in D_e increase in the final dose segment (∼ 1500–1800 Gy) relative to the initial dose segment (∼ 2–300 Gy) would separate the two groups (Fig. 10b). Use of a MAR protocol succeeded in obtaining D_e values compatible with the expected doses for two of the three samples with large progressive sensitivity changes (see Fig. 6a). A summary of the MAR D_e change with segment length is shown in Fig. S15.

We also compared two IR-RF₇₀ detection windows (∼ 825–860 and ∼ 875–885 nm). In theory, a detection window further into the IR would be advisable by being less prone to contamination from a red emission. However, for the present samples, no significant accuracy improvement was observed (see Fig. 4c), suggesting that the sensitivity changes occurring during the natural dose curve measurement are not caused by an overlay of an unstable emission. However, the existence of other emissions (or non-radiative recombinations) could be responsible for additional sensitivity changes by altering the proportion of electrons available for the IR-RF process, i.e. through competition effects. Such effects would be present at any detection window of the IR-RF signal. Our findings directly support the comparability of the new IR-RF results with those that would have been obtained with a Risø system, whose standard IR-RF filter has an effective detection window spanning 850–875 nm. A previous IR-RF₇₀ laboratory comparison that included both systems also supports their comparability, having yielded D_e values matching at 1σ (Murari et al., 2021).

Our comparison of IR-RF₇₀ and IRPL results indicated some interesting differences and similarities between the methods. Whatever causes the overestimation of ∼ 25–70 Gy in the IRPL signals for the two modern samples does not seem to affect the IR-RF₇₀ signal, despite our understanding that the same trap populations are being accessed. Inversely, the large overestimation of three samples with IR-RF₇₀ in the expected dose range 100–160 Gy was not observed for any of the IRPL signals, which yielded D_e values not only closer to the expected doses but, depending on the IRPL signal (see Fig. S13), even matching the expectations (at 1σ). Nevertheless, we also highlight that only one IRPL protocol was tested (i.e. a high-temperature SAR MET pIRIR-IRPL) and that other existing IRPL protocols, e.g. a low-temperature SAR MET pIRIR-IRPL (Kumar et al., 2021) or a pIR-IRPL (Duller et al., 2020), might lead to better or worse agreement with our IR-RF results.

Lastly, the DRC shape and signal saturation of the SAR IR-RF₇₀, IRPL, and pIRIR signals of sample Gi326 were very similar (see Fig. 9), with field saturation occurring below 85 % and below 90 % of the full saturation for the SAR and MAR protocols, respectively. This result aligns with the field saturation of 84 % reported by Buylaert et al. (2012b) for the IR-RF_RT signal of a different sample. Failure to reach saturation even with a pIRIR₂₉₀ signal is in agreement with the findings of Yi et al. (2016) when using a high test dose (∼ 500 Gy in their study and also here for the IRPL and pIRIR of sample Gi326). Although we report very similar IR-RF₇₀ DRC shapes for all but two samples (Fig. 8b, inset), we note that the aliquots used to obtain these curves are composed of hundreds of grains and that previous single-grain investigations have pointed to a larger DRC shape variation, including for a sample also used in the present work (Sontag-González et al., 2024). The possibility of individual grains with an earlier- or later-saturating IR-RF₇₀ DRC could explain the variability observed here for the multi-grain aliquots of some samples.

In comparison with the DRC of the SAR, the MAR IR-RF₇₀ DRC saturated slightly earlier: 85 % of the signal intensity (relative to the signal at a dose of ∼ 4000 Gy) was reached after a dose of ∼ 1050 Gy, in contrast to ∼ 1300 Gy in the DRC of the SAR. An earlier onset of saturation of the natural IR-RF₇₀ signal is also supported by a natural IR-RF₇₀ DRC built by Buchanan et al. (2022) using coarse-grain K-feldspar samples of known age from the Chinese Loess Plateau. Their natural DRC is not incompatible with the DRC of our MAR (Fig. S15a), though the high scatter in their data does not allow a definitive comparison (cf. Fig. S15b). Interestingly, and contrary to our findings, in K-feldspar MET pIRIR studies, MAR approaches have performed better for old samples due to a later onset of saturation relative to SAR and allowed D_e values of up to ca. 1100–1200 Gy (e.g. Zhang et al., 2022; Liu et al., 2025) to be determined.

9 Conclusions

We tested whether the methodological developments of the past decade have improved the accuracy of IR-RF dating of known age samples which had previously yielded inaccurate IR-RF ages with an IRSAR protocol. Specifically, we re-analysed previous data and re-measured samples using improved measurement and data analysis protocols (i.e. increased measurement temperature and vertical sliding) and new methods (i.e. MAR IR-RF and IRPL). The IR-RF age underestimation for samples in the 200–300 Gy range reported by Buylaert et al. (2012b) was likely due to the measurement temperature (room temperature) and can be overcome by raising the temperature to 70 °C (i.e. IR-RF₇₀ SAR protocol). Based on our study, we recommend the following: (i) applying the vertical slide correction to account for sensitivity changes, (ii) using a natural dose curve segment length of several hundred gray (e.g. 300 Gy) for sliding, and (iii) rejecting initial channels to mitigate the effects of the initial signal rise. Using these parameters, we observed an agreement with expected ages for four out of seven non-modern samples. However, two modern samples yielded slightly underestimated doses (ca. −2 Gy). Furthermore, we propose implementing a sensitivity change test to identify samples unsuitable for IR-RF dating through the comparison of D_e values obtained by using progressively higher-dose segments of the natural dose curve for sliding (see Fig. 10b). Although this procedure increases the measurement time, it might be a worthwhile addition until we better understand what causes the sensitivity changes during the first irradiation of some samples.

Our preliminary investigations using a MAR method suggest it holds promise, especially for samples with large sensitivity changes. However, since only six out of the nine samples of known age produced the expected D_e values, we cannot yet recommend its routine application. In our approach, application of the MAR method only required the measurement of one additional aliquot per sample after the traditional SAR measurements.

For samples ranging from ∼ 100–300 Gy, the mean D_e values derived from the pIR₅₀IRPL₉₅₅ and the APh-IRPL₈₈₀ signals are in good agreement (at 2σ) with the expected doses, including two samples strongly overestimated with IR-RF₇₀. However, IR-RF₇₀ demonstrated better agreement than any of the IRPL signals for the two modern samples.

Finally, our study points to a similar upper limit of 1000–1300 Gy for both IR-RF and IRPL, despite the regenerative DRCs of both signals not reaching complete saturation. This finding supports the notion that both techniques target the same traps and indicates that there is some instability of the stored charges.