Calibrating a long-term meteoric ¹⁰Be delivery rate into eroding western US glacial deposits by comparing meteoric and in situ produced ¹⁰Be depth profiles

Meteoric ¹⁰Be (¹⁰Be_met) concentrations in soil profiles have great potential as a geochronometer and a tracer of Earth surface processes, particularly in fine-grained soils lacking quartz that would preclude the use of in situ produced ¹⁰Be (¹⁰Be_{in situ}). One prerequisite for using this technique for accurately calculating rates and dates is constraining the delivery, or flux, of ¹⁰Be_met to a site. However, few studies to date have quantified long-term (i.e., millennial) delivery rates, and none have determined a delivery rate for an eroding soil. In this study, we compared existing concentrations of ¹⁰Be_{in situ} with new measurements of ¹⁰Be_met in eroding soils sampled from the same depth profiles to calibrate a long-term ¹⁰Be_met delivery rate. We did so on the Pinedale (∼ 21–25 kyr) and Bull Lake (∼ 140 kyr) glacial moraines at Fremont Lake, Wyoming (USA), where age, grain sizes, weathering indices, and soil properties are known, as are erosion and denudation rates calculated from ¹⁰Be_{in situ}. After ensuring sufficient beryllium retention in each profile, solving for the delivery rate of ¹⁰Be_met, and normalizing for paleomagnetic and solar intensity variations over the Holocene, we calculate ¹⁰Be_met fluxes of 1.46 (±0.20) × 10⁶ atoms cm⁻² yr⁻¹ and 1.30 (±0.48) × 10⁶ atoms cm⁻² yr⁻¹ to the Pinedale and Bull Lake moraines, respectively, and compare these values to two widely used ¹⁰Be_met delivery rate estimation methods that substantially differ for this site. Accurately estimating the ¹⁰Be_met flux using these methods requires a consideration of spatial scale and temporally varying parameters (i.e., paleomagnetic field intensity, solar modulation) to ensure the most realistic estimates of ¹⁰Be_met-derived erosion rates in future studies.

1 Introduction

¹⁰Be is a cosmogenic isotope with a half-life of 1.39 ± 0.01 Myr (Chmeleff et al., 2010), and its meteoric form (¹⁰Be_met) is produced in the atmosphere through spallation reactions as high-energy cosmic rays collide with target nuclei (i.e., ¹⁴N and ¹⁶O) in the atmosphere (Lal and Peters, 1967). ¹⁰Be_met is then delivered to the Earth's surface via precipitation or as dry deposition at a flux of 0.1–2 × 10⁶ atoms cm⁻² yr⁻¹, followed by dissolved export in runoff or, depending on retentivity, adsorption onto fine-grained reactive surfaces, typically clays and Fe and Al oxyhydroxides in soil horizons at the Earth's surface (Graly et al., 2010; Willenbring and von Blanckenburg, 2010). ¹⁰Be_met has been used as a tracer of Earth surface processes, including estimating erosion rates at the soil profile and river catchment scales, soil residence times, ages of landforms over millennial to million-year timescales, and paleo-denudation rates from marine sedimentary records (Pavich et al., 1986; McKean et al., 1993; Jungers et al., 2009; Willenbring and von Blanckenburg, 2010; von Blanckenburg et al., 2012; von Blanckenburg and Bouchez, 2014; Wittmann et al., 2015; von Blanckenburg et al., 2015; Portenga et al., 2019; Jelinski et al., 2019). Prerequisites for interpreting the concentrations and isotope ratios (i.e., ¹⁰Be_met ∕ ⁹Be) as erosion or denudation (the sum of erosion and weathering) rates, respectively, include knowing the delivery rate of ¹⁰Be_met (Pavich et al., 1986; Reusser et al., 2010; Graly et al., 2011; Heikkilä and von Blanckenburg, 2015; Dixon et al., 2018, Deng et al., 2020) and quantifying the mobility or retention of beryllium in soils (e.g., Bacon et al., 2012; Boschi and Willenbring, 2016a, b; Maher and von Blanckenburg, 2016; Dixon et al., 2018), not all of which was possible in many previous studies. The potential ability of using ¹⁰Be_met depth profiles to obtain quantitative data on soil ages, residence times, and production and denudation rates in a similar manner as in situ produced ¹⁰Be (¹⁰Be_{in situ}) depth profiles could prove to be highly advantageous, as it is easier to measure (due to much higher concentrations than ¹⁰Be_{in situ}) and can be employed in a much wider range of environments, as there is no dependence on the existence of coarse-grained quartz as is required for the analysis of ¹⁰Be_{in situ}. ¹⁰Be_{in situ} shares a cosmic ray origin with ¹⁰Be_met but differs in production method; ¹⁰Be_{in situ} is produced within crystal lattices in surface rocks and soil, rather than in the atmosphere, with a well-constrained total production rate of 4.01 atoms g⁻¹ yr⁻¹ at sea level and high latitude (Borchers et al., 2016), and it is characterized by full retentivity and known production pathways with depth. ¹⁰Be_met, in stark contrast, is potentially subjected to variable adsorption depths, incomplete retentivity, and heterogeneous internal redistribution.

In this study, we compare the previously published ¹⁰Be_{in situ} depth profiles of the Pinedale and Bull Lake terminal glacial moraines in Wind River, Wyoming (Schaller et al., 2009a, b), with new ¹⁰Be_met concentrations from depth profiles from the same sample material to evaluate the long-term (i.e., millennial) delivery rate of ¹⁰Be_met ($F_{{(}^{\mathrm{10}}{\mathrm{Be}}_{\mathrm{met}})}$) to this site. This is the first study that evaluates $F_{{(}^{\mathrm{10}}{\mathrm{Be}}_{\mathrm{met}})}$ for eroding soils as derived from the comparison of ¹⁰Be_{in situ} and ¹⁰Be_met depth profiles and erosion rates. We utilize previous knowledge of effective transient erosion rates from Schaller et al. (2009a), recalculated with revised parameters for in situ production of ¹⁰Be, to constrain and locally calibrate $F_{{(}^{\mathrm{10}}{\mathrm{Be}}_{\mathrm{met}})}$ to these moraines while considering the extent of ¹⁰Be_met retention post-delivery. We then compare the resulting calculated $F_{{(}^{\mathrm{10}}{\mathrm{Be}}_{\mathrm{met}})}$, with propagated uncertainties, with the predicted $F_{{(}^{\mathrm{10}}{\mathrm{Be}}_{\mathrm{met}})}$ of Graly et al. (2011) and Heikkilä and von Blanckenburg (2015), normalizing each result for paleomagnetic field intensity variations over the Holocene. We also explore the practical differences between these flux estimates and advocate for each approach to be carried out when estimating $F_{{(}^{\mathrm{10}}{\mathrm{Be}}_{\mathrm{met}})}$ for use in erosion rate calculations in future studies.

2 Background

2.1 Study area

The Fremont Lake area of the Wind River Mountains (Wyoming, United States) experienced multiple glacial advances during the Pleistocene, evidenced by several moraines of Pinedale and Bull Lake age (Fig. 1; modified from original mapping and descriptions by Richmond, 1973). The climate is cold, semi-arid, and windy, with a 50-year precipitation rate and temperature of 27.6 cm yr⁻¹ and 2.1 ^∘C, respectively (WRCC, 2005), in the nearby town of Pinedale, Wyoming (∼ 3.5 km southwest of the field area).

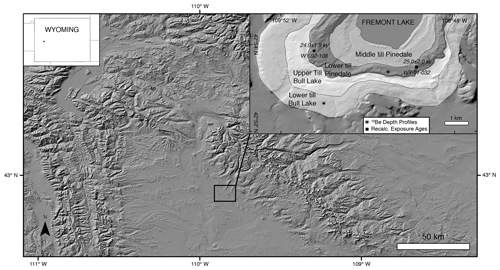
Figure 1 Hillshade map of the Wind River Range derived from a 10 m digital elevation model (DEM); the regional map encompasses the entirety of the meteoric ¹⁰Be flux map grid cell of Heikkilä and von Blanckenburg (2015). The upper left inset shows the location of the regional map within Wyoming. The upper right inset shows the locations of depth profiles analyzed for cosmogenic nuclide concentrations from the terminal Pinedale and Bull Lake moraines in the Fremont Lake area (after Richmond, 1973, and Schaller et al., 2009a). Also shown are the locations of boulder surface exposure dates for the Pinedale moraine (WY-92-108 and WY-91-032 of Gosse et al., 1995) that were recalculated using revised parameters (Table S1) to establish an updated independent age constraint for this moraine.

The Pinedale and Bull Lake aged terminal moraines (hereafter referred to as Pinedale and Bull Lake moraines) analyzed in this study (Fig. 1) were formed by highland-to-valley mountain glaciers draining an ice cap accumulation zone that covered the mountain range. The Pinedale moraine is more steep-sided and boulder-strewn than the gently sloping Bull Lake moraine, each with a total height of ∼ 30 m (see Fig. 1b, c of Schaller et al., 2009a, for detailed moraine transects). The pH of the moraine soils is well characterized; both profiles have pedogenic carbonate below 1 m, fixing the pH at depth to ∼ 8 (Chadwick and Chorover, 2001). Hall and Shroba (1995) report pH data on profiles adjacent to those analyzed in this study, with average pH ranging from ∼ 5.5 on the surface to ∼ 8 at depth.

The depth profile samples analyzed for ¹⁰Be_met reported here are the same sample material analyzed for ¹⁰Be_{in situ} by Schaller et al. (2009a). We utilize bulk samples sieved to < 2 mm for our analysis, extracted from the lower mineral soil developed on each moraine; both are mixtures of reworked glacial till (composed of Archean granite, granodiorite, and dioritic gneiss) that have a high likelihood for inheritance from cosmic ray exposure prior to burial. The same reported depths and grain size distributions apply for each sample at depth. The primary mineral content in the deepest (unweathered, > 2 mm size fraction) sample is (in order of decreasing abundance) plagioclase, quartz, biotite, K-feldspar, hornblende, and magnetite (Taylor and Blum, 1995). Secondary clay minerals in the < 2 µm size fraction include kaolinite, vermiculite, illite, and smectite (Mahaney and Halvorson, 1986), with total clay content ranging from 3 wt % to 10 wt % and 9 wt % to 30 wt % for the Pinedale and Bull Lake profiles, respectively. Major element data are reported in Schaller et al. (2009b). Sr isotope measurements of the moraine soils and dust sources showed insignificant dust fluxes in the depth profiles of the Pinedale and Bull Lake moraines (Blum and Erel, 1997; Taylor and Blum, 1997).

2.2 Independent ¹⁰Be_met flux estimation

Accurately estimating $F_{{(}^{\mathrm{10}}{\mathrm{Be}}_{\mathrm{met}})}$ from field experiments is a topic of ongoing debate (e.g., Ouimet et al., 2015; Dixon et al., 2018), particularly with regard to the effect of the precipitation rate on the flux (i.e., whether precipitation leads to additive or dilution effects on delivered ¹⁰Be_met; see Willenbring and von Blanckenburg, 2010, and Deng et al., 2020, for extensive reviews). $F_{{(}^{\mathrm{10}}{\mathrm{Be}}_{\mathrm{met}})}$ also varies through time, depending on solar modulation and paleomagnetic field intensity, and has a spatial distribution primarily resulting from atmospheric mixing and scavenging. One means to estimate ¹⁰Be_met production and delivery are $F_{{(}^{\mathrm{10}}{\mathrm{Be}}_{\mathrm{met}})}$ estimates based on global atmospheric models (Field et al., 2006; Heikkilä and von Blanckenburg, 2015), which provide an estimate over large spatial scales. Another type of estimate is based on empirical, precipitation-dependent field estimates of ¹⁰Be_met inventories in dated soils (Graly et al., 2011) measured over annual timescales. The work of Ouimet et al. (2015) highlighted the necessity of local $F_{{(}^{\mathrm{10}}{\mathrm{Be}}_{\mathrm{met}})}$ estimates that also integrate over millennial timescales against models such as these, as their comparison of ¹⁰Be_met inventories and deposition rates from Pinedale and Bull Lake aged landforms in the Colorado Front Range showed that some were lower than and some exceeded deposition rates from atmospheric models and precipitation collections.

The $F_{{(}^{\mathrm{10}}{\mathrm{Be}}_{\mathrm{met}})}$ map of Heikkilä and von Blanckenburg (2015) utilizes the ¹⁰Be_met production functions of Masarik and Beer (1999) combined with the ECHAM5 general circulation model (GCM). Production rates were scaled to reflect the solar modulation and magnetic field strength for the entire Holocene (280.94 MV) using measured ¹⁰Be concentrations in ice cores. The authors ultimately present a global grid of predicted “pre-industrial” and “industrial” (referring to simulated aerosol and greenhouse gas concentrations) Holocene $F_{{(}^{\mathrm{10}}{\mathrm{Be}}_{\mathrm{met}})}$ with an approximate cell size of 300 km × ∼ 230 km. GCMs such as this are useful for modeling atmospheric mixing of ¹⁰Be_met, particularly in the stratosphere, as well as the regional effect of climate and its influence on $F_{{(}^{\mathrm{10}}{\mathrm{Be}}_{\mathrm{met}})}$ via atmospheric circulation and precipitation (Heikkilä and Smith, 2012). At this latitude (∼ 42.9^∘ N), the pre-industrial predicted $F_{{(}^{\mathrm{10}}{\mathrm{Be}}_{\mathrm{met}})}$ of 1.38 × 10⁶ atoms cm⁻² yr⁻¹ is nearly identical to that derived from the flux map of Field et al. (2006), which utilizes the GISS (Goddard Institute for Space Studies Model E) GCM to model production. We use the pre-industrial modeled $F_{{(}^{\mathrm{10}}{\mathrm{Be}}_{\mathrm{met}})}$ in our comparisons, as it is a more appropriate estimate for landforms of these ages. To place an upper bound uncertainty on this estimate, which is otherwise hard to quantify, we utilize the difference between the industrial and pre-industrial predicted $F_{{(}^{\mathrm{10}}{\mathrm{Be}}_{\mathrm{met}})}$ (+0.99 × 10⁶ atoms cm⁻² yr⁻¹). This difference is solely a result of climate-dependent shifts in the delivery of ¹⁰Be_met and shifts resulting from large industrial aerosol loading in modern times and does not reflect changes in atmospheric production (Heikkilä and von Blanckenburg, 2015).

On the other hand, the empirical, present-day estimates of $F_{{(}^{\mathrm{10}}{\mathrm{Be}}_{\mathrm{met}})}$ from Graly et al. (2011) are based on measurements of ¹⁰Be_met deposition rates from contemporary measurements of ¹⁰Be_met in precipitation, corrected for dust and normalized to a modern (1951–2004) solar modulation value (700 MV). A first-order estimate of the $F_{{(}^{\mathrm{10}}{\mathrm{Be}}_{\mathrm{met}})}$ was empirically derived given the latitude (L) and average precipitation rate (P) of the study area (Graly et al., 2011):

$$\begin{array}{}\text{(1)}& \begin{array}{rl}{F}_{\left({}^{\mathrm{10}}{\mathrm{Be}}_{\mathrm{met}}\right)}=& P\times (\mathrm{1.44}/(\mathrm{1}+\mathrm{EXP}\left(\right(\mathrm{30.7}-L)\\ & /\mathrm{4.36}\left)\right)+\mathrm{0.63}).\end{array}\end{array}$$

Uncertainty for this type of estimate can be determined using the root mean square error (1.75 × 10³ atoms cm⁻³) of the resultant latitudinal trend in predicted $F_{{(}^{\mathrm{10}}{\mathrm{Be}}_{\mathrm{met}})}$ (see Fig. 5 of Graly et al., 2011). A predicted $F_{{(}^{\mathrm{10}}{\mathrm{Be}}_{\mathrm{met}})}$ of 0.55 (±0.05) × 10⁶ atoms cm⁻² yr⁻¹ is calculated for these Wind River moraines using Eq. (1); however, in order to compare these two estimates with each other, as well as to our calculated $F_{{(}^{\mathrm{10}}{\mathrm{Be}}_{\mathrm{met}})}$, we later normalize them all to a common paleomagnetic and solar intensity datum (i.e., the Holocene).

3 Methods

3.1 Recalculating previous age constraints

Ages for each moraine have been independently determined via multiple methods, with ¹⁰Be_{in situ} surface exposure ages of boulders combined with ²³⁰Th∕U ages of nearby contemporaneous fluvial terraces yielding the most reliable average estimates of 21 and 140 kyr for the Pinedale and Bull Lake aged moraines, respectively (Gosse et al., 1995; Phillips et al., 1997; Easterbrook et al., 2003; Sharp et al., 2003). These ages closely correspond to global maximum ice volumes of marine oxygen isotope stages 2 and 6, respectively (Sharp et al., 2003). We recalculated the ¹⁰Be boulder surface exposure ages used to constrain the timing of advancement of each moraine to its terminal position based on a recent revision of the ¹⁰Be half-life, which affected the accelerator mass spectrometry (AMS) standard values (Chmeleff et al., 2010), and the most recent nucleonic production rate of 3.92 atoms g⁻¹ yr⁻¹ at sea level and high latitude (Borchers et al., 2016) (Table S1); the updated independent age constraints are 25 kyr for the Pinedale moraine and remain at 140 kyr for the Bull Lake moraine (see the Supplement for details).

3.2 Recalculating previous denudation constraints

All moraine surfaces have been eroded to some extent after their deposition. To estimate the amount of erosion for our calculations, we utilize the previously reported denudation rates (comprising erosion and chemical loss by dissolution) for the Pinedale and Bull Lake moraines (Schaller et al., 2009a) from the same depth profiles and material analyzed in this study. The denudation rates of Schaller et al. (2009a) were calculated using a sea level, high-latitude production rate of 5.1 atoms g${}_{\text{(qtz)}}^{-\mathrm{1}}$ yr⁻¹ (Stone, 2000) and a decay constant of 4.62 × 10⁻⁷ yr⁻¹. Denudation rates were recalculated using CRONUS v.3 (Phillips et al., 2016) with the updated half-life and production rate values (Table S1 in the Supplement) and updated independent age constraints scaled to the sample altitude and latitude (Dunai, 2000) assuming two denudation rate scenarios: one of constant denudation since moraine deposition and the other of transient denudation decreasing in magnitude since moraine deposition. Recalculated average denudation rates are 32.1 ± 2.7 and 12.4 ± 4.8 mm kyr⁻¹ for the Pinedale and Bull Lake moraines, respectively, in the case of transient denudation, and they are 15 and 7.5 mm kyr⁻¹ for the Pinedale and Bull Lake moraines, respectively, in the case of constant denudation (Table 1). These recalculated denudation rates are determined from the best-fit chi square solutions obtained from running Models 2, 4, 6, and 8 of Schaller et al. (2009a) with present-day parameters (see the Supplement for details). We consider the transient denudation rates to more closely approximate reality, as moraines deposited as ∼ triangular landforms at the terminus of glaciers initially experience faster denudation than that towards present day, whereby the moraines evolve to a concave-down parabolic geometry. As the curvature of the topography is reduced over time, hillslope diffusion law dictates that the denudation rates will decrease as the moraine flattens. This approach integrates this transient behavior over the entire age of each moraines and thus likely overstates the loss of ¹⁰Be to erosion to some degree; however, it nonetheless provides the most realistic estimates possible for these moraines as we are otherwise unable to independently constrain their site-specific erosion rates.

Table 1 Recalculated chi square solutions for different denudation rate simulations of Schaller et al. (2009a)^*.

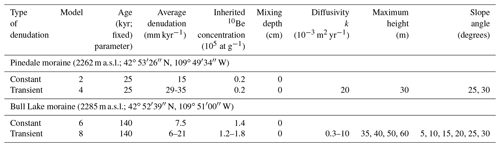
^* For a full explanation of the range allowed and resolution of each parameter, see Table 3 of Schaller et al. (2009a).

To properly compare the transient denudation rates of Schaller et al. (2009a) with the ¹⁰Be_met-derived erosion rates using the methods of von Blanckenburg et al. (2012), the weathering component of denudation must be accounted for. For the Pinedale moraine, chemical weathering mass loss is estimated to be 16 % of the denudation rate, while for the Bull Lake moraine, the chemical weathering mass loss accounts for 20 % (Schaller et al., 2009b). Assuming that the weathering mass loss took place beneath the cosmic ray attenuation pathway, the recalculated average effective transient erosion rates are then 27.0 and 9.9 mm kyr⁻¹ for the Pinedale and Bull Lake moraines, respectively. As we have no means to assess whether this assumption is correct, we instead account for this degree of potential loss in the uncertainties (in addition to analytical uncertainties) of the effective transient erosion rates in all further calculations. Regardless, we note that such weathering mass loss does not necessarily need to coincide with loss of dissolved ¹⁰Be_met. Rather, the sites of primary mineral dissolution might also be the sites of secondary mineral formation, high dissolved Ca, ensuing circumneutral pH, and hence potentially high ¹⁰Be_met retention.

3.3 ¹⁰Be_met analysis

We analyzed approximately 1–2 g aliquots of the < 2 mm grain size moraine sediment fraction from the same ∼ 10–15 cm depth intervals that Schaller et al. (2009a) analyzed for Be isotope abundance at the Laboratory for the Geochemistry of the Earth Surface at GFZ Potsdam. We followed the sediment leaching procedure described in Ebert et al. (2012) and Wittmann et al. (2012), which was adapted from Bourlès (1988) and Guelke-Stelling and von Blanckenburg (2012), to extract Be isotopes from outer grain surfaces. Bulk samples underwent two steps to remove the adsorbed beryllium: a 24 h agitation in 0.5 M HCl (to extract amorphous oxide-bound Be) and 1 M hydroxylamine–hydrochloride (to remove crystalline-bound Be). After each step, the supernate was separated from the sediment.

To measure the adsorbed ¹⁰Be_met, the two aliquots of leached material were combined and homogenized with ∼ 200 µg of ⁹Be carrier (Table 2) and 2 mL HF was added to the acid sample solution. This solution was nearly completely dried down, then dissolved in an additional 1 mL of 50 % HF acid and dried down completely, repeated once. We then added 10 mL of ultrapure (18 MΩ) water to the warm fluoride residue and leached it for 1 h on a warm hotplate. The water containing the Be was gently removed via pipette and dried down separately. The Be in the water leach solution was extracted and purified by a form of the ion exchange chromatography procedure from von Blanckenburg et al. (2004) that was adapted for ¹⁰Be_met purification by passing the leachate through anion (2 mL of BioRad 1×8 100–200 mesh resin) and cation (2×1 mL BioRad AG50-X8 200–400 mesh) exchange resins, precipitated at pH ∼ 9 using NH₄OH:H₂O (1:1), washed twice with 2 mL ultrapure water with centrifugation in between, mixed with AgCl, centrifuged and dried overnight, and finally oxidized over open flame (> 1000 ^∘C; modified from Kohl and Nishiizumi, 1992). ¹⁰Be_met ∕ ⁹Be ratios were measured at the Zurich AMS Lab (Kubik and Christl, 2010) (S555 standard, nominal ¹⁰Be∕Be = 95.5 × 10⁻¹²), from which the ¹⁰Be concentration (¹⁰Be_reac=¹⁰Be_met) was calculated. Two carrier blanks analyzed with the samples registered AMS ¹⁰Be ∕ ⁹Be ratios of 3.2 ± 1.5 × 10⁻¹⁵ and 2.2 ± 1.5 × 10⁻¹⁵ containing ≪ 0.1 % of the ¹⁰Be in analyzed samples.

Table 2 ¹⁰Be concentrations and GSD^a in depth profiles from the Pinedale and Bull Lake moraines.

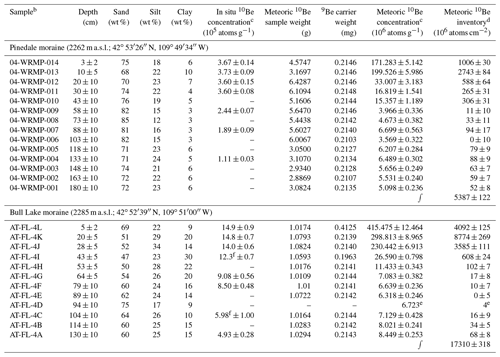
^a Grain size distributions and in situ ¹⁰Be concentrations from Schaller et al. (2009a). ^b See Schaller et al. (2009a) for the grain size fraction analyzed for each sample.^c Corrected for blank; reported error includes analytical uncertainties (1σ). ^d Corrected for inheritance. ^e Average of ¹⁰Be_met concentrations from directly above and below this depth. ^f Average of multiple aliquots analyzed in Schaller et al. (2009a).

3.4 ¹⁰Be_met flux calculations

In an actively eroding setting, erosion rates can be calculated with knowledge of (1) the total inventory of ¹⁰Be_met in the depth profile, (2) a known and/or estimated ¹⁰Be_met flux to the location, (3) the ¹⁰Be_met retention behavior, and (4) an assumption of approximate steady-state conditions, which is only justified if the inventory of ¹⁰Be_met is independent of the initial exposure age of the soil. Here, steady state means that ¹⁰Be_met lost through erosion and decay equals the ¹⁰Be_met gained from atmospheric flux (e.g., Brown et al., 1988; Willenbring and von Blanckenburg, 2010), a prerequisite of which is that the residence time of soil material containing ¹⁰Be_met with respect to erosion is much less than the depositional age (Willenbring and von Blanckenburg, 2010), which holds true for these moraines. For an assumed steady-state inventory, the inverse relationship between the local erosion rate and the ¹⁰Be_met content in the soil profile is exploited to determine a flux of ¹⁰Be_met using the formulation of Brown (1987), rearranged as follows:

$$\begin{array}{}\text{(2)}& F_{{(}^{\mathrm{10}}{\mathrm{Be}}_{\mathrm{met}})}=E\times \left({\left[{}^{\mathrm{10}}\mathrm{Be}\right]}_{\mathrm{reac}}-{\left[{}^{\mathrm{10}}\mathrm{Be}\right]}_{\mathrm{inher}}\right)+I\mathit{\lambda },\end{array}$$

where E is the erosion rate (g cm⁻² yr⁻¹), $F_{{(}^{\mathrm{10}}{\mathrm{Be}}_{\mathrm{met}})}$ is the atmospheric flux of ¹⁰Be_met (atoms cm⁻² yr⁻¹), [¹⁰Be]_inher is the inherited nuclide concentration (atoms cm⁻²), I is the inheritance-corrected inventory of ¹⁰Be_met (atoms cm⁻²) in the depth profile, λ is the decay constant of ¹⁰Be (yr⁻¹), and [¹⁰Be]_reac is the ¹⁰Be_met concentration at the surface of the soil (atoms g⁻¹). Inventories were calculated following Willenbring and von Blanckenburg (2010) using a depth-averaged regolith density (ρ) of 2.0 g cm⁻³ for each profile (Schaller et al., 2009a, b), where z is the depth to the bottom of the soil column and ([¹⁰Be]_reac (z)− [¹⁰Be]_inher) is the concentration of ¹⁰Be_met at depth minus inheritance:

$$\begin{array}{}\text{(3)}& I=\underset{\mathrm{0}}{\overset{z}{\int }}\left(\left[{}^{\mathrm{10}}\mathrm{Be}\right]\mathrm{reac}\left(\mathrm{z}\right)-\left[{}^{\mathrm{10}}\mathrm{Be}\right]\mathrm{inher}\right)\mathit{\rho }\mathrm{d}z.\end{array}$$

Both ¹⁰Be_met and ¹⁰Be_{in situ} depth profiles show indications of inherited nuclide concentrations at depth, likely due to incomplete glacial erosion resetting for each moraine (Schaller et al., 2009a) and exposure to ¹⁰Be_met during or immediately after glacial processes. Higher concentrations at depth are observed for the Bull Lake moraine for both nuclide profiles (Fig. 1, Table 2), potentially due to the presence of pre-irradiated reworked till. We consider the lowest concentration observed for each depth profile to be [¹⁰Be]_inher and subtract it from all measured concentrations.

Desorption of ¹⁰Be_met can affect the inventory of ¹⁰Be_met when erosion rates are low, water flux is high, and soil chemistry favors mobility. Given that for these soil profiles pH ranges from 8 at depth to ∼ 5.5 at the surface (Hall and Shroba, 1995), we must consider incomplete retention of beryllium and thus a reduced inventory and surface concentration used in Eq. (2) (Bacon et al., 2012; Maher and von Blanckenburg, 2016). Applying a correction directly to the calculation of ¹⁰Be_met flux is possible via a combination of (Eq. 2) (this study) and (Eq. 3) of von Blanckenburg et al. (2012), which requires an accurate estimation of the water flux out of the system (Q) and the Be partition coefficient (K_d).

$$\begin{array}{}\text{(4)}& \begin{array}{rl}{F}_{\left({}^{\mathrm{10}}{\mathrm{Be}}_{\mathrm{met}}\right)}=& E\times \left({\left[{}^{\mathrm{10}}\mathrm{Be}\right]}_{\mathrm{reac}}-\left[{}^{\mathrm{10}}\mathrm{Be}\right]\mathrm{inher}\right)+I\mathit{\lambda }\\ & +Q\times \left({\left[{}^{\mathrm{10}}\mathrm{Be}\right]}_{\mathrm{reac}}-{\left[{}^{\mathrm{10}}\mathrm{Be}\right]}_{\mathrm{inher}}\right)/K_d\end{array}\end{array}$$

K_d is estimated as 1 × 10⁵ to 1 × 10⁶ L kg⁻¹ (with an average of 5.5 × 10⁵ L kg⁻¹) from the surficial pH of ∼ 5.5 to ∼ 8 at depth via Be sorption–desorption experiments from You et al. (1989). We estimate Q by proxy via the modern precipitation rate of 276 L m⁻² yr⁻¹.

Utilizing Eq. (4) and previous knowledge of the effective transient erosion rates, we calculate the loss-corrected $F_{{(}^{\mathrm{10}}{\mathrm{Be}}_{\mathrm{met}})}$ to the locations of these moraines. To further account for the full range of possible K_d values and transient erosion rates, we use traditional algebraic error propagation to determine the uncertainty of the calculated fluxes.

3.5 Normalizing flux estimates for cosmic ray intensity variations over the Holocene

Geomagnetic field strength has varied considerably from the late Pleistocene to the present and exerts the primary quantifiable influence on temporal variability in the production rate of cosmogenic nuclides in an inverse fashion (Pigati and Lifton, 2004). Relative paleointensity over the last 140 kyr is, on average, ∼ 20 %–40 % less than the current geomagnetic intensity depending on the methodology employed (e.g., Frank et al., 1997; Valet et al., 2005). The flux map of Heikkilä and von Blanckenburg (2015) accounts for paleomagnetic field and solar intensity variations over the Holocene via the reconstruction method of Steinhilber et al. (2012), which effectively increases the production rate used in their model by 1.23 times the present-day rate by rescaling the modern solar modulation factor (500 MV) and associated geomagnetic field intensity to that of the Holocene average (280.94 MV). As the estimations of flux from Graly et al. (2011) were normalized to reflect a solar modulation of 700 MV, we rescaled the modern Graly-derived $F_{{(}^{\mathrm{10}}{\mathrm{Be}}_{\mathrm{met}})}$ to the average Holocene solar modulation factor of 280.94 MV used in the flux map of Heikkilä and von Blanckenburg (2015) following the paleomagnetic and solar intensity normalization procedure of Deng et al. (2020). This is carried out by first rescaling production at 700 to 500 MV (i.e., the modern solar modulation factor of Steinhilber et al., 2012) via Fig. 4B of Masarik and Beer (2009) for a Graly et al. (2011) modern production ratio of 0.82 (Table 3). Then, to properly normalize for the Holocene, we multiply this modern production ratio by the reciprocal of the rescaling production ratio of Heikkilä and von Blanckenburg (2015) (1.23) to arrive at a Holocene-normalized production ratio of 0.67 and apply this to the Graly et al. (2011) flux estimate (Table 3). We illustrate and further describe the details of this procedure in the Supplement (Fig. S1).

Table 3 ¹⁰Be_met flux estimates, raw and normalized for Holocene paleointensity variations.

^a Using the measured ¹⁰Be_met seafloor accumulation record of Christl et al. (2010) from 6 and 24 kyr to the present for the Pinedale and Bull Lake moraines, respectively. ^b Using the paleomagnetic scaling method of Masarik and Beer (2009). ^c Using the paleomagnetic reconstruction method of Steinhilber et al. (2012). ^d Uncertainty represents the difference between the “industrial” and the “pre-industrial” modeled flux of Heikkilä and von Blanckenburg (2015).

To further compare the model- and precipitation-derived Holocene average $F_{{(}^{\mathrm{10}}{\mathrm{Be}}_{\mathrm{met}})}$ estimates with those calculated in this study, we must also normalize for geomagnetic and solar intensity variations within the Holocene (for Pinedale with a 6 kyr cosmogenic integration time) and beyond the Holocene (for Bull Lake with a 24 kyr cosmogenic integration time). We again linearly rescaled our calculated loss-corrected $F_{{(}^{\mathrm{10}}{\mathrm{Be}}_{\mathrm{met}})}$ for the Pinedale and Bull Lake moraines by first integrating the production rate relative to the modern using principal component 1 (PC1) of the ¹⁰Be marine core record of Christl et al. (2010), converting PC1 into relative fluxes from 6 and 24 kyr, respectively, and then normalizing these values to those over the Holocene, propagating the statistical uncertainties. These time intervals represent the calculated residence and integration times of the soil profiles from the surface to the e-folding adsorption depth of ¹⁰Be_met (20 and 30 cm for the Pinedale and Bull Lake moraines, respectively). This approach accounts for the cumulative effects of transient erosion and leaching by weighting geomagnetic intensity variations of $F_{{(}^{\mathrm{10}}{\mathrm{Be}}_{\mathrm{met}})}$ towards the present.

4 Results

4.1 Meteoric cosmogenic ¹⁰Be concentrations

The measured ¹⁰Be_met concentrations are reported along with the previously published ¹⁰Be_{in situ} concentrations (Schaller et al., 2009a) for the Pinedale and Bull Lake profiles (Table 2); ¹⁰Be_met depth profiles are presented for the Pinedale and Bull Lake profiles in Fig. 2. The Pinedale depth profile has ¹⁰Be_met concentrations ranging from 3.57 (±0.32) to 199.53 (±5.26) × 10⁶ atoms g⁻¹. The highest nuclide concentration is measured at 10 cm rather than at the surface. Below this maximum value, concentrations decrease exponentially until reaching an asymptote at ∼ 3 to 6 × 10⁶ atoms g⁻¹ from 43 cm to the bottom of the profile (180 cm), the lowest of which we consider to be an inherited component. The Pinedale depth profile has a calculated, inheritance-corrected inventory (Eq. 3) of 5387 (±122) × 10⁶ atoms cm⁻².

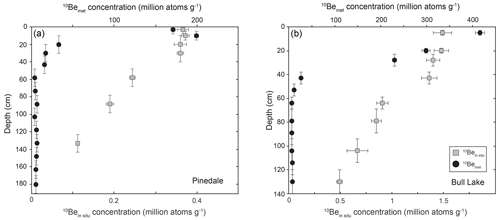
Figure 2 (a) Depth profile for the Pinedale moraine; ¹⁰Be_met concentrations were measured from the < 2 mm grain size fraction of 14 samples from the same depth profile as analyzed for ¹⁰Be_{in situ} in Schaller et al. (2009a). (b) Depth profile for the Bull Lake moraine; ¹⁰Be_met concentrations were also measured from the < 2 mm grain size fraction of 11 samples from the same depth profile as analyzed for ¹⁰Be_{in situ} in Schaller et al. (2009a). The ¹⁰Be_met concentration at 94 cm was not measured.

The Bull Lake depth profile has ¹⁰Be_met concentrations ranging from 6.32 (±0.25) to 415.48 (±12.46) × 10⁶ atoms g⁻¹. The highest nuclide concentration is measured at the surface; below this, concentrations decrease in an approximately exponential fashion until reaching an asymptote at ∼ 6 to 8 × 10⁶ atoms g⁻¹ from 64 cm to the bottom of the profile (130 cm), the lowest of which we also consider to be an inherited component. The Bull Lake depth profile has a calculated, inheritance-corrected inventory (Eq. 3) of 17 310 (±318) × 10⁶ atoms cm⁻². The ¹⁰Be_met inventory from the Bull Lake moraine is roughly 3 times higher than that of the Pinedale moraine.

4.2 ¹⁰Be_met fluxes

The loss-corrected $F_{{(}^{\mathrm{10}}{\mathrm{Be}}_{\mathrm{met}})}$ as calculated from Eq. (4) is 1.04 (±0.14) × 10⁶ atoms cm⁻² yr⁻¹ and 1.04 (±0.39) × 10⁶ atoms cm⁻² yr⁻¹ for the Pinedale and Bull Lake moraines, respectively (Table 3), with uncertainties determined via traditional algebraic error propagation, assuming a Gaussian distribution for the estimated K_d and transient erosion rate values.

Retention calculations from (Eq. 4) across the entire range of possible K_d values indicate that the potential desorption loss at the surface of the Pinedale and Bull Lake profiles ranges from 0.4 % to 3.6 % and 0.9 % to 8.9 %, respectively. The average calculated loss (reported above) compared to calculations without considering retention is 0.8 % and 2.0 % for the Pinedale and Bull Lake profiles, respectively.

These loss-corrected calculated fluxes are then normalized for paleomagnetic field intensity variations over the Holocene and compared in order to evaluate the $F_{{(}^{\mathrm{10}}{\mathrm{Be}}_{\mathrm{met}})}$ to this area. The Holocene average loss-corrected $F_{{(}^{\mathrm{10}}{\mathrm{Be}}_{\mathrm{met}})}$ values from this study are 1.46 (±0.20) × 10⁶ atoms cm⁻² yr⁻¹ and 1.30 (±0.48) × 10⁶ atoms cm⁻² yr⁻¹ for the Pinedale and Bull Lake moraines, respectively (Table 3).

The predicted Holocene average $F_{{(}^{\mathrm{10}}{\mathrm{Be}}_{\mathrm{met}})}$ of Graly et al. (2011) for this site is 0.83 (±0.08) × 10⁶ atoms cm⁻² yr⁻¹ (Table 3). As the pre-industrial flux map of Heikkilä and von Blanckenburg (2015) already presents a Holocene average $F_{{(}^{\mathrm{10}}{\mathrm{Be}}_{\mathrm{met}})}$ of 1.38 (+0.99) × 10⁶ atoms cm⁻² yr⁻¹, no normalization for this method needs to be carried out.

5 Discussion

5.1 Cosmogenic nuclide profiles

An approximately exponential decrease in ¹⁰Be_met with depth is observed for the Pinedale and Bull Lake moraines (Fig. 2). This trend can be explained most simply by the reactive transport of dissolved ¹⁰Be_met with infiltrating water (e.g., Willenbring and von Blanckenburg, 2010), as exponential ¹⁰Be_met profiles are predicted by reactive transport models (Maher and von Blanckenburg, 2016).

The maximum ¹⁰Be_met concentration for the Pinedale moraine is measured at 10 cm of depth rather than the most surficial sample (3 cm). This peak concentration corresponds to the clay-rich layer of the B horizon in the soil profile (Table 2). This potentially indicates that this layer acts as a zone of illuviation, often observed in soil profiles that contain a mid-depth clay-rich horizon (e.g., Monaghan et al., 1992) formed by vertical transport of soil particles containing ¹⁰Be_met (Jagercikova et al., 2016). This subsurface maximum could be the result of smaller grain sizes within this horizon, as these grains have a higher surface area per unit mass and can exchange ions more easily (Brown et al., 1992; Willenbring and von Blanckenburg, 2010). Alternatively, enhanced ¹⁰Be_met incorporation into the lattices of newly formed clays and oxyhydroxides at depth (e.g., Barg et al., 1997) might explain this maximum. This phenomenon is not observed for the Bull Lake moraine; the highest clay content observed in the profile is in the Bk horizon at a depth of 43 cm (Schaller et al., 2009a, b); however, no increase or anomalously high ¹⁰Be_met concentration is observed (Fig. 2, Table 2). It is possible that such an increase may have been missed in the Bull Lake profile, as the equivalent 10 cm depth interval was not sampled.

Peculiarly, the observed mixing depths for the Pinedale and Bull Lake moraines as determined from the ¹⁰Be_{in situ} depth profiles of Schaller et al. (2009a) (∼ 40 and 50 cm, respectively) are not observed for the ¹⁰Be_met depth profiles (Fig. 2). A couple of viable reasons for the lack of a mixing signal in the ¹⁰Be_met depth profiles exist. The different grain sizes analyzed here and in Schaller et al. (2009a) might exhibit different diffusion coefficients, by which larger grain sizes are more easily mixed; however, a trend in smaller grain size fractions with depth within the ¹⁰Be_{in situ} mixing layer would likely be observed if this were the case. Unfortunately, separate grain size classes were not measured for ¹⁰Be_{in situ} within the full mixing zone of either profile to further assess this explanation. Another possibility is that the advection of ¹⁰Be_met from the surface swamps the effect of mixing that is apparent in the ¹⁰Be_{in situ} depth profiles. This could indicate that continual ¹⁰Be_met delivery and reactive flow reset the ¹⁰Be_met profile at timescales much shorter than that of physical mixing. Profiles with a relatively low surficial pH (< 5) might be particularly susceptible to this phenomenon due to incomplete retention or differential mobility of ¹⁰Be_met (Kaste and Baskaran, 2012), although the profiles analyzed here are not likely to show appreciable (> 9 %) ¹⁰Be_met loss at depth due to retention issues. Nonetheless, the formation of a clay horizon in the Pinedale moraine may indicate that soil horizonation happens more rapidly than soil mixing, as inferred from the ¹⁰Be_{in situ} depth profile (Schaller et al., 2009a), suggesting that ¹⁰Be_met advection from the surface is a more likely explanation.

5.1.1 ¹⁰Be_met retention

A range of possibilities exist for retention effects and associated surficial ¹⁰Be_met loss for these profiles. For the highest K_d estimate, at 1 × 10⁶ L kg⁻¹, potential loss is as low as 0.4 % and 0.8 % for the Pinedale and Bull Lake profiles, respectively. For an average K_d of 5.5 × 10⁵ L kg⁻¹, the potential loss is likewise negligible, at 0.8 % and 2.0 % for the Pinedale and Bull Lake profiles, respectively. On the other hand, for the lowest K_d estimate, at 1 × 10⁵ L kg⁻¹, ¹⁰Be_met loss due to desorption could be as great as 3.6 % and 8.9 % at the surface of the Pinedale and Bull Lake profiles, respectively. While the possibility of desorption cannot be ruled out, it is unlikely that either profile has experienced loss to such a degree, as pH, and thus K_d and retentivity, increases with depth. Even in the worst-case scenario of assuming maximum possible loss at the lowest K_d estimate, the magnitude of the potential loss does not substantially affect our calculated $F_{{(}^{\mathrm{10}}{\mathrm{Be}}_{\mathrm{met}})}$ estimates within uncertainties. Our calculations thus capture the potential maximum bound for loss via propagated uncertainties.

5.2 ¹⁰Be_met flux estimation; sources of variability

The calculated as well as loss- and paleointensity-corrected $F_{{(}^{\mathrm{10}}{\mathrm{Be}}_{\mathrm{met}})}$ of 1.46 (±0.20) × 10⁶ atoms cm⁻² yr⁻¹ and 1.30 (±0.48) × 10⁶ atoms cm⁻² yr⁻¹ for the Pinedale and Bull Lake moraines, respectively, are higher compared to that estimated by Graly et al. (2011), at 0.83 × 10⁶ atoms cm⁻² yr⁻¹, and agree within uncertainty with that predicted by Heikkilä and von Blanckenburg (2015), at 1.38 × 10⁶ atoms cm⁻² yr⁻¹ (Table 3). The considerable discrepancy between the predicted $F_{{(}^{\mathrm{10}}{\mathrm{Be}}_{\mathrm{met}})}$ of each method arises primarily from differences in how each methodology treats the influence that the precipitation rate has on the flux to a given area and, in particular for this study, how large of an area is covered. The 310 km × 228 km flux map grid cell of Heikkilä and von Blanckenburg (2015) covers the entirety of the Wind River Range and the surrounding relatively low-lying flatlands (Fig. 1), where precipitation estimates vary considerably by over an order of magnitude (WRCC, 2005) due to elevation and topographic effects on precipitation (Hostetler and Clark, 1997). For example, if one were to estimate $F_{{(}^{\mathrm{10}}{\mathrm{Be}}_{\mathrm{met}})}$ from Graly et al. (2011) via Eq. (1) to nearby Fish Lake Mountain contained within the same Heikkilä and von Blanckenburg (2015) grid cell as this study site with a modern precipitation rate of 128 cm yr⁻¹ (WRCC, 2005), the $F_{{(}^{\mathrm{10}}{\mathrm{Be}}_{\mathrm{met}})}$ would be 2.5 × 10⁶ atoms cm⁻² yr⁻¹, substantially higher than that predicted from Heikkilä and von Blanckenburg (2015). Considering this alone, it is not surprising that such a discrepancy exists between methods, nor is this a unique occurrence (e.g., Jungers et al., 2009; Schoonejans et al., 2017; Dixon et al., 2018; Deng et al., 2020).

Each approach has its own set of shortcomings, precluding agreement between each approach at sites such as this. The flux map of Heikkilä and von Blanckenburg (2015) has a coarse resolution and does not handle short-wavelength orographic effects well, along with being model-based and requiring many assumptions on atmospheric scavenging. The formula of Graly et al. (2011), on the other hand, does not take atmospheric circulation into account, instead relying on data from sites with relatively high rates of precipitation to derive an empirical formula. Recent work by Deng et al. (2020) highlights the potential for precipitation estimates to differ from GCM-derived estimates due to short-timescale additive effects (sensu Willenbring and von Blanckenburg, 2010). Further, they find that in the majority of studies globally, GCM- and soil-derived $F_{{(}^{\mathrm{10}}{\mathrm{Be}}_{\mathrm{met}})}$ estimates agree within a factor of 2. That the calculated fluxes of this study agree with the GCM-modeled pre-industrial $F_{{(}^{\mathrm{10}}{\mathrm{Be}}_{\mathrm{met}})}$ of Heikkilä and von Blanckenburg (2015) provides further evidence of this general observation. In any event, the strength of future ¹⁰Be_met studies relies upon careful consideration of beryllium retention, spatial scale, and paleomagnetic intensity when determining $F_{{(}^{\mathrm{10}}{\mathrm{Be}}_{\mathrm{met}})}$. As calculating a long-term delivery rate of $F_{{(}^{\mathrm{10}}{\mathrm{Be}}_{\mathrm{met}})}$ for a particular site using ¹⁰Be_{in situ} and ¹⁰Be_met is both costly and time-intensive, it is especially prudent to estimate $F_{{(}^{\mathrm{10}}{\mathrm{Be}}_{\mathrm{met}})}$ using both methods compared here for robust calculations utilizing $F_{{(}^{\mathrm{10}}{\mathrm{Be}}_{\mathrm{met}})}$ (e.g., ¹⁰Be_met-derived erosion rates) in the future.

6 Conclusions

In this study, we compare new meteoric ¹⁰Be (¹⁰Be_met) and previously published in situ produced ¹⁰Be (¹⁰Be_{in situ}) depth profile measurements from the well-characterized Pinedale (∼ 21–25 kyr) and Bull Lake (∼ 140 kyr) moraines of Wind River, Wyoming. Our ability to utilize previous knowledge of transient erosion rates from the ¹⁰Be_{in situ} depth profile measurements of Schaller et al. (2009a), recalculated with revised parameters, allows us to calculate loss-corrected Holocene average ¹⁰Be_met fluxes of 1.46 (±0.20) × 10⁶ atoms cm⁻² yr⁻¹ and 1.30 (±0.48) × 10⁶ atoms cm⁻² yr⁻¹ to the Pinedale and Bull Lake moraines, respectively. Comparing these fluxes to two independent estimation methods reveals that the empirical flux estimate of Graly et al. (2011) of 0.83 (±0.08) × 10⁶ atoms cm⁻² yr⁻¹, after normalizing for Holocene paleomagnetic intensity, is lower than the calculated fluxes, and the modeled Holocene flux estimate of Heikkilä and von Blanckenburg (2015), at 1.38 × 10⁶ atoms cm⁻² yr⁻¹, agrees within uncertainty with the calculated fluxes. We find that loss of ¹⁰Be_met in these profiles due to pH-influenced mobility and dissolution effects exerts a relatively minor potential control (biasing from < 1 % up to 9 % in the most extreme case) on flux calculations. Inspection of the ¹⁰Be_met depth profiles and their near-surface concentrations suggests that soil mixing to depths of 40 and 50 cm, as observed for the Pinedale and Bull Lake ¹⁰Be_{in situ} depth profiles, respectively, is not represented by the finer grain sizes analyzed in this study. The lack of a mixing signal may be most simply explained by a swamping effect from continual delivery and advection of ¹⁰Be_met from the surface that occur over more rapid timescales than soil mixing. These differences in the depth–concentration relationships between ¹⁰Be_met and ¹⁰Be_{in situ} might open up a new area of research to study particle movement in soils.