the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
On the treatment of discordant detrital zircon U–Pb data
Zircon U–Pb geochronology is a staple of crustal evolution studies and sedimentary provenance analysis. Constructing (detrital) U–Pb age spectra is straightforward for concordant and compositions. But unfortunately, many U–Pb datasets contain a significant proportion of discordant analyses. This paper investigates two decisions that must be made when analysing such discordant U–Pb data.
First, the analyst must choose whether to use the or the date. The method is more precise for young samples, whereas the method is better suited for old samples. However there is no agreement which “cutoff” should be used to switch between the two. This subjective decision can be avoided by using single-grain concordia ages. These represent a kind of weighted mean between the and methods, which offers better precision than either of the latter two methods.
A second subjective decision is how to define the discordance cutoff between “good” and “bad” data. Discordance is usually defined as (1) the relative age difference between the and dates. However, this paper shows that several other definitions are possible as well, including (2) the absolute age difference; (3) the common-Pb fraction according to the Stacey–Kramers mantle evolution model; (4) the p value of concordance; (5) the perpendicular log ratio (or “Aitchison”) distance to the concordia line; and (6) the log ratio distance to the maximum likelihood composition on the concordia line.
Applying these six discordance filters to a 70 869-grain dataset of zircon U–Pb compositions reveals that (i) the relative age discordance filter tends to suppress the young age components in U–Pb age spectra, whilst inflating the older age components; (ii) the Stacey–Kramers discordance filter is more likely to reject old grains and less likely to reject young ones; (iii) the p-value-based discordance filter has the undesirable effect of biasing the results towards the least precise measurements; (iv) the log-ratio-based discordance filters are strictest for Proterozoic grains and more lenient for Phanerozoic and Archaean age components; (v) of all the methods, the log ratio distance to the concordia composition produces the best results, in the sense that it produces age spectra that most closely match those of the unfiltered data: it sharpens age spectra but does not change their shape. The popular relative age definition fares the worst according to this criterion. All the methods presented in this paper have been implemented in the IsoplotR toolbox for geochronology.
Please read the corrigendum first before continuing.
-
Notice on corrigendum
The requested paper has a corresponding corrigendum published. Please read the corrigendum first before downloading the article.
-
Article
(2418 KB)
-
The requested paper has a corresponding corrigendum published. Please read the corrigendum first before downloading the article.
- Article
(2418 KB) - Full-text XML
- Corrigendum
- BibTeX
- EndNote
The U–Pb method consists of two paired-decay systems, in which two isotopes of the same radioactive parent (238U and 235U) decay to two isotopes of the same radiogenic daughter (206Pb and 207Pb, respectively). This paired-decay system provides a powerful internal consistency check for the method, which is absent from other chronometers. By “double dating” samples with the and methods (or, equivalently, the and methods) it is possible to verify whether the isotopic system is free of primary or secondary disturbances. The most reliable age constraints are obtained from samples whose , , and ages are statistically indistinguishable from each other. U–Pb compositions that fulfil this requirement are “concordant”. Those that fail to meet it are “discordant”.
Discordance can be caused by a number of mechanisms, including (a) the presence of non-radiogenic (“common”) lead; (b) initial disequilibrium between the short-lived nuclides of the 238U−206Pb and 235U−207Pb decay chains; (c) partial loss of radiogenic lead during high grade metamorphism; and (d) mixing of different age domains during micro-analysis (Schoene, 2014). These complicating effects can often be diagnosed and remediated when multiple cogenetic crystals are available from the same sample. If the aliquots form an isochron (or “discordia”) line in U–Pb isotope space, then this line can be used to recover robust chronologies from discordant data (Ludwig, 1998).
Unfortunately, this procedure is rarely or never possible for detrital samples, in which crystals of datable minerals are not guaranteed to be cogenetic. Without a universal mechanism to identify the cause of U–Pb discordance and remove its effects, detrital geochronologists have no choice but to accept some discordant analyses and somehow incorporate them into their age spectra. There exists a lack of consensus among the detrital zircon geochronology community on how to do this. Two outstanding questions are as follows:
-
Which age estimate should be used? It is widely recognized that age estimates offer the optimal accuracy and precision at the young end of the age spectrum, whereas the method is better suited for older samples. However the cutoff between the two clocks varies between studies, with values ranging from 800 Ma to 1.5 Ga (Gehrels, 2011; Spencer et al., 2016).
-
How should discordance be quantified? Most studies define discordance as the relative age difference between the and ages, but some advocate the use of statistical hypothesis tests and p values to quantify discordance (Spencer et al., 2016). And even when a discordance definition has been agreed upon, there are many ways to choose the discordance cutoff. For example, the relative age discordance threshold may vary between 10 % and 30 % (Gehrels, 2011).
This paper addresses both of these issues. Section 2 advocates the use of single-grain concordia ages (Ludwig, 1998) as a way to avoid the arbitrary cutoff between the and methods. Although previous workers have argued for the use of single-grain concordia ages before (see Zimmermann et al., 2018, for a recent example), this study uses a semi-analytical model, rather than purely empirical arguments, to demonstrate the superior precision of this hybrid chronometer.
Section 3 compares and contrasts existing discordance filters based on age disparity and p values. It shows that the relative age definition strongly favours older samples over young ones and that the p value definition, which has gained popularity in recent years, hurts both the accuracy and precision of detrital geochronology. The age disparity and p value definitions are heuristic by nature and are not based on firm statistical or geological arguments. Although they are the two most popular definitions of discordance in use today, they are by no means the only two possible options.
Section 4 addresses the inherent biases of the existing discordance definitions by proposing three new definitions, which are based directly on U–Pb compositions rather than on the ages calculated therefrom. The first new definition assumes that the discordance is caused by the presence of common lead. The other two new definitions treat U–Pb discordance as a compositional data problem (sensu Aitchison, 1986). Isotope ratios are strictly positive quantities and log contrasts are the “natural” way to quantify “distances” between them. Section 4 introduces two log ratio definitions of discordance, ignoring and accounting for analytical uncertainty, respectively.
Although the new definitions are arguably more attractive than the old ones from a theoretical point of view, this does not guarantee that they produce more sensible results. To test their performance on real data, Sect. 5 applies the discordance filters to a compilation of zircon U–Pb data. Although the true age distribution of this dataset is unknowable, the results suggest that the log-ratio-based discordance filters produce the most accurate and most easily interpretable results. The relative age definition fares the worst.
The U–Pb method is based on three separate chronometers: , , and . The half-life of 235U is more than 6 times shorter than that of 238U, and 235U is more than 100 times less abundant than 238U. For these two reasons, little 207Pb has been produced during the last billion years of Earth history compared to 206Pb. Consequently, the and methods are less precise than the method during the Phanerozoic and Neoproterozoic.
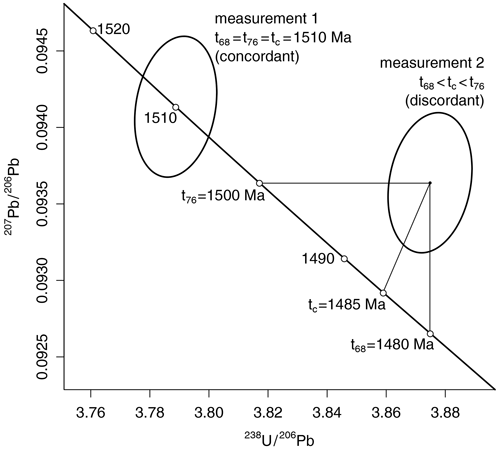
Figure 1Illustrative Tera–Wasserburg concordia diagram with a concordant and discordant measurement. t68 marks the age, t76 the age, and tc the concordia age. Measurement 1 is concordant because its estimates for t68, t76, and tc are identical. Measurement 2 is discordant because the three estimates disagree. The concordia age is the most likely age given the analytical uncertainties. It falls between the other two age estimates and offers the best analytical precision of the three.
However, during earlier stages of Earth's history, 235U was significantly more abundant than it is today. The ratio was ∼60 at 1 Ga, ∼26 at 2 Ga, ∼11 at 3 Ga, and ∼5 at 4 Ga. Due to the greater abundance of 235U in this past and because it decays much faster than 238U, the precision of the and clocks exceeds that of the method during the Palaeoproterozoic and Archaean. The gradual shift in sensitivity between the two chronometers is visible in the slope of a Tera–Wasserburg concordia line, which is steep at old ages (high gradient with respect to time) and shallow at young ages (low gradient with respect to time).
Most published detrital zircon U–Pb studies switch from to at some point during the Proterozoic. Unfortunately there are two problems with such a switch. First, it requires the selection of a discrete discordance cutoff between the two methods. If this cutoff differs between two studies (which it often does), then this complicates the intercomparison of their respective age spectra. Second, the sudden switch between the and clocks is often marked by a discrete step in the age spectrum (Puetz et al., 2018). This step is entirely artificial and obscures any geologically significant events that might occur around the same time.
Both of these problems can be solved by using “hybrid” concordia ages instead of “pure” and ages. Concordia ages are defined by Ludwig (1998) as the “most likely” (in a statistical sense) U–Pb age given the isotopic ratio composition and its analytical uncertainty (Fig. 1). Let r86 and r76 be the measured and ratios, respectively; let σ[r86]2, σ[r76]2, and σ[r86,r76] be their (co)variances; and let , , and . Then the concordia age tc is obtained by numerically minimizing the sum of squares S1:
The single-grain concordia age combines the chronometric power of the and systems. For young (<1 Ga) samples, the concordia age is nearly identical to the age. For old samples (>2 Ga) it approaches the age. Using concordia ages removes the need for an arbitrary cutoff between the two chronometers. An additional advantage is that the concordia age offers better precision than the and the chronometer (or the matter for that matter). Figure 2 quantifies this effect using a semi-analytical mass spectrometry simulation whose algorithm is provided in Appendix A.
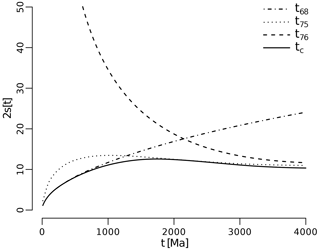
Figure 2Predicted uncertainties of the (t68), (t75), (t76), and concordia (tc) ages for a synthetic dataset with a constant uranium concentration. Dwell times and detector sensitivities were chosen so as to yield results that are similar to those obtained from real data. The concordia age (solid line) always offers the best precision. See Appendix A for further details about the calculations behind this figure.
The most common definition of discordance uses the relative difference between the and age estimate (Gehrels, 2011):
However other definitions are possible as well. For example, one could also define discordance in terms of absolute age differences (Puetz et al., 2018):
A third option is to define discordance in terms of U–Pb compositions rather than ages. Spencer et al. (2016) advocate using p values to assess concordance. In the context of single-grain concordia ages, the p value is the probability that the sum of squares S (Eq. 1) exceeds the observed value under a chi-square distribution with 2 degrees of freedom:
Zircon U–Pb data can be filtered by removing all measurements whose discordance values exceed a certain threshold value. Typical cutoff values for dr are 10 %–30 % (Gehrels, 2011), whereas dp is generally set to 5 % (Spencer et al., 2016). Different discordance criteria produce different U–Pb age spectra. For example, a relative age cutoff will preferentially remove young grains, whereas an absolute age cutoff is comparatively more likely to remove old grains (Fig. 3).
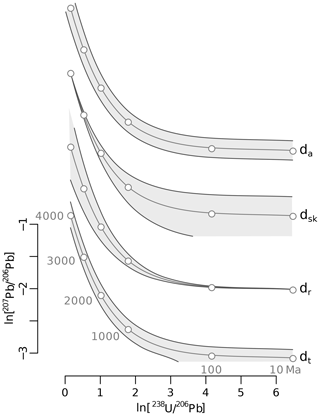
Figure 3Discordance cutoffs for four of the six discordance definitions discussed in Sects. 3 and 4. The dp and dc criteria are not shown because they depend on the analytical uncertainty of the measurements, which may vary between studies. The grey envelopes mark cutoff values of dr=20 % (relative age filter), dt=300 Myr (absolute age filter), dsk=2 % (Stacey–Kramers filter), and da=15 % (perpendicular Aitchison distance) on a Tera–Wasserburg concordia diagram, which is plotted in logarithmic space to provide a more balanced view of the old and young ends of the timescale. The dsk and dt envelopes are truncated where they cross over into physically impossible negative isotope ratio space.
The p value definition affects grains differently depending on their analytical precision (Nemchin and Cawood, 2005). For example, consider a 1.5 Ga zircon that is dr=1 % discordant. If this grain were analysed by laser ablation inductively coupled plasma mass spectrometry (LA-ICP-MS) with an analytical precision of 2 %, say, then it would pass the chi-square test and be accepted as being concordant. However, if that same grain were analysed by thermal ionization mass spectrometry (TIMS) with a precision of 0.2 %, then the p value criterion would reject it as being discordant. It seems fundamentally wrong that an imprecise analytical method would be favoured over a precise one (Fig. 4). This is a pertinent problem because technical innovations are increasing the precision of all analytical approaches to U–Pb geochronology. As precision improves, so does the ability to detect ever small degrees of discordance. Using the p value criterion, there may come a time when no zircon passes this filter.
A final argument against the p value discordance criterion is that it biases against old U–Pb ages. This is because old zircon contains more radiogenic Pb than young zircon does. Therefore the analytical precision of the isotopic ratio measurements tends to be better for old grains than it is for young ones. Consequently, the chi-square test has greater power (sensu Cohen, 1992) to reject them. In conclusion, p-value-based discordance filters are fundamentally flawed. Despite their appeal as “objective” tools for statistical decision making, formalized hypothesis tests such as chi-square are rarely useful in geology. For the same reason, the widely used MSWD (mean square of the weighted deviates; McIntyre et al., 1966) statistic (which is just in this case) should be used with caution. This is because, like p values, MSWD cutoffs also punish precise datasets in favour of imprecise ones. Note that this caveat also goes against the recommendations of Spencer et al. (2016).
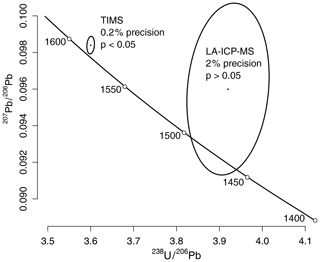
Figure 4Application of the flawed p value discordance criterion to two synthetic measurements by TIMS (left) and LA-ICP-MS (right). The precise TIMS measurement is labelled as discordant even though it plots closer to the concordia line than the imprecise LA-ICP-MS measurement, which is labelled as concordant.
Section 3 reviewed three existing discordance definitions. This section will introduce three new ones. None of the definitions discussed thus far encode any information about the geological mechanisms behind the discordance. As explained in Sect. 1, common Pb is one of the most likely causes of discordance. Using a mantle evolution model (e.g. Stacey and Kramers, 1975) to approximate the isotopic composition of this common Pb, discordance can be defined as
where is the ratio of the intersection between concordia and a straight line connecting the measurement to the inferred mantle composition (Fig. 5).
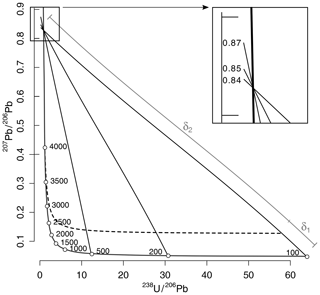
Figure 5Using the Stacey and Kramers (1975) common-Pb model as a discordance criterion. This criterion assumes that the discordance is caused by linear mixing (hence, the linear scale of this Tera–Wasserburg plot) between radiogenic Pb (intersections of the mixing lines with concordia) and common Pb (intersection of the mixing lines with the vertical axis; see inset). The dashed line marks the 20 % () discordance cutoff. This discordance filter, which must be applied before making any actual common-Pb correction, is more forgiving for young grains than it is for old grains. In this respect, it has the opposite effect of the relative age filter shown in Fig. 3.
The common-Pb definition of discordance is more forgiving for young grains than it is for old ones. Importantly, if the discordance is caused by common Pb, then the , , and concordia age estimates are all positively biased with respect to the true age. However this bias can be removed by applying a common-Pb correction after the data have been filtered.
Even though Eq. (5) is mathematically able to produce negative discordance values, such values lack a geologically meaningful interpretation because it is impossible for minerals to inherit negative amounts of common Pb. Thus it is sensible to set a minimum cutoff of dsk>0 when using the Stacey–Kramers filter.
Each discordia definition that we have studied thus far is expressed in different units. For the absolute age definition, degrees of discordance are expressed in units of time (ranging from 0 to 4.5 Ga). The relative age definition uses fractions of time (ranging from −∞ to 1). The p value definition expresses discordance in terms of probability (ranging from 0 to 1). And the Stacey and Kramers (1975) definition uses fractions of ratios (ranging from −∞ to 1). None of these scales is particularly intuitive or natural. They certainly do not match the usual definition of distance in the geographical sense of the word.
To address this issue, it is useful to subject the U–Pb isotopic ratio data to a logarithmic transformation. So instead of analysing the data on a conventional Tera–Wasserburg concordia diagram, all calculations can be done in ln() vs. ln() space. The advantage of this transformation is that it produces values that are free to range from −∞ to +∞. Within this infinite data space, the Euclidean distance metric can be safely applied.
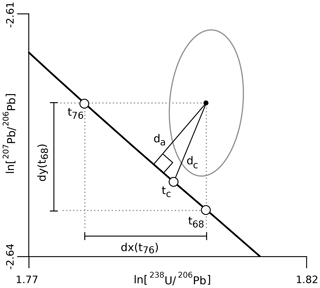
Figure 6Illustration of the two log ratio distance definitions of discordance. da is the perpendicular Aitchison distance from the measured log ratio to the concordia line. dc is the Aitchison distance measured along a line connecting the measured value and the concordia composition.
There exists a vast body of statistical literature detailing the theoretical and practical advantages of log ratio analysis. A deeper discussion of this topic falls outside the scope of this paper, but the interested reader is referred to Aitchison (1986) and Pawlowsky-Glahn et al. (2015) for further information. The Euclidean distance between log ratios is also known as the “Aitchison distance”. Discordance can be redefined as the Aitchison distance from the measured log ratios to the concordia line. We introduce two ways to do so here. A first option is to simply measure the distance along a perpendicular line to the concordia curve (Fig. 6):
where
This definition produces a parallel band around the concordia line in logarithmic Tera–Wasserburg space. In contrast with dr, dt, and dsk, the da criterion is less strict at both the young and old extremes of the geological timescale and more strict during the Proterozoic eon, when the U–Pb method is most reliable.
The perpendicular Aitchison distance criterion does not take into account the analytical precision of the isotopic measurements. To address this issue, we can also measure the Aitchison distance along a line connecting the measured log ratio and the maximum likelihood composition on the concordia line:
where sgn[*] stands for “the sign of *”, which produces positive values for measurements that plot above the concordia line and negative values for measurements that plot below it.
It is difficult to ascertain the mechanism causing discordance in any particular zircon grain. Therefore, it is unclear which of the definitions in Sects. 3 and 4 is “correct”. All we can do is apply the methods to real samples and investigate their outcomes. This section will apply the discordance filters to a dataset of 70 869 zircon U–Pb analyses that were acquired by Sensitive High Resolution Ion Micro-Probe (SHRIMP) mass spectrometry and compiled by Simon Bodorkos of Geoscience Australia.
The dataset includes 1665 sedimentary, igneous, and metamorphic samples, mostly from Australia but including some other locations as well. The data were acquired by a variety of instruments (including SHRIMP-1, SHRIMP-2, and SHRIMP-RG) using a range of different reference materials and processed on a range of different types of data reduction software (including Squid-1, Squid-2, and Prawn/Lead). The data were not subjected to any common-Pb correction or other filters and were saved in a Tera–Wasserburg format with zero error correlation between the and ratios.
Figure 7 shows the frequency distribution of the complete, unfiltered dataset as a kernel density estimate. The , , and concordia age spectra all look similar. However, the age distribution deviates from the other three chronometers. It reduces the prominence of the young age components and inflates the old end of the age spectrum.
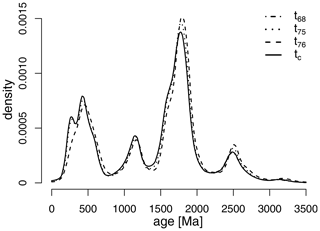
Figure 7Four superimposed kernel density estimates (KDEs, using a 50 Myr bandwidth) for 70 869 unfiltered zircon U–Pb dates. The , , and concordia age spectra are similar. However the KDE of the data stands apart from the other three curves. It deviates both at the young end of the age spectrum (which it suppresses) and at the old end (which it inflates).
Figure 8 applies five of the six discordance filters to this database (the p value filter was omitted for reasons given in Sect. 3). In order to emphasize the difference between the discordance definitions whilst treating them on an equal footing, each of the filters was adjusted until half of the data were removed. This was achieved by discordance cutoffs of Myr, %, %, %, and %.
There are noticeable differences between the density estimates. As expected from the theoretical considerations laid out in Sects. 3 and 4, the relative age filter greatly suppresses the younger age components (<1.5 Ga) relative to the older parts of the age spectrum (>1.5 Ga). The Stacey and Kramers (1975) filter has the opposite effect. It suppresses the Archaean age component by ∼50 % whilst further increasing the prominence of the Neoproterozoic and Phanerozoic modes.
The discordance definitions based on the absolute age difference and log ratio distances have a comparatively minor effect on the shape of the age spectrum. The change in shape between the age spectrum of the full (unfiltered) dataset and the age spectra of the filtered datasets can be visually assessed on quantile–quantile plots and quantified using the Kolmogorov–Smirnov (KS) statistic (Vermeesch, 2013). If the KS misfit is taken as a measure of success, then the concordia distance filter (dc) is the most effective discordance criterion. It “sharpens” the spectrum without changing the relative prominence of the modes at 400, 1200, 1800, and 2500 Ma.
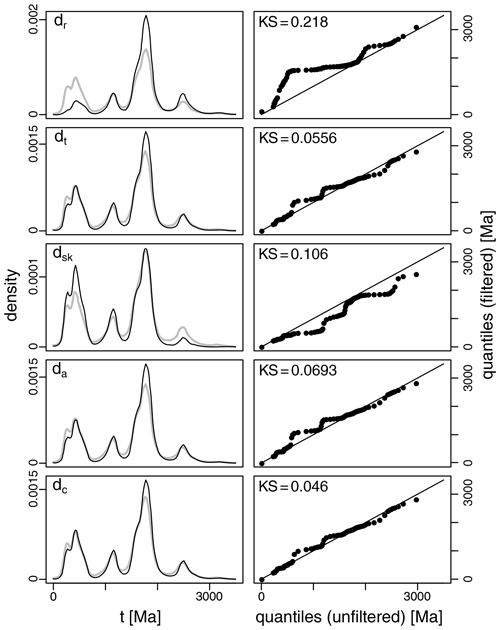
Figure 8Left: filtered U–Pb age spectra for the test data, removing the 50 % most discordant grains according to five discordance filters reviewed in this paper, shown as a kernel density estimate with 50 Myr bandwidth. The complete (unfiltered) dataset is shown in grey. Right: quantile–quantile plots comparing the filtered and unfiltered datasets. KS: the Kolmogorov–Smirnov statistic. The relative age filter (dr) introduces the greatest and the concordia distance (dc) the smallest bias.
Figure 8 removed 50 % of the data, in order to emphasize the differences between the discordance filters. In real applications, less stringent discordance filters are usually applied. As mentioned in the introduction, most current detrital zircon studies apply a 10 %–30 % relative age cutoff. Using the test data, we can evaluate the equivalent values for the dt, dsk, da, and dc criteria (Table 1). For example, a relative age filter of 10 % removes the same fraction of the test data as an absolute age filter with dt=97 Myr, a Stacey–Kramers filter with dsk=0.62 %, a perpendicular Aitchison filter with da=4.1 %, or a concordia distance filter with dc=4.6 %.
The p value discordance filter has been omitted from this comparison for two reasons. First, the use of this filter is discouraged for reasons given in Sect. 3. Second, the p value cutoffs that are equivalent to any given relative age difference are highly laboratory dependent, with precise equipment requiring different dp cutoffs than imprecise instruments. The other five discordance filters are more universally applicable. So using a different set of test data should only make a modest difference to the values in Table 1.
Table 1Conversion table for the different discordance filters, constructed using the test data. All discordance values are expressed as percentages, except for dt, which is expressed in Myr. This table allows the reader to select a discordance cutoff that removes the same fraction of their data as the relative age cutoff (dr) that they may have applied in the past.

This paper compared four U–Pb clocks and six discordance filters.
-
The clock is most precise at the young end of the geologic timescale.
-
The method is more precise than the method before the Neoproterozoic.
-
The clock offers no advantage over the previous two methods.
-
The single-grain concordia age is applicable to the entire span of geologic time and always offers the best precision. It approaches the age as time approaches zero and the age as time approaches infinity.
The six discordance filters include three existing ones and three new ones (Table 2).
-
The relative age discordance dr is the most widely used criterion today. It is more likely to remove young grains than old ones and strongly skews the age distribution towards old age components as a result.
-
The absolute age discordance dt is not widely used. But it illustrates the dramatic effect that the discordance definition can have on the filtered age distributions. Compared with the relative age filter, it is more likely to reject old grains and less likely to reject young ones. It even allows physically impossible negative ages to pass through it.
-
The p-value-based discordance filter dp may have intuitive appeal as an objective definition. But it has an undesirable negative effect on the precision and accuracy of the filtered results. It is best not to use this filter.
-
The Stacey–Kramers discordance filter dsk assumes that discordance is solely caused by common-Pb contamination. If this assumption is correct, then the dsk filter will produce the most accurate age distributions, provided that a Stacey and Kramers (1975) common-Pb correction is applied to the filtered data afterwards.
-
The perpendicular Aitchison distance da is a useful vehicle to illustrate the application of log ratio statistics to detrital zircon U–Pb geochronology. It produces a parallel acceptance zone around the (log-transformed) concordia line. This filter is most likely to reject “middle-aged” zircon grains, between 1000 and 2000 Ma, where the age-resolving power of the U–Pb method is greatest. Above and below this interval, the da criterion is more forgiving. This behaviour is desirable because natural samples tend to exhibit more age discordance below 1000 Ma and above 2000 Ma than between these dates.
-
The concordia distance dc is a modified version of the da criterion that takes into account the uncertainties of the U–Pb isotopic composition. Its effects on the U–Pb age distributions are more difficult to visualize but are similar to those of the da criterion. Applying the dc filter to the test data shows that it minimizes the difference between the unfiltered and filtered age spectra. It results in a tightening of subpopulations without changing their position or relative size. This criterion is recommended as a discordance filter.
All the discordance filters presented in this paper (both old and new) have been implemented in IsoplotR (Vermeesch, 2018), a geochronological toolbox written in the R language. Further details about this implementation are provided in Appendix B.
The uncertainty of a U–Pb date depends on three factors:
-
the age and, hence, the true isotopic ratio;
-
the sensitivity of the ion detectors to U and Pb; and
-
the dwell times used to measure the different isotopes.
These three factors vary between samples, and between labs. In order to explore their effects, let us first define the following parameters:
-
t68, t75, and t76: the , , and ages (in Ma);
-
λ38 and λ35: the decay constants of 238U and 235U (in Myr−1);
-
R85: the natural ratio;
-
R68, R75, and R76: the true , , and atomic ratios;
-
r68, r75, and r76: the measured , , and signal ratios;
-
: the fractionation factor between Pb and U;
-
: the dwell time ratio of 206Pb and 238U;
-
: the dwell time ratio of 207Pb and 206Pb;
-
n06, n07, and n38: the number of 206Pb, 207Pb, and 238U ions counted during a measurement.
Then the true isotope ratios are given by
and the measured ratios are given by
so that the predicted 206Pb and 207Pb ion counts can be written as
Assuming that all the ions are measured by secondary electron multiplier (SEM), with analytical uncertainties that are governed by Poissonian shot noise,
then the standard errors of the signal ratios are given by
Finally, the uncertainties of the age estimates are given by standard error propagation:
where
Figure 2 shows the result of these calculations using realistic values of n38, , and , which yield an outcome that is similar to the test data and to the empirical results of Zimmermann et al. (2018).
IsoplotR can be accessed either from the command line or via
a graphical user interface (GUI), either offline or online
(https://www.ucl.ac.uk/~ucfbpve/isoplotr/home/index.html, last access: 20 March 2021). The discordance
filters are accessible via both methods. In the GUI, the discordance
can be tabulated via the Age function and has also been
incorporated in IsoplotR's other functions, including its
concordia, weighted mean, and kernel density estimation algorithms.
Further details are provided under the Options menu
(Fig. B1).
To access the same functionality from the command line requires installation of IsoplotR from the Comprehensive R Archive Network (CRAN):
install.packages('IsoplotR')Once installed, the package must be added to the working environment:
library(IsoplotR)
Loading the test data into memory,
UPb <- read.data('data.csv',method='U-Pb',format=2)
The discordance can then be calculated using IsoplotR's discfilter function. For example, to compute the relative age discordance (dr),
tr <- age(UPb,discordance=discfilter(option='r'))
which produces a 70 869×9 table whose first eight columns list the , , , and concordia ages and their uncertainties and whose ninth column lists the relative age discordance as percentages. Similarly, to compute the concordia distance (dc),
tc <- age(UPb,discordance=discfilter(option='c'))
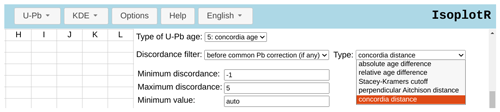
Figure B1The new discordance filters can be accessed from IsoplotR's graphical user interface, shown here under its kernel density estimation function.
Plotting a KDE of the single-grain concordia ages that pass the perpendicular Aitchison filter with %,
df <- discfilter(option='c',cutoff=c(-2,6)) kde(UPb,type=5,cutoff.disc=df)
Apply a Stacey–Kramers common-Pb correction to the data after applying a Stacey–Kramers discordance filter with %:
df <- discfilter(option='sk',cutoff=c(0,0.96)) kde(UPb,common.Pb=3,cutoff.disc=df)
If the dataset includes 204Pb (which is not the case for the test data), then we can also apply a discordance filter after the common-Pb correction. For example,
df <- discfilter(option='r',before=FALSE,cutoff=c(-5,15)) kde(UPb,common.Pb=3,type=4,cutoff.76=1200,cutoff.disc=df)
where option='r' calls the relative age filter (dr), common.Pb=3 applies a Stacey–Kramers type common-Pb
correction, type=4 uses the age for young grains and the age for old ones, and cutoff.76 marks the age (in Ma) at which to switch from the to the method. Further
information about these functions can be obtained from the built-in documentation:
?IsoplotR ?discfilter ?kde
Note that the examples shown here may take a few minutes to complete due to the large size of the test dataset.
IsoplotR is free software released under the GPL-3 license. The package and its source code are available from https://cran.r-project.org/package=IsoplotR (last access: 20 March 2021, Vermeesch, 2021). The test data can be downloaded from https://doi.org/10.5281/zenodo.4722564 (Bodorkos and Vermeesch, 2021).
The author declares that there is no conflict of interest.
The writing of this paper was triggered by a stimulating email conversation with Chris Spencer and Steve Puetz. The test data were compiled by Simon Bodorkos of Geoscience Australia, and the paper benefitted from careful reviews by Ping Wang and Keith Sircombe, with additional feedback from Chuck Magee.
This research has been supported by the Natural Environment Research Council (grant no. NE/T001518/1).
This paper was edited by Michael Dietze and reviewed by Keith Sircombe and Ping Wang.
Aitchison, J.: The statistical analysis of compositional data, Chapman and Hall, London, 1986. a, b
Bodorkos, S. and Vermeesch, P.: zircon U-Pb data compilation, Zenodo [data set], data collected or compiled by the Australian Government (Geoscience Australia), https://doi.org/10.5281/zenodo.4722564, 2021. a
Cohen, J.: A power primer, Psychol. Bull., 112, 155–159, 1992. a
Gehrels, G.: Detrital zircon U-Pb geochronology: Current methods and new opportunities, in: Tectonics of sedimentary basins: Recent advances, edited by: Busby, C. and Azor, A., Wiley Online Library, Chap. 2, 45–62, 2011. a, b, c, d
Ludwig, K. R.: On the treatment of concordant uranium-lead ages, Geochim. Cosmochim. Ac., 62, 665–676, https://doi.org/10.1016/S0016-7037(98)00059-3, 1998. a, b, c
McIntyre, G. A., Brooks, C., Compston, W., and Turek, A.: The Statistical Assessment of Rb-Sr Isochrons, J. Geophys. Res., 71, 5459–5468, 1966. a
Nemchin, A. A. and Cawood, P. A.: Discordance of the U–Pb system in detrital zircons: Implication for provenance studies of sedimentary rocks, Sediment. Geol., 182, 143–162, https://doi.org/10.1016/j.sedgeo.2005.07.011, 2005. a
Pawlowsky-Glahn, V., Egozcue, J. J., and Tolosana-Delgado, R.: Modeling and analysis of compositional data, John Wiley & Sons, Chichester, 2015. a
Puetz, S. J., Ganade, C. E., Zimmermann, U., and Borchardt, G.: Statistical analyses of global U–Pb database 2017, Geosci. Front., 9, 121–145, 2018. a, b
Schoene, B.: U–Th–Pb Geochronology, Treatise on Geochemistry, 4, 341–378, 2014. a
Spencer, C. J., Kirkland, C. L., and Taylor, R. J.: Strategies towards statistically robust interpretations of in situ U–Pb zircon geochronology, Geosci. Front., 7, 581–589, 2016. a, b, c, d, e
Stacey, J. and Kramers, J.: Approximation of terrestrial lead isotope evolution by a two-stage model, Earth Planet. Sc. Lett., 26, 207–221, 1975. a, b, c, d, e
Vermeesch, P.: Multi-sample comparison of detrital age distributions, Chem. Geol., 341, 140–146, 2013. a
Vermeesch, P.: IsoplotR: a free and open toolbox for geochronology, Geosci. Front., 9, 1479–1493, 2018. a
Vermeesch, P.: IsoplotR: Statistical Toolbox for Radiometric Geochronology, The R Foundation, available at: https://cran.r-project.org/package=IsoplotR, last access: 20 March 2021. a
Zimmermann, S., Mark, C., Chew, D., and Voice, P. J.: Maximising data and precision from detrital zircon U-Pb analysis by LA-ICPMS: The use of core-rim ages and the single-analysis concordia age, Sediment. Geol., 375, 5–13, 2018. a, b
The same calculation can also be performed in Wetherill space and is actually easier there.
- Abstract
- Introduction
- Which age should be chosen?
- Discordance filters: old definitions
- Discordance filters: new definitions
- Application to a compilation of zircon U–Pb data
- Conclusions
- Appendix A: Comparing the precision of the , , , and concordia clocks
- Appendix B: Implementation inIsoplotR
- Code and data availability
- Competing interests
- Acknowledgements
- Financial support
- Review statement
- References
The requested paper has a corresponding corrigendum published. Please read the corrigendum first before downloading the article.
- Article
(2418 KB) - Full-text XML
- Abstract
- Introduction
- Which age should be chosen?
- Discordance filters: old definitions
- Discordance filters: new definitions
- Application to a compilation of zircon U–Pb data
- Conclusions
- Appendix A: Comparing the precision of the , , , and concordia clocks
- Appendix B: Implementation inIsoplotR
- Code and data availability
- Competing interests
- Acknowledgements
- Financial support
- Review statement
- References






