Simulating sedimentary burial cycles – Part 1: Investigating the role of apatite fission track annealing kinetics using synthetic data

Age dispersion is a common feature of apatite fission track (AFT) and apatite (U–Th) $/$ He (AHe) thermochronological data, and it can be attributed to multiple factors. One underappreciated and underreported cause for dispersion is variability in apatite composition and its influence on thermal annealing of fission tracks. Using synthetic data we investigate how multikinetic AFT annealing behaviour, defined using the r_mr0 parameter, can be exploited to recover more accurate, higher-resolution thermal histories than are possible using conventional interpretation and modelling approaches. Our forward model simulation spans a 2 Gyr time interval with two separate heating and cooling cycles and was used to generate synthetic AFT and AHe data for three different apatite populations with significantly different annealing kinetics. The synthetic data were then used as input for inverse modelling in the Bayesian QTQt software to recover thermal-history information under various scenarios. Results show that essential features of the dual peak thermal history are captured using the multikinetic AFT data alone, with or without imposed constraints. Best results are achieved when the multikinetic AFT data are combined with the AHe data and geologic constraint boxes are included. In contrast, a more conventional monokinetic interpretation that ignores multikinetic AFT behaviour reproduces all the input data but yields incorrect thermal-history solutions. Under these conditions, incorporation of constraints can be misleading and fail to improve model results. In general, a close fit between observed and modelled parameters is no guarantee of a robust thermal-history solution if data are incorrectly interpreted. For the case of overdispersed AFT data, it is strongly recommended that elemental data be acquired to investigate if multikinetic annealing is the cause of the AFT apparent age scatter. Elemental analyses can also be similarly useful for broadly assessing AHe data. A future companion paper (Issler et al., 2021) will explore multikinetic AFT methodology and application to detrital apatite samples from Yukon, Canada.

1 Introduction

Studies focusing on upper crustal tectonics, landscape evolution, and sedimentary basin analysis often rely on apatite fission track (AFT) and apatite (U–Th) $/$ He (AHe) low-temperature thermochronology to decipher spatial patterns of exhumation and burial through time (e.g., Zeitler et al., 1982; Naeser et al., 1989; van der Beek et al., 1995; House et al., 1998; Ehlers and Farley, 2003). These low-temperature techniques typically produce internally consistent results in rapidly cooled, actively eroding mountain belts (e.g., Glotzbach et al., 2011). However, thermochronometric harmony commonly breaks down in slowly cooled or partially reheated settings. There are gaps in our knowledge of how fission tracks anneal in apatite (e.g., Ketcham, 2019), how ⁴He diffusion occurs over geologic time (e.g., McDannell et al., 2018), and if the mechanisms controlling these processes are fundamentally different, linked, or interact in complex and unforeseen ways (McDannell et al., 2019a). Poorly understood compound variables, both geological and analytical, sometimes yield apatite thermochronology data that are not straightforward to interpret – suggesting there are unexplained complexities present in both the AFT and AHe systems.

The canonical temperature sensitivity for AFT dating is ∼ 60–120 ^∘C (Gleadow and Duddy, 1981) and ∼ 45–75 ^∘C for AHe dating (Wolf et al., 1998). However, temperature sensitivity varies as a function of multiple factors such as apatite chemistry (Green et al., 1985, 1986; Crowley et al., 1990; Ravenhurst et al., 2003; Carlson et al., 1999; Barbarand et al., 2003) and cooling rate for AFT, and radiation damage accumulation, grain size, parent nuclide zoning, and chemistry for AHe (e.g., Farley, 2000; Shuster et al., 2006; Gautheron et al., 2009, 2013; Djimbi et al., 2015; Recanati et al., 2017). For example, AFT < AHe “age inversion” (e.g., Belton et al., 2004; Fitzgerald et al., 2006; Flowers and Kelley, 2011) is regularly encountered in continental interiors and has been attributed to the effects of slow cooling and accumulated radiation damage on He diffusion (e.g., Green et al., 2006). Ancient, slowly cooled terranes also yield highly overdispersed AFT data (e.g., McDannell et al., 2019a). This overdispersion may be due to heterogeneous apatite chemistry (e.g., O'Sullivan and Parrish, 1995), nuances of laser ablation AFT data collection and measurement precision (Vermeesch, 2017; McDannell, 2020; Cogné and Gallagher, 2021), and/or insufficient constraints on track annealing behaviour over long timescales (McDannell et al., 2019a). Alpha-radiation damage may also play a role in modifying apatite fission track annealing kinetics (Carpéna et al., 1988; Hendriks and Redfield, 2005; McDannell et al., 2019a; Li et al., 2021) or perhaps cause reduced thermal annealing resistance in apatite from old rocks. This is a debated issue (Kohn et al., 2009) requiring further scrutiny and experimental work to verify empirical relationships (e.g., Carpéna and Lacout, 2010; Li et al., 2021). These collective observations warrant a closer inspection of apatite chemistry, radiation damage, and fission track annealing for low-temperature thermochronometry and thermal-history analysis.

2 Motivation

There is clear experimental documentation that AFT annealing is influenced by composition (e.g., Gleadow and Duddy, 1981; Green et al., 1986; Carlson et al., 1999; Barbarand et al., 2003; Ravenhurst et al., 2003). While the use of track annealing kinetic models based on different apatite compositions is not a new concept (e.g., Green, 1992), there has been limited application within the broader thermochronology community over the years in terms of fully exploiting detailed apatite elemental analyses rather than kinetic proxy data. The work of Carlson et al. (1999) remains one of the most detailed studies of fission track annealing with respect to apatite chemistry. They derived the empirical r_mr0 kinetic parameter by characterizing track annealing with respect to chemical composition to produce a multikinetic annealing model that relates one apatite to another for the purposes of comparing annealing behaviour at laboratory timescales. Laboratory annealing was then extrapolated to the geologic timescale for the purpose of time–temperature (t–T) modelling (Ketcham et al., 1999, 2007). Specifically, r_mr0 is the reduced fission track length of the more resistant apatite at the point in time and temperature where the less resistant apatite is totally annealed, allowing a direct comparison between any two apatites (Ketcham et al., 1999). Therefore, r_mr0 values approaching one signify lower retentivity, whereas those approaching zero are more retentive, with common fluorapatite defined by an r_mr0 value of 0.83.

The main purpose of this paper is to show that multikinetic AFT samples with significantly different annealing characteristics carry far more thermal-history information than single AFT populations with typical annealing temperatures (∼ 100–110 ^∘C), and under certain circumstances, it is possible to recover information about multiple heating events from a single multikinetic AFT sample. Here, we present simple examples demonstrating this point using synthetic AFT data derived from forward models utilizing the r_mr0 kinetic parameter based on apatite composition (Carlson et al., 1999; Ketcham et al., 1999). The synthetic data are characterized by endmember kinetics that are rare, but not unheard of, in crystalline basement samples and more commonly encountered in detrital samples with mixed sources. This was done to illustrate that multikinetic AFT samples can provide an expanded range in thermal sensitivity and demonstrate that statistically valid, yet spurious, thermal histories may be recovered if potential kinetic sub-populations governed by composition are not accounted for during data interpretation or are alternatively unresolvable due to collection of low-precision kinetic data (Issler et al., 2018; Schneider and Issler, 2019) such as D_par (mean etch-figure diameter parallel to the c axis; Donelick, 1993).

We chose a deep-time problem involving slow cooling and multiple reheating events because it is harder to deal with than a Phanerozoic case that may have more geological constraints available. In general, deep-time problems suffer from greater uncertainty that could be addressed by having thermochronometers with a broad range of temperature sensitivity (McDannell and Flowers, 2020). This is a synthetic resolution test and a single example drawn from a nearly infinite number of possibilities. These exercises were performed assuming that we knew the true thermal history, which is almost always not the case, and they are ultimately meant to encourage users of low-temperature thermochronology to thoroughly interpret data and explore kinetics before undertaking thermal-history simulations.

For natural samples, complicated thermal-history information may be retained in multikinetic AFT data. Consideration of kinetics is most important for histories involving persistence at, or reheating to, a temperature range that differentiates the thermal response of the grains present, and thus the apparent ages and lengths recorded. Our ability to resolve kinetic populations depends on the number of AFT age and length measurements and their distribution across different populations. For example, multikinetic AFT data with low-U apatite grains can pass the X² test due to large uncertainties on single-grain apparent ages, and these can be misinterpreted as single populations if not carefully investigated using elemental data. If compositional zoning is present, apatite grains can be assigned to the wrong kinetic population (i.e., microprobe spot is not representative), or some populations may be too highly track retentive (or vice versa) to be sensitive to key parts of a thermal history. To be clear, not all natural samples are multikinetic, and the ability to retain a record of a complex thermal history depends strongly on the relative timing and magnitudes of different thermal events; this in turn feeds back into whether kinetic populations have experienced enough differential annealing to be clearly resolved. The results in this paper give us confidence in our treatment of real data and support the idea that the multikinetic AFT approach yields higher-resolution thermal histories than the conventional method. We will specifically discuss elemental data collection, multikinetic workflow and interpretation schemes, and thermal-history analysis of natural detrital samples from Yukon, Canada, in a future companion paper (Issler et al., 2021).

Unlike AFT, there is limited empirical evidence to suggest ⁴He diffusivity is strongly affected by apatite chemistry (e.g., Warnock et al., 1997; Gautheron et al., 2013; Recanati et al., 2017), whereas ab initio modelling (e.g., Djimbi et al., 2015; Recanati et al., 2021) suggests some effect. None of the diffusion studies (e.g., Warnock et al., 1997) show a direct connection between changes in diffusivity and apatite composition, but their results indicate hypothetical offsets in temperature sensitivity between compositional endmember apatites. The development of a model to explain radiation damage effects on He diffusivity (Shuster and Farley, 2009; Shuster et al., 2006) resulted in the Radiation Damage Accumulation and Annealing Model (RDAAM; Flowers et al., 2009) that used the r_mr0 parameter and fission track annealing kinetics of Ketcham et al. (2007) as a proxy for α-damage or bulk radiation damage annealing. The fundamental assumption is that α-damage and fission track damage anneal at about the same rate, enabling the use of the r_mr0 parameter in the RDAAM set to typical fluorapatite kinetics (r_mr0=0.83). This allows a comparison between fission track and AHe data within the same kinetic framework.

Many modern studies include both AFT and AHe data, and reconciliation of these complementary datasets is often difficult in slowly cooled settings. In situations where this occurs, AHe apparent age scatter is often attributed to the effects of radiation damage (or secondarily grain size), yet unexplained dispersion often persists even when these variables are considered. The commonly implemented kinetic models for the AHe system (Flowers et al., 2009; Gautheron et al., 2009) utilize fission track annealing as a proxy for radiation damage annealing – therefore it is unclear whether chemistry truly affects He diffusion or if this is illusory due to the use of a composition-based fission track kinetic model. The assumption here is that apatite chemistry does in fact influence diffusivity and that the r_mr0 parameter adequately describes radiation damage annealing in most geologic settings. Gautheron et al. (2013) and Powell et al. (2020) successfully adopted the approach of varying r_mr0 to investigate AHe age dispersion in natural samples from the Paris Basin in France and Mackenzie Plain in northern Canada, respectively. We corroborate this and show that AHe ages from grains of identical size and U content may still be highly dispersed due to differences in r_mr0 values – implying that apatite composition may be an additional source of dispersion that is mostly unaccounted for in routine applications. In in the absence of retentivity information for the AHe system, using a default fluorapatite r_mr0 value may yield “acceptable” t–T solutions that are inaccurate, especially when data containing more thermal-history information, such as AFT ages and lengths, are not collected or jointly modelled.

3 Forward and inverse modelling of multikinetic synthetic data

3.1 Forward modelled synthetic AFT and AHe data from a predetermined thermal history

Synthetic AFT data were generated from forward modelling a two-pulse heating history over 2000 Myr using the QTQt software v. 5.7.3 (Gallagher, 2012) implementing Ketcham et al. (1999) annealing kinetics (Fig. 1), with one maximum heating event occurring at 1000 Ma (110 ^∘C) and the other at 300 Ma (60 ^∘C). AFT ages and track length data (Fig. 2) were randomly predicted for three kinetic populations as external detector method (EDM) data in QTQt. In this paper, we utilized the published correlation (given in Fig. 7 of Ketcham et al., 1999) between r_mr0 (derived from electron microprobe data; Carlson et al., 1999) and measured Cl to calculate an “effective Cl” (eCl) value in atoms per formula unit (apfu) (see McDannell et al., 2019b, for further explanation). Effective Cl is the Cl concentration required to yield an equivalent r_mr0 value for the Ketcham et al. (1999) annealing model. Low-retentivity apatite with r_mr0 values exceeding the 0.84 limit of the Ketcham et al. (1999) model become negative eCl values due to extrapolation. The eCl value (e.g., Issler et al., 2018; McDannell et al., 2019b) is used to transform the nonlinear r_mr0 parameter to a linear form for data interpretation using the rearranged equation of Ketcham et al. (1999):

$$\begin{array}{}\text{(1)}& \mathrm{eCl}={\displaystyle \frac{\left(\ln \left(\mathrm{1}-r_{\mathrm{mr}\mathrm{0}}\right)+\mathrm{1.834}\right)}{\mathrm{2.107}}}.\end{array}$$

We specified three AFT kinetic populations of 10 age grains each, increasing in retentivity with r_mr0 values of 0.882 (eCl = −0.144 apfu), 0.820 (eCl = 0.057 apfu), and 0.263 (eCl = 0.726 apfu) using individual-fit c-axis-projected length kinetic data for distinct apatites from Ketcham et al. (1999). Population one is set to the Holly Springs (Georgia, USA) hydroxyapatite r_mr0 that typifies the lowest calculated retentivity in the Carlson et al. (1999) dataset, population two uses Durango apatite kinetics (laboratory age standard), whereas population three is set to Tioga (Pennsylvania, USA) Fe–Cl apatite, which is characterized by high retentivity and is an outlier of the Carlson et al. (1999) r_mr0-fitting dataset. The specified thermal history produced three AFT model ages of 670, 843, and 1602 Ma (Fig. 2). Seventy-five tracks were generated for each kinetic population with mean c-axis-projected track lengths (MTL; see Fig. 2) of 13.32 ± 1.33 µm (1σ), 14.24 ± 1.42 µm, and 14.65 ± 1.47 µm, respectively. The initial (pre-annealed) track lengths (l_oc) for each kinetic population were calculated as 16.17, 16.40, and 17.16 µm with increasing retentivity and were estimated from the equivalent D_par calculated from the indicated r_mr0 value for each kinetic population using the l_oc–D_par relation from Carlson et al. (1999). Three AHe ages were also forward modelled using the RDAAM of Flowers et al. (2009), which implements the Ketcham et al. (2007) kinetics for radiation damage annealing. We applied Holly Springs, typical endmember fluorapatite (r_mr0=0.83 and the RDAAM default), and Tioga apatite r_mr0 values to AHe grains, all with spherical grain radii of 50 µm and 25 ppm U (Th and Sm discounted for simplicity). The uncorrected AHe ages (α ejection-corrected age in brackets) were 585 Ma [813 Ma], 610 Ma [848 Ma], and 819 Ma [1139 Ma] predicted using the same t–T history (Fig. 1) as the AFT data.

Figure 1 Thermal history used to predict synthetic AFT and AHe data. This t–T path is referred to as the “true” thermal history throughout this paper. The predicted synthetic data were then used as input for QTQt to recover the thermal history through inverse modelling. PAZ: partial annealing zone for fission tracks.

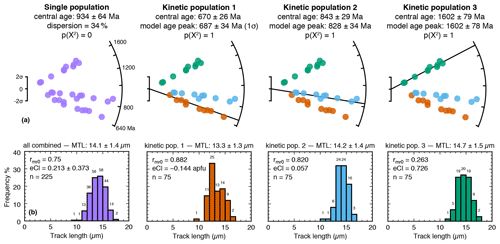
Figure 2 Predicted synthetic AFT data from the thermal history in Fig. 1. Multikinetic age populations were individually predicted using distinct r_mr0 kinetics shown in (b) panels (discussed in the text). These data were then input in QTQt and inverted to recover the true thermal history in Fig. 1 (see Fig. 3). (a) Central age and 1σ errors are indicated for each kinetic population. Throughout this paper, “central age” is used for historical reasons to refer to the approximate geometric mean of a population of single-grain AFT ages (Galbraith and Laslett, 1993). The first radial plot shows all 30 individual grains and demonstrates that when taken together, the combined sample fails the X² test (p < 0.05) for homogeneity (i.e., that all grains belong to a single underlying age population). This suggests the presence of multiple age populations and is the scenario most researchers would start with before evaluating the sample for potential multikinetic behaviour. Mixture modelling was subsequently performed on the combined sample, and the model age peaks that were picked seamlessly align with the individual kinetic population central ages. Kinetic populations one, two, and three are displayed as arms on their respective radial plots, with individual AFT ages closer to the origin being less precise. This aligns with how model populations would be selected and compared with the elemental chemistry for individual age grains during multikinetic interpretation for natural samples (see Schneider and Issler, 2019; McDannell et al., 2019b). (b) The predicted track length distributions for the combined and individual kinetic populations derived from the thermal history in Fig. 1 using the specified kinetic parameter value. Numbers on the histogram are the number of tracks in each 1 µm bin. Abbreviations: eCl – effective Cl; MTL – mean track length.

3.2 Methods for inverting AFT and AHe synthetic data for thermal history

We attempted to recover the true thermal history used to predict the synthetic data from Sect. 3.1 using the QTQt software. QTQt implements a reversible jump Markov chain Monte Carlo algorithm to systematically search t–T space (Gallagher, 2012). These exercises imitate real thermal-history investigation in the context of incomplete geologic knowledge, complex or imperfect datasets, and judgement calls that are typically made by researchers implementing thermochronology data and performing modelling to infer quantitative information about geologic processes. We also explore the consequences of neglecting the identification of multikinetic populations during AFT modelling and the effects of kinetic assumptions for AHe ages. An important point is that QTQt uses the ratio of data fit, or likelihood, between a current and proposed model. Candidate thermal histories that predict the data adequately (in relation to the current thermal history) can be accepted, regardless of geological feasibility; therefore it is up to the user to understand the ramifications of this and make sensible decisions about modelling input and output (Vermeesch and Tian, 2014; Gallagher and Ketcham, 2018). Conversely, other software such as HeFTy (Ketcham, 2005) or AFTINV (Issler, 1996) implement a nondirected Monte Carlo (MC) search algorithm and an absolute approach using the p value as a threshold measure of satisfactory statistical fit. We used QTQt because it is sensitive to the number and quality of data during history inference (i.e., notionally improving model results with additional, high-quality data) and specifically because it will accept model histories regardless of the physical plausibility of a history simulation – this was done to explore the possible effects of improper data treatment or data misinterpretation.

The r_mr0 values for AFT and AHe data were held fixed for simulations. In QTQt, AFT central ages are not used directly during model prediction; instead random sampling of the spontaneous and induced (N_s + N_i) track counts and track densities are used for fitting (see Appendix A of Gallagher, 1995, for more details on AFT age prediction). The track length data are generated by drawing the desired number of lengths randomly from the predicted distribution (Gallagher, 1995). The individual kinetic populations are underdispersed with respect to natural samples, but apparent age dispersion is high for the overall sample – which is the normal starting condition for most natural samples that then require further interpretation. The AFT central age and uncertainty are insensitive to the kinetic population underdispersion, and this does not affect modelling outcomes.

The data were formulated with identical EDM parameters, including, a ζ-calibration value = 350 yr cm⁻², induced track density (${\mathit{\rho }}_{D_{\mathrm{i}}})=\mathrm{2.5}\times {\mathrm{10}}^{\mathrm{6}}$ cm⁻², and dosimeter tracks (N_d) = 10 000. These common parameters made it so that each population was simulated as being from the same grain mount for the purposes of easy comparison and t–T inversion. The synthetic AFT sample has an overall central age of 934 ± 64 Ma (1σ; (P)X²=0.0; 34 % dispersion; n = 30) when all age grains are combined. The central AFT age for population one was calculated as 670 ± 26 Ma, population two was calculated as 843 ± 29 Ma, and population three was calculated as 1602 ± 79 Ma. Three mixture model age peaks of 687 ± 34 Ma, 828 ± 34 Ma, and 1602 ± 78 Ma (1σ) were selected in IsoplotR (Vermeesch, 2018) for the combined AFT data and agree with the individual kinetic population central ages. The uncorrected AHe ages were modelled with all default RDAAM settings with the exception of r_mr0 and input as 585 ± 17, 610 ± 18, and 819 ± 25 Ma (1σ), with typical analytical uncertainties for (U–Th) $/$ He apparent ages.

We ran QTQt in multiple stages to tune the parameters for sampling and to ensure the acceptance rates for time and temperature were between ∼ 0.1–0.7, within the acceptable limits discussed in Gallagher (2012). Inversions were run for > 500 000 to > 1 000 000 total iterations (burn-in and post burn-in) and were considered complete when the likelihood distribution was stationary (i.e., there was no trend in the likelihood values with a stable or “flat” mean; Gallagher, 2012). The modelling t–T space (general prior) was designated as 1000 ± 1000 Ma and 150 ± 150 ^∘C with a maximum allowed heating–cooling rate of 5 ^∘C Myr⁻¹. Sampling proposed outside of the prior was prevented, and more complex models were rejected for proposed models of equivalent likelihood. Therefore, t–T points were only accepted if they provided a better fit to the input data, which is a newer feature in QTQt that essentially prevents overly complex model paths from being accepted if they do not provide any benefit or improvement in data fit.

The long time interval for these model inversions are styled after a typical cratonic history, and the only constraint that was consistently enforced was starting the model at 300 ± 1 ^∘C at 2000 ± 1 Ma. For our purposes, this scenario is considered a “no constraint” model since we apply this as a starting condition for all inverse models well above the sensitivity of our thermochronology data. We also ran models that enforced constraint boxes (i.e., with either one or two boxes) at 20 ± 10 ^∘C at 1650 ± 100 Ma and 20 ± 10 ^∘C at 500 ± 50 Ma, requiring t–T paths to pass through them. These t–T boxes were treated as “known” geologic information for the inversions and represent common geologic situations for cratons with Proterozoic and Phanerozoic basement nonconformities. However, these boxes purposefully represent an incomplete period at surface conditions with respect to the true thermal history, the repercussions of which will be discussed below in Sect. 5.2.

For all models presented hereafter, we show the QTQt maximum likelihood (ML; i.e., usually more complex, best fit t–T path to the observed data, red line) and expected models (EX; i.e., ∼ weighted mean of the posterior distribution ±95 % credible interval; black lines) with respect to the true thermal history (white line) used to predict the synthetic data (Fig. 1). In our thermal-history plots, the individual t–T paths are coloured by [log] path density, which is proportional to the relative probability, with higher-intensity (brighter) colours denoting higher path density and higher relative probability. Note that in Bayesian inference, the posterior probability is proportional to the likelihood multiplied by the prior, and in QTQt the prior acts as a penalty against making the model too complex and thus the maximum posterior (MP) model will commonly be the simpler t–T path when compared to the ML path (i.e., equal to or fewer than t–T points; Gallagher, 2012). We have excluded the MP model for plot clarity for most output because the ML and MP paths are identical or nearly so for most scenarios, which implies a well-sampled and constrained ensemble of solutions (Gallagher and Ketcham, 2020).

4 Model inversion results

QTQt inversion results are shown in Fig. 3 and illustrate the implications of multikinetic AFT-only, joint models with multikinetic AFT and AHe grains using the correct kinetics (i.e., the kinetics implemented during forward modelling to predict AHe ages), and different combinations of incorrect monokinetic AFT models where the three multikinetic populations were combined and treated as a single AFT sample, and/or AHe ages were assumed to have the endmember fluorapatite r_mr0 value. Figure 4 depicts the results comparing observed synthetic data and model predictions for the inversions in Fig. 3. The first three models are “multikinetic AFT-only” models (Fig. 3a–c), whereas the second row of models depicts results for three multikinetic AFT populations and three AHe grains (Fig. 3d–f). The last three panels are the single-population AFT models (Fig. 3g–i). To reemphasize, we prevented t–T points from being accepted during QTQt inversions unless the addition of points provided better agreement between observed and predicted data. Therefore, all of our preferred results and discussion focus on the ML model t–T path since this path is the best fit to the data and is, in these instances, not unnecessarily complex, yet we show the EX model and 95 % credible interval for comparison and to provide a general picture of the overall model ensemble.

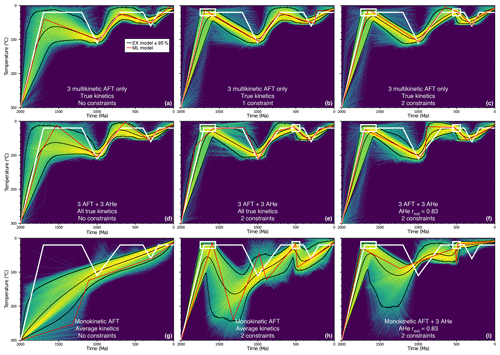
Figure 3 Thermal-history inversion results from QTQt under different imposed kinetic and t–T assumptions. Relative probability is proportional to (log) path density in our t–T figures; therefore brighter colours (or higher saturation) denote higher relative probability. Panels (a)–(c) show the “AFT-only” models that utilized three multikinetic AFT populations (discussed in the text) as the only input data. The true r_mr0 kinetics applied during forward modelling were entered in the input files and held fixed for each kinetic population during the inversion. Panels (d)–(e) show the results of models that correctly utilized three multikinetic AFT kinetic populations and three AHe ages all with the true kinetics held fixed. Panel (e) is the best model inversion incorporating all correct thermochronometer information used during forward modelling of the synthetic dataset. The panel (f) model was completed under the same conditions as panels (d)–(e) except that the three AHe grains all employ the incorrect (in the oldest and youngest cases) RDAAM default fluorapatite r_mr0 value of 0.83 as the kinetic parameter. Panels (g)–(i) were modelled assuming a “monokinetic” or traditional single-population AFT sample that combines all three multikinetic populations into one. For all panels, the thick white line is the “true” thermal history from Fig. 1; red lines are the maximum likelihood model (best fit) t–T path from QTQt; black lines are the expected model t–T path and 95 % credible interval. Assumed t–T constraints are white boxes that require thermal histories to pass through them during the inversion.

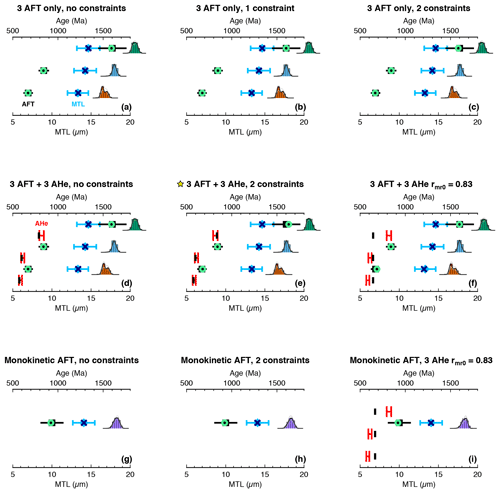
Figure 4 QTQt inversion predictions compared to “observed” synthetic thermochronology data generated during forward modelling. Panel letters correspond to counterpart t–T model panels in Fig. 3. All predictions are for the maximum likelihood models. Squares are observed AFT central age ±2σ, circles are predicted AFT age, diamonds are observed MTL ±1σ, and X symbols are the predicted MTL. Individual model fits to each track length distribution for the AFT kinetic populations are also shown and colour-coded the same as Fig. 2. Observed apatite He ages shown by red H symbol (spans the 1σ error range quoted in the text) and predicted AHe ages are black bars. Panel (e) with star is our best model that accounts for all multikinetic AFT populations and utilizes the true AHe kinetics and two geologic constraints, all combined for the highest thermal-history resolution. Note that track length distributions are arbitrarily placed next to their respective age population and were not plotted with respect to the MTL plot axis.

4.1 AFT-only models – identified multikinetic age populations and correct kinetics

The first model was setup to simultaneously invert each AFT kinetic population without AHe data for scenarios with a “no constraint” model, a “single t–T constraint” model, and “two t–T constraints” model (Fig. 3a–c). These simulations were meant to be the ideal case using a lone AFT chronometer with extended thermal sensitivity due to the presence of multikinetic apatite populations. We investigated the ability to recover the true thermal history using properly identified kinetic age populations while utilizing the fixed, true r_mr0 value from forward modelling for each population under varying degrees of geologic assumptions or constraints. The general shape, timing, and magnitude of the true history form and peak temperatures are recovered for the multikinetic AFT models regardless of whether constraint boxes were used. This suggests to us that the combination of high quality, distinct age, and length populations enhance t–T history resolving power, which becomes progressively improved if kinetic populations sample a broad range of kinetic space (predicted AFT parameters closely agree with the synthetic data; Fig. 4a–c).

4.2 AFT + AHe models – consequences of the r_mr0 parameter

The addition of the three AHe ages using their correct kinetics (i.e., r_mr0 values) along with the three multikinetic AFT populations (Fig. 3d) marginally improved thermal-history recovery with respect to the AFT-only models (Fig. 3a–c), while the addition of two constraint boxes produced a ML model t–T path that reproduced nearly all features of the true thermal history (Fig. 3e). Figure 3e is the best thermal-history model that utilized all assumptions and information used during forward model generation of the synthetic dataset and provides the closest fit to the synthetic data (Fig. 4e). Setting all three AHe grains to 0.83 r_mr0 produces distortion of the ML model history with respect to the true history (Fig. 3f). The model predicts three AHe ages that are virtually identical but provides a poor fit to the input synthetic AHe ages (Fig. 4f). The 610 Ma AHe grain (true kinetic r_mr0 value = 0.83) was on the margin of acceptability. However, in this case the overall group of model paths is still similar to the other “AFT-only” and “correct kinetics AHe” models simply because the multikinetic AFT populations are the primary controls on the t–T history. The AFT data contain more t–T information and exert more influence, and without them, the model ensemble would instead be highly inaccurate (e.g., Fig. 3i; see below).

4.3 Monokinetic AFT models – incorrectly combined kinetic populations

In our experience, multikinetic behaviour is not uncommon for basement samples characterized by complicated burial histories and nearly always present for detrital apatite samples derived from complex source areas that experience multiple heating events. In our “monokinetic” scenario, the multikinetic AFT data were incorrectly treated as a single population and modelled using the central age, MTL, and average eCl (or r_mr0)  ± 1σ of the entire pool of synthetic single-grain ages. As previously mentioned, combining the three populations caused the sample to fail the chi-square test (P(X)²=0.0), and the calculated AFT central age was 934 ± 64 Ma, the overall MTL was 14.07 ± 1.40 µm (n = 225), and the average eCl is 0.213 ± 0.373 apfu for all grains (equivalent r_mr0 ≈ 0.75). AFT data are usually treated as such in the published literature, and overdispersed data are often modelled regardless of the X² statistic. This situation could conceivably occur when the three kinetic populations were either ignored or there was insufficient kinetic parameter resolution to identify discrete kinetic groups. A sample could also simply not be multikinetic – but the models here are meant to illustrate the hazards of monokinetic misinterpretation for thermal-history analysis. In the monokinetic simulation without constraints, both the ML and EX t–T paths do not accurately reproduce the true thermal history (Fig. 3g). In this instance the ML path simply passes through both true thermal maxima and yet yields excellent fits to the observed synthetic data (Fig. 4g). The addition of two constraint boxes produced even more complex and highly inaccurate t–T solutions (Fig. 3h) and reproduced well the observed AFT data (Fig. 4h). The AFT sample was modelled as monokinetic again but also included the three AHe ages using a uniformly applied default RDAAM r_mr0 value of 0.83 for each apatite grain (Fig. 3i). This was done to provide further insight into whether this combination could yield a better outcome just from the addition of more data for the inversion. The EX model is still inaccurate, but the addition of AHe grains made the ML path simpler; nevertheless it poorly reproduces the true thermal history. The true AHe apparent ages were not well reproduced, and the same age was predicted for all three grains (Fig. 4i). This may be because the second 610 Ma AHe grain utilized the true r_mr0 value of 0.83 from the forward modelling and was the best-predicted age of the three (close to the observed age upper uncertainty limit) and dominated the iterative sampling during the inversion. The AHe kinetics produced forward model ages that were distinctly older (819 Ma) and younger (585 Ma) than the (middle) 610 Ma grain, but these were unable to be reproduced assuming incorrect r_mr0 kinetics.

5 Discussion

5.1 Apatite composition and multikinetic interpretation

The AFT and AHe modelling results presented here may seem intuitive based on the implemented kinetics and modelling exercises using synthetic data but are worth discussing, since situations where variable apatite compositions could influence thermochronometric ages are likely to be encountered in natural samples. The results indicate the benefits offered by interpreting intrasample AFT kinetic populations for inverse modelling and show how inappropriate assumptions regarding kinetic parameters can greatly influence model outcome. Our examples were determined for a single, distinct thermal history, and yet they establish that apatite composition and multikinetic interpretation (when appropriate) provide valuable information for thermal-history modelling – and they are mostly unexplored, or at least underutilized, by routine AFT studies.

Collection of elemental data and interpretation of multikinetic samples is particularly important for providing greater t–T resolution (Fig. 3a–f), whereas combining or overlooking kinetic populations effectively smears the t–T signal contained in the individual kinetic groups and produces a meaningless hybrid thermal-history model (Fig. 3g–i). We could disregard these incorrect model simulations as self-fulfilling due to forward modelling a synthetic dataset and assuming “perfect” kinetic models; however for real scenarios we would not know the true thermal history, and without other information, this class of results could be interpreted as geologically meaningful. Perhaps more important are the broader implications for thermal-history modelling if there are inappropriate assumptions regarding data interpretation and certain steps are not taken to fully evaluate AFT samples (Fig. 3g–i), especially at longer timescales where there is greater uncertainty and less geologic control. An important point is that if multikinetic populations exist and are properly interpreted, they have the potential to constrain a much broader range of t–T space than an incorrect monokinetic (single population) interpretation for an overdispersed AFT sample. Many readers may appreciate that assuming or inadvertently “forcing” the wrong model is a problem, but this remains a highly reviewed topic (e.g., Vermeesch and Tian, 2014; Fox et al., 2019) and is seemingly underexplored in studies, as multikinetic-focused literature utilizing detailed elemental chemistry remains practically negligible in the > 20 years since multikinetic models were introduced. Gallagher and Ketcham (2020) also touch on these points in response to the lengthy modelling discussion sparked by Vermeesch and Tian (2014), and these are the primary themes of this work.

5.2 Data quality and kinetic parameter influence on t–T resolution

The overall temporal and thermal resolution contained in multikinetic AFT data is influenced by multiple factors, such as the amount and distribution of the data (i.e., if most of the data are contained in one population versus distributed more equally), thermal history (i.e., the magnitude and sequence of heating-cooling events), and kinetics (i.e., the range of temperature sensitivity). A greater number of different kinetic groups are sensitive to an expanded t–T range than a single population. However, the ability to recover thermal-history information depends on the details of the thermal history; if maximum temperatures occur late in the history, then previous events are thermally overprinted, and the early history is obscured or erased entirely. We intentionally used an ideal synthetic dataset with well-defined kinetic populations that have an equal distribution of data across all populations. Natural populations may have an uneven distribution of grains, and therefore populations that contain the most data will best resolve distinct parts of the thermal history. Our QTQt inversions demonstrate the ability of these data to inform t–T modelling in the context of variable kinetics and different modeller assumptions. The similarity between expected models that do and do not require paths to pass through explicit t–T boxes (e.g., Fig. 3a–c) is informative for general modelling practices using Bayesian inversion methods. This tells us that the multikinetic data being inverted have enough sensitivity to resolve the general t–T history without necessarily requiring explicit conditions imposed on the t–T search. This is perhaps unexpected, as the Bayesian sampling implemented by QTQt generally favours simpler models over complex ones, which is a possible deterrent for users investigating deep-time thermal histories (McDannell and Flowers, 2020). However, this should not preclude the use of QTQt for deep-time problems, as the addition of thermochronological data augments inferences regarding thermal-history complexity.

However, enforcing constraints do not provide a remedy if AFT kinetic relationships are ignored. The main region of t–T space that proved difficult to resolve in all models was the prolonged periods at low temperature. This was anticipated since the kinetic models and chronometers themselves are rather insensitive to temperatures < 50 ^∘C. The EX model may define an envelope that seems consistent with the known true history (Fig. 3a–c); however this does not take into account the form of individual thermal histories that may be inconsistent with the true history. There were individual paths that were more similar to the true history for these three simulations, yet they were considered lower relative (posterior) probability due to constraint box placement. We may expect this compromise between accuracy (i.e., closer to the true solution) and precision (i.e., greater certainty) because subsequent heating event(s) erase t–T information. The earlier or older, low-temperature parts of the history will be less and less resolvable with additional reheating and thus may require constraint boxes to focus the t–T search. However, imposing “uncertain” constraints, or constraints that do not fully capture the geologic record where the model is less sensitive, leads to exclusion of (potentially viable) solutions and tightens the 95 % credible interval. These results suggest that data quantity, quality, and the use of t–T constraint boxes variably trade off with one another, and the validity or uncertainty of geologic constraints should be carefully considered and tested for natural samples since model results are conditional on these factors.

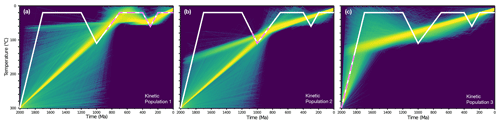
Figure 5 QTQt models of each individual AFT kinetic population plotted with respect to the true thermal history. (a) Kinetic population one. (b) Kinetic population two. (c) Kinetic population three. The magenta dashed line indicates the approximate t–T sensitivity of each kinetic population within the overall model history (also see Fig. 6b retention ages). The true kinetics were applied in each simulation. All other explicit boundary conditions are the same as previous models.

Figure 3e shows the ideal case with the most accurate thermal-history recovery (nearly identical to the true history) when two constraint boxes are implemented with three interpreted AFT kinetic populations and three AHe grains modelled using the proper kinetics. Importantly, this applies in the case of integrating multiple low-temperature thermochronometers and/or multikinetic AFT data, especially multikinetic populations that progressively diverge in kinetics, therefore increasing thermal resolution. However, constraint boxes provide no obvious advantage when the three multikinetic populations are ignored and only the overall central AFT age is modelled (Fig. 3h). We show additional QTQt models in Fig. 5 to further establish the utility of modelling AFT grain populations with different annealing kinetics and the distinct temperature sensitivity provided by each kinetic group. These simulations were carried out for each kinetic population individually to demonstrate the sensitivity of each population to the multiple heating and cooling events present in the true forward history. The model in Fig. 5a shows that population one is only sensitive to post-1 Ga cooling and the second reheating event, whereas the model in Fig. 5b shows that population two is most sensitive to peak temperatures achieved during the first heating event. Population three is sensitive to the initial cooling from high temperature and requires some poorly resolved reheating to partially reset the AFT age and match the track length distribution. The high retentivity of population 3 makes it mostly insensitive to the two heating and cooling cycles. Each of these simulations illustrates that a single AFT population lacks sufficient t–T information to adequately resolve the (entire) true thermal history, yet when each kinetic population is combined and modelled simultaneously (Fig. 3), their consolidated sensitivities enhance recovery of the true t–T solution.

Recently, Green and Duddy (2020) stated that “thermochronology data in isolation cannot define periods when samples were cooler and subsequently reheated. This can only be defined with the aid of constraints from geological evidence.” Their comment alludes to the non-uniqueness of t–T models and is true in situations where a single AFT age population is modelled, or more generally when only one thermochronometer is used to elucidate complicated t–T histories. Green and Duddy (2020) go on to state that slow, continuous cooling is often assumed in published thermal history models and that this is inappropriate. However, model simulations such as the one that we show in Fig. 3g tell us that the wrong model may imply slow monotonic cooling, although it is not outright assumed, in agreement with the comment by Gallagher (2021). We agree that monotonic-cooling solutions that faithfully reproduce observed thermochronology data (Figs. 3g and 4g) are not necessarily “correct” and are a product of attempting to recover a complex history with low-resolution data with incomplete (or absent) geologic context. However, we propose that multikinetic AFT data or, more generally, integration of independent information from multiple chronometers demonstrates that their view does not apply absolutely, as we can see illustrated in Fig. 3a. Our examples that utilize high-quality multikinetic data (Fig. 3a–e) indicate that universal slow cooling assumptions are invalid.

5.3 Comparison with nondirected Monte Carlo t–T simulation

Multikinetic AFT data may record complicated thermal histories that are difficult to simulate using classical randomized MC algorithms, and model success can depend strongly on the choice of boundary conditions that are used to limit the model search space. The synthetic AFT data were inversely modelled using the newest version of AFTINV v. 6.15 (Issler, 1996), a derivative of the Willett (1997) model that is similar to the HeFTy software (Ketcham, 2005) in using a nondirected MC scheme and p values to generate and evaluate thermal histories. Unlike HeFTy, AFTINV uses fixed, user-specified time points of arbitrary spacing and generates thermal histories by randomly selecting heating and cooling rates to calculate temperature points forward and backward in time. Thermal histories are constructed by piecewise assembly of different thermal-history styles (e.g., heating or cooling only or heating–cooling cycles) that are separated by randomly selected thermal minima within user-specified time ranges that incorporate uncertainty in the time of deposition or onset of reburial. Monte Carlo calculations are performed to obtain a set (typically 300) of solutions exceeding the 0.05 level of significance, and then a controlled random search (CRS; Price, 1977) learning algorithm is used to update the solution set to the 0.5 level. Up to four different AFT kinetic populations can be modelled simultaneously. Failure to find any solutions at the 0.5 level may indicate a problem with the boundary conditions, the style of thermal history, or incompatibilities among the kinetic populations, and further investigations should be undertaken to determine the source of the problem.

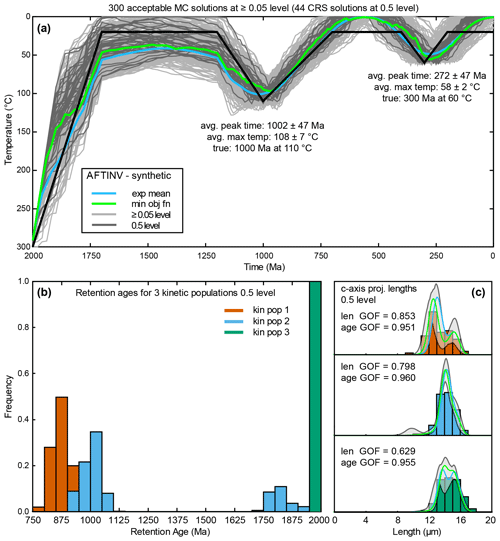
Figure 6 (a) AFTINV software thermal-history inversion results using random MC and the CRS algorithms (e.g., Willett, 1997; McDannell et al., 2019b). Model in (a) was set up to find 300 random MC solutions at the 0.05 fit level (not shown), which are then used as a “seed” pool for the CRS algorithm to iteratively recombine and refine the solution set to the better 0.5 statistical fit level. In this example, not all solutions reached the 0.5 significance level (only 44 did; dark grey lines) and are therefore ≥ 0.05 level (light grey lines). The exponential mean t–T path is shown for all 300 solutions (blue line) along with the “minimum objective function” or overall best-fit solution (green line). (b) Retention ages or hypothetical age of the oldest retained fission tracks (2 µm) for each kinetic population. Retention ages give a rough sense of temperature sensitivity. (c) Track length distribution model fits for the exponential mean and minimum objective function t–T paths for each kinetic population. Observed versus predicted goodness of fit (GOF) for AFT age and track length for the minimum objective function solution. See McDannell et al. (2019b) for further discussion of AFTINV modelling methods.

Model sensitivity runs were undertaken to determine the boundary conditions needed to obtain close fitting solutions, and Fig. 6 shows the final preferred model results obtained from the CRS calculations. We assumed two random reheating events with two accompanying thermal minima randomly selected between 1700–1200 and 700–400 Ma for the model t–T history. Previous models that used broad rate limits required millions of trial model solutions that produced a wide range of marginally acceptable solutions (0.05 level) that could not be updated by the CRS algorithm to produce the narrower thermal peaks needed to closely fit the AFT data at the 0.5 level. Limiting the heating–cooling rates to 0.2 ^∘C Myr⁻¹ from 1700 to 1200 Ma and 1 ^∘C Myr⁻¹ for the post-1200 Ma history improved model performance dramatically and yielded 44 solutions at the 0.5 significance level (dark grey lines; Fig. 6a). These limits kept temperatures closer to surface conditions prior to the first heating event and eliminated spurious temperature fluctuations associated with rates that are much higher than those used to generate the synthetic data (Fig. 1). For natural multikinetic samples, we do not know the thermal history in advance, so iterative modelling and flexible boundary conditions may be necessary to obtain good t–T solutions.

Unlike the QTQt model results of Fig. 3, all individual thermal histories in Fig. 6a provide statistically significant fits to the AFT data. The minimum objective function solution (green curve; Fig. 6a) provides the closest fit to the AFT age and length data (Fig. 6c). The exponential mean of all 300 solutions (blue curve; Fig. 6a) provides acceptable fits for kinetic populations two and three but fails to fit population one lengths due to insufficient annealing; the wide range of permissible solutions for the low-temperature peak results in an exponential mean peak temperature that is lower than each of the individual solutions. Retention ages (Fig. 6b) are model ages representing the oldest track (the shortest retained track length of ∼ 2 µm) present in each population, and they indicate the approximate times when thermal-history information is retained by each AFT population. Population one retention ages are younger than thermal peak one, implying total annealing and accumulation of new tracks after the peak one maximum temperatures. Population two shows a bimodal retention age distribution indicating that some solutions have tracks with older retention ages that were not reset during the first cycle of heating. Population three retention ages are all ∼ 2000 Ma, implying high track retentivity and insensitivity to the two heating events.

6 Conclusions

Using synthetic multikinetic AFT (and AHe data) derived from forward modelling, we show that, under favourable conditions, it is possible to extract multi-cyclic heating and cooling history information using inverse modelling methods when kinetic parameters for AFT annealing are correctly specified. Essential details of a two-phase heating and cooling history are reproduced using AFT multikinetic data alone without imposing constraint boxes, but the closest fit to the true solution is achieved using all the synthetic data with constraint boxes. Alternative monokinetic interpretations that ignore multikinetic behaviour generate solutions that significantly depart from the true solution while providing close fits to the interpreted AFT data; under these conditions, imposing constraint boxes does not improve modelled t–T solutions with respect to the true thermal history and the timing and magnitude of heating events. Within the context of our simulations and assumptions regarding helium diffusion kinetics, ignoring apatite composition (r_mr0 kinetic parameter) when it truly deviates from fluorapatite kinetics can cause observed AHe ages to be reproduced poorly and yield inaccurate model thermal histories. Therefore, if apatite composition does appreciably modify He diffusivity, this effect may be an additional, and unaccounted for, source of overdispersion in AHe datasets, and disagreement between observed and modelled ages may be due to incorrect (kinetic) model assumptions rather than poor-quality data.

We recommend the routine collection of elemental data for apatite dated using the fission track method to better quantify sample compositional variation and relate this to kinetic behaviour for thermal-history analysis. Elemental data may also prove useful to characterize first-order chemical variation in AHe datasets. The use of r_mr0, while imperfect, still provides the best resolution for kinetic interpretation when compared to other kinetic proxies. For natural samples, radial plot mixture modelling and trends between AFT data and apatite chemistry are the primary tools for multikinetic interpretation and should be approached iteratively and conservatively, and when possible, compared with other regional AFT samples and geologic data to assess applicability and consistency. The ability to recover high-resolution thermal histories from multikinetic AFT samples depends on the details of the thermal history and characteristics of the data. These topics are discussed more fully in a future companion paper (Issler et al., 2021) that examines detrital AFT samples from Yukon, Canada, to illustrate multikinetic AFT interpretation and modelling methods.