Technical note: A software framework for calculating compositionally dependent in situ ¹⁴C production rates

Over the last 30 years, in situ cosmogenic nuclides (CNs) have revolutionized surficial processes and Quaternary geologic studies. Commonly measured CNs extracted from common mineral quartz have long half-lives (e.g., ¹⁰Be, ²⁶Al) and have been applied over timescales from a few hundred years to millions of years. However, their long half-lives also render them largely insensitive to complex histories of burial and exposure of less than ca. 100 kyr. On the other hand, in situ cosmogenic ¹⁴C (in situ ¹⁴C) is also produced in quartz, yet its 5.7 kyr half-life renders it very sensitive to complex exposure histories during the last ∼25 ka, a particularly unique and powerful tool when analyzed in concert with long-lived nuclides. In situ ¹⁴C measurements are currently limited to relatively coarse-grained (typically sand-sized or larger, crushed or sieved to sand) quartz-bearing rock types, but while such rocks are common, they are not ubiquitous. The ability to extract and interpret in situ ¹⁴C from quartz-poor and fine-grained rocks would thus open its unique applications to a broader array of landscape elements and environments.

As a first step toward this goal, a robust means of interpreting in situ ¹⁴C concentrations derived from rocks and minerals spanning wider compositional and textural ranges will be crucial. We have thus developed a MATLAB^®-based software framework to quantify spallogenic production of in situ ¹⁴C from a broad range of silicate rock and mineral compositions, including rocks too fine grained to achieve pure quartz separates. As expected from prior work, production from oxygen dominates the overall in situ ¹⁴C signal, accounting for >90 % of production for common silicate minerals and six different rock types at sea level and high latitudes (SLHL). This work confirms that Si, Al, and Mg are important targets but also predicts greater production from Na than from those elements. The compositionally dependent production rates for rock and mineral compositions investigated here are typically lower than that of quartz, although that predicted for albite is comparable to quartz, reflecting the significance of production from Na. Predicted production rates drop as compositions become more mafic (particularly Fe-rich). This framework should thus be a useful tool in efforts to broaden the utility of in situ ¹⁴C to quartz-poor and fine-grained rock types, but future improvements in measured and modeled excitation functions would be beneficial.

1 Introduction

Rare nuclides produced in situ in minerals near the Earth's surface by cosmic-ray bombardment (in situ cosmogenic nuclides or CNs) have revolutionized studies of geomorphology and Quaternary geology. CNs build predictably over time in an exposed surface through nucleon spallation and muon reactions (e.g., Gosse and Phillips, 2001). As such, the time at which geomorphic surfaces formed by glacial, fluvial, or marine activity can often be constrained with CNs, an application known as surface exposure dating. In addition, CNs can be used to constrain rates of surficial processes with appropriate interpretive models. These applications rely on measuring the concentrations (atoms g⁻¹, hereafter at g⁻¹) of CNs in a sample and calculating an exposure age or erosion rate based on the production rate (at g⁻¹ yr⁻¹). The most commonly measured CNs, ¹⁰Be ($t_{\mathrm{1}/\mathrm{2}}$ 1.39 Myr; Korschinek et al., 2010; Chmeleff et al., 2010) and ²⁶Al ($t_{\mathrm{1}/\mathrm{2}}$ 0.705 Myr; Nishiizumi, 2004), are typically extracted from quartz due to its simple composition and corresponding resistance to weathering under a wide range of environmental conditions. Their long half-lives make these nuclides useful in dating surfaces that have been exposed for up to millions of years. However, their half-lives also render their concentrations insensitive to periods of burial and re-exposure of less than ca. 100 kyr; this can lead to problems with exposure dating due to nuclide inventories remaining from prior periods of exposure.

In situ cosmogenic ¹⁴C (in situ ¹⁴C) is also produced in quartz, but its 5.7 kyr half-life limits its utility for simple exposure dating because its concentration reaches secular equilibrium between production and decay after 25–30 kyr of continuous exposure. However, its rapid decay has also makes it sensitive to complex periods of burial and exposure since ca. 25–30 ka (e.g., Briner et al., 2014). In addition, its short half-life means measured concentrations are sensitive only to very rapid erosion rates (e.g., Gosse and Phillips, 2001; von Blanckenburg, 2005; Hippe et al., 2017, 2021), making many eroding landscape elements good targets for in situ ¹⁴C studies. In situ ¹⁴C is thus emerging as a powerful addition to the CN toolkit.

Several techniques for extracting in situ ¹⁴C from sand-sized quartz grains have been established (Lifton et al., 2001, 2015a; Goehring et al., 2019; Hippe et al., 2013; Lupker et al., 2019; Fülöp et al., 2019), but while coarse-grained quartz is common, it is not ubiquitous. Landscapes dominated by mafic or intermediate lithologies generally lack quartz, and fine-grained lithologies can limit the efficacy of quartz purification techniques; thus, applying in situ ¹⁴C to such rock types is currently problematic. However, the ability to extract and interpret in situ ¹⁴C concentrations reliably from quartz-poor and fine-grained lithologies would significantly broaden its applications to additional landscapes and enable pairing with additional nuclides such as ³⁶Cl. Indeed, early studies of in situ ¹⁴C in terrestrial rocks utilized whole-rock samples (e.g., Jull et al., 1992, 1994), until procedural difficulties shifted the focus to the simpler quartz production and extraction systematics (Lifton, 1997; Lifton et al., 2001).

As a first step in expanding the range of available sample targets, we have developed a software framework that estimates the production of in situ ¹⁴C from major elements found in typical rocks and potential mineral separates. We modified the MATLAB^® code from Lifton et al. (2014) to calculate compositionally dependent, site-specific production rates using nuclide-specific scaling, major-element oxide compositions, and measured and modeled nucleon excitation functions, referenced to geologically calibrated in situ ¹⁴C spallogenic production rates in quartz. Anticipating that appropriate extraction and CO₂ purification procedures can be developed, this new framework thus provides a critical first step for potential future applications incorporating quartz-poor or fine-grained samples.

2 Constraining compositionally dependent in situ ¹⁴C production rates

2.1 Geologic and experimental production rate calibrations

In situ CN applications require accurate estimates of the rate at which a given nuclide of interest is produced in the target mineral or rock. This is typically achieved by calibrating the production rate with CN measurements in samples from one or more sites with an independently well-constrained exposure history (e.g., Borchers et al., 2016; Phillips et al., 2016; Lifton et al., 2015b) or for radionuclides only with demonstrable surface stability, such that measured CN concentrations can be inferred to have reached a secular equilibrium between production and decay, at which point the concentration is only a function of time-integrated production rate and the decay constant (e.g., Jull et al., 1992; Borchers et al., 2016). Production rates can also be calibrated experimentally by exposing high-purity, low-background targets to the secondary cosmic-ray flux at given sites for a known duration under well-constrained conditions (e.g., Nishiizumi et al., 1996; Brown et al., 2000; Vermeesch et al., 2009).

Since production rates cannot be calibrated at every place on Earth, these site-specific estimates are typically scaled to other sites of interest using an appropriate scaling framework that accounts for spatial and temporal variations in the secondary cosmic-ray flux, arising from fluctuations in the geomagnetic field (parameterized by effective vertical cutoff rigidity, R_C, in GV), atmospheric depth (X, in g cm⁻²), and solar modulation (described by the parameter Φ in MV) (e.g., Lifton et al., 2014). Such scaling frameworks are typically referenced to conditions corresponding to sea level and high geomagnetic latitude (SLHL).

Geologic calibrations are generally preferable for minerals with specific compositions, since samples from sites with independently well-constrained exposure histories should incorporate natural geologic variability relevant over geologic time spans. Such calibrations for in situ ¹⁴C have focused on quartz to date, given its simple chemistry and weathering resistance, as noted above (e.g., Borchers et al., 2016; Phillips et al., 2016; Lifton et al., 2015b; Schimmelpfennig et al., 2012; Young et al., 2014), yet variable compositions require more complicated consideration of the compositional dependence of CN production (e.g., ³⁶Cl; Marrero et al., 2016a). It is often useful in such cases to utilize theoretical production rate estimates based on integrals of the differential cosmic-ray flux and the relationship between reaction probability and incident particle energy.

2.2 Theoretical production rate estimates

The probability that a given nuclear reaction will occur at a given kinetic energy, E, of an incident particle is described by the reaction cross-section (σ) in units of barns (1 barn = 10⁻²⁴ cm²). With the advent of accelerator mass spectrometry (AMS), cross-section measurements for reactions producing CNs have become relatively common, and knowledge of the variation of σ as a function of E for those reactions (known as an excitation function) are continuing to improve (e.g., Reedy, 2013). Proton-induced reactions are simpler to measure than those induced by neutrons because it is easier to accelerate protons into a mono-energetic beam. Mono-energetic (or quasi-mono-energetic) neutron reaction cross-sections are more difficult to obtain, however, and thus are often estimated from analogous proton cross-sections (Reedy, 2013).

Measured or modeled excitation functions can then be used to estimate theoretical production rates for a CN of interest using Eq. (1) below (e.g., Masarik and Beer, 2009):

$$\begin{array}{}\text{(1)}& \begin{array}{rl}{P}_j& \left(X,R_{\mathrm{C}},\mathrm{\Phi }\right)=\sum _i{\mathrm{ND}}_i\sum _k\underset{\mathrm{0}}{\overset{\mathrm{\infty }}{\int }}{\mathit{\sigma }}_{ijk}\left(E_k\right)J_k\\ & \left(E_k,X,R_{\mathrm{C}},\mathrm{\Phi }\right)\mathrm{d}{E}_k,\end{array}\end{array}$$

where ND_i is the target number density or number of atoms of the target element i per gram of sample material (at g⁻¹), σ_ijk (E_k) is the cross-section for the production of nuclide j (cm²) by particles of type k with energy E_k (MeV), and J_k ($E_k,X,R_{\mathrm{C}}$, Φ) is the differential flux of atmospheric cosmic-ray particles (cm⁻² yr⁻¹ MeV⁻¹) of type k with energy E_k at a location and time specified by X, R_C, and Φ.

The production of in situ ¹⁴C in silicates is dominantly from spallation of O, and theoretical simulations suggest minor spallogenic production from Mg, Al, and Si (Masarik and Reedy, 1995; Masarik, 2002). Production of in situ ¹⁴C from muons also occurs, either via slow negative-muon capture or by fast muon interactions (Heisinger et al., 2002a, b; Lupker et al., 2015; Balco, 2017). The muogenic component of in situ ¹⁴C production in surficial quartz at SLHL is significant, on the order of 20 % of total production (e.g., Lupker et al., 2015; Balco, 2017). However, muogenic production of in situ ¹⁴C has only been estimated experimentally from ¹⁶O (Heisinger et al., 2002a, b). Further work is needed in this area to better understand production from other muogenic reactions. We therefore focus on the dominant spallogenic pathways for the purposes of this initial study.

3 Methods

3.1 Software framework

Our MATLAB^®-based compositionally dependent in situ ¹⁴C production rate software framework builds on the LSDn nuclide-dependent scaling formulation of Lifton et al. (2014), which uses analytical approximations to Monte Carlo calculations of atmospheric differential flux spectra of neutrons, protons, and muons as functions of X, R_C, and Φ (Sato and Niita, 2006; Sato et al., 2008). We also incorporate the time-dependent gridded R_C (global grids of cutoff rigidity) and dipolar R_CD (geocentric dipolar cutoff rigidity) models of Lifton et al. (2016), based on the SHA.DIF.14k paleomagnetic model (Pavón-Carrasco et al., 2014). This work accounts for the effects of variable sample compositions on in situ ¹⁴C production by incorporating relevant reaction excitation functions and number densities for elements in the standard suite of major-element oxide compositions. Output from this new framework should complement current web-based cosmogenic-nuclide calculators incorporating the LSDn scaling framework and in situ ¹⁴C, including version 3 of the University of Washington's cosmogenic-nuclide calculators (herein UWv3: http://hess.ess.washington.edu/, last access: 1 November 2022) (Balco et al., 2008) and the Cosmic-Ray-prOduced NUclide Systematics on Earth (CRONUS-Earth) project calculator (CRONUSCalc; http://cronus.cosmogenicnuclides.rocks/, last access: 2 March 2022; Marrero et al., 2016b).

Reaction excitation functions for neutrons and protons were compiled from Reedy (2007, 2013) and the JENDL/HE-2007 database (Fukahori et al., 2002; Watanabe et al., 2011), found in the online Evaluated Nuclear Data File (ENDF, https://www-nds.iaea.org/exfor/endf.htm, last access: April 2020; Brown et al., 2018), for each of the major elements included in typical elemental oxide analyses. We consider empirical excitation functions to be generally more reliable than those derived from nuclear reaction models, and thus, we use empirical functions, if available. Five neutron and proton excitation functions are based on measurements by Reedy (2007, 2013) of elements at natural isotopic abundances (O, Mg, Al, Si, Fe), while we used modeled neutron and proton reaction excitation functions from JENDL/HE-2007 for the most abundant isotopes of the remaining elements considered (²³Na, ³¹P, ³⁹K, ⁴⁰Ca, ⁴⁸Ti, ⁵⁵Mn). Apart from the measured excitation function for in situ ¹⁴C production by neutron spallation from oxygen (Reedy, 2013), it is important to note that most of the Reedy (2007, 2013) neutron excitation functions are not directly measured but instead are derived from measured proton excitation functions. We utilized the JENDL/HE-2007 database because the relevant excitation functions extended to a maximum energy of 3 GeV, close to the maximum 10 GeV energy considered by Sato and Niita (2006) and Sato et al. (2008); a version of that nuclear data library was also utilized by those studies. The exceptions were the excitation functions for ³¹P, extending only to 0.2 GeV. Each excitation function was interpolated into logarithmic energy bins from 1 MeV to 200 GeV for both neutron (XX(n,x)¹⁴C) and proton (XX(p,x)¹⁴C) reactions, where XX is the target nuclide (Fig. 1). The cross-section at the highest measured or modeled energy reported for each excitation function is assumed to be constant beyond that energy up to 200 GeV, the maximum energy we consider.

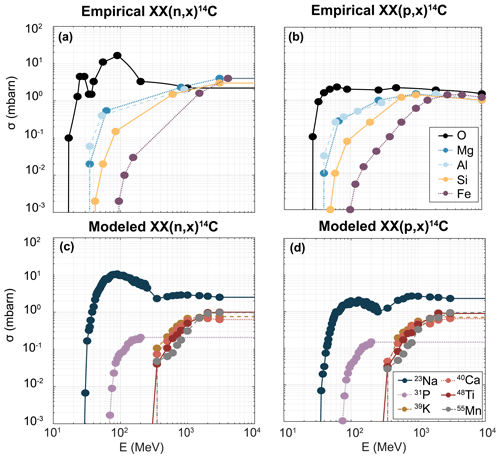
Figure 1 Empirical (Reedy, 2013) (panels a and b) and modeled (panels c and d) neutron and proton reaction excitation functions for in situ ¹⁴C production from various targets. The lines are linearly interpolated between points. Note that modeled predictions for ²³Na (JENDL/HE-2007; Fukahori et al., 2002; Watanabe et al., 2011) suggest the highest production of all targets considered.

We incorporate sample compositions using common major elemental oxide analyses (e.g., from X-ray fluorescence (XRF) measurements) to calculate ND for each element considered in Eq. (1). The ND value for each target element in a sample is then calculated per Eq. (2) for input to Eq. (1):

$$\begin{array}{}\text{(2)}& \mathrm{ND}={\displaystyle \frac{E_{\mathrm{Fr}}\cdot E_{\mathrm{Ox}}\cdot N_A}{\mathrm{100}\cdot A_{\mathrm{m}}}},\end{array}$$

where E_Fr is the elemental fraction in each oxide (formula mass of each element in its oxide divided by the total formula mass of the oxide (e.g., $\mathrm{Mg}/\mathrm{MgO}$ or $\mathrm{2}\mathrm{Al}/\mathrm{Al}$₂O₃)), E_Ox is the measured major elemental oxide weight percent input by the user, N_A is Avogadro's number (6.02214076×10²³ at mol⁻¹), and A_m is the molar mass of the element in g. This approach works for any silicate major elemental oxide composition input by the user.

3.2 Predicted compositionally dependent production rates

Theoretical compositionally dependent, site-specific in situ ¹⁴C production rates are reported relative to the SLHL in situ ¹⁴C global production rate in quartz, geologically calibrated as part of the CRONUS-Earth project (e.g., Borchers et al., 2016; Phillips et al., 2016) and supplemented with a subsequent production rate calibration dataset (Young et al., 2014) using the LSDn scaling framework (Lifton et al., 2014; Lifton, 2016) (Table S1 in the Supplement). All in situ ¹⁴C measurements in these studies were recalculated following Hippe and Lifton (2014). SLHL estimates are referenced to the year 2010 (Lifton et al., 2014; Lifton, 2016), assuming an atmospheric pressure of 1013.25 hPa (converted to atmospheric depth, g cm⁻²), an R_c value of 0 GV, a Φ₂₀₁₀ value of 624.5718 MV, and a fractional water content value, “w”, of 0.066 (Sato et al., 2006; Phillips et al. 2016). We recalibrated the in situ ¹⁴C spallogenic production rate at SLHL in quartz from the studies above by first calculating the unweighted mean and standard deviation of replicate analyses of samples at each site (to avoid biassing the results toward sites with more analyses). Best-fitting SLHL production rate estimates for each site were determined using a χ² minimization procedure. The unweighted mean and standard deviation of all sites were then calculated from the site-specific SLHL production rate estimates, yielding global SLHL values for quartz of 13.5±0.9 at g⁻¹ yr⁻¹ and 13.7±1.2 at g⁻¹ yr⁻¹ for the gridded R_C and geocentric dipolar R_CD records of Lifton (2016), respectively, as noted above. The latter is comparable to the calibrated value generated by the UWv3 calculator from the same dataset (Table S1). In the following discussion, we focus on the gridded R_C value (referenced below as P_Qcal), as it provides a somewhat better fit to the global calibration dataset. Corresponding geocentric dipolar values are included in Table S2.

For comparison, the purely theoretical in situ ¹⁴C production rate by nucleon spallation predicted at SLHL in quartz using Eq. (1) is 15.8 at g⁻¹ yr⁻¹ (P_Qref). This discrepancy with the calibrated value likely reflects uncertainties in both the excitation functions and the nucleon fluxes considered (Reedy, 2013; Sato and Niita, 2006; Sato et al., 2008). Giving more credence to the geologically calibrated quartz values, we account for this discrepancy similarly to Lifton et al. (2014), deriving a compositionally dependent, site-specific production rate (P_CD) by normalizing the predicted compositionally dependent production rate at the site of interest (P_CDpred) by the ratio of P_Qcal to P_Qref, as per Eq. (3). Another way to think of this is that the ratio of P_CDpred to P_Qref is the compositionally dependent scaling factor, multiplied by the geologically calibrated production rate in quartz, P_Qcal.

$$\begin{array}{}\text{(3)}& P_{\mathrm{CD}}=P_{\mathrm{Qcal}}{\displaystyle \frac{P_{\mathrm{CDpred}}}{P_{\mathrm{Qref}}}}\mathrm{at}{\mathrm{g}}^{-\mathrm{1}}{\mathrm{yr}}^{-\mathrm{1}}\end{array}$$

We compare P_CD values at SLHL to P_Qcal for compositions reflecting both individual minerals (Barthelmy, 2014; Morimoto, 1988) (i.e., mineral separates) and a broad range of silicate rock types (Parker, 1967; Fabryka-Martin, 1988) (i.e., whole-rock analyses) (Table 1). A pure calcite composition (CaCO₃) is assumed for limestone, and MgCa(CO₃)₂ is assumed for dolomite. Spallation production, in this case, is only possible from Ca and O, although we included the O number density contribution from CO₂ in the software framework. Thermal neutron production of in situ ¹⁴C from ¹²C or ¹³C is expected to be negligible and is not considered here (e.g., Wright et al., 2019).

Table 1 Elemental oxide compositions (weight %) for selected silicate minerals (Barthelmy, 2014; Morimoto, 1988) and rock types (Parker, 1967), used to calculate number densities (Eq. 2).

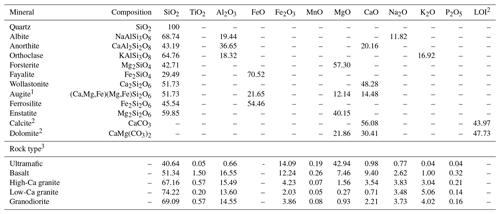
¹ Assumed empirical composition of augite (Morimoto, 1988; https://www.mindat.org/min-419.html, last access: 18 October 2022): (Ca_0.6Mg_0.2Fe_0.2)(Mg_0.5Fe_0.5)Si₂O₆. ² LOI: loss on ignition, used in oxygen number density calculation for carbonates; assumed to be entirely CO₂ in those cases. ³ Compositions from Parker (1967).

4 Results and discussion

4.1 Predicted modern production rates for silicate minerals and rock types

Predicted SLHL modern (i.e., 2010) spallogenic production rates for in situ ¹⁴C in the silicates considered here are generally lower than those from pure quartz (Fig. 2; Table 2), but spallation production from O dominates throughout the compositional range we explored (Table 3). As expected from reaction systematics, ¹⁴C production rates tend to decline rapidly with progressively increasing atomic mass of the target nuclide (Fig. 2). Interestingly, the production rate predicted for albite using the excitation functions from JENDL/HE-2007 for spallation reactions on ²³Na is comparable to that of quartz. We note that the JENDL/HE-2007 model ²³Na(n,x)¹⁴C excitation function exhibits a broad peak between ca. 30–350 MeV, with cross-sections comparable to that of the empirical O(n,x)¹⁴C excitation function of Reedy (2013) (Fig. 1), suggesting similar production magnitudes for the two reactions. To our knowledge, no comparable empirical excitation functions for the ²³Na(n,x)¹⁴C or ²³Na(p,x)¹⁴C reactions have been published to date, making the model reactions difficult to validate. Predicted production rates for Mg-rich silicates such as forsterite and enstatite are ca. 7 %–10 % lower than in quartz, while Al-rich minerals such as Ca- and K-feldspars yield production rates 12 %–13 % below quartz. Ca-rich wollastonite exhibits less than 1 % of its total ¹⁴C production from Ca, yielding a production rate more than 20 % below that of quartz, while Fe-rich minerals such as ferrosilite and fayalite suggest SLHL production rates ca. 32 % and 41 % less than quartz, respectively. Predicted production rates for two carbonate minerals considered, calcite and dolomite, are 12 % and 3 % less than quartz, respectively.

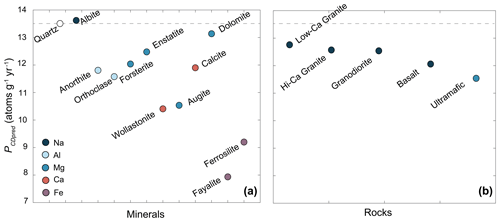
Figure 2 Predicted theoretical SLHL production of in situ ¹⁴C (P_CDpred) in minerals (a) and rocks (b) relative to that in pure quartz (dashed gray line). The color of each symbol reflects the element that contributes the highest proportion of production after oxygen and silica.

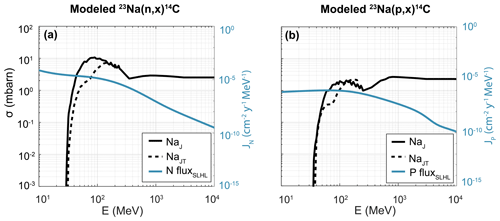
Figure 3 Modeled neutron (a) and proton (b) cross-sections for ²³Na from JENDL/HE-2007 (Na_J, solid line) compared to the spliced TENDL-2019 at energies ≤0.2 GeV and JENDL/HE-2007 > 0.2 GeV (²³Na_TJ, dashed line). Differential neutron and proton fluxes at SLHL (J_N and J_P, respectively) (Sato et al., 2008) are plotted in their respective panes to illustrate the combined effect of excitation function and flux on in situ ¹⁴C production.

The P_CD values for selected rock types (ultramafic, basalt, high-Ca granite, low-Ca granite, and granodiorite; Fabryka-Martin, 1988) follow a similar pattern to the individual minerals, with total production rates less than that of quartz but with less overall variation (Fig. 2; Table 2). Predicted whole-rock production rates tend to increase with decreasing Fe and Mg content, with P_CD values ranging from nearly 15 % less than quartz for ultramafic compositions to ca. 5 %–7 % below that of quartz for more felsic compositions. As with the idealized mineral compositions, spallation from O dominates in situ ¹⁴C production (>90 % for all compositions considered), with lesser production from Si, Al, Na, and Mg. Only minor production contributions from Ca and Fe are predicted (typically <1 %).

Table 2 Predicted modern in situ ¹⁴C spallogenic production rates (at g⁻¹ yr⁻¹) at SLHL from neutrons and protons in minerals and rock types considered, both theoretical (P_CDpred) and normalized to calibrated production in quartz (P_CD) using the gridded R_C record of Lifton (2016).

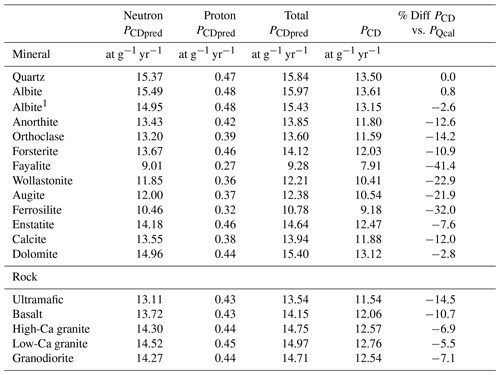
¹ Production is calculated using the spliced TENDL-2019 and JENDL/HE-2007 proton and neutron excitation functions. (Na_TJ in text). All other Na production rates use JENDL/HE-2007 exclusively.

4.2 Assessing uncertainty in predicted compositionally dependent production rates

There are three main sources of uncertainty in our predicted production rates, associated with the particle spectra, the geologic production rate calibration for in situ ¹⁴C in quartz, and the excitation functions. We note that these are not entirely independent, as the LSDn-based production rate calibration utilizes both the particle spectra of Sato et al. (2008) and the excitation functions of Reedy (2013). Sato et al. (2008) quote statistical uncertainties in their modeled particle fluxes on the order of 5 %–20 % between ca. 10 km altitudes and sea level, respectively, although Lifton et al. (2014) note that predictions within this altitude range show good agreement with measured differential fluxes and no evidence of systematic errors. The conservative uncertainty in the recalibrated in situ ¹⁴C global production rate in quartz is on the order of 6 %–7 % using the gridded R_C geomagnetic framework and LSDn scaling. Reedy (2013) suggests uncertainties on the order of 10 % for the empirical excitation functions presented. However, Reedy (2013) also suggests that modeled cross-sections may differ from empirical ones for a given nuclide by a factor of ≈2. Thus, assessing the uncertainty in the modeled functions of JENDL/HE-2007 is more difficult.

We attempted to assess this latter uncertainty by comparing results using JENDL/HE-2007 to predictions incorporating the more recent TENDL-2019 database (Koning et al., 2019). We focused on the proton and neutron excitation functions for ¹⁴C production from ²³Na, since our predictions using the JENDL/HE-2007 ²³Na excitation functions suggest comparable production to that from O (Fig. 1; Table 2). However, TENDL-2019 excitation functions only extend to an energy of 200 MeV, although at a higher resolution than JENDL/HE-2007. We thus compared albite production rates predicted using the JENDL/HE-2007 excitation function alone (Na_J) with those incorporating spliced neutron and proton excitation functions using TENDL-2019 for E≤200 MeV and JENDL/HE-2007 for E>200 MeV (Na_TJ) (Fig. 3).

Neutron and proton excitation functions for ²³Na have similar thresholds of ca. 30–35 MeV in both JENDL/HE-2007 and TENDL-2019 (Fig. 3). Of note, the low-energy peaks in the TENDL-2019 excitation functions are narrower, ca. 30 % lower, and occur at a slightly higher energy than those of JENDL/HE-2007 (ca. 150 MeV vs. ca. 90 MeV, respectively). However, the predicted production rate for albite using the spliced Na_TJ excitation functions is only ca. 3 % less than that using the Na_J excitation functions alone (Table 2), which is also reflected in the lower production proportion from Na of ca. 5 % in the spliced version vs. ca. 9 % in the Na_J version (Table 3).

Table 3 Percentage of total theoretical predicted modern SLHL in situ ¹⁴C production (P_CDpred) by element for each mineral and rock type considered.

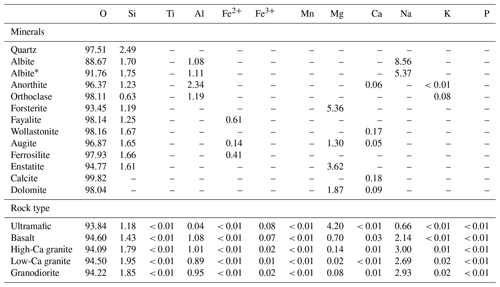
^∗ Production is calculated using the spliced TENDL-2019 and JENDL/HE-2007 proton and neutron excitation functions (Na_TJ in text). All other Na production rates use JENDL/HE-2007 exclusively.

Apart from the modeled ²³Na excitation functions, the remaining modeled excitation functions have only a minor impact on the overall production rates we predict. The percentages of total production of in situ ¹⁴C from ⁵⁵Mn, ⁴⁸Ti, ⁴⁰Ca, ³⁹K, and ³¹P range from <0.001 % to 0.2 % for the compositions considered (Table 3). Even if the modeled reaction cross sections are off by a factor of 2, as suggested by Reedy (2013), the impact to overall production is small. For instance, doubling the percentage of ¹⁴C production from Ca for wollastonite would only increase predicted production to 0.4 %. In addition, we argue that calculating production using modeled excitation functions for only the most abundant isotope of each of these elements, instead of excitation functions reflecting their natural isotopic abundances, introduces negligible additional uncertainty. For example, we assume 100 % of production of in situ ¹⁴C from ⁴⁸Ti, even though ⁴⁸Ti comprises only 73 % of Ti isotopes. However, ⁴⁸Ti contributes <0.001 % of total production for the compositions we considered; it is unlikely that including excitation functions for other common Ti isotopes would change that prediction significantly. Similar arguments can be made for the other isotopes referenced above. We therefore argue that the overall additional uncertainty in our predictions that might be introduced by using more conservative estimates of potential errors in the modeled reaction cross-sections would be insignificant relative to other uncertainties in the calculations for the compositions considered. That said, future additional empirical excitation functions for neutron and proton reactions using these elements in their natural abundances would likely improve our predictions.

Based on these results, we suggest assuming a 10 % uncertainty for the JENDL/HE-2007 excitation functions overall, pending empirical validation. Thus, considering the three sources of uncertainty above, we suggest that a reasonable estimate of current uncertainty on our theoretical production rates might be on the order of 10 %–15 %, also pending validation with geologic calibrations, assuming extraction and CO₂ purification hurdles can ultimately be overcome.

4.3 Comparisons with previous studies

We compare output of our software framework to two earlier studies that also calculated theoretical in situ ¹⁴C production rates from targets of varying composition (Fabryka-Martin, 1988; Masarik, 2002), without adjusting our predictions to the geologically calibrated production rate in quartz. First, Fabryka-Martin (1988) estimated SLHL secular-equilibrium in situ ¹⁴C concentrations at depths of ∼20 cm for ultramafic rock, basalt, high-Ca granite, low-Ca granite, and limestone compositions, following Parker (1967) (Table 4). The equilibrium concentrations were calculated assuming neutron spallation production only from oxygen and a SLHL production rate of 26 at g⁻¹ yr⁻¹ from oxygen (Yokoyama et al., 1977) based on excitation functions from Reedy and Arnold (1972). We derived secular equilibrium SLHL production rates from Fabryka-Martin (1988) by multiplying the concentrations by the ¹⁴C decay constant of $\mathrm{1.216}\times {\mathrm{10}}^{-\mathrm{4}}$ yr⁻¹ (Table 4, P_O−FM). Considering only theoretical production from O in our results (Total P_CDpred in Table 2 multiplied by the corresponding O production proportion in Table 3), our P_O values in Table 4 are ca. 40 %–45 % below those derived from Fabryka-Martin (1988). However, it should be pointed out that Yokoyama et al. (1977) suggest ±35 % uncertainty (1σ) in their in situ ¹⁴C production rate estimate used by Fabryka-Martin (1988), so our theoretical P_O values using more accurate particle fluxes and excitation functions lie well within that range.

Table 4 Predicted modern in situ ¹⁴C production rates at SLHL for neutron spallation from O derived from secular equilibrium concentrations (N_SE) at ca. 20 cm depth for different rock types (Fabryka-Martin, 1988) compared to our software framework. Note that these estimates are not normalized relative to P_Qcal for straightforward comparison to Fabryka-Martin's (1988) predictions.

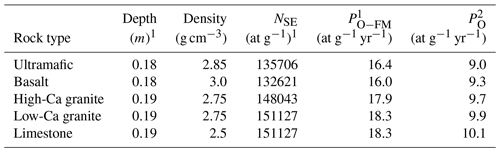
¹ Data from Fabryka-Martin (1988), assumes SLHL production rate from oxygen in Yokoyama et al. (1977). ² Data from this study, assuming only production from neutron spallation of O and an attenuation length of 160 g cm⁻².

The second study we considered (Masarik, 2002) is a conference abstract that presents formulas for estimating compositional dependence of in situ cosmogenic-nuclide SLHL production rates by neutron spallation, including ¹⁴C, derived from numerical simulations. For in situ ¹⁴C production, Masarik (2002) considers the target elements O, Mg, Al, Si, and Fe, parameterized in terms of the weight fractions of each (Table 5). Total production rates from Masarik (2002) (P_M02) in Table 5 are typically ca. 10 %–20 % higher than neutron-only theoretical production rates for rock and mineral compositions considered in this study (Neutron P_CDpred, Table 2). Being an abstract, details underlying the simulations and calculations in Masarik (2002) are sparse, but we suggest a combination of differences in the differential neutron flux spectra (Masarik and Beer, 1999, vs. Sato et al., 2008) and excitation functions (e.g., Reedy and Masarik, 1995, vs. Reedy, 2013) used in the two studies, as well as unstated uncertainties in the Masarik (2002) coefficients, may be the sources of the discrepancies in the predictions of the respective studies.

Table 5 Neutron-only SLHL in situ ¹⁴C production based on Masarik's (2002; P_M02) theoretical predictions for compositions considered in this work, compared to modern SLHL neutron-only production predicted here (also see Table 2). Note that these estimates are not normalized relative to P_Qcal to enable direct comparison to Masarik's (2002) predictions.

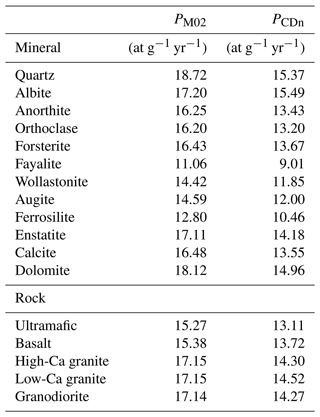
We derived a similar elemental parameterization to that of Masarik (2002) for SLHL in situ ¹⁴C production in atoms g-element⁻¹ yr⁻¹. We include production from both neutrons and protons for each element we consider, given by

$$\begin{array}{}\text{(4)}& \begin{array}{rl}{P}_{\mathrm{CDpred}}& =\mathrm{29.01}\left[\mathrm{O}\right]+\mathrm{15.59}\left[\mathrm{Na}\right]+\mathrm{2.19}\left[\mathrm{Mg}\right]\\ & +\mathrm{1.67}\left[\mathrm{Al}\right]+\mathrm{0.84}\left[\mathrm{Si}\right]+\mathrm{0.22}\left[\mathrm{P}\right]+\mathrm{0.10}\left[\mathrm{Fe}\right]\\ & +\mathrm{0.08}\left[\mathrm{K}\right]+\mathrm{0.06}\left[\mathrm{Ca}\right]+\mathrm{0.05}\left[\mathrm{Ti}\right]+\mathrm{0.03}\left[\mathrm{Mn}\right],\end{array}\end{array}$$

where the bracketed values are the respective elemental fractions derived from the measured major elemental analysis. In situ ¹⁴C production rates predicted using this equation for the compositions considered in Table 1 are identical to the P_CDpred values in Table 2, since both are derived using the same software framework.

In addition to the theoretical studies, Handwerger et al. (1999) measured in situ ¹⁴C concentrations in carbonate deposits (limestone bedrock and tufa) from well-preserved Provo-level shoreline features associated with Pleistocene Lake Bonneville, Utah, to calibrate in situ ¹⁴C spallogenic production rates in calcite. The late Pleistocene lake-level history of Lake Bonneville is well constrained by traditional radiocarbon dates and has been used for geological calibration of a number of cosmogenic nuclides (Lifton et al., 2015b). In situ ¹⁴C measurements in Handwerger et al. (1999) were reduced according to standard methods for radiocarbon in organic materials, but Hippe and Lifton (2014) subsequently developed comprehensive data reduction procedures specifically for in situ ¹⁴C. Unfortunately, Handwerger et al. (1999) do not present full details of their analytical results and calculations – we thus cannot correct their data to current standards using the Hippe and Lifton (2014) protocols. If we assume such corrections would be small relative to the resulting in situ ¹⁴C concentrations in their calibration samples, neglecting three anomalous results and using the age of the initial Provo shoreline formation from Lifton et al. (2015a) of 18.3±0.3 cal ka, their mean in situ ¹⁴C concentration is ($\mathrm{3.75}\pm \mathrm{0.26})\times {\mathrm{10}}^{\mathrm{5}}$ at g⁻¹ CaCO₃. This corresponds to a local production rate of ca. 51 at g⁻¹ yr⁻¹. In contrast, the theoretical local production rate calculated with our software framework is ca. 43.9 at g⁻¹ yr⁻¹, ∼15 % lower than the derived local production rate. In addition, the predicted value normalized to P_Qcal yields 37.5 at g⁻¹ yr⁻¹, 27 % lower than Handwerger et al. (1999). Given the uncertainties in the uncorrected Handwerger et al. (1999) dataset and the suggested uncertainties in our method, we find reasonable agreement between our production rate estimates and those of Handwerger et al. (1999).

5 Conclusions

As a first step in exploring potential applications of in situ ¹⁴C to quartz-poor or fine-grained rock types, we have extended the functionality of the MATLAB^®-based LSDn nuclide-specific scaling framework (Lifton et al., 2014; Lifton, 2016) to estimate spallogenic production of in situ ¹⁴C in rock and mineral compositions other than pure quartz at sites of interest. We account for compositionally dependent production by using measured and modeled nucleon excitation functions for target elements in major element oxide analyses (e.g., XRF), in concert with secondary cosmic-ray differential fluxes, as per Lifton et al. (2014). The ratio of resulting theoretical compositionally dependent in situ ¹⁴C production rates to the corresponding theoretical quartz production rate is then multiplied by the geologically calibrated production rate in quartz, placing the theoretical production rates in a calibrated context. Exploring a broad range of mineral and rock compositions indicates that production is dominated by oxygen spallation, as expected (>90 % at SLHL), but with a general decrease in total production rate with more mafic (particularly Fe-rich) compositions. Although this study confirms previous work identifying Si, Mg, and Al as important targets, we also find, for the first time, that Na appears to contribute significantly. Future nucleon excitation function measurements, particularly for Na reactions, should improve the robustness of this software tool further. This framework is thus an important initial step forward in applying in situ ¹⁴C to a broader array of landscapes.