the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Cosmogenic 10Be in pyroxene: laboratory progress, production rate systematics, and application of the 10Be–3He nuclide pair in the Antarctic Dry Valleys
Allie Balter-Kennedy
Joerg M. Schaefer
Roseanne Schwartz
Jennifer L. Lamp
Laura Penrose
Jennifer Middleton
Jean Hanley
Bouchaïb Tibari
Pierre-Henri Blard
Gisela Winckler
Alan J. Hidy
Greg Balco
Here, we present cosmogenic-10Be and cosmogenic-3He data from Ferrar dolerite pyroxenes in surficial rock samples and a bedrock core from the McMurdo Dry Valleys, Antarctica, with the goal of refining the laboratory methods for extracting beryllium from pyroxene, further estimating the 10Be production rate in pyroxene and demonstrating the applicability of 10Be–3He in mafic rock. The ability to routinely measure cosmogenic 10Be in pyroxene will open new opportunities for quantifying exposure durations and Earth surface processes in mafic rocks. We describe scalable laboratory methods for isolating beryllium from pyroxene, which include a simple hydrofluoric acid leaching procedure for removing meteoric 10Be and the addition of a pH 8 precipitation step to reduce the cation load prior to ion exchange chromatography. 10Be measurements in pyroxene from the surface samples have apparent 3He exposure ages of 1–6 Myr. We estimate a spallation production rate for 10Be in pyroxene, referenced to 3He, of 3.6 ± 0.2 atoms g−1 yr−1. 10Be and 3He measurements in the bedrock core yield initial estimates for parameters associated with 10Be and 3He production by negative-muon capture ( and ).
Next, we demonstrate that the 10Be–3He pair in pyroxene can be used to simultaneously resolve erosion rates and exposure ages, finding that the measured cosmogenic-nuclide concentrations in our surface samples are best explained by 2–8 Myr of exposure at erosion rates of 0–35 cm Myr−1. Finally, given the low 10Be in our laboratory blanks (average of 5.7 × 103 atoms), the reported measurement precision, and our estimated production rate, it should be possible to measure 2 g samples with 10Be concentrations of 6 × 104 and 1.5 × 104 atoms g−1 with 5 % and 15 % uncertainty, respectively. With this level of precision, Last Glacial Maximum to Late Holocene surfaces can now be dated with 10Be in pyroxene. Application of 10Be in pyroxene, alone or in combination with 3He, will expand possibilities for investigating glacial histories and landscape change in mafic rock.
- Article
(3066 KB) - Full-text XML
-
Supplement
(794 KB) - BibTeX
- EndNote
Cosmogenic nuclides are formed in minerals when rock is exposed to secondary cosmic radiation, and their concentrations at and near the Earth's surface hold information about exposure durations, burial time, and erosion rates (e.g., Cerling, 1994; Kurz and Brook, 1994; Lal, 1991; Nishiizumi et al., 1991; Schaefer et al., 2022). Most simply, the concentration of cosmogenic nuclides in rock serves as an exposure clock because they accumulate at known rates. It is also possible to deconvolve complex exposure histories, involving exposure, burial, and rock erosion, by combining measurements of multiple cosmogenic nuclides with different half-lives (e.g., Balco and Rovey, 2010; Granger, 2006; Lal, 1991; Nishiizumi et al., 1991; Schaefer et al., 2016a). In quartz-bearing (felsic) rocks, 21Ne (stable), 10Be ( Myr), 26Al ( Myr), and 14C ( kyr) are routinely measured, and different combinations of these nuclides can be used to quantify geomorphic processes on 103–106-year timescales (e.g., Balco and Shuster, 2009; Hippe, 2017; Young et al., 2021). 10Be in quartz is the most commonly used nuclide–mineral pair because this mineral phase is abundant at the Earth's surface, the production pathways for 10Be in quartz are well understood, and advances in beryllium extraction procedures and mass spectrometry have yielded measurement precision as low as ∼2 %.
Fewer cosmogenic nuclides are routinely measured in lithologies where quartz is absent. The stable nuclide 3He is the most widely used in mafic rocks because it is easily measured in several mineral phases, including pyroxene and olivine (Blard et al., 2021; Kurz, 1986). The radionuclide 36Cl ( Myr) is also routinely measured in feldspar or whole rock, so the 36Cl–3He pair could in principle be used to detect burial up to ∼1.5 Ma. Prior work demonstrates that measuring 10Be in pyroxene and olivine is possible (Blard et al., 2008; Eaves et al., 2018; Ivy-Ochs et al., 1998; Nishiizumi et al., 1990), which would extend the useful range for multi-nuclide studies in mafic rocks to >5 Ma, ideal for Miocene to Pleistocene timescales.
Several studies report 10Be concentrations in pyroxene (Blard et al., 2008; Eaves et al., 2018; Ivy-Ochs et al., 1998) but highlight challenges to measuring 10Be in this mineral phase. First, the mineral composition of pyroxene (XYSi2O6, where X and Y are both divalent cations (primarily Ca, Fe, or Mg), or X is a monovalent cation (Na, Li), and Y is a trivalent cation (Al, Fe); Nespolo, 2020)) is highly variable. In contrast to quartz (SiO2), the high cation quantities in pyroxenes present a significant challenge for isolating beryllium using ion exchange chromatography, limiting the feasible sample size. Second, early work on pyroxenes demonstrated difficulty in removing meteoric 10Be, atmospherically produced 10Be scavenged by precipitation. In quartz, meteoric 10Be is typically removed by repeated leaching in hydrofluoric acid (HF; Brown et al., 1991; Kohl and Nishiizumi, 1992). Ivy-Ochs et al. (1998) demonstrated that 10Be concentrations in pyroxenes with exposure ages of ∼106 years did not stabilize after several rounds of HF leaching, suggesting that meteoric 10Be was present in clays and other weathering products built up within the pyroxene lattice. In samples with 104-year exposure ages, Blard et al. (2008) successfully decontaminated pyroxene of meteoric 10Be by implementing a powdering step to increase the surface area of pyroxene grains prior to leaching the samples in hydroxylammonium chloride, which removes iron oxides and releases meteoric 10Be from the pyroxene grains. This result was replicated by Eaves et al. (2018), but this procedure has yet to be tested on pyroxenes with exposure durations longer than 104 years, in which weathering products have had more time to accumulate within the pyroxene lattice.
For cosmic-ray-produced nuclides to be useful in geologic applications, the production rate of these nuclides at the Earth's surface and with depth in rock must be known. 10Be and 3He, like most cosmogenic nuclides, are produced by spallation, fast-muon interactions, and negative-muon capture, production pathways that display different dependencies (Dunai, 2010). Spallation reactions, induced by high-energy (30 MeV–1 GeV) neutrons, comprise the majority of production at the Earth's surface but decrease rapidly with depth due to strong interaction with matter, with a latitude-dependent attenuation length in rock of 140–160 g cm−2 (Gosse and Phillips, 2001). Production by muons, which interact weakly with matter, comprise up to ∼2 % of production at the surface but surpass spallation production below the upper several meters of rock. For this weak interaction production pathway, 10Be and 3He are primarily produced by negative-muon capture in the upper rock column, while fast-muon reactions attenuate more slowly with depth from the surface (Balco, 2017; Heisinger et al., 2002a, b; Lal, 1987; Larsen et al., 2021; Nesterenok and Yakubovich, 2016).
The spallation production rate of 3He in pyroxene is well known (Borchers et al., 2016; Goehring et al., 2010). Eaves et al. (2018) used cross-calibration between 10Be and 3He (combining new data with those of Blard et al., 2008, and Nishiizumi, 1990) to estimate a spallation 10Be production rate in pyroxene of 3.6 ± 0.8 atoms g−1 yr−1 (Eaves et al., 2018, also calibrated a production rate for 10Be in pyroxene of 3.2 ± 0.8 atoms g−1 yr−1 using independent age data). Theoretical studies predict that cosmogenic 3He is produced by muon interactions (Lal, 1987; Nesterenok and Yakubovich, 2016), and recent 3He measurements in a 300 m drill core from the Columbia River Basalt provide unambiguous empirical evidence for muon production of 3He at a total production rate of 0.23–0.45 atoms g−1 yr−1 at the Earth's surface at sea level high-latitude (Larsen et al., 2021). Although parameters associated with muon production of 10Be in quartz are well known (Balco, 2017), muon production of 10Be in pyroxene is not yet quantified.
Here, we describe progress in laboratory techniques for extracting beryllium from pyroxene, building upon the previous work of Blard et al. (2008) and Eaves et al. (2018). We then use our new 10Be and 3He measurements in pyroxenes from surface samples and a 1.7 m drill core from the McMurdo Dry Valleys, Antarctica, to further calibrate the production rate of 10Be by spallation and present initial constraints on 10Be and 3He production by negative-muon capture. Finally, we use the sample set from the McMurdo Dry Valleys to demonstrate use of the 10Be–3He pair for simultaneously estimating exposure ages and erosion rates in mafic rock.
The McMurdo Dry Valleys region of Antarctica is a 4800 km2 area in the northern Transantarctic Mountains, bounded by the McMurdo Sound to the west and the East Antarctic Ice Sheet (EAIS) to the east. Local basement rock and overlying sedimentary rocks are intruded by Jurassic Ferrar dolerite sills (∼180 Ma; Burgess et al., 2015; McKelvey and Webb, 1962). The landscape is dissected by the large, east–west trending Taylor, Wright, and Victoria Valley systems that formerly held outlet glaciers draining the EAIS to the Ross Sea and are flanked by mountains, including the Asgard and Olympus ranges (Fig. 1). Geomorphic evidence suggests that this landscape had formed by the mid-Miocene and has since been preserved in a cold, hyperarid climate (e.g., Sugden et al., 1995). This hypothesis is supported by extremely high cosmogenic-nuclide concentrations throughout the region that are consistent with some of the lowest subaerial erosion rates on Earth (0–30 cm Myr−1; Bruno et al., 1997; Ivy-Ochs et al., 1995; Margerison et al., 2005; Schäfer et al., 1999; Summerfield et al., 1999).
Large meltwater features, including channels, potholes, plunge pools, corrugated bedrock, and megaripples, found throughout the region are thought to have been carved by mid-Miocene outburst floods originating beneath an expanded, wet-based EAIS (Denton and Sugden, 2005). 40Ar 39Ar ages of in situ volcanic ashes embedded in associated sediments provide limiting ages of these features, suggesting that the major topographic features of the Dry Valleys formed by ∼15 Ma and that the last glacial overriding event likely occurred by 14 Ma and possibly by 14.8 Ma (Denton et al., 1993). One prominent meltwater feature is the Labyrinth, a channel-and-pothole system carved into Ferrar dolerite bedrock located at the foot of Wright Upper Glacier, an outlet glacier of the EAIS. 39Ar 40Ar ages of ashes from erosional surfaces within the Labyrinth date the last incision of this feature to ∼14.5 Ma (Lewis et al., 2006). In contrast, cosmogenic-nuclide concentrations in similar sandstone channel systems in Sessrumnir Valley, Asgard Range, near, although not directly adjacent to, the Labyrinth suggest that the Dry Valleys landscape has been more dynamic since the mid-Miocene. There, paired 10Be–21Ne data reveal lower-than-expected cosmogenic-nuclide concentrations, which can be explained if these features had formed by wind erosion since ∼14 Ma at erosion rates of ∼60–150 cm Myr−1 or were incised by subglacial flooding during a later episode of ice cover, such as during the Pliocene (Middleton et al., 2012). Overall, channel and pothole features throughout the Dry Valleys, including the Labyrinth, may have experienced ∼14–15 Myr of exposure, although the mechanism and timing of formation for many of these features remain up for debate.
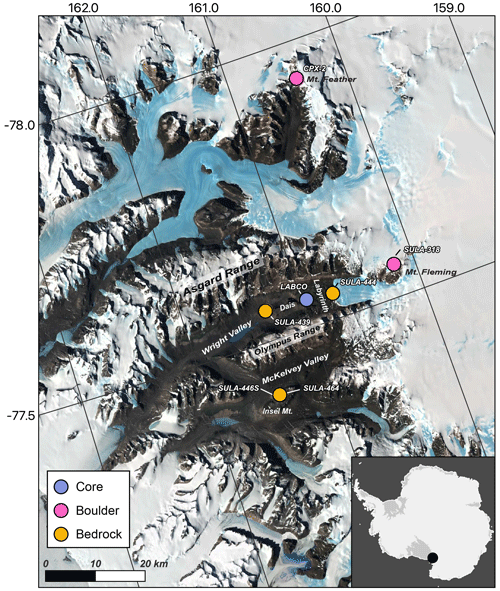
Figure 1Map showing sample locations and places discussed in the text generated using Quantarctica Version 3 (Matsuoka et al., 2021). The base map employs the LIMA Landsat high-resolution virtual mosaic (Bindschadler et al., 2008).
In this study, we focus on Ferrar dolerite samples collected throughout the Dry Valleys region, originally measured for cosmogenic noble gasses by Bruno et al. (1997) and Schaefer et al. (1999), that can be grouped into two geomorphic environments: (1) boulders that are erosional remnants of the Sirius Group, located atop Mt. Fleming and Mt. Feather at elevations >2000 m in the Stable Upland Zone, which features the coldest and driest conditions in the Dry Valleys (Lamp et al., 2017, and references therein), and (2) bedrock collected between ∼850–1400 m from deeply weathered platforms at Mt. Insel, the Dais, and the Labyrinth in the inner Dry Valleys, somewhat closer to the Ross Sea, where conditions are slightly warmer and wetter (see Schäfer et al., 1999, and Bruno et al., 1997, for further details; Fig. 1). In addition to surface samples, we include results from a bedrock core collected from an erosional surface of the Labyrinth.
Table 1Location information for surface samples.

a Sample is listed as Flem94-18 in Bruno et al. (1997) and is the only sample listed here included in that publication. b Sample NXP 93*52 is derived from the same sample as the reference material CRONUS-P (Schaefer et al., 2016b). c Latitudes and longitudes for surface samples are approximated from the United States Geological Survey (1988) Taylor Glacier map, as latitudes and longitudes were not reported in the original publications associated with these samples (Bruno et al., 1997; Schäfer et al., 1999). See Supplement for location approximation methods. d Sample elevations used here are 120 m lower than reported in Schäfer et al. (1999) due to inaccuracies with pressure-based altimeter/early handheld GPS. See Supplement.
3.1 Field methods
We present results from surficial rock samples and a bedrock core. The surficial rock samples are six Ferrar dolerites collected from the upper few centimeters of rock in the Dry Valleys in the early to mid-1990s and described by Schäfer et al. (1999) and Bruno et al. (1997) (two boulders and four bedrock surfaces; Table 1). We redetermined surface sample locations and elevations with reference to the US Geological Survey Taylor Glacier topographic map (1988) because of some inaccuracies with the location information in those original publications (see Table S1 in the Supplement). The Labyrinth bedrock core was collected by a group led by John Stone of the University of Washington in austral summer 2009 as part of the CRONUS-Earth project (Table 1, Fig. 1, Sect. 2). The rock type is fine- to medium-grained Ferrar dolerite, with roughly equal parts of pyroxene and plagioclase. The coring site was chosen because erosion rates appeared to be low (10–20 cm Myr−1), and previous work suggests that the site has been exposed for the last ∼14 Myr (Lewis et al., 2006; Sect. 2). Importantly, below 18 cm depth, there was a discrepancy between the drillers' measurements of the core barrel and the recovered core length by 1–4 cm. No material was lost between 18–167 cm, but we account for this discrepancy by adjusting the absolute sample depths below 18 cm in a model fitting exercise described in Sect. 5.1.1. The core was split into sections at the University of Washington and measured for rock density. Four rock density measurements from 0.5–1.5 m depth in the core gave consistent values from 2.93 ± 0.02 to 2.96 ± 0.02 g cm−3, averaging 2.94 ± 0.03 g cm−3. Sections of the core were then sent to several institutions, including Lamont–Doherty Earth Observatory (LDEO), Berkeley Geochronology Center (BGC), and Le Centre de Recherches Pétrographiques et Géochimiques (CRPG), for cosmogenic-nuclide analysis.
3.2 Cosmogenic-nuclide measurements
3.2.1 Mineral separation and decontamination
Pyroxene separated from the surface samples was prepared at LDEO, and samples from the Labyrinth core were prepared at LDEO, BGC, and CRPG. At LDEO, samples were crushed and sieved to a grain size at which we observed mostly mono-mineralic grains (for the fine- to medium-grained samples here, we used the 32–125 µm fraction) and then leached at room temperature in 10 % H3PO4 overnight to remove iron oxides. Then light minerals (mostly plagioclase) were removed using sodium polytungstate with a density of 3.0 g cm−3. Next, samples were passed through a magnetic separator, and a hand magnet was used to remove magnetic minerals. To decontaminate the pyroxene grains of meteoric 10Be, samples were leached in a 1 %HF 1 %HNO3 solution and placed on a table shaker at room temperature for 5–6 h twice, then a third time overnight, rinsing samples thoroughly between each round of leaching (Bromley et al., 2014; Kohl and Nishiizumi, 1992). Overall, we targeted ∼30 % sample mass loss after leaching. To confirm sufficient removal of meteoric 10Be, five leaching rounds were performed on sample 444, and the 10Be concentration was measured on a split taken after each round. After two rounds of leaching, with ∼25 % sample loss, 10Be concentrations in sample 444 remain consistent within measurement error, suggesting that this leaching method was sufficient for removing meteoric 10Be (Fig. 2). Pyroxenes separated at LDEO are referred to as “LDEO-prepared.”
Table 2Cosmogenic-nuclide concentrations, apparent exposure ages, and apparent erosion rates for surface samples.

a Sample is listed as Flem94-18 in Bruno et al. (1997) and is the only sample listed here that is included in that publication. b Sample NXP 93*52 is derived from the same sample as the reference material CRONUS-P (Schaefer et al., 2016b). c 3He concentrations listed here are for the only surface sample in which 10Be was not measured. See Table 3 for subsurface sample results. To calculate the 10Be surface exposure age, a surface 10Be concentration was approximated by fitting an exponential curve to the subsurface 10Be data. d 3He concentrations reported for all samples except the Labyrinth core were measured at LDEO and were originally reported in Schaefer et al. (2006). e Apparent 10Be exposure ages calculated using the 10Be in pyroxene spallation production rate from Eaves et al. (2018) of 3.6 ± 0.8 atoms g−1 yr−1 and v3 of the online exposure age calculator.

Figure 210Be concentrations measured after each of the five progressive leaches on pyroxenes from sample 444. Total sample material loss ranges from 9 % in Leach 1 to 60 % in Leach 5. The dashed black line shows the average 10Be concentration of HF2–HF5, and the shaded box shows the standard deviation of those 10Be concentrations. The HF2–HF5 concentrations overlap within uncertainty, suggesting that 20 %–25 % sample loss is enough to sufficiently remove meteoric 10Be from old Ferrar dolerite samples.
Pyroxene preparation procedures at BGC and CRPG, where pyroxenes were measured only for 3He, were similar to those at LDEO but did not include an HF leaching step. BGC received from the University of Washington a heavy mineral concentrate prepared by crushing, sieving to extract grains in the 125–250 µm size range, and heavy liquid separation at 2.9 g cm−3. This concentrate was then repeatedly passed through a magnetic separator at various settings to separate pure pyroxene from pyroxene–plagioclase aggregates (less magnetic) and oxide minerals (more magnetic). Remaining contaminant grains were then removed by handpicking under a microscope. At CRPG, samples were crushed and sieved to 150–800 µm, plagioclase was removed by heavy liquid separation at a density of 3.3 g cm−3, and then samples underwent magnetic separation and handpicking to improve the selection of pure pyroxenes. Based on inductively coupled plasma optical emission spectroscopy (ICP-OES) data (Tables S1 and S2), analyzed pyroxene separates were primarily clinopyroxene (augite).
3.2.2 Cosmogenic-3He analyses
3He concentrations in the Labyrinth bedrock core samples were measured at LDEO, BGC, and CRPG. For quality control, internal comparability, and interlaboratory calibration, we also measured helium isotopes in the CRONUS-P pyroxene reference material, which is derived from the NXP 93*52 surface sample (Blard et al., 2015; Schaefer et al., 2016b; Table 2). For all samples, we normalize the measured 3He concentrations to the accepted CRONUS-P value ((5.02 ± 0.05) × 109 atoms g−1; Tables 1 and 2; Blard, 2021; Blard et al., 2015). At all laboratories, relative measurement uncertainties for the Labyrinth core samples increased with depth owing to the decreasing 3He concentrations, ranging from 2 % in the uppermost sample to 4 % in the lowermost sample.
At LDEO, we measured helium isotopes in eight LDEO-prepared Labyrinth core samples. We extracted helium in two subsequent heating steps, 5 min at ∼900 ∘C and 15 min at 1350 ∘C in a resistance-heated double-vacuum furnace. Following purification with a charcoal-filled, liquid-nitrogen-cooled U trap and SEAS getter, the gas was cryo-trapped at 14 ∘C. The helium fraction was released at 45 ∘C, and 3He and 4He were measured by peak jumping in a MAP 215-50 (e.g., Winckler et al., 2005). Spectrometer sensitivity was determined using a Yellowstone helium standard (Murdering Mudpots) with a 3He 4He ratio of 16.45Ra (where Ra=(3He 4He). Blank corrections were <0.3 % (3He) and <0.6 % (4He) for the Labyrinth samples. Standards were reproducible within <2 %, and standard sizes ranged from ∼4.0 × 10−18–1.5 × 10−16 mol and 1.7 × 10−13–6.5 × 10−12 mol for 3He and 4He, respectively. At LDEO, the mean as well as standard deviation of the 3He concentrations measured in the CRONUS-P reference material at the same time as the Labyrinth core samples was (5.16 ± 0.19) × 109 atoms g−1 (n=5, coefficient of variance (CV) = 4 %; Table S3).
At CRPG, 34 measurements were made on 15 CRPG-prepared Labyrinth core samples, and 5 measurements were made on 5 BGC-prepared Labyrinth core samples. Sample extraction was realized by complete fusion at 1500 ∘C in our custom-made extraction furnace (Blard, 2021; Zimmermann et al., 2018). Typical blanks were (2.1 ± 1.4) × 10−20 mol of 3He and (1.9 ± 0.1) × 10−15 mol of 4He. Extracted gas was then purified, cryofocused at 8 K, and released at 75 K in a gigavolt (GV) split flight tube mass spectrometer to measure 3He and 4He abundances. The mass spectrometer sensitivity was established with the helium standard HESJ made by Matsuda et al. (2002). The helium pressure of the HESJ standard bottle has been calibrated against another reference gas, which has itself been cross-checked against independently calibrated air and pure helium standards of two different mass spectrometers at CRPG (Nancy) (Gayer et al., 2004; Blard et al., 2006). At CRPG, the CRONUS-P 3He concentrations, measured between March and April 2019, were (5.04 ± 0.12) × 109 atoms g−1 (n=8, CV = 2 %; Table S3).
At BGC, 32 measurements were made on 14 BGC-prepared Labyrinth core samples, and 5 measurements were made on 3 CRPG-prepared Labyrinth core samples for the purpose of interlaboratory comparison. Cosmogenic-3He measurements at BGC employ a laser “microfurnace” extraction system coupled to a MAP-215 mass spectrometer and are described in detail in Balter-Kennedy et al. (2020). Full process blanks measured by heating empty tantalum packets in the same way as the samples were 148 600 ± 4200 atoms of 3He (error-weighted mean of 12 measurements with a reduced chi-squared value of 1.1) and were not distinguishable from the Faraday cup measurement background for 4He. This is an unusually high process blank for 3He measurements and resulted from the reuse of vacuum components that had previously been part of an extraction system used for argon–argon dating. After additional investigation, these components were found to be contaminated with tritium derived from neutron-irradiated samples. The 3He background is therefore the result of 3He production by tritium decay and diffusive release from the metal components. Although this resulted in a comparatively large 3He background, 3He release during sample processing occurred at a constant rate, and the total contribution was strictly proportional to the duration of sample gas residence in certain sections of the extraction line, so variability in the blank could be minimized by automated control of extraction line timing. Therefore, even though the magnitude of the process blank is large compared to typical extraction systems, the uncertainty in the blank correction at BGC is comparable to other labs, and the overall effect on measurement precision is minimal. After completion of this series of measurements, the offending vacuum line components were replaced. At BGC, 3He concentrations measured in CRONUS-P at the same time as the Labyrinth core samples were (4.78 ± 0.08) × 109 atoms g−1 (n=5, CV = 2 %; Table S3).
For the surface samples, we used existing 3He measurements made at LDEO, described in Schaefer et al. (2006; Table 2). Although not used in our calculations, earlier 3He measurements were made and published from these samples at ETH Zurich and Potsdam (Niedermann et al., 2007; Schäfer et al., 1999). 3He measurement uncertainties for the surface samples range from 2 %–3 %. The 3He concentration in sample NXP 93*52, measured alongside the other surface samples and the same sample from which the CRONUS-P reference material was derived, is (5.21 ± 0.25) × 109 atoms g−1 (Schaefer et al., 2006).
3.2.3 Cosmogenic-10Be analyses
We extracted beryllium from clean pyroxene at LDEO using a procedure modified from the methods for beryllium extraction from quartz (e.g., Bromley et al., 2014; Kohl and Nishiizumi, 1992; Schaefer et al., 2009; https://www.ldeo.columbia.edu/res/pi/tcn/Lamont_Cosmogenic_Nuclide_Lab/Chemistry_files/LDEO_Be_Chemistry_ver.4.pdf, last access: 30 November 2022). The established procedure for extracting beryllium from quartz includes (1) addition of 9Be carrier, (2) sample dissolution, (3) ion exchange chromatography using anion and then cation exchange columns, (4) beryllium precipitation, (5) combustion, and (6) preparation of accelerator mass spectrometer (AMS) targets. Because of the high cation load present in pyroxenes, Eaves et al. (2018) used small sample sizes (∼2 g) and large resin volumes (20 mL) for cation exchange chromatography. Nevertheless, they concluded that reduction in the cation load prior to ion chromatography using a precipitation step would improve the extraction of beryllium from pyroxene. Here, we add a simple pH 8 precipitation step to reduce the cation load in our samples prior to ion exchange chromatography. At pH 8, Be, Al, and Fe precipitate from solution as hydroxides, Be(OH)2, Al(OH)3, and Fe(OH)2, while Ca and Mg should remain in solution (Ochs and Ivy-Ochs, 1997). We summarize the LDEO methodology for pyroxene here.
For beryllium extraction from pure pyroxene separates we first weighed and spiked 100–200 mg of pyroxene with ∼180 µg of 9Be using an LDEO carrier (Schaefer et al., 2009). The addition of a 9Be carrier contributed less than 5.7 × 103 atoms of 10Be, which is the average value of our process blanks. The small sample sizes were sufficient for these samples with high cosmogenic-nuclide inventories while minimizing the overall ion load. Samples were digested in concentrated HF and HNO3 and evaporated to dryness with two to three additions of perchloric acid to drive off fluorides. The resulting residue was taken up in 1 mL 6M HCl, transferred to 15 mL centrifuge tubes, and diluted with 10 mL of Milli-Q water. NH4OH was used to adjust the pH to 8, discarding the supernatant containing Ca, Mg, and Na and collecting the precipitate containing Be (and Al, Fe, and Ti).
We isolated beryllium using ion chromatography methods described by Kohl and Nishiizumi (1992). Given that most Ca and Mg were likely removed in the pH 8 precipitation step, we opted to use 2 mL of Bio-Rad 50W-X8 200–400 mesh resin for cation exchange based on the amount of Al in our samples (Table S1). Following cation exchange columns, the beryllium fraction was evaporated to dryness and then taken up in 4 mL of 1 % HNO3, transferred to 15 mL centrifuge tubes. From this solution, we precipitated Be(OH)2 by adjusting the pH to 9 with NH4OH. After pouring off the supernate, this precipitation step was repeated. We then performed three rinses of the precipitate with Milli-Q water adjusted to pH 8. The Be(OH)2 precipitates were noticeably larger than the blank for several samples (Fig. S3), indicating that we exceeded the capacity of the cation exchange resin and Al or another cation eluted with beryllium. For these samples, we performed a second round of cation exchange chromatography, also with 2 mL of resin. Following the second round of cation columns, the Be(OH)2 precipitates for all samples were similar in size to the blank, indicating that the second column step was successful in isolating beryllium.
The isolated beryllium was then combusted to form BeO, which we combined with Nb powder at an approximate BeO : Nb ratio of 2:3 by volume and loaded into stainless-steel AMS cathodes. Packed targets were sent to the Center for Accelerator Mass Spectrometry at Lawrence Livermore National Laboratory for 10Be 9Be measurement relative to the 07KNSTD standard with a 10Be 9Be ratio of 2.85 × 10−12 (Nishiizumi et al., 2007). Reported uncertainties in 10Be measurements include 1σ uncertainty in the AMS measurement, uncertainty in the blank correction, and error in the carrier concentration (1.5 %) propagated in quadrature.
10Be 9Be ratios in all 15 samples range from 4 × 10−15 to 6 × 10−13, with relative AMS uncertainties of <2 %–8 % (Table S4). 10Be 9Be ratios for all process blanks are on the order of 10−16, equating to 3000–10 500 atoms of 10Be (Table S5). Therefore, blank corrections for the surface samples are <0.5 % and between 1 %–7.3 % for the Labyrinth core samples.
3.3 Apparent exposure age and erosion rate calculations
We calculate apparent exposure ages and erosion rates using Version 3 of the online calculator described by Balco et al. (2008) and subsequently updated (http://hess.ess.washington.edu/math/v3/v3_age_in.html, last access: 30 November 2022). All calculations employ the “St” scaling method of Stone (2000) and Lal (1991). To calculate the 3He production rate, we use the primary 3He production rate dataset of Borchers et al. (2016) in Version 3 of the online calculator (120 atoms g−1 yr−1; Balco et al., 2008). Apparent exposure ages are calculated assuming zero erosion and equate to a minimum age for the sample. Apparent erosion rates assume infinite exposure time and represent a maximum erosion rate for the sample. Ferrar dolerite pyroxenes are known to contain non-cosmogenic 3He, which is most likely produced by neutron capture on Li via the reaction 6Li(n,α)3He (Ackert and Kurz, 2004; Andrews and Kay, 1982). In Ferrar dolerite, the total concentration of non-cosmogenic 3He has been measured in samples that are shielded from the cosmic-ray flux (Ackert, 2000; Kaplan et al., 2017; Margerison et al., 2005). Together, these measurements converge on (3.3 ± 1.1) × 106 atoms g−1 of non-cosmogenic 3He throughout this lithology (see discussion in Balco, 2020). Non-cosmogenic 3He therefore constitutes <1 % of the measured 3He in the surface samples, so we do not consider non-cosmogenic 3He significant when calculating apparent exposure ages or erosion rates. At depth in the Labyrinth core, however, non-cosmogenic 3He comprises as much as 10 % of the measured 3He. Therefore, we do include non-cosmogenic 3He when performing production rate calculations in Sect. 5.1.1 and 5.1.2.
The new 3He and 10Be data are shown in Tables 1 and 2 and in Figs. 3 and 4. Key features of these datasets are summarized below.
4.1 Cosmogenic-3He concentrations
Cosmogenic-3He concentrations normalized using CRONUS-P in the surface samples range from 0.50–5.87 × 109 atoms g−1, equating to apparent surface exposure ages of 1.2–6.3 Myr (Table 2). In the Labyrinth dolerite core, CRONUS-P-normalized 3He concentrations range from (4.75 ± 0.08) × 108 at the surface to (0.29 ± 0.01) × 108 at 164 cm depth (Table 3, Fig. 3). The 3He concentration of the surface sample equates to an apparent exposure age of 1.2 Myr or an apparent erosion rate of 43.8 cm Myr−1 (Table 2). Measured cosmogenic-3He concentrations in the Labyrinth core differ slightly among the three labs (Table 3), but normalizing to CRONUS-P brings the BGC-prepared and LDEO-prepared concentrations into agreement within ∼5 % (Fig. 3). The CRONUS-P-normalized 3He concentrations for the CRPG-prepared samples, however, are systematically lower than the LDEO-prepared and BGC-prepared samples (up to ∼15 % lower). This is true also for the CRPG-prepared samples that were measured at BGC. Higher-than-expected Al concentrations measured by ICP-OES in the CRPG-prepared pyroxene suggest that plagioclase remained in the CRPG-prepared samples (Tables S1 and S2). To confirm, we applied a mixing model to determine the percentage of pyroxene, plagioclase, and magnetite (a common accessory mineral in Ferrar dolerite) in the CRPG samples and found that the CRPG-prepared samples contain >10 % plagioclase (see Supplement). The contamination by plagioclase is the likely reason for the lower 3He concentrations in the CRPG-prepared samples because 3He is poorly retained in that mineral phase (Cerling, 1990). Therefore, we exclude the 3He measurements of the CRPG-prepared pyroxenes from further discussion. The observation that plagioclase-contaminated pyroxene samples yielded lower 3He concentrations further supports the use of HF etching as an effective method for producing pure pyroxene separates, as plagioclase is readily dissolved in HF (Bromley et al., 2014). Notably, the 4He concentrations were systematically higher in the non-etched BGC-prepared (and CRPG-prepared) samples than in the LDEO-prepared samples, which were HF-etched (Fig. S2).

Figure 33He concentrations from the Labyrinth core normalized to CRONUS-P. The CRPG-prepared samples were excluded from the fitting procedure as described in Sect. 5.1.1. The solid black line is an exponential curve showing expected spallation-produced 3He concentrations calculated using the surface 3He concentration and an attenuation length of 140 g cm−2. Below ∼40 cm depth, the measured 3He concentrations are greater than the spallation curve, presumably due to production by muons.
4.2 Cosmogenic-10Be concentrations
10Be concentrations in the six surface samples range from 1.02–5.06×107 atoms g−1, with corresponding uncertainties of ∼2 %. Nine 10Be concentrations between 24 and 164 cm depth in the Labyrinth bedrock core ranged from 5.21 × 106 atoms g−1 in the uppermost sample to 4.32 × 105 atoms g−1 in the lowermost sample (Table 3, Fig. 4). Our first 10Be measurement of the Labyrinth core sample LABCO-06 clearly deviates from the rest of the depth profile, although the reasons for this are unknown. A second measurement of a re-processed split of LABCO-06, however, agrees with the rest of the 10Be concentrations in the depth profile. Therefore, in the production rate calibration exercise described in Sect. 5.1.1, we use only the second measurement of LABCO-06. Total relative uncertainty (measurement error, blank correction, and error in the carrier concentration propagated in quadrature) increased from 3 %–9 % downcore.
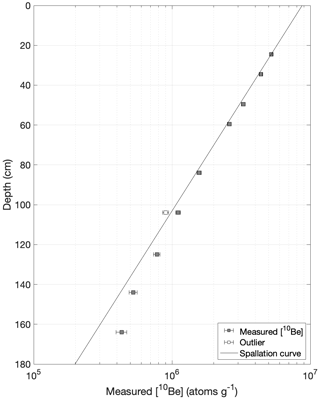
Figure 4Measured 10Be concentrations in pyroxenes from the Labyrinth core. All samples were prepared at LDEO, and 10Be 9Be ratios were measured at Lawrence Livermore National Laboratory (LLNL). The black line is an exponential curve showing the expected concentration of spallation-produced 10Be, calculated using the measured 10Be concentration at 24 cm depth and an attenuation length of 140 g cm−2. Below ∼100 cm depth, the measured 10Be concentrations are greater than the spallation curve, indicating production by muons.
Using a previously published production rate for 10Be in pyroxene of 3.6 atoms g−1 yr−1 (Eaves et al., 2018), the apparent 10Be exposure ages of the surface samples range from 1.0–4.4 Myr, and the apparent 10Be exposure age of the Labyrinth core surface is ∼830 kyr (surface 10Be concentration calculated by fitting an exponential curve to the 10Be data; therefore, surface 10Be age for the Labyrinth core is approximate).
4.3 General observations
Here, we highlight several key features of our dataset that inform the production rate estimations in Sect. 5.1. First, we observe that the apparent 3He and 10Be ages are discordant in surface samples 318, 444, 464, and 446S and the Labyrinth core surface (Table 2), suggesting that these samples have experienced complex exposure histories, potentially involving subaerial erosion or burial (e.g., by ice or sediment) or both. The canonical interpretation is that the geomorphic setting of these sample locations is consistent with a single period of exposure (Sect. 2), so a likely reason for this discordance is subaerial erosion. This observation requires that we consider erosion when attempting to estimate spallation and muon production rates in Sect. 5.1.
Figures 3 and 4 show that the measured 10Be and 3He inventories in the Labyrinth core exceed those predicted by a spallation curve below ∼100 cm depth and ∼40 cm depth, respectively, indicating that muon-produced 10Be and 3He make up a significant portion of the measured concentrations below these depths. With this finding, we present the first identification of in situ 10Be production by muons and further confirm the importance of quantifying muon production of 3He (Larsen et al., 2021). At the depth range of the Labyrinth core, negative-muon capture is the primary muon production pathway. Therefore, we can use these data to estimate the negative-muon cross-sections for 3He and 10Be in pyroxene (Sect. 5.1.1).
5.1 Production rate estimate
The goal of this section is to place limits on several key parameters associated with 10Be and 3He production in pyroxene. Here, we use our Labyrinth core data to estimate parameters associated with spallation production of 10Be and 10Be and 3He production by negative-muon capture. In addition to the Labyrinth core, we use the surface sample data to further refine the 10Be spallation production rate in pyroxene. After estimating a production rate for each sample, we combine our findings from the Labyrinth core and surface samples to arrive at a likely value for the 10Be spallation production rate.
5.1.1 Spallation and muon production in the Labyrinth core
We use the 10Be and 3He concentrations in pyroxenes from the Labyrinth core to estimate parameters associated with 10Be and 3He production. To do so, we apply a forward model, adapted from Balco et al. (2019) to include radioactive decay, that simulates the accumulation of cosmogenic 3He and 10Be by spallation and muon production with depth. We then estimate several parameters related to 10Be and 3He production in pyroxene by fitting the model to our measured 10Be and 3He concentrations.
Measured 3He includes cosmogenic 3He produced by neutron spallation, negative-muon capture, fast-muon interactions, and non-cosmogenic 3He:
N3, m (atoms g−1) is the measured 3He concentration, N3, sp (atoms g−1) is 3He produced by high-energy neutron spallation, N (atoms g−1) is 3He produced by negative-muon capture, and N3, μf (atoms g−1) is 3He produced by fast-muon reactions. N3, non-cosmo (atoms g−1) is non-cosmogenic 3He, which we consider to be (3.3 ± 1.1) ×106 atoms g−1 in Ferrar pyroxenes (see Sect. 3.3 and discussion in Balco, 2020).
In contrast, all the measured 10Be is cosmogenic, produced by spallation and muon interactions:
Cosmogenic-nuclide production by high-energy neutron spallation decreases exponentially with mass depth (Lal, 1991):
where z is mass depth below the surface (g cm−2), Pi, sp(0) is the surface production rate of a given nuclide (atoms g−1 yr−1), and Λsp is the effective attenuation length for spallation production in mass depth (g cm−2). Therefore, the concentration of spallation-produced 3He as a function of mass depth z is
where P is the reference production rate for 3He at sea-level high latitude (SLHL), SSt is the scaling factor using St scaling (Stone, 2000), t is the exposure duration (yr), ε is the surface erosion rate (g cm−2 yr−1), and τ is a variable of integration. The concentration of spallation-produced 10Be, a radionuclide, as a function of mass depth z is
where P is the SLHL reference production rate for 10Be, and λ10 is the decay constant for 10Be ( yr−1; Chmeleff et al., 2010; Fink and Smith, 2007; Korschinek et al., 2010).
We adopt production by negative-muon capture from Heisinger et al. (2002b) as
where is the muon stopping rate, fD is the probability that the negative muon does not decay in the K shell before capture by the nucleus, fC is the chemical compound factor, and is the probability that the nuclide of interest is produced after negative-muon capture by the target nucleus. For muon-produced 10Be, the target nucleus is O, and we aim to find the optimal value for , which should be the same as the value of this parameter calibrated in quartz (0.00191; Balco, 2017). For O in a Ferrar dolerite pyroxene with composition En34Fs25Wo42 (typical augite from a medium-grained dolerite; Zavala et al., 2011), fC=0.520 (von Egidy and Hartmann, 1982); fD is well known for O (0.1828; Suzuki et al., 1987). In contrast, 3He is produced in many negative-muon-capture reactions on a myriad of targets (see Table 3 in Heisinger et al., 2002b). Therefore, we estimate the entire term, which represents the overall probability that a negative muon produces 3He. The term should be similar to 0.0045, which is the sum of theoretical values for 3He and 3H producing reactions in standard rock (Nesterenok and Yakubovich, 2016).
Production by fast-muon interactions is taken from Heisinger et al. (2002a) as
Here, σ0,i is the cross-section for nuclide production by fast muons. Because the Labyrinth core does not extend to depths dominated by fast-muon production, meaning that we cannot estimate the fast-muon cross-sections with our dataset, we apply fast-muon cross-sections from other studies in our model. We take σ0,10 to be the same as quartz (0.280 µb; Balco, 2017) and σ0,3 to be 6.01 µb, calculated by fitting Eq. 8 to 3He measurements in pyroxene from a 300 m drill core of the Columbia River Basalt in Washington, USA (Larsen et al., 2021; see Supplement). Npyx is the number of target atoms per gram in standard basalt, assuming all elements are targets (2.74×1022 atoms g−1, average atomic mass 22), and NO, pyx is the number of atoms per gram of O (1.57 × 1022 atoms g−1, relevant for 10Be production) for a Ferrar dolerite pyroxene with composition En34Fs25Wo42 (Zavala et al., 2011). The remaining terms in these equations yield the integrated muon flux at a given mass depth over time for a prescribed surface erosion rate (see Heisinger et al., 2002a, for symbol definitions). We evaluate Eqs. (8) and (9) using the “Model 1A” MATLAB code of Balco (2017), with the parameter α set to 1 (see discussion in Borchers et al., 2016, and Balco, 2017).
Together, Eqs. (1)–(9) comprise a forward model that we use to predict 3He and 10Be concentrations in our core samples. We apply the known 3He production rate calculated using the primary production dataset of Borchers et al. (2016; see Sect. 3.3), so our model has seven unknown parameters: the exposure duration, t; the surface erosion rate, ε; the spallogenic 10Be production rate at sea-level high latitude (SLHL), P; the spallation attenuation length, Λsp; the probability that negative-muon capture creates 3He and 10Be, and (since fC and fD are known for 10Be for the target O), respectively; and a variable to account for the core measurement offset below 18 cm depth (see discussion in Sect. 3.1 regarding discrepancy between the drillers' measurements of the core barrel and the recovered core length). We fit our model by minimizing the χ2 misfit statistic, M:
where Ni, p is the predicted cosmogenic-nuclide concentration, Ni, m is the measured cosmogenic-nuclide concentration, σi, m is the associated measurement uncertainty, and σ3, non-cosmo is the uncertainty in the non-cosmogenic-3He concentration in Ferrar dolerite. We impose the constraint that all parameters in this fitting exercise must be greater than zero, except the variable accounting for the core measurement offset below 18 cm, which can have any value.
The exposure history of a sample is important for determining parameters associated with cosmogenic-nuclide production, as burial and erosion affect the accumulation of cosmogenic nuclides throughout the rock column. Previous work suggests that the Labyrinth has been largely undisturbed since the mid-Miocene (Lewis et al., 2006; Sect. 2). We thus assume that the Labyrinth core site has not experienced burial since the mid-Miocene. Erosion, however, must be considered. Erosion brings rock from lower in the rock column towards the surface. In eroding rock, therefore, the measured nuclide concentration at any given depth accumulated at a range of depths with varying contributions from each of the muon production pathways. Therefore, the muon cross-sections and erosion rates cannot be determined simultaneously since infinite combinations of the two could yield the measured nuclide concentrations.
Because we cannot estimate all unknown parameters at the same time, we consider two end-members that capture the possible ranges for the production rate parameters given our measured 10Be and 3He concentrations. In the first end-member scenario, we assume that the site has experienced a finite period of exposure, determined by the apparent 3He exposure age, and zero erosion. For the second end-member, we assume that the site has been exposed for a much longer time than the apparent exposure age (several 10Be half-lives) at a steady erosion rate. Based on those end-members we can place limits on the parameters associated with 10Be and 3He in pyroxene.
The steady-erosion end-member affords a maximum value for spallation production of 10Be. Solving Eq. (5) for P at the Earth's surface yields
As t→∞, P. Because ε must be between zero and ε3 (the steady erosion rate from the 3He data; Sect. 4.1), P must be between (N and N.
The opposite is true for parameters associated with negative-muon capture, where the steady-erosion end-member yields a minimum value for and , and the zero-erosion end-member yields a maximum. Erosion exposes rock that contains cosmogenic nuclides produced at depths where fast muons comprise the majority of production, meaning that, compared to the zero-erosion assumption, the steady-erosion assumption will yield cosmogenic-nuclide concentrations with a higher proportion produced by fast muons and a smaller proportion produced by negative-muon capture. Because we prescribe values for the fast-muon cross-sections, the negative-muon cross-section decreases in our steady-erosion model to accommodate the fast-muon-produced inventory that accumulated when the sample was deeper in the rock column. Therefore, the steady-erosion end-member yields minimum values for and , and the zero-erosion end-member will give maximum values for and . In sum, the zero-erosion end-member will produce a lower limit on the spallation production rate and an upper limit on parameters associated with nuclide production by negative-muon capture, and the steady-erosion end-member affords an upper limit on the spallation production rate and a lower limit on the negative-muon-capture parameters. The optimal values for the production parameters for each end-member are listed in Table 4.
Zero-erosion end-member
In the ε=0 cm yr−1 end-member, there remain six unknown parameters: t, P, Λsp, , and and a variable to account for the core measurement offset below 18 cm. The minimum value of the χ2 statistic, M, is 111 for 24 degrees of freedom (30 samples minus 6 fitting parameters), resulting in a reduced χ2 value of 4.6. Because the residuals do not appear systematic (Fig. 5), the likely reason for this high χ2 value is errors unaccounted for in the misfit statistic, such as the uncertainty associated with interlaboratory standardization.
The results of this fitting exercise are shown in Fig. 5. The best-fitting parameter value for the zero-erosion case is t=1.18 Myr, which agrees with the apparent 3He age at the surface (1.24 Ma; Sect. 4.1). Optimal values for spallation-related parameters in this model are P atoms g−1 yr−1 and Λsp=142 g cm−2. As discussed above, P should be a minimum in this end-member, and the optimal value of 2.82 is indeed at the low end of the P confidence interval found in Eaves et al. (2018; reference production rate of 3.6 ± 0.8 atoms g−1 yr−1 at sea-level high latitude). The fitted value for Λsp is close to other estimates of the spallation attenuation length in Antarctica (∼140 g cm−2; Borchers et al., 2016; Balco et al., 2019; Brown et al., 1992), although the attenuation length is expected to vary slightly for different nuclides and lithologies (Argento et al., 2015). The best-fitting value for the measurement offset below 18 cm is 2.12 cm.
The optimal values for parameters related to negative-muon capture in this scenario are and . Again, the zero-erosion end-member should yield maximum constraints for these parameters. The optimal value for is the same magnitude as for quartz (0.00191; Balco, 2017), while the value for is an order of magnitude higher than the expected value of 0.0045 for standard rock (Nesterenok and Yakubovich, 2016).
Steady-erosion end-member
For the steady-erosion end-member, we impose an exposure duration of 14.5 Myr based on 39Ar 40Ar ages of in situ ash deposits that suggest the Labyrinth formed by ∼14–15 Ma (Lewis et al., 2006; Sect. 2). With that assumption, the remaining free parameters are ε, P, Λsp, , and and the depth measurement offset below 18 cm. The same fit is achieved as the zero-erosion case, with a minimum value M=111 for 24 degrees of freedom (reduced χ2=4.6).
Figure 6 gives the results of the steady-erosion exercise. The optimal erosion rate over 14.5 Myr is 41.1 cm Myr−1, which agrees with the steady-state erosion rate calculated using the measured 3He concentration at the surface (Sect. 4.1). Under the steady-erosion assumption, the best-fitting P is 3.36 atoms g−1 yr−1, and the optimal Λsp is 144 g cm−2. Here, the estimate for P is an upper limit. Notably, the optimal P is close to the estimate of Eaves et al. (2018). The best-fitting value for the depth measurement offset below 18 is 2.05 cm.
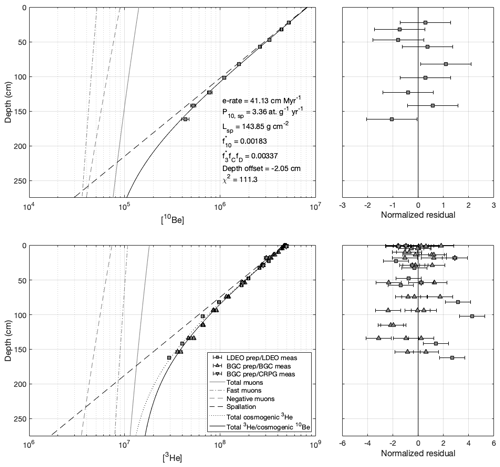
Figure 6Model results for Labyrinth core for the steady-erosion case. Optimal parameter values are shown in the text inset in the top left panel.
The optimal values for parameters related to negative-muon capture for the steady-erosion assumption are and . Here, the value for is nearly identical to for quartz (0.00191; Balco, 2017). In this scenario, however, the optimal is also the same magnitude as the expected value from standard rock (Nesterenok and Yakubovich, 2016). The fitted values for P, and for the steady-erosion end-member are closer to the expected values than for the zero-erosion end-member, and there is no geomorphic evidence against steady erosion taking place at the Labyrinth core site. Therefore, going forward, we assume steady erosion for the Labyrinth core and use the muon cross-sections derived under this assumption for calculating muon production rates.
5.1.2 Spallation production in the surface samples
Here, we derive upper and lower limits on the spallation production rate of 10Be in pyroxene using the 10Be and 3He concentrations of the six surface samples by again imposing the zero-erosion (lower limit) and steady-erosion (upper limit) end-members described in Sect. 5.1.1. All calculations of the muon production rates are made using the “Model 1A” MATLAB code of Balco (2017), with the parameter α set to 1 (Balco, 2017; Borchers et al., 2016), the fast-muon-reaction cross-sections described in Sect. 5.1.1, and the negative-muon-capture cross-sections resulting from the steady-erosion end-member for the Labyrinth core.
For the zero-erosion case, we solve the equation
for each sample. Here, t is the 3He apparent exposure age,
where Sthick is the sample thickness correction (dimensionless), and P3, μ is the total production rate by muons. For the sake of simplicity, we assume that the muon production rate at the center of the sample (sample thickness 2) is equivalent to P3, μ in the sample (Balco et al., 2008). We then calculate N10, μ by evaluating Eqs. (7) and (9) using the “Model 1A” MATLAB code for exposure duration t.
For the steady-erosion case, we assume that each surface has reached saturation with respect to spallation production and decay. To find the maximum P we solve the equation
for each sample. Here, the steady erosion rate ε is estimated for each sample by inverting our measured 3He concentrations using a forward model comprising Eqs. (1), (4), (6), and (8) and an exposure duration of 14.5 Myr. We again calculate the muon production rate at the sample midpoint and set Λsp=140 so that the only free parameter in the model is the erosion rate. We fit the model by minimizing the misfit statistic,
The optimal erosion rate is then used in Eq. (14) to solve for the upper limit on the 10Be spallation production rate.
Together, the zero-erosion and steady-erosion cases yield an allowable range for P given the measured cosmogenic-nuclide concentrations in each surface sample. We take the uncertainty in each value to be the 3He measurement error, 10Be measurement error, and the error in the 3He production rate (11 %) propagated in quadrature.
Figure 7 shows the resulting limits for P. The minimum values from the zero-erosion end-member range from 3.2–3.7 atoms g−1 yr−1, and the maximum values from the steady-erosion end-member range from 3.9–4.8 atoms g−1 yr−1. The overall production rate range encompassed by the surface samples (3.2–4.8 atoms g−1 yr−1) overlaps with the limits from the Labyrinth core (2.8–3.4 atoms g−1 yr−1).
5.1.3 Spallation production rate for 10Be in pyroxene
Now we combine the complementary information derived from the six surface samples and the Labyrinth core to define a summary distribution for P in pyroxene. The true value for P should fall somewhere between the highest of the lower limits and the lowest of the upper limits of the whole dataset. Therefore, we assume that there is a uniform probability for all production rate values that fall between these limits. To derive a summary distribution using this assumption, we perform a Monte Carlo simulation with 1E+05 iterations. Our summary distribution is described as
Here, x is any potential value for the 10Be production rate. P and P are lower and upper limits, respectively, on the 10Be production rate for sample j. For each Monte Carlo iteration n, P and P are randomly drawn from a normal distribution, with the mean and standard deviation of these values found in Sect. 5.1.1 and 5.1.2.
Figure 7 shows the resulting summary distribution. The distribution is approximately Gaussian, with a mean of 3.6 and a standard deviation of 0.2. Therefore, the likely value for the 10Be spallation production rate in pyroxene from our dataset is 3.6 ± 0.2 atoms g−1 yr−1. This agrees with the value of 3.6 ± 0.8 atoms g−1 yr−1, cross-calibrated with 3He for samples from the mid-latitudes (Eaves et al., 2018), but offers an improvement in the relative uncertainty in this value from ∼20 % to ∼5 %.
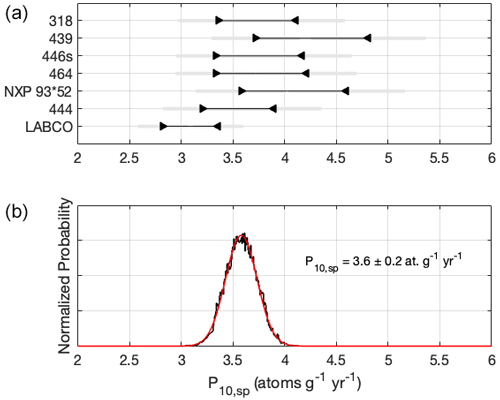
Figure 7Spallation production rate for 10Be in Ferrar dolerite pyroxene. (a) Minimum and maximum values for P10,sp. Gray lines show uncertainty in each value. (b) Summary distribution of P10,sp. The black line shows results from the Monte Carlo simulation described in Sect. 5.1.3. The red line shows the Gaussian distribution constructed using the mean and standard deviation from the Monte Carlo results. The text shows the most likely value for P10,sp given the summary distribution.
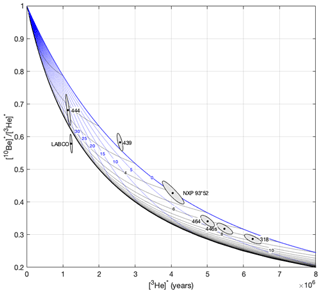
Figure 810Be–3He two-nuclide diagram. Asterisks indicate that nuclide concentrations have been normalized using site-specific production rates for each sample for ease of comparison across sampling locations. The x axis therefore represents apparent 3He years. Production by muons is not included, as a steady-erosion line that includes muons changes with elevation. Ellipses show 68 % confidence intervals based on measurement uncertainties. The 10Be concentration for the Labyrinth core surface (LABCO) sample is taken from the modeled surface concentration under the steady-erosion assumption for the Labyrinth core (Fig. 6) with a conservative 3 % uncertainty. Note that the LABCO concentrations would fall near a steady-erosion line drawn with muons included for elevation of the Labyrinth core, as the 10Be concentration was derived from the modeled steady-state-erosion end-member with 14.5 Myr of exposure. The top line (blue) bounding the steady-erosion island is the simple exposure line, and the bottom bounding line (black) is the steady-erosion line. Blue lines are lines of constant erosion, and black lines are lines of constant age. The diagram shows that measured 10Be and 3He concentrations in the surface samples are consistent with ∼2–8 Myr of exposure and ∼0–35 cm Myr−1 of erosion.
5.2 Applications for 10Be in pyroxene
Based on the presented spallation production rate of 3.6 ± 0.2 atoms g−1 yr−1, we now explore the potential of 10Be in pyroxene for quantifying ice-sheet and landscape change. On 106-year timescales, the relative precision of 10Be in pyroxene (∼2 %) allows for simultaneously resolving exposure ages and erosion rates using the 10Be–3He pair. Figure 8 shows a 10Be–3He two-nuclide diagram (e.g., Nishiizumi et al., 1991), constructed using our estimate for the spallation 10Be production rate in pyroxene. Our sample concentrations are located in distinct positions throughout the two-nuclide diagram, generally between the constant-exposure and steady-erosion lines, meaning that our samples have experienced a range of erosion rate–exposure duration combinations. With 3He alone, we found apparent (minimum) exposure ages of ∼1–6 Myr for the surface samples. Including 10Be shows that those data are better explained with ∼2–8 Myr of exposure at erosion rates of ∼0–35 cm Myr−1, highlighting the power of this novel two-nuclide approach in pyroxene.
Canonically, the Dry Valleys landscape formed ∼14.5 Myr ago and has been preserved by extremely low erosion rates since that time (e.g., Denton and Sugden, 2005; Lewis et al., 2006; Sect. 2). Yet, the oldest surface in our dataset is ∼8 Myr when considering erosion, with samples 444 and 439 having exposure ages closer to ∼2 Myr (except for the Labyrinth core, which we assume has been exposed for 14.5 Myr under steady erosion for the production rate calibration; Sect. 5.1.1). Although our dataset is limited, the fact that several samples have cosmogenic-nuclide concentrations inconsistent with 14.5 Myr of exposure may suggest that the Dry Valleys landscape is more dynamic than once hypothesized, involving either subaerial erosion, burial by ice, or both (Middleton et al., 2012). Applying the 10Be–3He pair in the Dry Valleys and across Antarctica, where much of the exposed rock is mafic Ferrar dolerite, will yield more accurate exposure histories for understanding ice-sheet and landscape change.
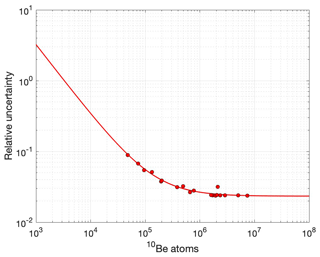
In addition to multi-nuclide applications, an obvious use of 10Be in pyroxene is surface exposure dating. At the sample sizes used in this study (0.1–0.2 g pyroxene), 10Be in pyroxene is an ideal exposure chronometer in landscapes like the Dry Valleys, where, owing to long exposure durations at low erosion rates, 10Be concentrations are high (∼106–107 atoms g−1). Applying 10Be in pyroxene for younger landscapes, however, would require increasing the sample size. Eaves et al. (2018) successfully extracted beryllium from 1–2 g of pyroxene using larger resin volumes for cation exchange chromatography than we used here, so an increase to 2 g (or more) of pyroxene is likely possible by combining our pH 8 precipitation step with slightly larger cation resin volumes. Using the relative uncertainties associated with our reported 10Be concentrations (Table S4, Sect. 3.2.3) and assuming 2 g to be a plausible larger sample size, we can estimate the relative uncertainties related to different exposure durations. To achieve relative uncertainties of ∼5 %, we would need to measure ∼1.2 × 105 atoms of 10Be (Fig. 9). At a sample size of 2 g, this equates to 6 × 104 atoms g−1, or ∼17 kyr at high-latitude sea level and ∼4 kyr at 2000 m elevation at high latitude. A threshold of 15 % uncertainty would require measurement of 3 × 104 atoms of 10Be, or, at 2 g of pyroxene, a 10Be concentration of 1.5 × 104 atoms g−1. This is equal to ∼4 kyr at high-latitude sea level or ∼1 kyr at 2000 m elevation at high latitude. A prime target area for applying 10Be in pyroxene to evaluate glacier change in the Late Holocene is the high-altitude Tropical Andes, where moraine boulders are derived from pyroxene-bearing lava flows (e.g., Bromley et al., 2011). Using 2 g of pyroxene from moraines at 4000 m elevation in the tropics would yield 5 % uncertainty for exposure ages of 2 kyr and 15 % uncertainty for exposure ages of 500 years. Importantly, the number of 10Be atoms associated with both of these uncertainty thresholds is greater than the average number of 10Be atoms in our blanks (5.7 × 103 10Be atoms; Table S5; other users will need to evaluate the limits of these methods for exposure dating given the average blank values from their own laboratories). Therefore, a relatively modest increase in the sample size used here would therefore make 10Be exposure dating in pyroxene useful in landscapes with Last Glacial Maximum to Late Holocene exposure ages.
We measured 10Be in Ferrar dolerite pyroxenes from the McMurdo Dry Valleys, Antarctica, with apparent 3He exposure ages of 1–6 Myr. To facilitate the beryllium isolation from pyroxene, we added a pH 8 precipitation to remove Ca, Mg, and Na, reducing the cation load prior to ion exchange chromatography. We also found that with ∼20 % sample dissolution through HF leaching, 10Be concentrations stabilized, suggesting complete removal of meteoric 10Be, even in our samples with 106-year exposure durations. Our 10Be 9Be ratios ranged from 5 × 10−13 to 4 × 10−15 for samples with 10Be concentrations from 4 × 10−15 to 6 × 10−13 atoms g−1, with relative uncertainties of 2 %–9 %. The average blank contained 5.7 × 103 atoms of 10Be, and blank corrections ranged from <1 % in the surface samples to 7 % at 1.6 m depth in the Labyrinth bedrock core. We derived a 10Be spallation production rate in pyroxene of 3.6 ± 0.2 atoms g−1 yr−1 using 10Be and 3He concentrations in the six surface samples and the Labyrinth drill core. Our analysis of the Labyrinth core also yields the first direct constraints of the cross-sections for 10Be and 3He production by negative-muon capture ( and 0.00337).
Given the measurement precision, the low-10Be laboratory blanks, and the production rate reported here, 10Be in pyroxene can now be applied for surface exposure dating, burial dating, and erosion quantification. For example, we estimate that surfaces exposed for 2 kyr at 4000 m in the Tropical Andes could be dated with 5 % uncertainty using our beryllium extraction methods for pyroxene. Furthermore, the application of the 10Be–3He pair in pyroxene reveals that our cosmogenic-nuclide concentrations in surface samples located throughout the Antarctic Dry Valleys are consistent with ∼2–8 Myr of exposure at 0–35 cm Myr−1, offering more insight into the ice-sheet and denudation histories of the Dry Valleys than does 3He alone. With this dataset, we observe that locations throughout the Dry Valleys have a range of exposure and erosional histories. Expanding the use of the 10Be–3He pair beyond surfaces that appear to be stable and to have experienced low erosion will yield further insight into this Antarctic landscape that is likely more dynamic than once hypothesized. In Antarctica and beyond, the 10Be–3He nuclide pair opens new opportunities for more accurately quantifying glacier and landscape histories in mafic rocks.
All analytical information associated with cosmogenic-nuclide measurements appear in the tables and Supplement. All MATLAB scripts used for model fitting and to generate the figures can be found at https://doi.org/10.5281/zenodo.8125448 (Balter-Kennedy and Balco, 2023).
The supplement related to this article is available online at: https://doi.org/10.5194/gchron-5-301-2023-supplement.
ABK, RS, GB, and BT carried out sample preparation. ABK and RS performed beryllium extraction. GB, GW, JL, LP, BT, and PHB performed helium analysis, and beryllium measurements were performed by AJH. ABK and GB performed data analysis. ABK prepared the manuscript with contributions from JMS, GB, RS, GW, JM, JLL, AJH, and PHB.
At least one of the (co-)authors is a member of the editorial board of Geochronology. The peer-review process was guided by an independent editor, and the authors also have no other competing interests to declare.
Publisher’s note: Copernicus Publications remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
We would like to acknowledge John Stone for kindly providing samples from the Labyrinth Core. This is LLNL-JRNL-842145, prepared in part by LLNL under contract DE-AC52-07NA27344. We would like to thank Dave Walker for help with calculating the mineral composition of the pyroxene samples.
This work is based upon work supported by the National Science Foundation Graduate Research Fellowship under grant no. DGE 2036197 to Allie Balter-Kennedy. Work at LDEO was supported in part by the NSF Office of Polar Programs (award no. 1744895 to Jennifer L. Lamp and Joerg M. Schaefer) and the NSF Division of Behavior and Cognitive Sciences (award no. 1853881 to Joerg M. Schaefer). Joerg M. Schaefer also received support from the Vetlesen Foundation. Work at BGC was supported by the Ann and Gordon Getty Foundation. CRPG funded helium analyses with the ANR JC EroMed (PI PH Blard, 2017-2022).
This paper was edited by Yeong Bae Seong and reviewed by Shaun Eaves and Mark Kurz.
Ackert, R. P.: Antarctic glacial chronology: new constraints from surface exposure dating, Doctoral thesis, Massachusetts Institute of Technology and Woods Hole Oceanographic Institution, Woods Hole Open Access Server, https://doi.org/10.1575/1912/4123, 2000.
Ackert, R. P. and Kurz, M. D.: Age and uplift rates of Sirius Group sediments in the Dominion Range, Antarctica, from surface exposure dating and geomorphology, Global Planet. Change, 42, 207–225, https://doi.org/10.1016/j.gloplacha.2004.02.001, 2004.
Andrews, J. N. and Kay, R. L. F.: Natural production of tritium in permeable rocks, Nature, 298, 361–363, https://doi.org/10.1038/298361a0, 1982.
Argento, D. C., Stone, J. O., Reedy, R. C., and O'Brien, K.: Physics-based modeling of cosmogenic nuclides part II – Key aspects of in-situ cosmogenic nuclide production, Quat Geochronol, 26, 44–55, https://doi.org/10.1016/j.quageo.2014.09.005, 2015.
Balco, G.: Production rate calculations for cosmic-ray-muon-produced 10Be and 26Al benchmarked against geological calibration data, Quat. Geochronol., 39, 150–173, https://doi.org/10.1016/j.quageo.2017.02.001, 2017.
Balco, G.: Noncosmogenic helium-3 in pyroxene and Antarctic exposure dating: https://cosmognosis.wordpress.com/2020/08/22/noncosmogenic-helium-3-in-pyroxene-and-antarctic-exposure-dating/, last access: 23 June 2022, 2020.
Balco, G. and Shuster, D. L.: 26Al–10Be–21Ne burial dating, Earth Planet. Sc. Lett., 286, 570–575, https://doi.org/10.1016/j.epsl.2009.07.025, 2009.
Balco, G. and Rovey, C. W.: Absolute chronology for major Pleistocene advances of the Laurentide Ice Sheet, Geology, 38, 795–798, https://doi.org/10.1130/g30946.1, 2010.
Balco, G., Stone, J. O., Lifton, N. A., and Dunai, T. J.: A complete and easily accessible means of calculating surface exposure ages or erosion rates from 10Be and 26Al measurements, Quat. Geochronol., 3, 174–195, https://doi.org/10.1016/j.quageo.2007.12.001, 2008.
Balco, G., Blard, P.-H., Shuster, D. L., Stone, J. O. H., and Zimmermann, L.: Cosmogenic and nucleogenic 21Ne in quartz in a 28-meter sandstone core from the McMurdo Dry Valleys, Antarctica, Quat. Geochronol., 52, 63–76, https://doi.org/10.1016/j.quageo.2019.02.006, 2019.
Balter-Kennedy, A. and Balco, G.: Code supporting Cosmogenic 10Be in pyroxene: laboratory progress, production rate systematics, and application of the 10Be–3He nuclide pair in the Antarctic Dry Valleys, Zenodo [code], https://doi.org/10.5281/zenodo.8125448, 2023.
Balter-Kennedy, A., Bromley, G., Balco, G., Thomas, H., and Jackson, M. S.: A 14.5-million-year record of East Antarctic Ice Sheet fluctuations from the central Transantarctic Mountains, constrained with cosmogenic 3Be, 10Be, 21Ne, and 26Al, The Cryosphere, 14, 2647–2672, https://doi.org/10.5194/tc-14-2647-2020, 2020.
Bindschadler, R., Vornberger, P., Fleming, A., Fox, A., Mullins, J., Binnie, D., Paulsen, S. J., Granneman, B., and Gorodetzky, D.: The Landsat Image Mosaic of Antarctica, Remote Sens Environ, 112, 4214–4226, https://doi.org/10.1016/j.rse.2008.07.006, 2008.
Blard, P.-H.: Cosmogenic 3He in terrestrial rocks: A review, Chem. Geol., 586, 120543, https://doi.org/10.1016/j.chemgeo.2021.120543, 2021.
Blard, P.-H., Pik, R., Lavé, J., Bourlès, D., Burnard, P. G., Yokochi, R., Marty, B., and Trusdell, F.: Cosmogenic 3He production rates revisited from evidences of grain size dependent release of matrix-sited helium, Earth Planet. Sc. Lett., 247, 222–234, https://doi.org/10.1016/j.epsl.2006.05.012, 2006.
Blard, P.-H., Bourlès, D., Pik, R., and Lavé, J.: In situ cosmogenic 10Be in olivines and pyroxenes, Quat. Geochronol., 3, 196–205, https://doi.org/10.1016/j.quageo.2007.11.006, 2008.
Blard, P.-H., Balco, G., Burnard, P. G., Farley, K. A., Fenton, C. R., Friedrich, R., Jull, A. J. T., Niedermann, S., Pik, R., Schaefer, J. M., Scott, E. M., Shuster, D. L., Stuart, F. M., Stute, M., Tibari, B., Winckler, G., and Zimmermann, L.: An inter-laboratory comparison of cosmogenic 3He and radiogenic 4He in the CRONUS-P pyroxene standard, Quat. Geochronol., 26, 11–19, https://doi.org/10.1016/j.quageo.2014.08.004, 2015.
Borchers, B., Marrero, S., Balco, G., Caffee, M., Goehring, B., Lifton, N., Nishiizumi, K., Phillips, F., Schaefer, J., and Stone, J.: Geological calibration of spallation production rates in the CRONUS-Earth project, Quat. Geochronol., 31, 188–198, https://doi.org/10.1016/j.quageo.2015.01.009, 2016.
Bromley, G. R. M., Hall, B. L., Schaefer, J. M., Winckler, G., Todd, C. E., and Rademaker, K. M.: Glacier fluctuations in the southern Peruvian Andes during the late-glacial period, constrained with cosmogenic 3He, J. Quat. Sci., 26, 37–43, https://doi.org/10.1002/jqs.1424, 2011.
Bromley, G. R. M., Winckler, G., Schaefer, J. M., Kaplan, M. R., Licht, K. J., and Hall, B. L.: Pyroxene separation by HF leaching and its impact on helium surface-exposure dating, Quat. Geochronol., 23, 1–8, https://doi.org/10.1016/j.quageo.2014.04.003, 2014.
Brown, E. T., Edmond, J. M., Raisbeck, G. M., Yiou, F., Kurz, M. D., and Brook, E. J.: Examination of surface exposure ages of Antarctic moraines using in situ produced 10Be and 26Al, Geochim. Cosmochim. Ac., 55, 2269–2283, https://doi.org/10.1016/0016-7037(91)90103-c, 1991.
Brown, E. T., Brook, E. J., Raisbeck, G. M., Yiou, F., and Kurz, M. D.: Effective attenuation lengths of cosmic rays producing 10Be and 26Al in quartz: Implications for exposure age dating, Geophys. Res. Lett., 19, 369–372, https://doi.org/10.1029/92gl00266, 1992.
Bruno, L. A., Baur, H., Graf, T., Schlüchter, C., Signer, P., and Wieler, R.: Dating of Sirius Group tillites in the Antarctic Dry Valleys with cosmogenic 3He and 21Ne, Earth Planet. Sc. Lett., 147, 37–54, https://doi.org/10.1016/s0012-821x(97)00003-4, 1997.
Burgess, S. D., Bowring, S. A., Fleming, T. H., and Elliot, D. H.: High-precision geochronology links the Ferrar large igneous province with early-Jurassic ocean anoxia and biotic crisis, Earth Planet. Sc. Lett., 415, 90–99, https://doi.org/10.1016/j.epsl.2015.01.037, 2015.
Cerling, T. E.: Dating geomorphologic surfaces using cosmogenic 3He, Quat. Res., 33, 148–156, https://doi.org/10.1016/0033-5894(90)90015-d, 1990.
Cerling, T. E.: Geomorphology and In-Situ Cosmogenic Isotopes, Annu. Rev. Earth Pl. Sc., 22, 273–317, https://doi.org/10.1146/annurev.earth.22.1.273, 1994.
Chmeleff, J., Blanckenburg, F. von, Kossert, K., and Jakob, D.: Determination of the 10Be half-life by multicollector ICP-MS and liquid scintillation counting, Nucl. Instruments Methods Phys. Res. Sect B., 268, 192–199, https://doi.org/10.1016/j.nimb.2009.09.012, 2010.
Denton, G. H. and Sugden, D. E.: Meltwater features that suggest Miocene ice-sheet overriding of the Transantarctic Mountains in Victoria Land, Antarctica, Geogr. Ann, Ser. Phys. Geogr., 87, 67–85, https://doi.org/10.1111/j.0435-3676.2005.00245.x, 2005.
Denton, G. H., Sugden, D. E., Marchant, D. R., Hall, B. L., and Wilch, T. I.: East Antarctic Ice Sheet Sensitivity to Pliocene Climatic Change from a Dry Valleys Perspective, Geogr. Ann, Ser. Phys. Geogr., 75, 155–204, https://doi.org/10.2307/521200, 1993.
Dunai, T. J.: Cosmogenic Nuclides, https://doi.org/10.1017/cbo9780511804519, 2010.
Eaves, S. R., Collins, J. A., Jones, R. S., Norton, K. P., Tims, S. G., and Mackintosh, A. N.: Further constraint of the in situ cosmogenic 10Be production rate in pyroxene and a viability test for late Quaternary exposure dating, Quat. Geochronol., 48, 121–132, https://doi.org/10.1016/j.quageo.2018.09.006, 2018.
Egidy, T. and von and Hartmann, F. J.: Average muonic Coulomb capture probabilities for 65 elements, Phys. Rev. A, 26, 2355–2360, https://doi.org/10.1103/physreva.26.2355, 1982.
Fink, D. and Smith, A.: An inter-comparison of 10Be and 26Al AMS reference standards and the 10Be half-life, Nucl. Instruments Methods Phys. Res. Sect B., 259, 600–609, https://doi.org/10.1016/j.nimb.2007.01.299, 2007.
Gayer, E., Pik, R., Lavé, J., France-Lanord, C., Bourlès, D., and Marty, B.: Cosmogenic 3He in Himalayan garnets indicating an altitude dependence of the 3He 10Be production ratio, Earth Planet. Sc. Lett., 229, 91–104, https://doi.org/10.1016/j.epsl.2004.10.009, 2004.
Goehring, B. M., Kurz, M. D., Balco, G., Schaefer, J. M., Licciardi, J., and Lifton, N.: A reevaluation of in situ cosmogenic 3He production rates, Quat. Geochronol., 5, 410–418, https://doi.org/10.1016/j.quageo.2010.03.001, 2010.
Gosse, J. C. and Phillips, F. M.: Terrestrial in situ cosmogenic nuclides: theory and application, Quat. Sci. Rev., 20, 1475–1560, https://doi.org/10.1016/s0277-3791(00)00171-2, 2001.
Granger, D. E.: A review of burial dating methods using 26Al and 10Be, in: In Situ-Produced Cosmogenic Nuclides and Quantification of Geological Processes: Geological Society of America Special Paper 415, edited by: Siame, L. L., Bourlès, D. L., and Brown, 1–16, https://doi.org/10.1130/2006.2415(01), 2006.
Heisinger, B., Lal, D., Jull, A. J. T., Kubik, P., Ivy-Ochs, S., Neumaier, S., Knie, K., Lazarev, V., and Nolte, E.: Production of selected cosmogenic radionuclides by muons 1. Fast muons, Earth Planet. Sc. Lett., 200, 345–355, https://doi.org/10.1016/s0012-821x(02)00640-4, 2002a.
Heisinger, B., Lal, D., Jull, A. J. T., Kubik, P., Ivy-Ochs, S., Knie, K., and Nolte, E.: Production of selected cosmogenic radionuclides by muons: 2. Capture of negative muons, Earth Planet. Sc. Lett., 200, 357–369, https://doi.org/10.1016/s0012-821x(02)00641-6, 2002b.
Hippe, K.: Constraining processes of landscape change with combined in situ cosmogenic 14C-10Be analysis, Quat. Sci. Rev., 173, 1–19, https://doi.org/10.1016/j.quascirev.2017.07.020, 2017.
Ivy-Ochs, S., Kubik, P. W., Masarik, J., Wieler, R., Bruno, L., and Schlüchter, C.: Preliminary results on the use of pyroxene for 10Be surface exposure dating, Schweiz, Mineral. Petrogr. Mitt., 78, 375–382, 1998.
Ivy-Ochs, S., Schlüchter, C., Kubik, P. W., Dittrich-Hannen, B., and Beer, J.: Minimum 10Be exposure ages of early Pliocene for the Table Mountain plateau and the Sirius Group at Mount Fleming, Dry Valleys, Antarctica, Geology, 23, 1007–1010, https://doi.org/10.1130/0091-7613(1995)023<1007:mbeaoe>2.3.co;2, 1995.
Kaplan, M. R., Licht, K. J., Winckler, G., Schaefer, J. M., Bader, N., Mathieson, C., Roberts, M., Kassab, C. M., Schwartz, R., and Graly, J. A.: Middle to Late Pleistocene stability of the central East Antarctic Ice Sheet at the head of Law Glacier, Geology, 45, 963–966, https://doi.org/10.1130/g39189.1, 2017.
Kohl, C. P. and Nishiizumi, K.: Chemical isolation of quartz for measurement of in-situ -produced cosmogenic nuclides, Geochim. Cosmochim. Ac., 56, 3583–3587, https://doi.org/10.1016/0016-7037(92)90401-4, 1992.
Kurz, M. D.: Cosmogenic helium in a terrestrial igneous rock, Nature, 320, 435–439, https://doi.org/10.1038/320435a0, 1986.
Kurz, M. D. and Brook, E. J.: Surface exposure dating with cosmogenic nuclides, in: Dating in exposed and surface contexts, 139–159, 1994.
Lal, D.: Production of 3He in terrestrial rocks, Chem Geology Isotope Geosci. Sect., 66, 89–98, https://doi.org/10.1016/0168-9622(87)90031-5, 1987.
Lal, D.: Cosmic ray labeling of erosion surfaces: in situ nuclide production rates and erosion models, Earth Planet. Sc. Lett., 104, 424–439, https://doi.org/10.1016/0012-821x(91)90220-c, 1991.
Lamp, J. L., Marchant, D. R., Mackay, S. L., and Head, J. W.: Thermal stress weathering and the spalling of Antarctic rocks, J. Geophys. Res.-Ea., 122, 3–24, https://doi.org/10.1002/2016jf003992, 2017.
Larsen, I. J., Farley, K. A., Lamb, M. P., and Pritchard, C. J.: Empirical evidence for cosmogenic 3He production by muons, Earth Planet. Sc. Lett., 562, 116825, https://doi.org/10.1016/j.epsl.2021.116825, 2021.
Lewis, A. R., Marchant, D. R., Kowalewski, D. E., Baldwin, S. L., and Webb, L. E.: The age and origin of the Labyrinth, western Dry Valleys, Antarctica: Evidence for extensive middle Miocene subglacial floods and freshwater discharge to the Southern Ocean, Geology, 34, 513–516, https://doi.org/10.1130/g22145.1, 2006.
Margerison, H. R., Phillips, W. M., Stuart, F. M., and Sugden, D. E.: Cosmogenic 3He concentrations in ancient flood deposits from the Coombs Hills, northern Dry Valleys, East Antarctica: interpreting exposure ages and erosion rates, Earth Planet. Sc. Lett., 230, 163–175, https://doi.org/10.1016/j.epsl.2004.11.007, 2005.
Matsuda, J., Matsumoto, T., Sumino, H., Nagao, K., Yamamoto, J., Miura, Y., Kaneoka, I., Takahata, N., and Sano, Y.: The 3He 4He ratio of the new internal He Standard of Japan (HESJ), Geochem J., 36, 191–195, https://doi.org/10.2343/geochemj.36.191, 2002.
Matsuoka, K., Skoglund, A., Roth, G., Pomereu, J. de, Griffiths, H., Headland, R., Herried, B., Katsumata, K., Brocq, A. L., Licht, K., Morgan, F., Neff, P. D., Ritz, C., Scheinert, M., Tamura, T., Putte, A. V. de, Broeke, M. van den, Deschwanden, A. von, Deschamps-Berger, C., Liefferinge, B. V., Tronstad, S., and Melvær, Y.: Quantarctica, an integrated mapping environment for Antarctica, the Southern Ocean, and sub-Antarctic islands, Environ Model. Softw., 140, 105015, https://doi.org/10.1016/j.envsoft.2021.105015, 2021.
McKelvey, B. C. and Webb, P. N.: Geological investigations in southern Victoria Land, Antarctica, New Zeal J. Geol. Geop., 5, 143–162, https://doi.org/10.1080/00288306.1962.10420116, 1962.
Middleton, J. L., Ackert, R. P., and Mukhopadhyay, S.: Pothole and channel system formation in the McMurdo Dry Valleys of Antarctica: New insights from cosmogenic nuclides, Earth Planet. Sc. Lett., 355, 341–350, https://doi.org/10.1016/j.epsl.2012.08.017, 2012.
Nespolo, M.: Reference Module in Earth Systems and Environmental Sciences, Encyclopedia of Geology, 2nd Edn., 287–296, https://doi.org/10.1016/b978-0-12-409548-9.12409-1, 2020.
Nesterenok, A. V. and Yakubovich, O. V.: Production of 3He in Rocks by Reactions Induced by Particles of the Nuclear-Active and Muon Components of Cosmic Rays: Geological and Petrological Implications, Arxiv, https://doi.org/10.48550/arxiv.1607.08770, 2016.
Niedermann, S., Schaefer, J. M., Wieler, R., and Naumann, R.: The production rate of cosmogenic 38Ar from calcium in terrestrial pyroxene, Earth Planet. Sc. Lett., 257, 596–608, https://doi.org/10.1016/j.epsl.2007.03.020, 2007.
Nishiizumi, K., Imamura, M., Caffee, M. W., Southon, J. R., Finkel, R. C., and McAninch, J.: Absolute calibration of 10Be AMS standards, Nucl. Instruments Methods Phys. Res. Sect. B., 258, 403–413, https://doi.org/10.1016/j.nimb.2007.01.297, 2007.
Nishiizumi, K., Klein, J., Middleton, R., and Craig, H.: Cosmogenic10Be, 26Al, and 3He in olivine from Maui lavas, Earth Planet. Sc. Lett., 98, 263–266, https://doi.org/10.1016/0012-821x(90)90028-v, 1990.
Nishiizumi, K., Kohl, C. P., Arnold, J. R., Klein, J., Fink, D., and Middleton, R.: Cosmic ray produced 10Be and 26Al in Antarctic rocks: exposure and erosion history, Earth Planet. Sc. Lett., 104, 440–454, https://doi.org/10.1016/0012-821x(91)90221-3, 1991.
Ochs, M. and Ivy-Ochs, S.: The chemical behavior of Be, Al, Fe, Ca and Mg during AMS target preparation from terrestrial silicates modeled with chemical speciation calculations, Nucl. Instruments Methods Phys. Res. Sect. B., 123, 235–240, https://doi.org/10.1016/s0168-583x(96)00680-5, 1997.
Schäfer, J. M., Ivy-Ochs, S., Wieler, R., Leya, I., Baur, H., Denton, G. H., and Schlüchter, C.: Cosmogenic noble gas studies in the oldest landscape on earth: surface exposure ages of the Dry Valleys, Antarctica, Earth Planet. Sc. Lett., 167, 215–226, https://doi.org/10.1016/s0012-821x(99)00029-1, 1999.
Schaefer, J. M., Faestermann, T., Herzog, G. F., Knie, K., Korschinek, G., Masarik, J., Meier, A., Poutivtsev, M., Rugel, G., Schlüchter, C., Serifiddin, F., and Winckler, G.: Terrestrial manganese-53 – A new monitor of Earth surface processes, Earth Planet. Sc. Lett., 251, 334–345, https://doi.org/10.1016/j.epsl.2006.09.016, 2006.
Schaefer, J. M., Denton, G. H., Kaplan, M., Putnam, A., Finkel, R. C., Barrell, D. J. A., Andersen, B. G., Schwartz, R., Mackintosh, A., Chinn, T., and Schlüchter, C.: High-Frequency Holocene Glacier Fluctuations in New Zealand Differ from the Northern Signature, Science, 324, 622–625, https://doi.org/10.1126/science.1169312, 2009.
Schaefer, J. M., Finkel, R. C., Balco, G., Alley, R. B., Caffee, M. W., Briner, J. P., Young, N. E., Gow, A. J., and Schwartz, R.: Greenland was nearly ice-free for extended periods during the Pleistocene, Nature, 540, 252–255, https://doi.org/10.1038/nature20146, 2016a.
Schaefer, J. M., Winckler, G., Blard, P.-H., Balco, G., Shuster, D. L., Friedrich, R., Jull, A. J. T., Wieler, R., and Schluechter, C.: Performance of CRONUS-P – A pyroxene reference material for helium isotope analysis, Quat. Geochronol., 31, 237–239, https://doi.org/10.1016/j.quageo.2014.07.006, 2016b.
Schaefer, J. M., Codilean, A. T., Willenbring, J. K., Lu, Z.-T., Keisling, B., Fülöp, R.-H., and Val, P.: Cosmogenic nuclide techniques, Nat. Rev. Meth. Prim., 2, 18, https://doi.org/10.1038/s43586-022-00096-9, 2022.
Stone, J. O.: Air pressure and cosmogenic isotope production, J. Geophys. Res. Sol.-Ea., 105, 23753–23759, https://doi.org/10.1029/2000jb900181, 2000.
Sugden, D. E., Marchant, D. R., Potter, N., Souchez, R. A., Denton, G. H., III, C. C. S., and Tison, J.-L.: Preservation of Miocene glacier ice in East Antarctica, Nature, 376, 412–414, https://doi.org/10.1038/376412a0, 1995.
Summerfield, M. A., Stuart, F. M., Cockburn, H. A. P., Sugden, D. E., Denton, G. H., Dunai, T., and Marchant, D. R.: Long-term rates of denudation in the Dry Valleys, Transantarctic Mountains, southern Victoria Land, Antarctica based on in-situ-produced cosmogenic 21Ne, Geomorphology, 27, 113–129, https://doi.org/10.1016/s0169-555x(98)00093-2, 1999.
Young, N. E., Lesnek, A. J., Cuzzone, J. K., Briner, J. P., Badgeley, J. A., Balter-Kennedy, A., Graham, B. L., Cluett, A., Lamp, J. L., Schwartz, R., Tuna, T., Bard, E., Caffee, M. W., Zimmerman, S. R. H., and Schaefer, J. M.: In situ cosmogenic 10Be–14C–26Al measurements from recently deglaciated bedrock as a new tool to decipher changes in Greenland Ice Sheet size, Clim. Past, 17, 419–450, https://doi.org/10.5194/cp-17-419-2021, 2021.
Zavala, K., Leitch, A. M., and Fisher, G. W.: Silicic Segregations of the Ferrar Dolerite Sills, Antarctica, J. Petrol., 52, 1927–1964, https://doi.org/10.1093/petrology/egr035, 2011.
Zimmermann, L., Avice, G., Blard, P.-H., Marty, B., Füri, E., and Burnard, P. G.: A new all-metal induction furnace for noble gas extraction, Chem. Geol., 480, 86–92, https://doi.org/10.1016/j.chemgeo.2017.09.018, 2018.