Technical note: In situ U–Th–He dating by ⁴He ∕ ³He laser microprobe analysis

In situ U–Th–He geochronology is a potentially disruptive technique that combines laser ablation inductively coupled plasma mass spectrometry (LA-ICP-MS) with laser microprobe noble gas mass spectrometry. Despite its potential to revolutionize (detrital) thermochronology, in situ U–Th–He dating is not widely used due to persistent analytical challenges. A major issue is that current in situ U–Th–He dating approaches require that the U, Th, and He measurements are expressed in units of molar concentration, in contrast with conventional methods, which use units of molar abundance. Whereas molar abundances can be reliably determined by isotope dilution, accurate concentration measurements are not so easy to obtain. In the absence of matrix-matched U–Th concentration standards and accurate He ablation pit measurements, the required molar concentration calculations introduce an uncertainty that is higher than the conventional method, an uncertainty that is itself difficult to accurately quantify. We present a solution to this problem by using proton-induced ³He as a proxy for ablation pit volume and by pairing samples with a standard of known U–Th–He age. Thus, the U–Th–He age equation can be solved using relative rather than absolute concentration measurements. Pilot experiments show that the new method produces accurate results. However, it is prone to overdispersion, which is attributed to gradients in the proton fluence. These gradients can be measured, and their effect can be removed by fixing the geometry of the sample and the standard during the proton irradiation.

1 Introduction

Conventional U–Th–He thermochronology is labour-intensive, especially for zircon. It involves (1) identifying suitable crystals under a binocular microscope, (2) measuring their three-dimensional size to estimate the fraction of helium lost through α-ejection (Farley et al., 1996; Ketcham et al., 2011), (3) packing the individual crystals into Pt or Nd “microfurnaces” (House et al., 2000), (4) degassing the crystals with a laser under ultra-high-vacuum conditions and analysing the released gas by noble gas mass spectrometry, (5) recovering the degassed grains from the microfurnaces and dissolving them in hydrofluoric acid with a Parr vessel, and (6) determining their U and Th content by isotope dilution inductively coupled plasma mass spectrometry (ICP-MS; Fig. 1a).

In situ U–Th–He laser microprobe analysis removes steps 2, 3, and 5 of this procedure, which potentially increases sample throughput whilst producing U–Pb double dates as a byproduct. This opens new research opportunities in detrital geochronology (Boyce et al., 2006, 2009; Vermeesch et al., 2012; Tripathy-Lang et al., 2013; Evans et al., 2015; Danišík et al., 2017). However, despite its appeal, the method has still not been widely adopted by thermochronologists nearly 2 decades after its initial development by Boyce et al. (2006). The slow uptake of in situ U–Th–He dating has several causes, one of which is accuracy.

Measuring helium concentration (in units of atoms per unit volume) requires accurate estimates of ablation pit volume. Unfortunately, laser ablation produces irregularly shaped ablation pits under ultra-high-vacuum conditions, making pit volume measurements difficult at best and inaccurate at worst. The accuracy of the U and Th concentration measurements cannot be guaranteed either due to a lack of matrix-matched concentration standards.

Vermeesch et al. (2012) proposed a simplified workflow that pairs the sample with a well-characterized reference material of known U–Th–He age, thereby removing the need for accurate U and Th concentration measurements. Evans et al. (2015) reformulated this “pairwise dating” approach in terms of a κ calibration factor. Given the U $/$ Si, Th $/$ Si, and He $/$ V ratio measurements of a standard of known age t, where V is the ablation pit volume, the U–Th–He age equation can be written as

$$\begin{array}{}\text{(1)}& \begin{array}{rl}\mathit{\kappa }\left[{\displaystyle \frac{\mathrm{He}}{V}}\right]& =\mathit{\{}\mathrm{8}{\displaystyle \frac{\mathrm{137.82}}{\mathrm{138.82}}}\left(e^{{\mathit{\lambda }}_{\mathrm{38}}t}-\mathrm{1}\right)+{\displaystyle \frac{\mathrm{7}}{\mathrm{138.82}}}\left(e^{{\mathit{\lambda }}_{\mathrm{35}}t}-\mathrm{1}\right)\mathit{\}}\left[{\displaystyle \frac{\mathrm{U}}{\mathrm{Si}}}\right]\\ & +\mathrm{6}\left(e^{{\mathit{\lambda }}_{\mathrm{32}}t}-\mathrm{1}\right)\left[{\displaystyle \frac{\mathrm{Th}}{\mathrm{Si}}}\right]\end{array},\end{array}$$

where κ serves a similar purpose to the J factor in ⁴⁰Ar $/$ ³⁹Ar geochronology (Merrihue and Turner, 1966) or the ζ calibration factor in fission track thermochronology (Hurford and Green, 1983).

Although this method solves many of the practical difficulties of in situ U–Th–He measurements, the need for ablation pit measurements remains. In its simplest form, the κ calibration approach assumes that the drill rate of the UV laser is the same for the sample and the standard. Interferometric pit depth measurements indicate that this is not the case. For example, Vermeesch et al. (2012) observed drill rate differences of 15 % even when identical laser settings were used to analyse different Sri Lanka zircon megacrysts. These drill rate differences were found to be roughly proportional to the Si sensitivity differences measured by laser ablation inductively coupled plasma mass spectrometry (LA-ICP-MS), suggesting that Si can be used as a “drill rate proxy” for the helium measurements.

Using Si as a proxy for pit depth works reasonably well for the samples of Vermeesch et al. (2012) but is imprecise and only works when samples and standards are analysed in the same analytical session with identical laser settings.

This paper presents a progress report for a different approach to pairwise U–Th–He dating using proton-induced ³He as a proxy for ablation pit volume (Fig. 1a). When zircon is irradiated with high-energy protons in a particle accelerator, spallation reactions of Zr, Si, and O produce a small but measurable amount of ³He (Shuster et al., 2004). If a sample and co-irradiated reference material have experienced the same proton fluence, then Eq. (1) can be replaced with

$$\begin{array}{}\text{(2)}& \begin{array}{rl}\mathit{\kappa }\left[{\displaystyle \frac{{}^{\mathrm{4}}\mathrm{He}}{{}^{\mathrm{3}}\mathrm{He}}}\right]& =\mathit{\{}\mathrm{8}{\displaystyle \frac{\mathrm{137.82}}{\mathrm{138.82}}}\left(e^{{\mathit{\lambda }}_{\mathrm{38}}t}-\mathrm{1}\right)+{\displaystyle \frac{\mathrm{7}}{\mathrm{138.82}}}\left(e^{{\mathit{\lambda }}_{\mathrm{35}}t}-\mathrm{1}\right)\mathit{\}}\left[{\displaystyle \frac{\mathrm{U}}{\mathrm{Si}}}\right]\\ & +\mathrm{6}\left(e^{{\mathit{\lambda }}_{\mathrm{32}}t}-\mathrm{1}\right)\left[{\displaystyle \frac{\mathrm{Th}}{\mathrm{Si}}}\right]\end{array}.\end{array}$$

The following sections summarize experimental tests of this simple idea. These experiments were carried out between 2014 and 2016 using financial support from the UK's Natural Environment Research Council (NERC; see Acknowledgements). The research funding ended, the research team was dissolved, and research priorities shifted so that the results of our work were never published. With this technical note, we would like to encourage others to continue where we left off using the lessons that we have learned.

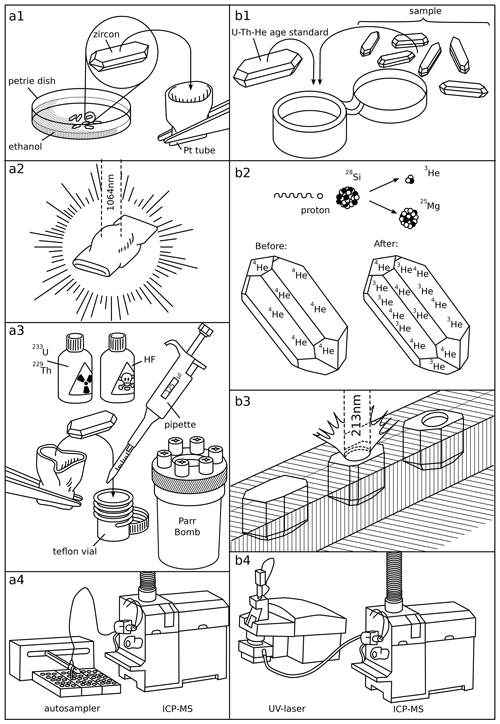
Figure 1 The analytical procedure for conventional U–Th–He dating (a) and the new in situ ⁴He $/$ ³He laser microprobe method (b): (a1) grain selection, (a2) degassing by laser heating in a Pt microfurnace, (a3) isotope dilution of U and Th, (a4) U and Th analysis in solution, (b1) packing sample and standard together, (b2) proton irradiation, (b3) ⁴He $/$ ³He analyses (of vertically mounted zircons) by UV laser microprobe noble gas mass spectrometry, (b4) U and Th analysis by LA-ICP-MS.

2 Experimental designs

We tested three different experimental designs.

1. Loose grains. Co-irradiate the sample and the standard in a plastic capsule (“rabbit”) without fixing or registering their position within the capsule (Sect. 2.1).

2. Vertically mounted grains. This experimental design is similar to the first one, but the grains are polished perpendicular to the c axis instead of parallel to it prior to laser ablation (Sect. 2.2).

3. Sample–standard “sandwiches”. Co-irradiate the sample and the standard in a fixed position and attached to each other (Sect. 2.3).

The three approaches were tested sequentially, which means that the second experimental design was motivated by the outcome of the first experiment, and the third experiment was motivated by the outcome of the second experiment. Sections 2.1 and 2.2 briefly discuss the methods and the results of the first two experiments. Section 2.3 describes the experimental set-up of the third experiment. In-depth discussions of the third method and its results are deferred to Sects. 3 and 4, respectively.

2.1 Loose grains

In the first set of experiments, loose grains of Fish Canyon zircon were packed together with Sri Lanka zircon LGC-1 (476.4 ± 5.7 Ma; Tian et al., 2017). After proton irradiation, the grains were mounted in Teflon; polished; and analysed for U, Th, and He using procedures that are detailed in Sect. 3. These experiments produced generally accurate, but highly dispersed results (Fig. 2). At first, we attributed this dispersion to compositional zoning of the Fish Canyon zircons (Fig. 3); because helium is measured in a separate ablation spot from the U and Th, any difference in actinide concentration between the two spots causes inaccurate ages.

Figure 2 The U–Th–He compositions of 61 Fish Canyon zircons (white ellipses) follow a bivariate normal U–Th–He distribution in log ratio space (Vermeesch, 2010). The mean composition corresponds to a U–Th–He age (the “central age”; Vermeesch, 2008) which is in excellent agreement with the known eruption age of the Fish Canyon Tuff (28.8 Ma; Kuiper et al., 2008). The compositional MSWD of 75 indicates significant overdispersion with respect to the formal analytical precision, likely due to a combination of compositional zoning (Fig. 3) and proton flux gradients. The data for this figure are provided in the Supplement.

2.2 Vertically mounted grains

Because compositional zoning tends to be largely concentric around the c axis, we carried out some experiments using vertically mounted Fish Canyon zircons (Fig. 3). This was achieved by (1) excavating a series of $\mathrm{100}\times \mathrm{50}\times \mathrm{50}$ µm “trenches” in sheets of Teflon, (2) placing proton-irradiated zircons in them, (3) covering the grains with a second sheet of Teflon, (4) welding the two sheets together by applying pressure to them on a hot plate at ca. 210 ^∘C, (5) polishing the edge of the resulting Teflon “sandwich” until the apexes of the grains were removed, and (6) placing the Teflon sheet upright in a bespoke sample holder. Helium was measured first, and after repolishing the U and Th were measured in a second ablation pit located down the c axis from the first one. This elaborate procedure slightly reduced the dispersion but unfortunately did not remove it.

Figure 3 Cathodoluminescence images of horizontally (a) and vertically (b) mounted Fish Canyon zircons, exhibiting predominantly c-axis concentric compositional zoning.

2.3 Sample–standard “sandwiches”

The previous pair of experiments indicated that, although compositional zoning may be one factor degrading the accuracy of in situ U–Th–He dating, it is not the dominant factor. Closer inspection of the standards revealed marked differences in ⁴He $/$ ³He ratios within and between Sri Lanka megacryst shards. These differences suggest the presence of strong, millimetre-scale gradients in the proton fluence despite the efforts taken to change the orientation of the samples during the irradiation.

To investigate this phenomenon and potentially fix it, we developed a third experimental design, in which the standard and sample are polished prior to irradiation and glued together along their polishing surfaces. This arrangement serves a dual purpose. First, it ensures that each point in the sample receives exactly the same proton dose as its counterpart in the standard. Second, by attaching the sample to the standard, any spallogenic ³He that passes through the polishing surface of the sample is injected into the standard and vice versa. This reduces potential geometric complications that may arise when comparing different sized crystals. We tested this approach using compositionally homogeneous GJ-1 (Jackson et al., 2004) as a sample to avoid the confounding effect of textural complexity in Fish Canyon zircon. The results of these experiments are described and discussed in the remainder of this paper.

3 Analytical methods and data processing

The sample–standard sandwiches were packed together in high-density propylene (HDPE) vials (Posthumus Plastics capsule type H and snap cap type E) and proton-irradiated at the Massachusetts General Hospital using procedures outlined by Shuster et al. (2004). Samples were attached to standards using superglue and were detached after irradiation by dissolution of the glue with acetone in an ultrasonic bath. The detached crystals were rinsed in de-ionized water and mounted in indium. Photographically identified contact points were used to match any location in the sample with its “mirror image” in the standard.

Helium was released from the zircon grains by ablation with a UP-213 frequency-quintupled Nd : YAG laser in a small (5 cm diameter) ablation cell with a sapphire window. Typical spot sizes were 90 µm in diameter, with ablation occurring at 20 Hz for 30 s. ⁴He was measured on a Faraday detector and ³He on a secondary electron multiplier (SEM) in peaking hopping mode (using either six or twenty 85 s cycles) on a Nu Instruments Noblesse sector field noble gas mass spectrometer at University College London. The extraction line of this instrument is described by Schwanethal (2015), as is the procedure to minimize the ¹²C³⁺ interference with ⁴He.

The ⁴He $/$ ³He ratio was obtained by linear regression of the ⁴He signals and ³He to “time zero”, which corresponds to the time when the cleaned gas was introduced into the ionization volume of the mass spectrometer. The resulting values have units of millivolts per hertz (mV Hz⁻¹). Note that these units vanish from the age equation after encapsulation in the κ calibration constant (Eq. 1). Thus, our method does not require the sensitivity of the Faraday and SEM detectors to be inter-calibrated.

The U and Th content of the samples was analysed by LA-ICP-MS at the Natural History Museum using an Agilent 8900 instrument that was coupled with a Teledyne Cetac Iridia laser. This set-up is optimized for raster imaging applications. Each grain was mapped using a 10×10 µm square spot with an energy density of 2.5 J cm⁻², a repetition rate of 400 Hz, and a scan speed of 400 µms⁻¹. ICP-MS measurements used dwell times of 2.5 ms for all measured isotopes (²⁹Si, ²⁰⁶Pb, ²³²Th, and ²³⁸U). NIST SRM610 was used as a concentration standard and 91500 zircon as a secondary reference material. Data reduction was done with Teledyne Cetac's HDIP software. This method allowed us to create U–Th maps with 10 µm horizontal resolution. These detailed maps allowed us to (1) detect any compositional zoning in the sample and standard and (2) interpolate the U–Th concentrations to the locations of the helium analysis spots.

This analytical protocol produces the following data files:

1. a table with the coordinates (x, y) of the helium ablation spots, the corresponding blank-corrected ⁴He $/$ ³He measurements, and their standard errors for both halves of the sample–standard sandwich (the coordinates can be expressed in LA-ICP-MS laser stage coordinates by identifying the helium ablation spots on the U–Th map);

2. two grids of U and Th concentration measurements or, equivalently, U $/$ Si and Th $/$ Si ratio measurements;

3. a table of fiducial points, recording the positions of at least three matching locations in the sample and the standard, recorded in LA-ICP-MS laser stage coordinates.

Given these three pieces of information, the U–Th–He ages are calculated as follows:

1. Map the coordinates of the standard onto those of the sample by Procrustes analysis, using the fiducial points (Fig. 4a–b).

2. Interpolate the U and Th concentration (or U $/$ Si and Th $/$ Si ratio) measurements to the locations of the ⁴He $/$ ³He measurements (Fig. 4c).

3. Calculate the κ calibration constant for each helium ablation spot in the standard given its known age and U, Th, and ⁴He $/$ ³He measurement.

4. Interpolate the κ values of the standard to the locations of the helium measurements in the sample.

5. Combine the κ parameter with the ⁴He $/$ ³He, U, and Th measurements of the sample to calculate the U–Th–He age (Fig. 4d–e).

4 Results

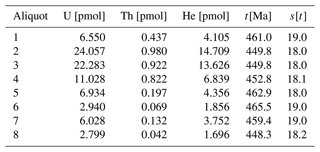
Inspection of the analytical results for two standard–sample pairs (Tables 1 and 2) reveals a number of patterns. First, the ⁴He $/$ ³He ratios vary significantly between different shards of LGC-1 and GJ-1. They are, on average, 25 % higher for the first pair than for the second pair. In contrast, the U and Th concentrations of the two pairs of shards are nearly identical. This discrepancy between the two sets of measurements can only have one cause, namely the presence of significant gradients in the proton fluence received by different parts of the “rabbit”. These gradients are reflected in the κ values, which vary in tandem with the ⁴He $/$ ³He measurements.

Whilst the κ values vary by a factor of 2 between the pairs, smaller gradients are visible within them. For example, pair 1 exhibits a ∼ 15 % difference in κ values over a distance of ∼ 500 µm. Fitting an interpolation surface to these values undoes the effect of the proton gradient and produces more accurate ages (Fig. 4c).

For pair 1, the in situ U–Th–He ages range from 420 to 520 Ma, with a central age of 453 ± 8 Ma, which is in good agreement with conventional U–Th–He ages of GJ-1 (456 ± 13 Ma; Table 3). The second pair yields equally accurate ages, ranging from 420 to 500 Ma, with a central value of 457 ± 24 Ma. The compositional mean squares of the weighted deviations (MSWDs, as defined by Vermeesch, 2010) of 1.5 for the first pair (Fig. 4e) and 2.3 for the second pair indicate that overdispersion is minor. Thus, the sandwich technique appears to have successfully removed the proton fluence gradient.

Figure 4 (a) Stage coordinates of the helium measurements for the standard (“L” is short for “LGC-1”) and sample (“G” is short for “GJ-1”) of the first sample–standard pair; (b) Procrustes transformation of the coordinates in the previous panel; (c) linear interpolation surface of the κ values for LGC-1; (d) U–Th–He age estimates for the first sample–standard pair (conventional age $=\mathrm{456.0}\pm \mathrm{12.7}$ Ma), with open circles representing the ages calculated using a uniform κ value; (e) U–Th–He compositions for the first sample–standard pair; (f) radial plot with the U–Th–He age estimates for the second sample–standard pair, with the third aliquot omitted as an outlier.

Table 1 Analytical results for the first pair of LGC-1 and GJ-1 shards. Row names represent helium laser ablation spots (LGC1-1-n and GJ1-1-n, where “n” is a number) and fiducial marks (LGC1-1-X and GJ1-1-X, where “X” is a letter). Columns x and y represent the raw LA-ICP-MS stage coordinates (in micrometres) of the helium spots; x^′ and y^′ are the coordinates after Procrustes transformation; ⁴He $/$ ³He and s[⁴He $/$ ³He] have units of millivolts per hertz; ³He has units of hertz; U, s[U], Th, and s[Th] have units of parts per million; κ and s[κ] have units of hertz per millivolt; and t and s[t] are in millions of years.

Table 2 Analytical results for the second pair of LGC-1 and GJ-1 shards. Row and column names follow the same convention as Table 1. The large uncertainties in the κ calibration constant of the sample are caused by the arrangement of the laser spots in two poorly aligned 1D arrays. These uncertainties have been omitted from the error propagation.

Table 3 Conventional U–Th–He data for GJ-1 zircon.

5 Discussion

The experiments reported in this paper are, in several ways, a best-case scenario. They compared two zircon megacrysts of similar age that are compositionally homogeneous. In fact, GJ-1 is so well behaved that it could also be used as a reference material for in situ U–Th–He dating. It remains to be seen if the method is equally successful when applied to more representative examples in which zircons are small and compositionally zoned.

The κ calibration method hinges on the availability of these well-characterized reference materials. They need to be available in sufficient quantities to be included with every proton irradiation. In this regard the method is similar to the ⁴⁰Ar $/$ ³⁹Ar method. In this study, we used LGC-1 as a reference material. However, the supply of this standard is limited. As mentioned in the previous paragraph, GJ-1 is also suitable as a reference material. Unfortunately it too is obtained from a single centimetre-sized crystal. It would be useful to identify a more abundant alternative. Tian et al. (2017) outline a workflow for doing so.

The most important requirement for an age standard is the absence of a distinct diffusion gradient. This, in turn, requires it to have resided under surface conditions for most of its existence after initial rapid cooling. Several Sri Lanka zircons appear to meet this requirement.

The sandwich method requires megacrystic standards, which are large enough to cover the entire sample (Fig. 5a). Finer-grained standards would need a different analytical design. One option would be to mount the polished sample and standard grains together prior to irradiation and attach them both to a cover slip made of glass or zirconia (Fig. 5b). Assuming that the proton beam intensity varies smoothly within the irradiation stack, the κ calibration constant could then be obtained by interpolation between the different aliquots of the standard.

The in situ ⁴He $/$ ³He method requires a sector field noble gas mass spectrometer, unlike the quadrupole instruments that dominate the field of U–Th–He thermochronology today. Combined with the need for proton irradiation, this makes the new method more expensive than the conventional approach. Nevertheless, we would argue that our approach merits further investigation because it opens the door to new avenues of research.

For example, by repeatedly alternating ⁴He $/$ ³He and U–Th measurements in a raster pattern on the same grain, it would be possible to create U–Th–He depth profiles or even reconstruct a three-dimensional U–Th–He image by ablating away the entire crystal, one layer at a time. This would allow the reconstruction of diffusion profiles and thermal history models equivalent to those obtained by ⁴He $/$ ³He step-heating experiments (Tripathy-Lang et al., 2015), but without the need to assume compositional homogeneity.

Although we used a high-end raster lasering system for our LA-ICP-MS experiments, U and Th concentrations could also be determined as individual spot measurements. We measured He first and U–Th later. However, it should also be possible to reverse this order. The collateral heating effect of UV laser ablation has been shown to be negligible (in apatite; van Soest et al., 2011) so that virtually no helium is lost during the U and Th measurements. Thus, it should be possible to measure U and Th first as individual spot measurements and revisit the same spots during subsequent helium extraction. This would remove step 2 (U–Th interpolation) of the data reduction procedure outlined in Sect. 3.

Although the pilot experiments were time-consuming, the proton irradiation approach offers the potential for high sample throughput. In contrast with conventional U–Th–He analysis, in which each individual zircon crystal must be handpicked and packaged, in situ analysis allows multiple zircons to be mounted together. Laser ablation is more easily automated (by pre-programming laser stage coordinates) than laser microfurnace heating (which additionally requires automated optical pyrometry). Data processing of in situ U–Th–⁴He $/$ ³He dating is also significantly easier than for other analytical approaches. It does not require spike calibration or ablation pit depth measurements. The data can be concisely summarized in simple tables (e.g. Table 1).

If the promise of increased throughput is fulfilled, then arguably the most important application for in situ U–Th–⁴He $/$ ³He thermochronology is in U–Th–He/Pb double-dating. Currently, detrital zircon U–Pb geochronology is the method of choice for sedimentary provenance analysis. However, in many places around the world, it is found that zircon U–Pb age spectra exhibit insufficient variability to resolve sedimentary provenance. For example, in the Sahara desert, essentially the same age spectra are found from Mauritania to Egypt (Pastore et al., 2021). The likely reason for this remarkable uniformity is recycling of older sandstones. Double-dating of detrital zircons offers a potential solution to this problem: the U $/$ Pb age would be controlled by the “protosource” of the sediment, whereas the U–Th–He age would be more sensitive to secondary resetting. U–Th–He $/$ Pb double-dating is very time-consuming using traditional methods, which require separate analysis for U–Pb and U–Th–He analysis (Reiners et al., 2005). In contrast, in situ methods produce U–Pb dates as a byproduct of the U–Th measurements, so double dates are generated “for free”.

Figure 5 Two ways to quantify and correct proton gradients: (a) the sample–standard “sandwich” method used in this work, where A and B are fiducial points, and (b) mounting the sample and the standard in Teflon and attaching them to a cover slip made of glass or zirconia. In both designs, the irradiation geometry is fixed so that it is possible to quantify proton flux gradients, and ejection of spallogenic ³He is balanced by injection from neighbouring sources.

6 Conclusions

This paper introduces a novel method for in situ U–Th–He geochronology that removes the need for absolute U, Th, and He abundance measurements. The new method is similar to the ⁴⁰Ar $/$ ³⁹Ar method in two ways. First, it co-irradiates samples with reference materials (“standards”) of known age. Second, it connects the sample to the standard using a calibration constant (J for ⁴⁰Ar $/$ ³⁹Ar, κ for in situ U–Th–⁴He $/$ ³He.

However, the analogy between ⁴⁰Ar $/$ ³⁹Ar and U–Th–⁴He $/$ ³He dating is not perfect. Whereas neutron-induced ³⁹Ar serves as a proxy for the parent nuclide (⁴⁰K), proton-induced ³He serves as a proxy for ablation pit volume. Therefore, unlike the ⁴⁰Ar $/$ ³⁹Ar method, in situ U–Th–⁴He $/$ ³He dating still requires the parent(s) and daughter to be measured separately. Although the measurements presented in this paper used U and Th concentrations in parts per million, the U–Th–⁴He $/$ ³He method also works with unprocessed U $/$ Si and Th $/$ Si measurements.

The results of the pilot experiment demonstrate that the new approach to in situ U–Th–He dating produces accurate results. However, further improvements are possible and, indeed, necessary. For example, a new generation of split flight tube noble gas mass spectrometers that are optimized for ⁴He $/$ ³He measurements could significantly increase precision and sensitivity (e.g. Brennan et al., 2020). Similar or even greater gains could be made by improving the proton irradiation protocol so that more atoms of proton-induced ³He are created per unit volume of zircon (Colleps et al., 2022). Together these improvements would allow a reduction in laser ablation spot size, which would create a proportional improvement in spatial resolution. Tweaking the proton irradiation protocol may also reduce the strength of the ³He concentration gradient. That, in turn, would simplify the analytical method and bring in situ U–Th–⁴He $/$ ³He dating closer to practical usability.