Calibration methods for laser ablation Rb–Sr geochronology: comparisons and recommendation based on NIST glass and natural reference materials

In situ rubidium–strontium (Rb–Sr) geochronology, using laser ablation–inductively coupled plasma–tandem mass spectrometry (LA-ICP-MS/MS) technology, allows rapid dating of K-rich minerals such as micas (e.g. biotite, muscovite, and phlogopite) and K-feldspar (potassium-containing feldspar). While many studies have demonstrated the ability of the method, analytical protocols vary significantly, and to date, no studies have provided an in-depth comparison and synthesis in terms of precision and accuracy. Here we compare four calibration protocols based on commonly used reference materials (RMs) for Rb–Sr dating. We demonstrate that downhole fractionation trends (DHFs) for natural biotite, K-feldspar, and phlogopite contrast with that for the commonly used Mica-Mg nano powder reference material. Consequently, Rb–Sr dates calibrated to Mica-Mg can be up to 5 % inaccurate, and the degree of inaccuracy appears to be unsystematic between analytical sessions. Calibrating to Mica-Mg also introduces excess uncertainty that can be avoided with a more consistent primary calibration material. We propose a calibration approach involving (1) NIST-610 glass as the primary reference material (PRM) for normalisation and drift correction and (2) a natural mineral with similar DHF characteristics to the analysed samples as matrix correction RM (MCRM) to correct the $\mathrm{Rb}/\mathrm{Sr}$ ratio for matrix-induced offsets. In this work, MDC phlogopite (the source mineral for Mica-Mg nano powder) was used as the MCRM, consistently producing accurate Rb–Sr dates for a series of natural biotites and K-feldspars with well-characterised expected ages. Biotite from the Banalasta Adamellite, Taratap Granodiorite, and Entire Creek pegmatite are also suitable RMs for $\mathrm{Rb}/\mathrm{Sr}$ ratio calibration purposes, with consistently <1.5 % fully propagated uncertainties in our methodological approach. Until calibration using isochronous natural standards as the primary RM becomes possible in data reduction software, the two-step calibration approach described here is recommended.

1 Introduction

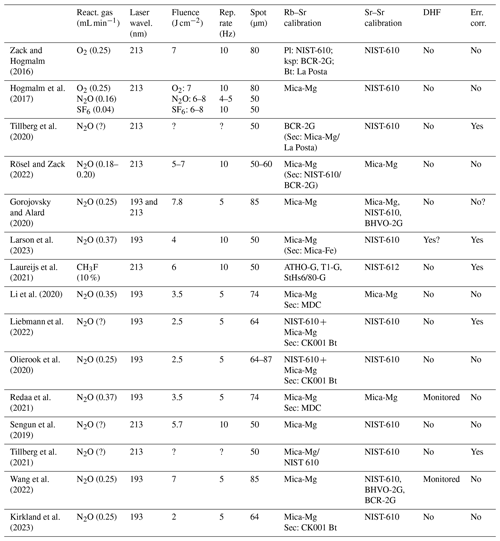
Rubidium–strontium (Rb–Sr) geochronology using laser ablation–inductively coupled plasma–tandem mass spectrometry (LA-ICP-MS/MS) has become a popular method to constrain the formation or cooling age of potassium-bearing minerals (Hogmalm et al., 2017; Laureijs et al., 2021; Redaa et al., 2021; Rösel and Zack, 2022; Tillberg et al., 2021, 2020; Wang et al., 2022; Liebmann et al., 2022; Zack and Hogmalm, 2016; Olierook et al., 2020; Larson et al., 2023; Li et al., 2020; Sengun et al., 2019; Gorojovsky and Alard, 2020; Kirkland et al., 2023; Jegal et al., 2022). In contrast to traditional Rb–Sr dating involving column chemistry in specialised laboratories, the laser ablation method allows rapid acquisition of Rb–Sr dates directly from thin sections or rock blocks with minimal sample preparation. The method involves the use of an ICP-MS/MS, equipped with a reaction cell in which isobaric isotopes can be chemically separated due to their significant differences in reactivity with an introduced reaction gas (Balcaen et al., 2015, and references therein). Applied to Rb–Sr geochronology, CH₃F, SF₆, O₂, and N₂O have been used as reaction gases (e.g. Zack and Hogmalm, 2016; Hogmalm et al., 2017; Moens et al., 2001), with the latter being the most widely used for quadrupole ICP-MS/MS due to its high reactivity. However, published analytical methodologies for LA-ICP-MS/MS Rb–Sr dating vary significantly beyond the applied reaction gas (Table 1). Reported laser conditions (fluence and repetition rate) are largely laser wavelength dependent, with common conditions being either ∼ 5–7 J cm⁻²/10 Hz for 213 nm lasers, especially during initial development work (e.g. Hogmalm et al., 2017; Zack and Hogmalm, 2016; Rösel and Zack, 2022; Laureijs et al., 2021; Sengun et al., 2019; Tillberg et al., 2020), or ∼ 2–4 J cm⁻²/5 Hz for 193 nm lasers (e.g. Redaa et al., 2021; Larson et al., 2023; Kirkland et al., 2023; Liebmann et al., 2022; Olierook et al., 2020; Li et al., 2020). The applied calibration protocols for mass discrimination and elemental fractionation, however, vary more significantly.

Table 1 Summary of published analytical conditions and protocols for LA-ICP-MS/MS Rb–Sr dating. Rep. rate is for laser repetition rate; Sec is for secondary reference material; Bt is for biotite; ksp is for K-feldspar; Pl is for plagioclase; and Err. Corr. is for error correlation calculated (in most cases based on calculated uncertainties after data reduction rather than during data reduction). In case of method development work, the best conditions are quoted.

We define three types of reference materials (RMs) in this work:

1. The primary RM (PRM) has a homogenous isotopic composition and is used for normalisation and drift correction.

2. The matrix correction RM (MCRM) has a heterogenous isotopic composition but well-known age and is used to correct the $\mathrm{Rb}/\mathrm{Sr}$ ratio for systematic matrix-induced offsets between the PRM and mineral samples.

3. The secondary RM (SRM) has a well-known age and a similar composition to the analysed samples and is used to verify the accuracy of the calibration protocol.

Most published work uses a glass reference material as PRM, with NIST-610 being most popular to correct for drift and calibrate the Sr isotopic ratios. $\mathrm{Rb}/\mathrm{Sr}$ ratios are most commonly calibrated against Mica-Mg, a phlogopite prepared as a pressed nano powder pellet, regardless of the analysed mineral (micas in most published work). However, the approach varies, with some methods directly calibrating to Mica-Mg as the PRM (e.g. Hogmalm et al., 2017; Rösel and Zack, 2022; Sengun et al., 2019; Gorojovsky and Alard, 2020; Wang et al., 2022; Li et al., 2020; Redaa et al., 2021) and others using NIST-610 as the PRM, followed by a correction for matrix-dependent fractionation against Mica-Mg as MCRM (e.g. Olierook et al., 2020; Liebmann et al., 2022). Secondary RMs, used to verify the accuracy of obtained dates, are either glass reference materials (e.g. Rösel and Zack, 2022; Larson et al., 2023; Laureijs et al., 2021) or in-house natural materials such as the La Posta biotite (Zack and Hogmalm, 2016), the MDC phlogopite (Redaa et al., 2021), or the CK001 biotite (Olierook et al., 2020).

In addition, laser-induced downhole fractionation (DHF) can occur during ablation and aerosol condensation processes and is most apparent when ratioing elements with contrasting volatilities (e.g. Longerich et al., 1996; Košler et al., 2005; Jackson and Günther, 2003). Elemental Sr is more refractory than the volatile Rb and hence has a high potential to fractionate during laser ablation (Zack and Hogmalm, 2016). A small number of studies have directly compared different calibration approaches and have described differences in Rb–Sr DHF behaviour between commonly used reference materials (e.g. Redaa et al., 2021; Wang et al., 2022). However, systematic comparisons between data reduction protocols, tested with natural materials, are limited in the current literature. Here, we compare four different calibration approaches for a series of natural biotite and K-feldspar (potassium-containing feldspar) samples. The samples were taken from quickly cooled igneous rocks, eliminating potential diffusion-related issues when comparing dates of different minerals. Hence, the well-constrained igneous crystallisation ages are the expected reference ages for the analysed samples, and one of the biotite samples has previously been dated by the Rb–Sr isotope dilution thermal ionisation mass spectrometry (ID-TIMS) method. The calibration approaches we compare are as follows:

• A.

  NIST-610 as the PRM for both ${}^{\mathrm{87}}\mathrm{Rb}{/}^{\mathrm{87}}\mathrm{Sr}$ and ${}^{\mathrm{87}}\mathrm{Sr}{/}^{\mathrm{86}}\mathrm{Sr}$ ratios plus MDC phlogopite as MCRM;

• B.

  NIST-610 as the PRM for both ${}^{\mathrm{87}}\mathrm{Rb}{/}^{\mathrm{87}}\mathrm{Sr}$ and ${}^{\mathrm{87}}\mathrm{Sr}{/}^{\mathrm{86}}\mathrm{Sr}$ ratios plus Mica-Mg pressed pellet as MCRM;

• C.

  Mica-Mg as the PRM for ${}^{\mathrm{87}}\mathrm{Rb}{/}^{\mathrm{87}}\mathrm{Sr}$ ratios and NIST-610 as the PRM for ${}^{\mathrm{87}}\mathrm{Sr}{/}^{\mathrm{86}}\mathrm{Sr}$ ratios; and

• D.

  Mica-Mg as the PRM for both ${}^{\mathrm{87}}\mathrm{Rb}{/}^{\mathrm{87}}\mathrm{Sr}$ and ${}^{\mathrm{87}}\mathrm{Sr}{/}^{\mathrm{86}}\mathrm{Sr}$ ratios.

We discuss the differences between these approaches in terms of accuracy and precision and highlight the importance of monitoring and correcting downhole fractionation with appropriate reference materials.

2 Sample descriptions

2.1 MDC phlogopite and Mica-Mg nano powder

Mica-Mg nano powder is used as a reference material for Rb–Sr dating. It consists of crushed phlogopite from Bekily (Madagascar), with a high Rb (1300 ± 40 µg g⁻¹) and low Sr (27 ± 3 µg g⁻¹) concentration (Redaa et al., 2023, and references therein). MDC is natural phlogopite, which was sourced from the same locality as Mica-Mg (Redaa et al., 2021). The reference age for both materials is 519.4 ± 6.5 Ma, and the initial ${}^{\mathrm{87}}\mathrm{Sr}{/}^{\mathrm{86}}\mathrm{Sr}$ ratio is 0.72607 ± 0.0007 (2 SE (standard error) uncertainties), constrained from a diopside (low-Rb mineral) that occurs in the same location (Hogmalm et al., 2017). However, for Mica-Mg some pellet-to-pellet variation in both $\mathrm{Rb}/\mathrm{Sr}$ and $\mathrm{Sr}/\mathrm{Sr}$ ratios has been observed (Redaa et al., 2023; Jegal et al., 2022).

2.2 Entire Creek pegmatite

The Entire Creek sample was taken from a deformed pegmatite in the Harts Range meta-igneous complex of central Australia, in the same location described by Mortimer et al. (1987). The pegmatite cross-cuts folded and foliated amphibolites is composed of coarse-grained quartz, plagioclase, alkali feldspar, and biotite, with the latter defining a strong axial-plane foliation to folds outlined by the pegmatite. Biotite and whole-rock $\mathrm{Rb}/\mathrm{Sr}$ and $\mathrm{Sr}/\mathrm{Sr}$ isotope ratios, obtained by ID-TIMS at the University of Adelaide, are reported in Mortimer et al. (1987) and define a seven-point (three biotite and four whole-rock analyses) isochron age of 312.1 ± 1.8/5.1 Ma (95 % confidence uncertainties, without/with overdispersion), recalculated in IsoplotR (Vermeesch, 2018), using the Villa et al. (2015) Rb–Sr decay constant of 1.3972 ± 0.0045 × 10⁻¹¹ a⁻¹ (File S1 in the Supplement).

2.3 Banalasta Adamellite (Bundarra Suite)

The S-type Banalasta Adamellite forms the southern end of the Bundarra Batholith in the southern New England Orogen in eastern Australia (e.g. Rosenbaum et al., 2012; Shaw and Flood, 1981; Flood and Shaw, 1975; Jeon et al., 2012). The Bundarra Batholith is an elongate north–south trending magmatic suite, spanning approximately 200 km. The Banalasta Adamellite is approximately 40 km in diameter and has sharp contacts with surrounding metasediments, with a contact metamorphic aureole characterised by a fine-grained cordierite-bearing assemblage at the pluton margin grading out to regional prehnite–pumpellyite metagreywacke assemblages over a distance of approximately 3 km (Flood and Shaw, 1977). Internally, the granite is massive, coarse-grained granitoid containing approximately equal proportions of K-feldspar and plagioclase, together with accessory apatite, zircon, and monazite. Biotite predominantly occurs in multi-grain clots, together with quartz, plagioclase, magnetite, zircon, and apatite. In rare cases, they contain relic garnet, suggesting that they formed from the hydration of garnet entrained from the granitic source region.

Melt-precipitated zircon from the Banalasta Adamellite gives zircon U–Pb ages of 286.2 ± 2.2 Ma (Black, 2007), 289.2 ± 1.7 Ma (Jeon et al., 2012) and 282 ± 4 Ma (Phillips et al., 2011). Whole-rock Rb–Sr data from the Bundarra Suite give an age of 285 ± 15 Ma ($n=\mathrm{6}/\mathrm{7}$; MSWD = 0.4). When additional feldspar Rb–Sr data are included in the isochron, then the isochron age is 283 ± 10 Ma ($n=\mathrm{9}/\mathrm{10}$; MSWD = 0.24) (File S2 in the Supplement). Both isochron dates were recalculated, using the data from Flood and Shaw (1977) and the decay constant from Villa et al. (2015). Additionally, Hensel et al. (1985) reported a model whole-rock Rb–Sr age of 287 ± 10 Ma for a group of 16 samples from the Bundarra Suite. Overall, it is evident that Rb–Sr age data are similar to the ages of melt precipitated zircon, consistent with the lack of evidence for extended fractional crystallisation (Jeon et al., 2012). The samples used in this study come from the same location as Black (2007) that has a granitic zircon of 286.2 ± 2.2 Ma, as well as a second location approximately 800 m away.

2.4 Taratap Granodiorite

The Taratap Granodiorite in the Delamerian Orogenic belt in southern Australia is classified as S-type calc-alkaline, with a composition dominated by microcline megacrysts (ca. 3–4 cm in length), which define a NNE-trending magmatic fabric in a coarse-grained groundmass of plagioclase, quartz, K-feldspar, and biotite, with accessory zircon, apatite, and monazite. Low-temperature alteration is evident in the thin section by the presence of chlorite–muscovite–titanite and minor allanite (Burtt and Abbot, 1998). The sample was chosen for analysis because the timing of the emplacement is tightly constrained by a zircon U–Pb ID-TIMS age of 497.11 ± 0.56 Ma (${}^{\mathrm{206}}\mathrm{Pb}{/}^{\mathrm{238}}\mathrm{U}$ weighted mean age; 95 % confidence interval uncertainty; MSWD = 1.8; n=6) and an apatite Lu–Hf age of 497.1 ± 5.5 Ma (MSWD = 1.1; n=38) (Glorie et al., 2024, and references therein).

3 Analytical methods

All Rb–Sr analyses were conducted at Adelaide Microscopy, University of Adelaide, using an Agilent 8900x ICP-MS/MS, coupled to a RESOlution-LR ArF excimer (193 nm) laser ablation system. A “squid” mixing device (Laurin Technic) was used to smooth the pulsed laser signal between the laser and the mass spectrometer. The instrument parameters follow those reported in Redaa et al. (2021), with ablation in a He atmosphere (350 mL min⁻¹) mixed with Ar (890 mL min⁻¹) as the carrier gas and N₂ (3.5 mL min⁻¹) added before the ICP torch to enhance the signal sensitivity. N₂O (0.37 mL min⁻¹) was used as the reaction gas to separate ⁸⁷Sr from ⁸⁷Rb. The ⁸⁶Sr and ⁸⁷Sr isotopes were measured as their oxide reaction products (e.g. ⁸⁷Sr¹⁶O), with a mass shift of 16 amu between the two quadrupole mass analysers (e.g. Q₁ = $m/z$ 87; Q₂ = $m/z$ 103). Despite the high reaction efficiency of ⁸⁷Sr, residual unreacted Sr prevents the direct measurement of ⁸⁷Rb. Instead, ⁸⁵Rb was measured as a proxy for ⁸⁷Rb and calculated, assuming natural isotopic abundance. The samples and reference materials were ablated using a circular laser beam of 67 µm diameter, a fluence of 3.5 J cm⁻², and repetition rate of 5 Hz. Further details are presented in Table 2. A total of three analytical sessions were conducted, with largely identical instrumental parameters between the different sessions. The ICP-MS was tuned to a sensitivity which kept Rb in pulse mode in Mica-Mg (the material with the highest Rb concentration), negating the requirement for additional pulse–analogue (P/A) corrections.

Table 2 Analytical conditions for the three LA-ICP-MS/MS sessions in this paper.

For each analytical session, NIST-610, Mica-Mg, and MDC were used as reference materials for calibration purposes. All data were processed in LADR (Norris and Danyushevsky, 2018), using an in-built data reduction algorithm that calculates error correlations (Pearson correlation coefficient) from the raw isotopic ratios for each sweep in an analysis in the same way as for U–Pb data reduction. Isotope ratios were calculated by (1) background subtraction; (2) correcting downhole fractionation (DHF) against the PRM; (3) averaging the DHF-corrected ratios of each sweep in the analysis; and then (4) normalising to the PRM to correct for matrix-independent instrument mass bias and drift. LADR applies a robust uncertainty propagation, using the total uncertainty budget of the measured quantified ratios. An example of an “uncertainty tree”, which can be queried for every analysis, is given in File S3 in the Supplement. The reader is referred to the LADR software manual (https://norsci.com/?p=ladr-support, last access: 23 August 2023) for further details.

Normalisation of the measured $\mathrm{Rb}/\mathrm{Sr}$ and $\mathrm{Sr}/\mathrm{Sr}$ ratios was conducted with two different reference materials (NIST-610 and Mica-Mg), following the four analytical protocols outlined above (1–4). The reference ${}^{\mathrm{87}}\mathrm{Rb}{/}^{\mathrm{87}}\mathrm{Sr}$ and ${}^{\mathrm{86}}\mathrm{Sr}{/}^{\mathrm{87}}\mathrm{Sr}$ ratios used for Mica-Mg were 83.4 ± 1.0 and 0.53981 ± 0.00070, respectively (Hogmalm et al., 2017). For NIST-610, the ${}^{\mathrm{87}}\mathrm{Rb}{/}^{\mathrm{87}}\mathrm{Sr}$ was calculated from concentration data (GeoREM-preferred values) as 3.28 ± 0.03, and for the ${}^{\mathrm{86}}\mathrm{Sr}{/}^{\mathrm{87}}\mathrm{Sr}$ ratio, the reference value of 1.409048 ± 0.000036 was used (Woodhead and Hergt, 2001). For each normalisation protocol, DHF corrections of the ${}^{\mathrm{87}}\mathrm{Rb}{/}^{\mathrm{87}}\mathrm{Sr}$ ratios were applied, based on the DHF behaviour of the applied PRM. No DHF correction was applied to the ${}^{\mathrm{86}}\mathrm{Sr}{/}^{\mathrm{87}}\mathrm{Sr}$ ratios. Where NIST-610 was used as the PRM, MDC phlogopite or Mica-Mg were used as MCRM to correct the ${}^{\mathrm{87}}\mathrm{Rb}{/}^{\mathrm{87}}\mathrm{Sr}$ ratios for matrix-dependent fractionation (cf. Roberts et al., 2017, for $\mathrm{U}/\mathrm{Pb}$ ratios; Simpson et al., 2022, for $\mathrm{Lu}/\mathrm{Hf}$ ratios).

All mica samples (including biotite samples and MDC phlogopite) were ablated, with the laser ablating parallel to cleavage. The Bundarra and Taratap samples were analysed in the thin section, and optical microscopy (birefringence) was used to only select ablation targets with upright (±10^∘) cleavage. The coarse Entire Creek biotites were mounted as mica books, using a vice to prevent air gaps between individual mica sheets, with the mica sheets mounted upright to expose multiple cleavage planes perpendicular to the surface.

For each sample and reference material, inverse isochron Rb–Sr dates (Li and Vermeesch, 2021) were calculated in IsoplotR (Vermeesch, 2018), based on the processed ${}^{\mathrm{87}}\mathrm{Rb}{/}^{\mathrm{87}}\mathrm{Sr}$ and ${}^{\mathrm{86}}\mathrm{Sr}{/}^{\mathrm{87}}\mathrm{Sr}$ ratios, their 2 SE uncertainties, and the calculated error correlations. Reported inverse isochron uncertainties are fully propagated 95 % confidence intervals, including the uncertainty about the decay constant and added uncertainty for overdispersion where required (calculated in IsoplotR). The exceptions are the inverse isochron dates for MDC and Mica-Mg when used as MCRMs, which are used to correct the $\mathrm{Rb}/\mathrm{Sr}$ ratios after calibrating to NIST-610. For these cases, the reported uncertainties are 95 % confidence uncertainties without external uncertainties (as the external uncertainties would otherwise be applied twice to the isochron dates of the analysed samples). Session-dependent correction factors (CFs) were calculated from the measured ${}^{\mathrm{87}}\mathrm{Rb}{/}^{\mathrm{87}}\mathrm{Sr}$ ratio for MDC and Mica-Mg (after drift corrections) and compared to the reference value (calculated from the published age for both MDC and Mica-Mg of 519.4 ± 6.5 Ma; Hogmalm et al., 2017; Redaa et al., 2021). These CF values (= measured ratio $/$ expected ratio) were subsequently applied to each unknown analysis when calibrated to either MDC or Mica-Mg. Finally, the uncertainties about the MDC and Mica-Mg dates are propagated to the reported Rb–Sr isochron uncertainties for each NIST-610 calibrated sample, using the quadratic addition of the relative uncertainties.

4 Results

4.1 Downhole fractionation trends

In this section, we compare the downhole fractionation (DHF) trend of the ${}^{\mathrm{87}}\mathrm{Rb}{/}^{\mathrm{87}}\mathrm{Sr}$ ratio between the analysed feldspars and micas and the reference materials (NIST-610 and Mica-Mg) (Fig. 1). The obtained fractionation trends do not vary significantly between different sessions; however, data from analytical session 3 are presented, as this session contains data for all analysed samples presented in this paper. The DHF trends were calculated in LADR, and individual scatterplots can be found in File S4 in the Supplement. As shown, The DHF trends for the analysed biotite, phlogopite, and K-feldspar samples are internally consistent, showing ∼ 10 % increase in the $\mathrm{Rb}/\mathrm{Sr}$ ratio over the first 20 s of ablation, followed by a flatter trend in the subsequent 20 s. NIST-610 shows a similar trend of the increasing $\mathrm{Rb}/\mathrm{Sr}$ ratio with ablation time; however, the amplitude of the DHF curve is more subdued compared to the natural samples (∼ 3.5 % increase in the first 20 s of ablation). In contrast, the DHF pattern for Mica-Mg shows an oscillating trend, increasing for the first ∼ 10 s of ablation and then dropping for the subsequent ∼ 30 s of ablation (Fig. 1).

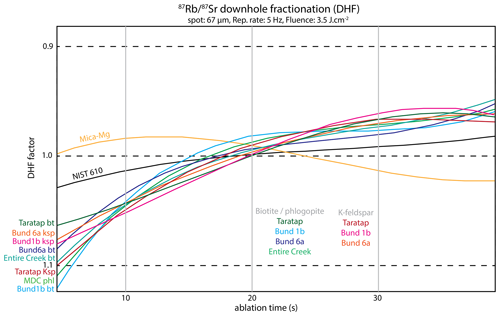
Figure 1 ${}^{\mathrm{87}}\mathrm{Rb}{/}^{\mathrm{87}}\mathrm{Sr}$ downhole fractionation profiles for the analysed reference materials Mica-Mg (yellow line) and NIST-610 (black line), the biotite/phlogopite (green–blue lines), and K-feldspar (red–pink lines) samples in analytical session 3, as calculated in LADR (Norris and Danyushevsky, 2018). The DHF factor is calculated relative to the average ratio of the ablation signal (i.e. DHF factor of 1 = average ${}^{\mathrm{87}}\mathrm{Rb}{/}^{\mathrm{87}}\mathrm{Sr}$ ratio of the downhole signal).

4.2 Within-session reproducibility of ${}^{\mathrm{87}}\mathrm{Rb}{/}^{\mathrm{87}}\mathrm{Sr}$ and ${}^{\mathrm{86}}\mathrm{Sr}{/}^{\mathrm{87}}\mathrm{Sr}$ ratios

Figure 2 shows the within-session variability (prior to drift correction) of the ${}^{\mathrm{87}}\mathrm{Rb}{/}^{\mathrm{87}}\mathrm{Sr}$ and ${}^{\mathrm{86}}\mathrm{Sr}{/}^{\mathrm{87}}\mathrm{Sr}$ ratios for both PRMs NIST-610 and Mica-Mg in analytical session 3. The reference materials are considered homogenous in both isotopic ratios, meaning that any variations are purely due to differences in the ablation characteristics from spot to spot. As shown, the measured ${}^{\mathrm{87}}\mathrm{Rb}{/}^{\mathrm{87}}\mathrm{Sr}$ ratios and ${}^{\mathrm{86}}\mathrm{Sr}{/}^{\mathrm{87}}\mathrm{Sr}$ ratios are significantly more consistent for NIST-610 compared to Mica-Mg (both measured using the same analytical conditions and spot size). The maximum within-session variability (= min–max range) in the ${}^{\mathrm{87}}\mathrm{Rb}{/}^{\mathrm{87}}\mathrm{Sr}$ ratio is <3 % for NIST-610, compared to >8 % for Mica-Mg. The ${}^{\mathrm{86}}\mathrm{Sr}{/}^{\mathrm{87}}\mathrm{Sr}$ ratio is more consistent for both RMs; however, the uncertainty about individual analyses is approximately 3× larger for Mica-Mg compared to NIST-610. ICP-MS mass bias drift is minimal for both isotope ratios in NIST-610, with only a slight increase in the $\mathrm{Rb}/\mathrm{Sr}$ ratio over the first 2–3 h of analysis. As both Mica-Mg and NIST-610 were analysed sequentially in the same analytical session, the apparent “drift” in the Mica-Mg ${}^{\mathrm{86}}\mathrm{Sr}{/}^{\mathrm{87}}\mathrm{Sr}$ ratios is due to variations in ablation rather than changes in the ICP-MS mass bias.

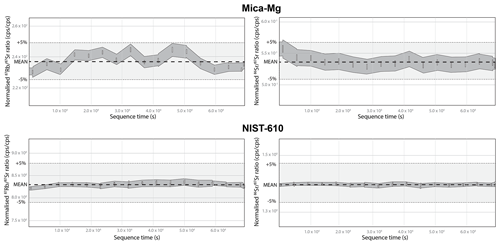
Figure 2 Variability in the ${}^{\mathrm{87}}\mathrm{Rb}{/}^{\mathrm{87}}\mathrm{Sr}$ and ${}^{\mathrm{86}}\mathrm{Sr}{/}^{\mathrm{87}}\mathrm{Sr}$ ratios for the analysed reference materials NIST-610 and Mica-Mg over the total duration of analytical session 3 (prior to drift correction). All plots are scaled equally to ± 5 % variation in the mean to aid visual comparisons. The vertical bars are ± 1 standard deviation. The grey envelopes model ± 2 standard deviations (note that for NIST-610, each standard was measured twice at each standard bracket).

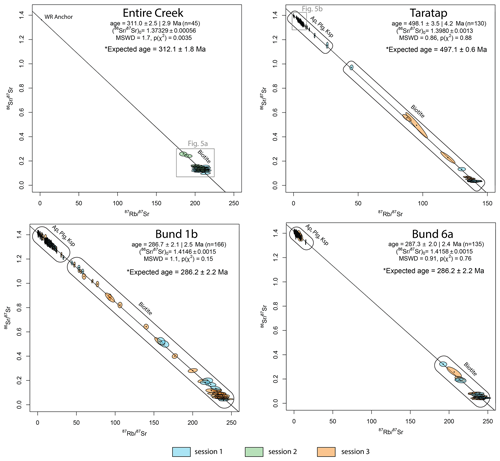
Figure 3 Pooled multi-mineral Rb–Sr isochron dates for the Entire Creek, Taratap, and the two Bundarra samples (Bund 1b and Bund 6a). The data were calibrated against NIST-610 as PRM and MDC as MCRM (see text for details). The colour code refers to the analytical session during which the data were obtained. Biotite analyses plot towards the radiogenic lower intercept of the inverse isochrons, while feldspar and apatite anchor $\mathrm{Rb}/\mathrm{Sr}$ ratios plot towards the low-radiogenic end of the isochron regression. All plots were calculated in IsoplotR (Vermeesch, 2018), reporting 95 % confidence interval uncertainties (including the uncertainty about the decay constant) with and without propagated uncertainty from the MDC MCRM. Expected ages are the recalculated Rb–Sr age from Mortimer et al. (1987), with the Villa et al. (2015) decay constant for the Entire Creek sample, the zircon U–Pb ID-TIMS age reported in Glorie et al. (2024) for the Taratap sample, and the zircon SHRIMP U–Pb age from Black (2007) for the Bundarra samples (see text for further details).

4.3 Isochron Rb–Sr dates for natural K-feldspars and micas

Inverse isochron plots and resulting Rb–Sr dates are presented for each analytical protocol in File S5 in the Supplement. Summary plots are shown in Fig. 3. The data table with the input ${}^{\mathrm{87}}\mathrm{Rb}{/}^{\mathrm{87}}\mathrm{Sr}$ and ${}^{\mathrm{86}}\mathrm{Sr}{/}^{\mathrm{87}}\mathrm{Sr}$ ratios is accessible from Figshare via the link in the Data availability section at the end of the paper. For the Bundarra samples, the biotite isochrons are anchored to apatite $\mathrm{Rb}/\mathrm{Sr}$ ratios, given that the apatites commonly occur as inclusions within biotite. For the K-feldspars, the isochrons are anchored to plagioclase, given that the analysed K-feldspars often show minor exsolution with plagioclase. However, the choice of anchoring mineral gives no difference in the obtained biotite and K-feldspar inverse isochron $\mathrm{Rb}/\mathrm{Sr}$ dates. For the Taratap sample, isochron anchoring was conducted to a combination of plagioclase and apatite in session 1 but only plagioclase in sessions 2 and 3, given the limited occurrence of apatite in the thin section. For the Entire Creek biotite sample, anchoring was conducted to whole-rock ${}^{\mathrm{86}}\mathrm{Sr}{/}^{\mathrm{87}}\mathrm{Sr}$ ratios from Mortimer et al. (1987). The MDC and Mica-Mg isochrons were anchored to an initial ${}^{\mathrm{86}}\mathrm{Sr}{/}^{\mathrm{87}}\mathrm{Sr}$ ratio of 1.3773 ± 0.0013 and calibrated to the published age of 519.4 ± 6.5 Ma (Hogmalm et al., 2017; Redaa et al., 2021).

The summary of obtained inverse Rb–Sr dates is presented in Table 3. As shown, there is only marginal variation in the absolute biotite dates between the three analytical protocols involving Mica-Mg, either as the PRM for $\mathrm{Rb}/\mathrm{Sr}$ ratios (protocols C and D) or as a MCRM (protocol B). Hence, in order to evaluate the accuracy of the obtained Rb–Sr dates against the expected references ages for each sample, we only compare the first two analytical protocols (NIST-610 as the PRM and either (A) MDC or (B) Mica-Mg as MCRM).

Table 3 Summary table of Rb–Sr dates obtained in this study. S is the session number, n is the number of analysed grains, and exp. age is the expected reference age (see below). All uncertainties are 95 % confidence intervals and are reported as (1) excluding external uncertainty (on the decay constant), (2) including external uncertainties, or (3) with propagated uncertainty from the correction standard (for methods A and B only). (A) NIST-610 as PRM and MDC as MCRM to calibrate $\mathrm{Rb}/\mathrm{Sr}$ ratios; (B) NIST-610 as PRM, Mica-Mg as MCRM to calibrate $\mathrm{Rb}/\mathrm{Sr}$ ratios; (C) $\mathrm{Rb}/\mathrm{Sr}$ ratios calibrated to Mica-Mg as PRM and $\mathrm{Sr}/\mathrm{Sr}$ ratios calibrated to NIST-610 as PRM; and (D) Mica-MG as PRM for both $\mathrm{Rb}/\mathrm{Sr}$ and $\mathrm{Sr}/\mathrm{Sr}$ ratios. MS is for mass spectrometry. MSWD is for mean squared weighted deviation.

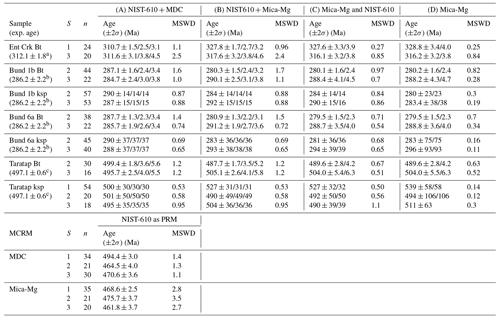
^a Rb–Sr TIMS age from Mortimer et al. (1987) and recalculated with the Villa et al. (2015) decay constant in IsoplotR (Vermeesch, 2018). The reported uncertainty is 95 % confidence interval but does not take overdispersion into account. ^b Zircon U–Pb age for the Banalasta Adamellite in the Bundarra Suite from Black (2007). ^c Zircon U–Pb TIMS age for the Taratap Granodiorite, as reported in Glorie et al. (2024).

Figure 4 compares the obtained Rb–Sr inverse isochron dates to the expected ages for the three samples that were analysed over two or three analytical sessions. The uncertainties for the K-feldspar dates are not shown, as they are too large to be useful (due to the relatively low-radiogenic nature of typical K-feldspar versus micas); here we only compare the accuracy of the absolute dates. As shown, analytical protocol (A) involving NIST-610 as PRM and MDC phlogopite as MCRM consistently gives the most accurate Rb–Sr dates across all different analytical sessions. For this analytical protocol, the Rb–Sr biotite dates for the Bundarra samples are 287.1 ± 2.4, 284.7 ± 3.0, 287.7 ± 2.3, and 285.7 ± 2.6 Ma (between two samples over two analytical sessions), which are in excellent agreement with the published zircon U–Pb age of 286.2 ± 2.2 Ma (Black, 2007) from the same outcrop. The K-feldspar dates of 290 ± 14, 285 ± 15, 290 ± 37, and 288 ± 37 Ma are in excellent agreement as well but are less useful to evaluate age accuracies, given their larger uncertainties. Similarly, for the Taratap sample, the obtained biotite Rb–Sr dates of 499.4 ± 3.6 and 495.7 ± 4.0 Ma, as well as the (imprecise) K-feldspar Rb–Sr dates of 500 ± 30, 501 ± 50, and 495 ± 35 Ma, are in excellent agreement with the zircon U–Pb ID-TIMS age of 497.1 ± 0.6 Ma and the apatite Lu–Hf age of 497.1 ± 5.5 Ma for the same sample (Glorie et al., 2024). Hence, the combined dataset suggests that the biotite, K-feldspar, and zircons record the same (crystallisation) age for both the Bundarra and Taratap samples. The Entire Creek biotite gave consistent Rb–Sr dates of 310.7 ± 1.5 and 311.6 ± 3.1 Ma, which are in excellent agreement with the ID-TIMS age of 312.1 ± 1.8/5.1 Ma (95 % confidence uncertainties, without/with overdispersion), based on the $\mathrm{Rb}/\mathrm{Sr}$ ratios in Mortimer et al. (1987) and recalculated with the Villa et al. (2015) Rb–Sr decay constant.

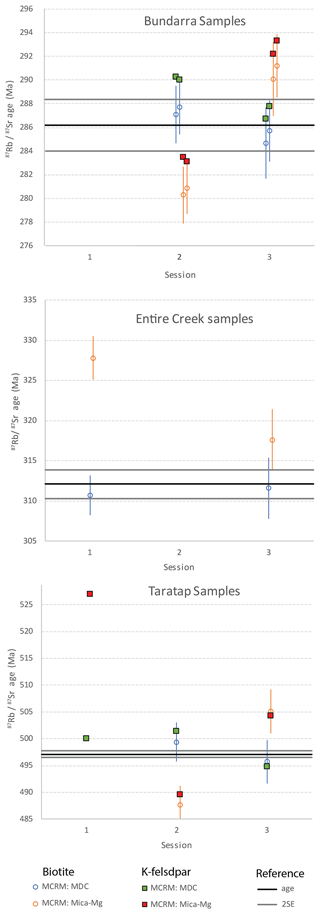
Figure 4 Comparisons of Rb–Sr dates over three analytical sessions, calibrated to either MDC or Mica-Mg as MCRM, with respect to the expected ages for each sample (black line with grey 2 SE uncertainty bars). In all cases, NIST-610 was used as PRM. Biotite data are plotted as open circles (blue is calibrated to MDC as MCRM; orange is calibrated to Mica-Mg as MCRM). K-feldspar data are plotted as filled squares (green is calibrated to MDC as MCRM; red is calibrated to Mica-Mg as MCRM).

5 Discussion

5.1 Downhole fractionation corrections

Few previous studies have reported Rb–Sr DHF trends for a series of artificial reference materials (i.e. glass standards and pressed pellets; Wang et al., 2022; Redaa et al., 2021). However, to the best of our knowledge, DHF trends have not been evaluated for natural materials, with the exception of phlogopite MDC (Redaa et al., 2021). In our experiments, DHF is more pronounced in natural micas and K-feldspar than observed for the NIST-610 glass and Mica-Mg pressed pellet when ablated under the same analytical conditions (Fig. 1). Comparatively, Mica-Mg appears least appropriate to correct the analysed samples for DHF, given its systematically different DHF trend. NIST-610 shows less DHF compared to the analysed micas and K-feldspars, but its trend is more systematic (similar shape with lower amplitudes). Thus, correcting for DHF against NIST-610 reduces the observed DHF for the analysed samples, while Mica-Mg significantly under-corrects for DHF or accentuates it when applied to minerals. MDC biotite would be the most appropriate choice for DHF correction, as it behaves in a very similar manner to the analysed mica and K-feldspar samples. However, as with most natural materials, MDC is not sufficiently homogenous in the ${}^{\mathrm{87}}\mathrm{Rb}{/}^{\mathrm{87}}\mathrm{Sr}$ ratio to be used as a PRM. While the shape or slope of DHF trends can vary, depending on laser conditions (spot size, frequency, and fluence), it cannot be eliminated for elements with contrasting volatilities such as Rb and Sr. However, based on the presented data, the use of NIST-610 is the more appropriate reference material to correct for DHF, and Mica-Mg would exacerbate instead of reduce the effects of DHF.

If no DHF correction is applied, accurate data can only be achieved if exactly the same signal interval is selected in both the RM and sample. If there is a residual DHF slope on the sample $\mathrm{Rb}/\mathrm{Sr}$ ratios that is different to the RM (e.g. crystalline material versus Mica-Mg), then selecting a shorter signal interval can significantly bias $\mathrm{Rb}/\mathrm{Sr}$ ratios and hence the apparent age.

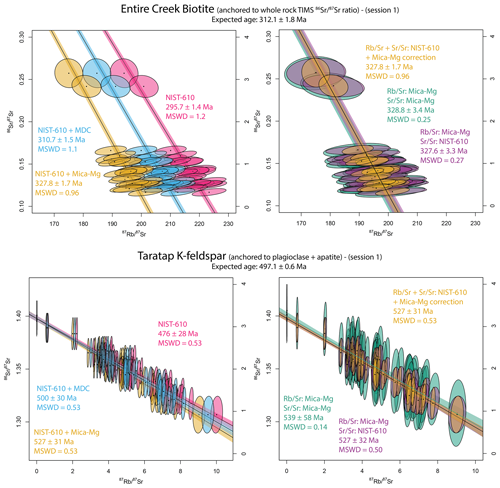
Figure 5 Comparisons of isochron dates obtained using the four different calibration protocols, using session 1 biotite Rb–Sr data from the Entire Creek sample and K-feldspar Rb–Sr data from the Taratap sample. Data plotted in red show NIST-610 as PRM without correction for matrix-induced fractionation. Data plotted in green show NIST-610 as PRM with Mica-Mg as MCRM. Data plotted in yellow show NIST-610 as PRM with MDC as MCRM. Data plotted in purple show NIST-610 as PRM for $\mathrm{Sr}/\mathrm{Sr}$ ratios and Mica-Mg as PRM for $\mathrm{Rb}/\mathrm{Sr}$ ratios. Data plotted in blue show both $\mathrm{Rb}/\mathrm{Sr}$ and $\mathrm{Sr}/\mathrm{Sr}$ ratios calibrated to Mica-Mg as PRM. The biotite data are highly radiogenic and show significant age differences, depending on the used MCRM. The K-feldspar data are low radiogenic, resulting in larger and overlapping uncertainties (refer to Fig. 3 for full isochron plots). Using NIST-610 as PRM produces the smallest uncertainties for individual data points.

5.2 Mica-Mg vs. NIST-610 and MDC as calibration standards

5.2.1 Uncertainty comparisons

The contributions to the propagated uncertainties about individual analyses from the reference materials (average signal precision and calibration curve misfit) are much larger when calibrating to Mica-Mg compared to NIST-610 for both ${}^{\mathrm{87}}\mathrm{Rb}{/}^{\mathrm{87}}\mathrm{Sr}$ and ${}^{\mathrm{86}}\mathrm{Sr}{/}^{\mathrm{87}}\mathrm{Sr}$ ratios (Fig. 5). For example, in analytical session 1, the obtained uncertainties for individual ${}^{\mathrm{87}}\mathrm{Rb}{/}^{\mathrm{87}}\mathrm{Sr}$ ratios for the Entire Creek biotite sample are more than double when using Mica-Mg compared to NIST-610 as the PRM (Fig. 5). As a result, the choice of Mica-Mg instead of NIST-610 as the PRM will increase the uncertainties about each analysis and might consequently mask the presence of multiple data populations. It will also introduces excessive uncertainties onto the calculated isochron dates.

The use of Mica-Mg as a calibration standard for ${}^{\mathrm{86}}\mathrm{Sr}{/}^{\mathrm{87}}\mathrm{Sr}$ ratios most significantly affects the isochron precision of low-radiogenic samples such as K-feldspar samples. As shown in Table 3 and Fig. 5, the uncertainty about the K-feldspar isochron dates can be up to 2× larger, when compared to other calibration methods. Furthermore, the resulting MSWD values on the isochron regressions are consistently <0.3 (Table 3), suggesting excessive uncertainties about individual data points. For the more radiogenic biotite samples, the larger uncertainties in ${}^{\mathrm{86}}\mathrm{Sr}{/}^{\mathrm{87}}\mathrm{Sr}$ ratios have negligible effects to the precision on the isochron dates.

The precision of the calibrated ${}^{\mathrm{87}}\mathrm{Rb}{/}^{\mathrm{87}}\mathrm{Sr}$ ratios is more important to the isochron uncertainty about highly radiogenic materials, such as most types of micas. Calibrating to NIST-610 versus Mica-Mg yields either more precise biotite isochron dates or identical precision. However, when NIST-610 is used as the PRM, uncertainty propagation from the MCRM (MDC or Mica-Mg) leads to either identical or slightly worse isochron uncertainties when compared to using Mica-Mg as PRM (Fig. 5; Table 3). The difference relates to the degree of overdispersion. The larger uncertainties about the $\mathrm{Rb}/\mathrm{Sr}$ ratios when using Mica-Mg as PRM result in lower MSWD values, reducing the uncertainty of the isochron regression. This excess uncertainty, when calibrating to Mica-Mg, might mask meaningful geological scatter in $\mathrm{Rb}/\mathrm{Sr}$ ratios, and it is, therefore, advisable to produce isochrons based on data with the best possible analytical precision.

In summary, Mica-Mg should not be used as calibration standard for ${}^{\mathrm{86}}\mathrm{Sr}{/}^{\mathrm{87}}\mathrm{Sr}$ ratio calculations for low-radiogenic samples, as it introduces excessive uncertainties to age calculations. For high-radiogenic samples, using Mica-Mg as the PRM also introduces larger uncertainties to individual data points compared to using NIST-610, but there is no significant difference in propagated uncertainty after secondary correction to either MDC or Mica-Mg. For $\mathrm{Rb}/\mathrm{Sr}$ ratio calibrations, NIST-610 is more consistent, resulting in lower uncertainties for individual $\mathrm{Rb}/\mathrm{Sr}$ ratios. When there is no overdispersion, this results in better isochron age precision. However, overdispersion can be masked by the increased uncertainties for $\mathrm{Rb}/\mathrm{Sr}$ ratios, resulting in better apparent precision when data are calibrated to Mica-Mg.

5.2.2 Accuracy comparisons

It has been observed previously that Rb–Sr dates are offset from their expected ages when calibrated to the NIST-610 reference material (e.g. Wang et al., 2022; Gorojovsky and Alard, 2020). In contrast, Mica-Mg seems to better reproduce expected ages, although the significant uncertainties obtained for natural materials in previous studies render appropriate accuracy testing difficult. For example, Wang et al. (2022) compare measured to expected Rb–Sr dates for three samples with known ages. The best achieved uncertainty in their experiment was ∼ 2.6 % for one sample, while for the other samples the reported uncertainties are ∼ 5.6 % and 6.3 %. Similarly, the accuracy comparisons in Gorojovsky and Alard (2020) use the Monastery phlogopite, with a precision of ∼ 4 % when calibrated to Mica-Mg. Both papers report data normalised to NIST-610 but do not apply a secondary correction for matrix-dependent fractionation.

For the biotites analysed in our study, the fully propagated 95 % confidence interval uncertainties ranges between 0.8 % and 1.6 % when calibrated to Mica-Mg and between 1.0 % and 1.4 % when calibrated to NIST-610 and corrected to MDC (depending on the sample and analytical session; Table 3), allowing for more detailed accuracy comparisons. Figure 4 illustrates that using NIST-610 and MDC as calibration reference materials produces the most accurate results, compared to the expected references dates. For the biotite results, the obtained Rb–Sr dates are within 0.5 % accuracy when compared to the expected ages. The K-feldspar dates are accurate within 1 %, except for session 2, where accuracy is within 1.5 %. When the same data are calibrated against Mica-Mg (either using NIST-610 as the PRM and Mica-Mg as MCRM or directly using Mica-Mg as the PRM), the results are significantly offset from their expected ages. For the biotite results calibrated to Mica-Mg, accuracy is within 2 % for sessions 2 and 3, and there is 5 % age offset in session 1. For the K-feldspars, the age offset is up to 2.5 % in sessions 2 and 3 and 6 % in session 1. While the age offsets in sessions 2 and 3 might be regarded as “acceptable”, given the obtained precision, the more significant inaccuracy in session 1 renders Mica-Mg to be less desirable as a PRM.

The difference in accuracy between session 1 and sessions 2 and 3 can be explained by the difference in measured dates for the MDC and Mica-Mg reference materials normalised to NIST-610. For sessions 2 and 3, MDC and Mica-Mg produced similar isochron dates (2.3 % and 1.9 % difference, respectively) (Table 3; Fig. 6). For session 1, however, MDC gives a significantly different age (494 ± 4 Ma) compared to Mica-Mg (469 ± 4 Ma). These differences in accuracy (ca. 5 % in session 1 and ca. 2 % in sessions 2 and 3) are in line with the observed age offsets between the measured dates and reference dates for the biotite and K-feldspar samples calibrated to Mica-Mg.

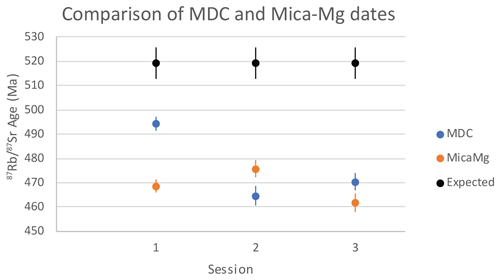
Figure 6 Rb–Sr dates for MDC and Mica-Mg calibrated to NIST-610 over the three analytical sessions used in this paper. The offset of the Rb–Sr age with respect to the reference age is used to calculate the correction factor on the $\mathrm{Rb}/\mathrm{Sr}$ ratios. Uncertainties are 2 SE.

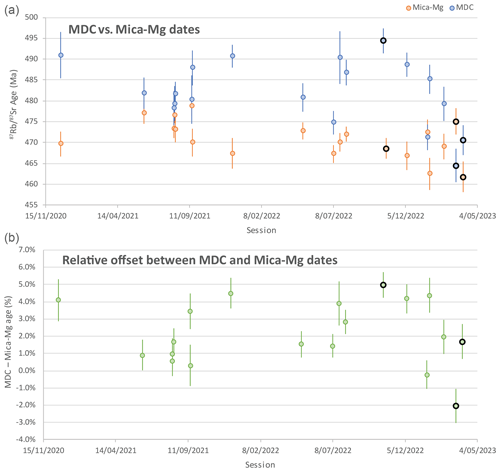
Figure 7 Long-term (2.5 years) Rb–Sr age data for Mica-Mg and MDC for the lab (Adelaide Microscopy). All uncertainties are 2 SE. Panel (a) shows absolute dates, and panel (b) shows the percentage difference between the MDC and Mica-Mg dates. All data were processed in the same way, using NIST-610 as PRM. The three analytical sessions previously discussed are highlighted by black rims and capture the most extreme differences obtained in our lab to date. Given that MDC as MCRM produces consistently accurate data, the plot indicates that Mica-Mg as PRM can lead to up to 5 % inaccuracy in Rb–Sr age calculations.

5.2.3 Long-term comparison between MDC and Mica-Mg as secondary calibration standards

Given that the accuracy of the Rb–Sr method appears to be significantly dependent on the applied calibration reference materials and that the measured Rb–Sr dates of these calibration standards fluctuate significantly between analytical sessions when compared to NIST-610, the long-term behaviour of the MDC and Mica-Mg reference materials needs to be evaluated. Figure 7 presents 2.5 years of measured Rb–Sr dates for MDC and Mica-Mg, both calibrated to NIST-610 as the PRM. All data in this plot have been processed identically. The Rb–Sr dates for Mica-Mg are generally more consistent, ranging between ca. 462 and 479 Ma, with a standard deviation of 4.5 Ma, while the MDC dates show more variation, ranging between ca. 465 and 494 Ma, with a standard deviation of 7.7 Ma. In all but two sessions, MDC produces an older Rb–Sr date compared to Mica-Mg. The analytical sessions discussed above are highlighted in Fig. 7 and encompass the maximum variability in measured Rb–Sr dates for MDC. With the premise that calibration to NIST-610 and MDC produces accurate Rb–Sr dates (as discussed in Sect. 5.2.2), the difference between the measured MDC and Mica-Mg dates (Figs. 6, 7) can be regarded as an estimate of the degree of inaccuracy when data are calibrated to Mica-Mg. While some sessions reveal very little offset between both standards, using Mica-Mg as calibration standard can lead to up to 5 % inaccuracy in Rb–Sr dates. The cause of the observed variability is currently unknown; however, in the second-to-last session with a significantly older Mica-Mg date compared to MDC, the analysed samples might have received a lower effective laser fluence compared to other sessions, as the glass between the laser beam and samples was not cleaned prior to analysis. The lower fluence could change the effective matrix bias between NIST-610, Mica-Mg, and MDC; however, calibration of biotite against MDC produces accurate results, as demonstrated in Sect. 5.2.2. In contrast, although Mica-Mg produces more consistent Rb–Sr dates between analytical sessions, these dates are unreliable, given the variable and unsystematic degree of inaccuracy between sessions.

6 Conclusions

Based on our observations, the use of Mica-Mg as calibration reference material is not recommended for the following reasons:

1. The downhole fractionation (DHF) trend for Mica-Mg is not comparable with the DHF trends of natural biotite, phlogopite, and K-feldspar (Fig. 1). Using Mica-Mg to correct DHF would exacerbate instead of reduce DHF in those minerals.

2. Given the relatively poor reproducibility of ${}^{\mathrm{87}}\mathrm{Rb}{/}^{\mathrm{87}}\mathrm{Sr}$ ratios and significant uncertainty about individual ${}^{\mathrm{87}}\mathrm{Sr}{/}^{\mathrm{86}}\mathrm{Sr}$ measurements (Fig. 2), Mica-Mg as PRM or MCRM introduces excess uncertainty that can be avoided when using a more consistent PRM such as NIST-610.

3. We demonstrated that calibrating to Mica-Mg may lead to up to 5 % inaccuracy in Rb–Sr age (Figs. 4, 6, 7) and that the degree of inaccuracy is unsystematically session dependent.

We suggest a different approach involving the (1) calibration of the ${}^{\mathrm{87}}\mathrm{Rb}{/}^{\mathrm{87}}\mathrm{Sr}$ and ${}^{\mathrm{87}}\mathrm{Sr}{/}^{\mathrm{86}}\mathrm{Sr}$ ratios to a primary reference material with high Rb and Sr concentrations and homogenous isotopic ratios such as NIST-610 glass, including DHF correction of the $\mathrm{Rb}/\mathrm{Sr}$ ratios, followed by (2) a correction of the ${}^{\mathrm{87}}\mathrm{Rb}{/}^{\mathrm{87}}\mathrm{Sr}$ ratio to a natural mineral MCRM with a similar DHF trend to the samples to be analysed. In our observations with a 67 µm spot size, there are no significant differences in the matrix effects comparing biotite, phlogopite, and K-feldspar, suggesting that any of these natural minerals as MCRM can produce accurate dates for K-rich minerals. We have used MDC phlogopite as MCRM and demonstrate accurate Rb–Sr dates for a range of biotites and K-feldspars with well-established age constraints. For the biotite dates, the fully propagated uncertainties are <1.5 %, allowing accuracy verifications at high analytical precision. The K-feldspar dates have relative high uncertainties (ca. 5 %–10 %), and therefore, the accuracy of the calibration cannot be robustly tested. However, absolute values agree with biotite dates, and for a given sample, biotite and K-feldspar analyses statistically constitute a single isochron.

Finally, while this two-step calibration protocol is currently recommended due to current constraints with data-processing software, new developments involving calibrating to isochronous reference materials might become the desired approach in the future.