Interlaboratory reproducibility of ID-TIMS U–Pb geochronology evaluated with a pre-spiked natural zircon solution

The highest precision and accuracy in U–Pb geochronology is achieved using isotope dilution thermal ionisation mass spectrometry (ID-TIMS), a technique which owes its reliability to precise Pb and U isotope ratio analysis, a largely unified framework of lab protocols, and common isotopic tracers with accurately determined compositions. However, while hardware and protocol developments have steadily improved the analytical precision, the level to which ID-TIMS U–Pb dates from different laboratories agree remains largely unquantified. To better assess both internal repeatability and interlaboratory reproducibility of this method, we have conducted an experiment in which a large batch of natural zircon was dissolved, mixed with a newly prepared ²⁰⁵Pb–²³³U–²³⁵U tracer, and distributed as solution to participating laboratories. Thus prepared, pre-spiked, homogeneous PLES535 solution underwent the full sample preparation and analysis process separately in each lab, allowing a maximally unbiased comparison of the entire analytical procedure on a sample of unknown age. The results from 14 instruments at 11 institutions demonstrate internal repeatability of individual labs at 5 to 10 U–Pb analyses, with mean squared weighted deviation (MSWD) values generally indicative of single age populations. Lab weighted-mean ²⁰⁶Pb $/$ ²³⁸U and ²⁰⁷Pb $/$ ²³⁵U ages for the 337 Ma zircon solution agree within 0.05 % and 0.09 % (2 standard deviations), respectively. This underscores the reliability of the participating laboratories for precise and accurate zircon U–Pb analyses, while highlighting the need for continued exchange on lab protocols and method improvement. We identify likely reasons for the remaining interlaboratory bias and discuss ways forward toward the goal of 0.01 % reproducibility.

1 Introduction

U–Pb geochronology is used to date common U-bearing minerals such as zircon employing a variety of analytical methods, ranging from spatially resolved, low-precision microbeam techniques to high-precision approaches requiring the dissolution of the dated mineral (e.g. Schoene, 2014). The technique of choice for the highest-precision U–Pb age determination is isotope dilution thermal ionisation mass spectrometry (ID-TIMS), where single crystals or crystal fragments are dissolved in acid, homogenised with an enriched isotope tracer, purified to isolate the elements U and Pb, and subsequently analysed for isotopic composition by high-precision mass spectrometry. This approach boasts the status of the “gold standard” of geochronology because of its unparalleled precision, accuracy, and traceability (Schaltegger et al., 2024). This position is an effect of several decades of coordinated efforts of the ID-TIMS U–Pb geochronology community, particularly since the inception of the EARTHTIME initiative which introduced common tracer and standard solutions, lab best practices, data reduction schemes, and software (Bowring et al., 2005; Schmitz and Schoene, 2007; Bowring et al., 2011; McLean et al., 2011; Condon et al., 2015; McLean et al., 2015; Schaltegger et al., 2021; Condon et al., 2024). Initial goals of EARTHTIME stated the target of reaching an analytical precision and interlaboratory reproducibility of 0.1 % or better. Today, as lab preparation becomes cleaner and mass spectrometer analyses more precise, the target has shifted to an order-of-magnitude improvement upon the original goals. In optimal conditions, ID-TIMS can achieve internal precision of < 0.02 % on single U–Pb dates and surpass 0.01 % on weighted mean uncertainties (n > 5; e.g. Wotzlaw et al., 2017; Szymanowski and Schoene, 2020). This precision level is taken full advantage of when comparing ages from a single lab using a single tracer solution and avoiding any potential interlaboratory biases. This is particularly important when creating detailed stratigraphic age models based on geochronology of intercalated ash beds, where not propagating such systematic sources of uncertainty may be key to the ultimate temporal resolution (e.g. Metcalfe et al., 2015; Sahy et al., 2015; Baresel et al., 2017; Bruck et al., 2023).

Internal repeatability of ID-TIMS labs is often demonstrated by repeated analyses of zircon reference materials, unknowns with little age dispersion, or synthetic solutions, but it remains unclear how well these U–Pb dates compare between labs. Early comparison exercises of the EARTHTIME initiative were frustrated by the heterogeneity of natural zircon populations (e.g. due to Pb loss), uncertainties in tracer composition, and variations in pre-treatment techniques or blank contribution between labs (Condon and EARTHTIME U–Pb Working Group, 2005). No other community-wide initiatives have been attempted since then, largely due to the lack of appropriate materials that would allow for a rigorous test. First-order comparisons of lab performance have been offered by studies characterising natural zircon crystals tested as potential microanalytical reference materials; such studies have typically involved two to five laboratories dating zircon crystals separated from the same rock sample (Sláma et al., 2008; Eddy et al., 2019) or fragments of large zircon megacrysts (Wiedenbeck et al., 1995; Nasdala et al., 2008; Kennedy et al., 2014; Nasdala et al., 2018). Unfortunately, close inspection of some common multi-crystal reference zircons reveals grain-to-grain heterogeneity at the per mil level (Widmann et al., 2019; Schaltegger et al., 2021), which far exceeds modern analytical precision in ID-TIMS and makes them unsuitable for the purpose of assessing interlaboratory reproducibility. Analysing zircon megacrysts, on the other hand, relies on their internal age homogeneity, which adds a layer of uncertainty to such exercises.

An alternative approach to interlaboratory comparison uses synthetic U–Pb solutions such as those prepared by Condon et al. (2008) and Connelly and Condon (2014) with isotopic compositions corresponding to apparent U–Pb dates of 100, 500, 2000, and 4567 Ma. These “ET solutions” are variably analysed by ID-TIMS labs and occasionally included in publications as a quality check, but known issues of repeatability have so far prevented them from becoming accepted community standards (Schaltegger et al., 2021). Recently, Schaltegger et al. (2021) presented double-spiked ET100 and ET2000 data from three labs, demonstrating some excess scatter in ET100 ²⁰⁶Pb $/$ ²³⁸U dates (mean squared weighted deviation (MSWD) = 2.6, n = 67, spread of three lab weighted means of 0.025 %) and a good level of agreement of ET2000 ²⁰⁷Pb $/$ ²⁰⁶Pb dates (MSWD = 1, n = 59). While the ET solutions are homogeneous, they are unspiked and therefore require tracer to be added prior to analysis – this is convenient in day-to-day use, but it has been suggested that Pb–U fractionation prior to sample–tracer equilibration can be responsible for some of the excess variance in U–Pb dates (Schaltegger et al., 2021). Furthermore, the synthetic ET solutions do not contain any zircon matrix and therefore do not require chromatographic separation of U and Pb from other elements. While again convenient in routine use, this deviates from lab protocols for natural zircon and results in very clean U–Pb loads that may behave differently during thermal ionisation mass spectrometry (e.g. mass bias, isobaric interferences, ionisation efficiency) from U–Pb fractions separated from natural zircon crystals.

This paper summarises the results of a study designed to address intra- and interlaboratory reproducibility in a way that avoids the pitfalls of natural zircon heterogeneity, differences in the spike (tracer) used by the different labs, or issues with sample–tracer equilibration, all while maintaining a natural zircon matrix in a homogeneous solution. Through community input during a U–Pb ID-TIMS workshop held in 2018, an experiment was designed and carried out that involved producing a large batch of homogeneous, pre-spiked zircon solution “PLES535”, which was then distributed to 15 ID-TIMS laboratories for analysis. By working with a natural zircon solution and avoiding local tracer addition, we have limited the scope of our test to the final preparation steps and thermal ionisation mass spectrometry analyses. The results of this experiment offer a critical evaluation of internal repeatability and interlaboratory reproducibility of Pb and U isotopic ratios and U–Pb zircon dates that involves much of the active ID-TIMS geochronology community. Differences in U–Pb dates beyond the reproducibility reported here can thus be confidently interpreted as real, “geologic” differences.

2 Materials and methods

2.1 Experimental setup

Following community input, the reproducibility experiment was designed to include two phases.

1. The PLES535 solution was first prepared by batch acid dissolution of milligram amounts of chemically abraded natural zircon, after which it was equilibrated with a U–Pb spike of known composition. The solution was then distributed in liquid form to individual labs together with information about the received aliquot and detailed instructions about final sample preparation and analysis.

2. At the participating labs, PLES535 solution was purified to isolate U and Pb from a predefined sample amount which was optimal for the goals of the experiment, and the U–Pb isotopic ratios were analysed following each lab's methods as applied to routine zircon analyses.

Below we provide details of all preparatory and analytical steps.

2.2 Plešovice zircon

The chosen natural material was a monomineralic zircon separate retrieved by standard mineral separation techniques from a potassic granulite from Plešovice, southern Bohemian Massif, Czechia (Sláma et al., 2008), widely used as a reference material (RM) for bulk and in situ U-Pb and Hf isotope analysis. Individual zircon grains reach millimetre to centimetre size and are commonly characterised by internal oscillatory and sector zoning, variable U contents of 400–3000 ppm, and a consequent heterogeneity in the amount of accumulated radiation damage. The existing reference age for Plešovice zircon was obtained by pooling single-crystal chemical abrasion (CA)-ID-TIMS results from four labs using the EARTHTIME ²⁰⁵Pb–²³³U–²³⁵U spike, yielding a weighted mean ²⁰⁶Pb $/$ ²³⁸U age of 337.13 ± 0.37 Ma (Sláma et al., 2008); however, significant age heterogeneity among crystals of Plešovice zircon is apparent in the results of Widmann et al. (2019). Note that the purpose of this experiment is not to reproduce or improve that result but to produce a sufficient amount of homogeneous natural zircon solution of the right compositional characteristics.

2.3 ETH-535 spike

The limited availability of ²⁰²Pb precluded the use of a ²⁰²Pb–²⁰⁵Pb spike for this study, so a new ²⁰⁵Pb–²³³U–²³⁵U spike was mixed at ETH Zurich. The lack of a pair of Pb isotopes with a known ratio in the analyses limits the precision of the correction for mass fractionation in the mass spectrometers and is the largest single source of uncertainty in derived dates. Only with new production of high-purity ²⁰²Pb, or a significant consumption of remaining ²⁰²Pb–²⁰⁵Pb spikes, will higher precision inter-lab comparisons be possible. The spike (“ETH-535”) was prepared from an aliquot of high-purity ²⁰⁵Pb solution with ²⁰⁵Pb $/$ ²⁰⁴Pb ∼ 3000 and ²⁰⁵Pb concentration of 0.92 ng g⁻¹. This ²⁰⁵Pb solution was mixed with a ²³³U–²³⁵U double spike targeting ²³⁵U $/$ ²⁰⁵Pb of 45. The resulting ²³⁵U $/$ ²⁰⁵Pb ratio was calibrated against the ET100 synthetic solution (Condon et al., 2008), assuming a ²⁰⁶Pb $/$ ²³⁸U date of 100.173 Ma and yielding a ²³⁵U $/$ ²⁰⁵Pb ratio of 45.298. This provides an indirect calibration relative to the EARTHTIME tracer solution used by Schaltegger et al. (2021). This approach to tracer calibration is not meant to be rigorous, nor does it need to be: since all participating labs used the exact same solution and spike calibration, any inaccuracy in the spike calibration should not affect the interlaboratory comparison.

2.4 Preparation of PLES535 solution

At the University of Geneva, a total of 20.3 mg of Plešovice crystals was combined in a quartz crucible and annealed in a muffle furnace for 48 h at 900 °C. The mineral separate was then partially dissolved in 29 M HF (“chemically abraded”, Mattinson, 2005) in a clean 3 mL PFA vial held inside a Parr dissolution vessel kept at 210 °C for 12 h. The chemically abraded mineral separate was then repeatedly rinsed in water and HNO₃ and aliquoted into 30 individual 200 µL PFA microcapsules, which were filled with 29 M HF and a drop of HNO₃ and assembled inside two Parr vessels for complete dissolution achieved over > 60 h at 210 °C. The resulting solutions were dried down, redissolved in 6 M HCl at 180 °C in the oven, and again dried down to chloride salts. Finally, all aliquots were brought up in 6 M HCl and combined in a 7 mL PFA vial to yield 1.7 mL of solution.

At ETH Zurich, the homogenised Plešovice zircon solution was combined with ETH-535 in a clean PFA dropper bottle (mother bottle numbered 0) to yield target ratios of ²⁰⁶Pb $/$ ²⁰⁵Pb = 5 and ²³⁸U $/$ ²³⁵U = 2, optimised for balance between spike availability, number of participating labs, proposed aliquot size and the consequent importance of blank correction, and the optimal dynamic range of used detectors. The mixture was refluxed for 24 h on a hotplate to equilibrate the spike and sample. Twenty 1.5 mL aliquots of the solution were transferred into virgin pre-cleaned 3 mL PFA vials using a pipette with pre-cleaned tips, numbered 1–20, and prepared for distribution. The total mass of each aliquot (solution + vial) was determined to allow solution loss to be assessed (e.g. by evaporation or leakage) during transport. The handling did not introduce significant Pb contamination, which was < 0.1 pg Pb${}_{\mathrm{c}}/\mathrm{50}$ µL, as measured in both the mother bottle and the distributed aliquots.

2.5 Preparation at participating labs

The participating labs were asked to return U–Pb isotopic ratios from 10 aliquots per instrument, with the size of the aliquot (50 µL) corresponding to ca. 80 pg radiogenic Pb (Pb^*) and 1.6 ng sample U and thus insensitive to typical blank corrections. Aliquot processing was designed to approximate routine single-crystal zircon sample preparation; i.e. 50 µL of solution per aliquot was pipetted from the distributed vials into PFA microcapsules, dried down, and redissolved in 6 M HCl in a dissolution vessel held in a > 180 °C oven. After drying, the samples were brought up in 3 M HCl and loaded into 50 µL microcolumns filled with AG1-X8 resin (200–400 mesh, chloride form) to isolate U and Pb in an ion exchange chromatography procedure modified from Krogh (1973). Lab 14 had issues with clean air supply, so to reduce exposure, their aliquots were directly dried down in beakers without ion exchange. All combined U–Pb fractions were dried down with a microdrop of dilute (0.02–0.05 M) H₃PO₄ and subsequently loaded in a silica gel emitter (recipes variably modified from Gerstenberger and Haase, 1997) onto degassed, zone-refined Re filaments for TIMS analysis.

2.6 Mass spectrometry and data reduction

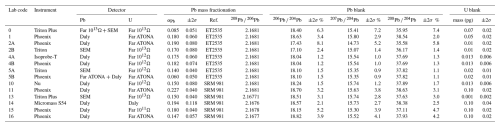
The choice of the TIMS analytical setup (used detectors, ionisation temperature, number of analytical cycles, etc.) was left to the participating labs. Overall, three instrument lineages/manufacturers were represented among the 11 labs that returned data: VG/Micromass/GV/Isotopx (n=9), Thermo Scientific (n=4), and Nu Instruments (n=1). Three labs provided data from two instruments; of those, lab 4 had two Isotopx instruments, and labs 2 and 5 each had a Thermo and an Isotopx instrument. Various detector combinations were used, with the biggest variability seen in the methods of analysing Pb isotopes. All relevant systematic lab- and detector-specific data are summarised in Table 1.

Table 1 Summary of instrumental setups and constants used.

Most labs analysed all included Pb isotopes (^204–208Pb) in peak-hopping mode on an ion-counting system, either a Daly/photomultiplier detector or a discrete-dynode secondary electron multiplier (SEM), with the dead time calibration and baseline settings of each left to the decision of the participants. Lab 0 analysed Pb isotopes in static mode on Faraday cups connected to 10¹³Ω amplifiers for ^205–208Pb, and axial SEM for ²⁰⁴Pb. In this case, the relationship between intensities on Faraday cups and the SEM (“yield”) was calibrated daily with an automated routine run on a Pb beam of ca. 12 mV. The Faraday baseline was determined off-peak, twice daily, for 1 h. Lab 5B used Faraday cups connected to the ATONA capacitive transimpedance amplifiers for ^205–208Pb and an axial Daly detector for ²⁰⁴Pb following the methods of Szymanowski and Schoene (2020). Mass fractionation during Pb isotopic analyses is instrument- and detector-specific and was corrected for by every lab with their best estimate of α_Pb (a linear Pb fractionation factor) derived from a compilation of Pb isotopic analyses, either of double-spiked samples or of Pb isotopic standard reference materials (Table 1). Corrections for Pb procedural blanks were made by assuming that all ²⁰⁴Pb was introduced as contamination at participating labs, with the blank composition estimated by each lab based on own measurements of total procedural blanks (Table 1).

Uranium was analysed as dioxide, collecting ²⁶⁵(UO₂), ²⁶⁷(UO₂), and ²⁷⁰(UO₂) in Faraday cups connected to either resistor-based amplifiers (10¹¹Ω, 10¹²Ω, or 10¹³Ω) or the ATONA amplifiers, with variable approaches to baseline correction. Only at lab 14 were U analyses conducted using a Daly/photomultiplier system. Analysing U as dioxide requires a correction for interferences of ¹⁸O-substituted ²³³UO₂ on ²³⁵UO₂, which was done either by assuming a constant ¹⁸O $/$ ¹⁶O value or using in-run corrections derived from analysing ²⁷²(UO₂) or ²⁶⁹(UO₂) (Condon et al., 2015; Wotzlaw et al., 2017; Szymanowski and Schoene, 2020). Instrumental mass fractionation was corrected offline using mean measured ratios and the known spike composition, while the sample was assumed to have ²³⁸U $/$ ²³⁵U = 137.818 ± 0.045 (Hiess et al., 2012). Procedural blank U was assumed to have the same isotopic composition as the zircon solution, while its mass was estimated independently by each lab (Table 1).

Data reduction was done according to each lab's preferences. Most labs used the Tripoli and ET_Redux software (Bowring et al., 2011) which follow the algorithm of McLean et al. (2011). Labs 4 and 10 used the UPbR spreadsheet based on the equations of Schmitz and Schoene (2007). Lab 14 used the PbMacDat spreadsheet based on Ludwig (1980, 1988) corrected for the original mistake in ²⁰⁶Pb $/$ ²³⁸U error assessment and updated to the Hiess et al. (2012) ²³⁸U $/$ ²³⁵U value. U–Pb dates were calculated using the decay constants of Jaffey et al. (1971), and no corrections for Th or Pa disequilibrium were applied. The composition of the ETH-535 spike was provided to the participating labs and thus kept constant. As such, the main differences in the analytical protocol and data reduction were limited to clean lab preparation and mass spectrometry: detector calibration, α_Pb, Pb blank isotopic composition, U blank mass and isotopic composition, and UO₂ oxide interference correction.

3 Results

Out of 15 laboratories that agreed to participate in the experiment, 11 returned full (10 analyses) or partial datasets, which are anonymised and marked with “lab code” throughout (Table 1). Three labs provided results from two mass spectrometers; those are denoted as A and B. The compiled data include raw uncorrected isotope ratios; fully reduced U–Pb dates (Fig. 1, Table 2); and a variety of systematic, lab- or instrument-specific values used in data reduction (all data available in Table S1 in the Supplement). This offered an opportunity to not only compare the reported U–Pb dates but also scrutinise the individual Pb and U isotopic ratio components used in deriving those dates to provide meaningful assessments of lab performance.

Figure 1 Wetherill concordia diagram of all PLES535 results in the experiment.

Table 2 Weighted mean ages obtained by each lab.

^* Uncertainties expanded to include overdispersion following Vermeesch (2018).

3.1 Lead isotopic ratios

PLES535 was prepared with a ²⁰⁵Pb (“single-Pb”) spike, which requires that every analysis be corrected externally for Pb mass fractionation with a specific fractionation factor (α_Pb, Table 1). Abundant Pb (25–88 pg Pb^*) permitted high-precision isotopic analyses, so not only was this correction critical for the accuracy of the Pb isotopic ratios and the resulting U–Pb dates, but it also largely determined their final precision. Indeed, the uncertainty assigned to α_Pb in each dataset typically dominated the uncertainty budget of calculated U–Pb dates, exceeding 90 % of the variance in some of the most precisely analysed aliquots.

Before mass fractionation correction, the reported raw measurement precision (2σ) for major Pb isotopic ratios ranged over an order of magnitude: 0.005–0.04 % for ²⁰⁶Pb $/$ ²⁰⁵Pb, 0.012–0.09 % for ²⁰⁷Pb $/$ ²⁰⁵Pb, 0.015–0.33 % for ²⁰⁸Pb $/$ ²⁰⁵Pb, and 0.18–1.5 % for ²⁰⁶Pb $/$ ²⁰⁴Pb, scaling with the relative abundance of the analysed isotopes (Fig. 2). Datasets where Pb isotopes were collected with Faraday-based detection systems (ATONA or 10¹³Ω amplifiers) exhibit substantially better precision of raw ratios compared to data acquired with ion counters (Daly or SEM); e.g. for ²⁰⁶Pb $/$ ²⁰⁵Pb, uncertainties on most Faraday data were better than 0.01 %, while for ion counter data they were mostly 0.01 %–0.04 %. Within the range of data acquired on ion counters, there are large and systematic differences in raw ratio precision among labs (Fig. 3). Given comparable hardware, this suggests systematic differences in terms of Pb ionisation efficiency, evaporation rate, or acquisition time. Run temperature and acquisition time were chosen by the analysts based on the available intensity and target precision; however, the relative importance of all the factors on final analytical precision is difficult to assess with the available data. It is also worth noting that, unless specifically corrected, Pb isotopic data measured by peak hopping on an ion counter may have underestimated uncertainties due to cycle-to-cycle correlations induced by beam interpolation algorithms (Ludwig, 2009). We also note large differences in the precision of ²⁰⁸Pb determination, which reflects reduced ²⁰⁸Pb counting times preferred by some labs.

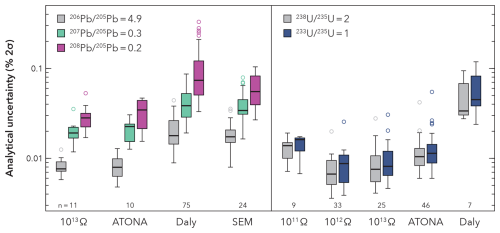
Figure 2 Summary of analytical precision achieved for uncorrected Pb and U isotope ratios using different detector types. Faraday detectors are divided by amplifier type and resistance: traditional 10¹¹Ω, 10¹²Ω, and 10¹³Ω amplifiers and the capacitive transimpedance amplifiers ATONA. Ion-counting systems include secondary electron multipliers (SEMs) and Daly/photomultiplier systems.

Once the detector-specific fractionation correction and aliquot-specific Pb blank correction are applied and the corresponding uncertainties are propagated, the measured Pb isotopic ratios of PLES535 can be assessed for internal and interlaboratory reproducibility (Fig. 4a). Taking ²⁰⁶Pb $/$ ²⁰⁵Pb as an example which is least limited by count rates, the results agree within 0.09 % (2 standard deviations of lab weighted means). However, about half of the datasets are characterised by internal scatter in excess of that expected from a homogeneous population. A few datasets (no. 10, 11, 13) display increased scatter, with outliers predominantly to lower ²⁰⁶Pb $/$ ²⁰⁵Pb (lower sample/spike).

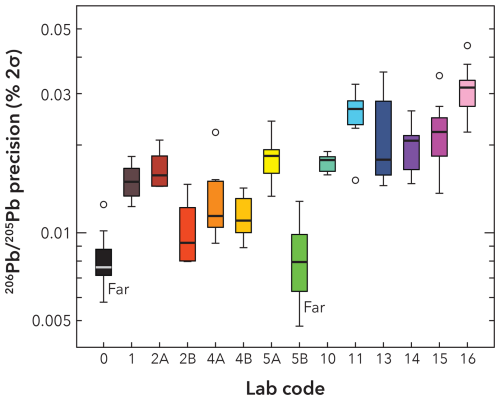
Figure 3 Precision of the uncorrected ²⁰⁶Pb $/$ ²⁰⁵Pb ratio by lab code. Labs 0 and 5B used Faraday detectors to analyse Pb isotopes, all others used ion counters.

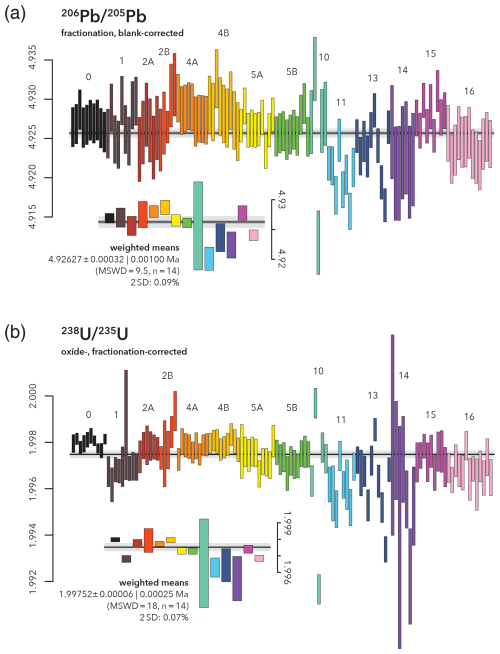
Figure 4 Reproducibility of key Pb (a) and U (b) isotope ratios analysed in PLES535. Raw ²⁰⁶Pb $/$ ²⁰⁵Pb ratios were corrected for mass fractionation and lab blank (Table 1). ²³⁸U $/$ ²³⁵U ratios were corrected for oxide interferences (done by each lab individually) and mass fractionation, assuming zircon ²³⁸U $/$ ²³⁵U = 137.818 of Hiess et al. (2012). All data are reported with 2σ uncertainty represented as bar height. Uncertainty on weighted means is given in the form $\pm x|y$, where x represents the weighted mean uncertainty, and y additionally includes overdispersion in cases of excess scatter (e.g. Vermeesch, 2018).

3.2 Uranium isotopic ratios

Uranium isotope ratio analyses of PLES535 benefitted from the ²³³U–²³⁵U double spike, which allowed a mass fractionation correction using ratio means and assuming a sample ²³⁸U $/$ ²³⁵U, without the need to independently estimate α_U. The only free parameter in U data reduction remained the mass of U blank, with the blank isotopic composition assumed identical to that of zircon.

Uranium isotopes were generally analysed with Faraday detectors, achieving a common level of precision for U isotope ratios between 0.004 %–0.02 %, largely independent of the used instrument and amplifier type; only analyses utilising 10¹¹Ω amplifiers were less precise than most other Faraday setups at 0.01 %–0.02 %. One dataset was produced using a Daly system and has a reduced precision of 0.03 %–0.09 % (Fig. 2).

The fractionation-corrected ²³⁸U $/$ ²³⁵U ratios before blank correction agree within 0.07 % (2 standard deviations of lab weighted means), but, like Pb, about half of the single-lab datasets show excess scatter (Fig. 4b). Similar to Pb isotopes, datasets 10, 11, 13, and 14 show extra scatter with outliers predominantly to lower ²³⁸U $/$ ²³⁵U (lower sample/spike). This suggests unresolved issues with mass spectrometry data acquisition or variable, non-systematic contributions of U lab contamination.

3.3 U–Pb dates

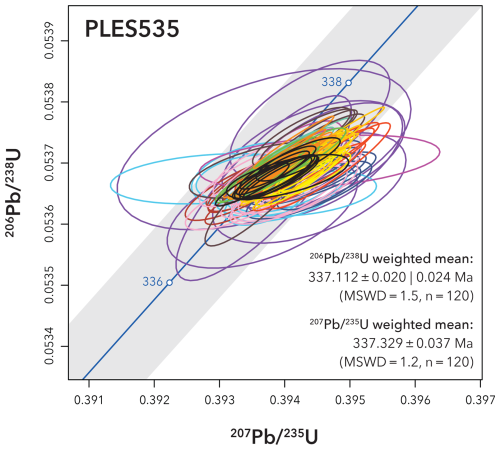
Combining the Pb and U isotopic ratios into U–Pb dates for PLES535 results in good levels of inter-laboratory agreement using both U–Pb decay schemes (Fig. 5). The final 2σ uncertainties of individual ²⁰⁶Pb $/$ ²³⁸U dates ranged from 0.05 % to 0.23 % (0.10 % to 0.47 % for ²⁰⁷Pb $/$ ²³⁵U) and were dominantly a function of the uncertainty assigned to α_Pb for the most precisely measured aliquots or α_Pb and uncertainties on measured Pb isotope ratios in others. At the stated precision levels, the reproducibility of 120 single PLES535 aliquot analyses in our experiment was very close to that expected from a homogeneous material for ²⁰⁶Pb $/$ ²³⁸U dates (MWSD = 1.5) and ²⁰⁷Pb $/$ ²³⁵U dates (MWSD = 1.2) but not for ²⁰⁷Pb $/$ ²⁰⁶Pb dates (MSWD = 2.2). Within-lab repeatability was also satisfactory, with nearly all datasets returning internal MWSD values consistent with analytical scatter around a single value for both U–Pb dates and the ²⁰⁷Pb $/$ ²⁰⁶Pb date (Table 2). However, a comparison of weighted means of dates from individual labs reveals systematic differences outside of the stated uncertainty. The level of agreement, given as 2 standard deviations of the population of lab weighted means, was 0.05 % for ²⁰⁶Pb $/$ ²³⁸U, 0.09 % for ²⁰⁷Pb $/$ ²³⁵U, and 0.62 % for ²⁰⁷Pb $/$ ²⁰⁶Pb (Fig. 5, Table 2). Interestingly, the deviations of sample/spike ratios in datasets 10, 11, 13, and 14 show strong correlations between Pb and U isotopes, resulting in consistent U–Pb dates despite scattering ratios. This effect mimics what would be expected if the relative proportions of spike and sample varied from aliquot to aliquot because the resulting ²⁰⁶Pb $/$ ²³⁸U dates vary less than the measured relative abundances of spike and sample. However, it is hard to understand how individual aliquots could have remained distinct through vigorous high temperature processing. Alternatively, some of this scatter could be due to small amounts of contamination with a Pb–U spike (with little sample) of similar composition, but this cannot explain analyses with higher measured ²³⁸U $/$ ²³³U. Regardless of the origin, this data pattern does not seem to strongly affect the overall results or the apparent dates, but when considered along with apparent problems equilibrating the “ET solutions” (Schaltegger et al., 2021), it suggests that this relates to an unresolved issue worth investigating in future work.

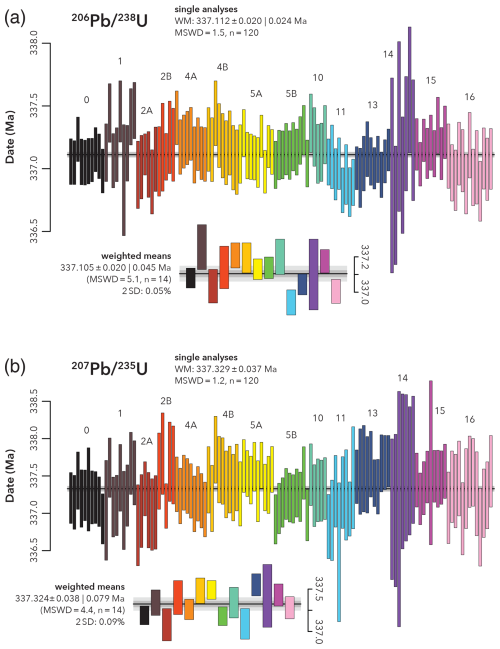
Figure 5 Reproducibility of individual ²⁰⁶Pb $/$ ²³⁸U (a) and ²⁰⁷Pb $/$ ²³⁵U (b) dates and the corresponding weighted means grouped by lab code. All data are reported with 2σ uncertainty represented as bar height. Uncertainty on weighted means is given in the form $\pm x|y$, where x represents the weighted mean uncertainty, and y additionally includes overdispersion in cases of excess scatter (e.g. Vermeesch, 2018).

4 Discussion

The design of our PLES535 experiment, where analyses were conducted on a homogeneous, pre-spiked solution rather than a population of naturally occurring zircon crystals, offers a unique opportunity to exclude geological bias from further consideration. As a result, we have obtained the first reliable community estimate of the reproducibility of ID-TIMS U–Pb geochronology methods as applied to natural zircon material that includes all post-dissolution laboratory preparation steps, mass spectrometry, and data reduction. The results show that following current methods and using variable hardware, all participating labs can produce weighted-mean ²⁰⁶Pb $/$ ²³⁸U ages of ²⁰⁵Pb-spiked, radiogenic samples that agree within 0.05 %. This level of agreement is better than the original EARTHTIME goal of 0.1 % interlaboratory reproducibility and serves to illustrate the progress made by the U–Pb community in the last 20 years. However, achieving levels of reproducibility commensurate with internal repeatability of each lab (as good as 0.02 % SD for ca. 10 analyses in this experiment) requires a more detailed look at the sources of random and systematic error in both mass spectrometry and subsequent corrections to isotope ratios. The design of the PLES535 study lends itself to both modelling these systematic errors and examining how they may explain the residual interlaboratory variance in reported isotopic ratios and their derived U–Pb dates.

We have modelled the perturbation of both Pb and U isotope ratio measurements resulting from systematic errors in mass-dependent fractionation, ion-counting detector dead time, Faraday detector response (arising from fluctuations in detector baseline, amplifier gain, or cup efficiency), isobaric interference on lead isotope masses, oxide correction of ¹⁸O-substituted ²³³UO₂ on ²³⁵UO₂, and uranium blank subtraction. In Fig. 6 we visualise these models in a bivariate format (²⁰⁶Pb $/$ ²⁰⁵Pb – ²⁰⁷Pb $/$ ²⁰⁶Pb and ²³³U $/$ ²³⁵U – ²³⁸U $/$ ²³⁵U) that reveals the vector of bias for each source of error, superposed with participating laboratory data. The Pb isotope ratios illustrated in Fig. 6a have been corrected for Pb blank contributions and the nominal mass fractionation factor (α_Pb) reported by each laboratory and as such illustrate residual bias in α_Pb in increments of ± %/amu. The effects of bias in the assumed dead time of the ion-counting system are illustrated in increments of ± fractions of a nanosecond, for three different major isotope (²⁰⁶Pb) count rates. Bias in Faraday detection (baseline, amplifier gain, and/or cup efficiency) is modelled generically in three models as perturbations of up to 200 ppm in each of the Faraday cups measuring ²⁰⁷Pb, ²⁰⁶Pb, and ²⁰⁵Pb in a static multicollection configuration. The effects of isobaric interferences on Pb isotopes are modelled as an excess on-peak count rate of up to 50 counts per second (cps) across all three masses (with 500 000 cps of ²⁰⁶Pb), in either equal proportions or a ratio of 2:1 odd over even masses.

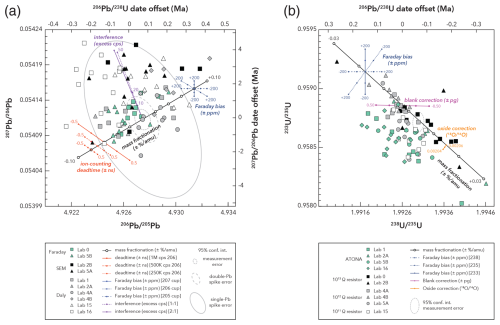
Figure 6 Reproducibility of key Pb (a) and U (b) isotope ratios analysed in PLES535. Measured ²⁰⁷Pb $/$ ²⁰⁶Pb and ²⁰⁶Pb $/$ ²⁰⁵Pb ratios were corrected for mass fractionation and lab blanks (Table 1). Measured ²³⁸U $/$ ²³⁵U and ²³³U $/$ ²³⁵U ratios were corrected only for oxide interferences (done by each lab individually). The quantified effects of various instrumental and data processing biases are illustrated as labelled vectors. Also illustrated are representative propagated 95 % confidence interval error ellipses for both measured U and Pb isotope ratios, as well as fractionation- and blank-corrected Pb isotope ratios.

The U isotope ratios in Fig. 6b are the reported (not mass fractionation corrected) measured isotope ratios from each laboratory, and as such their vector of variation is dominated by mass fractionation effects; however, other sources of systematic error can be visualised and quantified as scatter about this vector. For U isotope measurements, the effects of bias in assumed mass fractionation and Faraday detector performance follow the same parameterisations as for Pb isotopes. U oxide correction variability is modelled for a range in assumed ¹⁸O $/$ ¹⁶O from 0.00206 to 0.00204. The effects of an over-correction (+) or under-correction (−) in the amount of assumed U blank is modelled up to ±0.5 pg (with respect to a typical sample U content of 1.6 ng) with an assumed natural U isotopic composition (²³⁸U $/$ ²³⁵U = 137.818). Because of the enriched isotopic purity of the ETH-535 spike, models using blanks as mixtures of natural and spike isotopic compositions lie along identical trajectories and are not shown for clarity.

From our study, several key areas emerge as those with potential for improvement, with proposed solutions all in the general realm of mass spectrometry practice. Below we discuss each of them and provide suggestions about potential ways forward.

4.1 Reproducibility of Pb isotope ratios

About half of the datasets display excess scatter in fractionation- and blank-corrected Pb isotopic ratios (Fig. 4a). Other datasets are internally consistent but exhibit interlaboratory offsets (inset to Fig. 4a). This suggests a combination of (1) underestimated uncertainty on one or more of the components contributing to single-point uncertainty and (2) bias on some of the inputs required to calculate the Pb isotopic ratios. Since the sizes of the Pb loads were large by design (ca. 80 pg Pb^*), we can exclude the blank correction as a large potential source of error. This leaves three main areas that could be responsible: Pb fractionation correction, detector calibration/performance issues, and isobaric interferences on Pb isotope masses. Our modelled isotope ratios show that each of these sources of internal variability and systematic bias exhibits a characteristic vector and magnitude in isotope ratio space that can be compared to intra- and interlaboratory variance (Fig. 6a). We have further translated the resulting variability in isotope ratios into associated relative deviations in both ²⁰⁶Pb $/$ ²³⁸U and ²⁰⁷Pb $/$ ²⁰⁶Pb dates. To clarify this analysis, we have focused on a subset of 10 datasets that show the best repeatability; however, our conclusions almost certainly apply to the remaining laboratory data at larger magnitudes of variance and bias.

In Fig. 6a, the blank- and fractionation-corrected ²⁰⁶Pb $/$ ²⁰⁵Pb and ²⁰⁷Pb $/$ ²⁰⁶Pb scatter about a positively correlated array parallel to the vector of residual mass fractionation. This array is particularly apparent within the data acquired by Faraday cup detection (0, 5B) and a subset of four Daly ion-counting datasets (1, 2A, 4A, 4B). Pb isotope ratios measured on Faraday cups exhibit less variance, which is perhaps in part attributable to the lower magnitude of detector-related mass fractionation by Faraday detection in comparison to ion counters. If all of the observed variance was caused by residual mass fractionation offset, its magnitude within and between datasets would be ±0.06 %/amu, which corresponds to an apparent offset in ²⁰⁶Pb $/$ ²³⁸U date of ±0.25 Ma (0.075 %). This degree of variance is well described by the propagated errors of most laboratories (large error ellipse in Fig. 6a) but much larger than measurement uncertainties (small dashed error ellipse) or the degree of reproducibility achievable by double spike (²⁰²Pb $/$ ²⁰⁵Pb) fractionation correction (intermediate dashed error ellipse).

While residual bias in Pb fractionation is clearly a major source of variance, there is also scatter at a high angle from the fractionation vector. For Faraday cup detection, this degree of scatter can be explained by ±150 ppm variability in baseline, amplifier gain, or cup efficiency. Similarly for ion-counting detection, the fluctuations in ratios can be explained by variations of ±0.5 ns in the dead time of the ion-counting electronics for the four aforementioned Daly datasets. These detection-based fluctuations can contribute as much as ±0.05 Ma (0.015 %) of variability in the ²⁰⁶Pb $/$ ²³⁸U date. Interestingly, two other Daly datasets and two discrete-dynode secondary electron multiplier datasets exhibit excursions to significantly higher ²⁰⁷Pb $/$ ²⁰⁶Pb ratios, which could be a manifestation of greater degrees of detector nonlinearity (e.g. Richter et al., 2001). Alternatively, we note that these deviations, mainly in ²⁰⁷Pb $/$ ²⁰⁶Pb, are asymmetric to higher ratios. This is a modelled property of the effect of on-peak isobaric interferences on Pb isotopes, which creates a vector of variance nearly orthogonal to the fractionation trajectory. Such interferences are commonly seen at lower run temperatures using silica gel emitters and are thought to result from transient formation and transmission of heavy organic molecular ions. While such interferences are normally transient, as witnessed by a rise and plateau of ²⁰⁶Pb $/$ ²⁰⁴Pb (and ²⁰⁶Pb $/$ ²⁰⁷Pb) ratios during the early sequences of measurement, variability in the magnitude and persistence of interferences has been noted by several of the co-authors, and various source cleaning and heating protocols are used by laboratories to mitigate interferences. Interferences of a magnitude of up to 50 counts per second across the Pb isotope mass range could explain the excursions to highest ²⁰⁷Pb $/$ ²⁰⁶Pb in Fig. 6a. Fortunately, the steep trajectory of this interference vector produces a relatively minor younging of the ²⁰⁶Pb $/$ ²³⁸U date (≤ 0.05 Ma, or 0.015 % of 337 Ma) but does produce a much more substantial bias in ²⁰⁷Pb $/$ ²⁰⁶Pb (and ²⁰⁷Pb $/$ ²³⁵U) dates.

4.2 Recommendations for Pb isotope ratio mass spectrometry

It is apparent from Fig. 6a that for single Pb-spiked samples such as PLES535, corrections of mass fractionation in Pb analyses have overwhelming importance, and they may mask other effects affecting Pb isotopic results. The value and uncertainty of α_Pb are currently determined using a variety of protocols, some of which may be more appropriate to determine a correction for an unknown zircon than others. Most labs compile measurements of unspiked Pb isotopic standard reference materials (SRMs), such as NIST SRM 981 or 982, which are used to determine in-run mass fractionation from the deviation of one or more isotope ratios (typically ²⁰⁸Pb $/$ ²⁰⁶Pb, Table 1) from reference values. Others use zircon unknowns spiked with the EARTHTIME ²⁰²Pb–²⁰⁵Pb–²³³U–²³⁵U (ET2535) tracer and use the deviation of ²⁰²Pb $/$ ²⁰⁵Pb from reference to derive α_Pb. In principle, the mass fractionation correction should account for all mass-dependent isotope fractionation effects that occur within the mass spectrometer (and may include variations due to filament temperature, measurement duration, load on the filament, detector bias) and in sample preparation (dissolution, ion exchange chemistry; presumed to be unimportant). Consequently, close matching of the method to determine α_Pb with the methods used to prepare and analyse unknown zircons may be critical to estimate the accurate α_Pb and its uncertainty. The most conservative approach would be to use data collected during analyses of zircon samples processed through ion exchange chemistry, while the run temperature, load size, and consequent intensity would be closely matched between the α_Pb determination and the unknown run. An alternative approach using Pb SRM appropriate for labs without a double-Pb spike is likely suitable as well, since fractionation during analyses, rather than in ion exchange, appears to be the dominant effect; however, we are not aware of a detailed investigation of this issue in the literature. Regardless, greater care in determining α_Pb may go some way towards reducing the observed scatter.

Secondly, it is desirable when comparing fractionation-corrected data between many labs to ensure that they refer to the same standard values. While this is the case here for U isotopes (via the ²³³U–²³⁵U spike which is in common), the fractionation-corrected values of Pb isotope ratios of the ²⁰⁵Pb-spiked PLES535 ultimately depend on the composition of a Pb SRM used by each lab. This is the case because α_Pb is calibrated independently by each lab to a certain composition of either SRM 981/982 or the ET2535 spike, which itself is calibrated against SRM 981. Since the fractionation correction was applied on the instrument basis, differences in the used SRM values should lead to systematic shifts between datasets. Table 1 summarises the methods used to calibrate α_Pb and the reference ²⁰⁸Pb $/$ ²⁰⁶Pb value employed by each lab. The range of these values is 0.023 %; consequently, bringing all data to the same reference value will result in shifts not exceeding half of that value for ²⁰⁶Pb $/$ ²⁰⁵Pb or ²⁰⁷Pb $/$ ²⁰⁶Pb. While this is a significant offset from a single lab's perspective (e.g. if it used an extreme ²⁰⁸Pb $/$ ²⁰⁶Pb value), bringing the reference value in line does not bring about any improvement to interlaboratory reproducibility for the PLES535 dataset (i.e. it does not decrease the scatter of lab means). However, aligning the community to one reference value appears to be an easy step that should be taken immediately. Production of a new reference solution or an interlaboratory study of the composition of existing SRM may be good avenues for the future; until that time, we recommend that labs adopt the isotopic composition that was used to calibrate the respective isotopic tracer and report that value in publications. For ET(2)535 this is ²⁰⁸Pb $/$ ²⁰⁶Pb = 2.1681 for SRM 981, which is the value listed on the certificate of analysis. Both SRM 981 and 982 were calibrated directly against gravimetric Pb solutions, but it has been a long-standing practice of the Pb isotope community to use an isotopic composition of SRM 981 that is traceable to gravimetry via SRM 982 and a double-Pb spike. Doing so typically results in a ²⁰⁸Pb $/$ ²⁰⁶Pb of 2.1677 (e.g. Taylor et al., 2015), which is why some laboratories use this value or one close to it (Table 1). The divergence between different isotopic compositions apparently has not been identified before but is clearly a source of unnecessary interlaboratory bias.

The intermediate-sized (dashed) error ellipse in Fig. 6a illustrates the nominal uncertainty in Pb isotope ratios resulting from α_Pb correction and error propagation using the ET2535 double-Pb spike. It is apparent that the use of in-run double-spike quantification of α_Pb reduces the magnitude of fractionation correction such that other detection-related sources of random and systematic error become commensurate. To achieve intra- and interlaboratory reproducibility at the 0.01 % level will require even more careful attention to the dead time and linearity characteristics of ion-counting detectors targeting ±0.2 ns accuracy, and to the efficiency and baseline calibrations for Faraday cups and amplifiers, targeting better than ±50 ppm cup efficiency matching and baseline stability. Based on our limited dataset we suggest that Faraday detection of major Pb isotopes (as in datasets 0 and 5B) will be preferred over ion counters in the future as their achieved precision and reproducibility offer a clear advantage (Figs. 2, 6). We note that 8 out of 14 datasets in our experiment were produced on instruments that already have the capability to analyse ^205–208Pb in small (< 20 pg Pb^*) zircon samples in Faraday cups because they are equipped with low-noise amplifiers such as ATONA or the resistor-based 10¹³Ω amplifiers (von Quadt et al., 2016; Szymanowski and Schoene, 2020). If ionisation efficiency could be improved (Fig. 3), Faraday collection for a wider range of sample sizes would be within reach for most of the community.

4.3 Reproducibility of U isotope ratios

Oxide- and fractionation-corrected U isotopic ratios were reproduced similarly well to Pb within individual datasets but exhibit significant interlaboratory offsets (Fig. 4b). While this effect does not propagate into large differences in the final U–Pb dates of PLES535, it is likely to be significant for higher-precision (e.g. double-Pb-spiked) datasets. To explore the source of this overdispersion, we again turn to a bivariate U isotope space in which the datasets can be superimposed upon modelled vectors of mass fractionation, oxide interference, blank correction, and Faraday detector bias. In the case of U isotopes, we must revert to measured ²³⁸U $/$ ²³⁵U and ²³³U $/$ ²³⁵U (Fig. 6b). As in Fig. 6a, the same 10 datasets that show the best repeatability are illustrated here to assess the nature of both random and systematic error contributions. A representative 95 % confidence interval error ellipse for the measured isotope ratios is also illustrated. Datasets have been distinguished in this diagram by shading according to detector type, with resistor-based amplification systems illustrated in shades of white, grey, and black with increasing resistance, and ATONA amplifiers illustrated in colour.

In Fig. 6b, the uncorrected measured ²³⁸U $/$ ²³⁵U and ²³³U $/$ ²³⁵U scatter about an expected negatively correlated array parallel to the vector of mass fractionation. While the internal correction for mass fractionation using the double-U spike moves analyses parallel to this vector, it is straightforward to visualise the resulting collapsed near-horizontal band of analyses that exhibits the overdispersion noted above. In its expanded state, Fig. 6b illustrates and tests several hypotheses for the source of overdispersion. First, our modelling of the vector of dispersion associated with oxygen isotope variations from ¹⁸O $/$ ¹⁶O = 0.00204 to 0.00206 illustrates the very minor role (by design of the mixed ²³³U $/$ ²³⁵U tracer; Condon et al., 2015) of the oxide correction for precise and accurate U isotope measurements. Biases in ¹⁸O $/$ ¹⁶O are thus not responsible for the observed scatter. Isotope fractionation effects in ion exchange chemistry are also corrected for using the double spike; additionally, all aliquots in the experiment returned α_U comparable in value to the α_Pb determined for Faraday cup datasets, suggesting the bulk of mass fractionation occurred within the mass spectrometers. Excluding these effects, we suggest that the added scatter may instead be caused by non-systematic blank contributions or by detector biases exacerbated by static multicollection routines.

The ²³⁸U $/$ ²³⁵U ratios in Figs. 4b and 6b are not blank-corrected in an attempt to illustrate the effect of non-sample, non-tracer U present in the analysed material. The scatter in most individual datasets could apparently be explained by non-systematic blank contributions of up to ca. 0.5 pg U (compared to the sample U of 1.6 ng), with somewhat larger values necessary to explain datasets 10–14. Uranium blanks are not often systematically reported, resulting in a limited understanding of their magnitude and variability. Critically, if the scatter observed in Fig. 4b were purely due to blanks that are unaccounted for, it would imply that their mass is highly non-systematic. However, U blank values of up to 0.5 pg would exceed the mass of most measured Pb blanks and are a factor of 40 times greater than the U blanks reproducibly measured by Lab 4, which anchors the blank correction model in Fig. 6b. Consequently, we find it unlikely that either over- or under-correction for U blanks is of sufficient magnitude to explain the variance beyond fractionation for most lab datasets in Fig. 6b. We can further address one more source of uncertainty, namely that one potential source of U contamination in U–Pb labs is other samples analysed in these labs (such as carry-over of spiked aliquots remaining in labware), and thus it is conceivable that the U isotopic composition of this theoretical contaminant is highly variable and distinct from the silicate Earth ²³⁸U $/$ ²³⁵U values. However, our modelling demonstrates that the trajectory of blank effects on isotope ratios is completely insensitive to mixing between spike and natural U isotopic compositions (Table S1).

An alternative and more likely explanation of the scatter in U isotopic analyses involves biases inherent to the TIMS analytical setups. All of the datasets illustrated in Fig. 6b were acquired in a static multicollection routine on 3–4 Faraday cups, such that short-term variations in Faraday baseline, amplifier gain, or cup efficiency are a potential source of added scatter in the results. Cup efficiencies may also play a role in more systematic inter-laboratory variations. It is apparent that the dispersion along the fractionation array defined by the resistor-based Faraday amplifier U isotope data can be explained by ±100 ppm of detector variability and bias. Given the ppm-level stability of most amplifier gain calibrations (e.g. Szymanowski and Schoene, 2020), this is a less likely source of dispersion. Similarly, Faraday cup efficiencies are likely stable at ± 10 ppm levels for a given static detector geometry over the short measurement times in which the PLES535 data were typically acquired within each lab (Di et al., 2021). As a result, we suggest that intra-laboratory dispersion for a given fixed static Faraday collector geometry is more likely related to subtle baseline variability. This degree of ratio dispersion translates into as much as ± 0.075 Ma (0.023 %) of variability in the ²⁰⁶Pb $/$ ²³⁸U date.

Interestingly, it is also apparent that the resistor-based amplification systems and ATONA capacitive transimpedance amplifier systems generally define two different correlated fractionation arrays separated by a ∼ 200 ppm offset. However, in detail there is mutual overlap between some of these detection systems on a laboratory basis. Of significant note are two ATONA datasets (Lab 1 and Lab 2A) that illustrate remarkable internal collinearity but are offset from each other by 200 to 250 ppm depending upon the collector to which the efficiency bias is attributed. As a result, we do not suggest that the two amplification systems have fundamentally different characteristics but rather that the Faraday cup efficiencies of different manufacture and generations of instruments have some systematic variability. Taken together, all these data suggest that Faraday cup efficiency differences as great as 200 ppm, and Faraday cup baseline fluctuations at the ± 100 ppm level, are the predominant sources of systematic bias and random dispersion in U isotope ratio measurements between and within datasets.

4.4 Recommendations for U isotope ratio mass spectrometry

Although we find little clear evidence of profound effects related to U blank subtraction in the PLES535 experiment, continued systematic survey of U blank amounts in each laboratory remains strongly advised, as this can be significant for small samples, particularly those that have a high ratio of radiogenic Pb to U. Regarding intra-laboratory repeatability, the most impactful mass spectrometric investigations likely centre around improved detector baseline characterisation during analysis, including optimisation of integration times and baseline versus on-peak duty cycle, and the development or adoption of methods of cancelling biases between Faraday detectors such as relative cup efficiency characterisation (Makishima and Nakamura, 1991; Miyazaki et al., 2016; Davis, 2020; Di et al., 2021), amplifier rotation, or multi-dynamic acquisition of U. Reference material IRMM-199 has a ²³³U $/$ ²³⁵U $/$ ²³⁸U similar to that of ²³³U–²³⁵U-spiked zircon and would be well suited to test such protocols.

5 Next steps

The results of our interlaboratory experiment demonstrate that 14 variably equipped instruments at 11 participating ID-TIMS labs can reproduce ²⁰⁶Pb $/$ ²³⁸U and ²⁰⁷Pb $/$ ²³⁵U ages for a homogeneous starting material to within 0.05 % and 0.09 %, respectively, underscoring the reliability of ID-TIMS U–Pb geochronology as a tool to constrain time in Earth and planetary sciences, as well as to calibrate lower-precision U–Pb analytical methods.

While the level of agreement found here is a testament to the analytical rigour and cooperation that have characterised the ID-TIMS U–Pb community in the last 20 years, we have also identified areas for further methodological refinement. Due to the limited availability of ²⁰²Pb, in this experiment we used a single ²⁰⁵Pb spike, which meant that the largest source of uncertainty in all the analyses was the mass fractionation of Pb during mass spectrometry. When this uncertainty is minimised by ²⁰²Pb–²⁰⁵Pb double-spike measurements, then other sources of uncertainty need to be targeted to achieve interlaboratory reproducibility at the 0.01 % level in future work. In the quest of achieving reproducibility commensurate with internal repeatability of single labs, we propose the following action points for the community regarding further method development:

1. If using isotopic reference materials to estimate mass fractionation during Pb analyses, we recommend using the values employed to calibrate the tracer. For EARTHTIME spikes, this should be ²⁰⁸Pb $/$ ²⁰⁶Pb = 2.1681 of SRM 981.

2. In calibrating α_Pb, closely match the measurement conditions of the reference material and unknown, preferably using compiled double-spiked zircon analyses to determine α_Pb.

3. Both ²⁰²Pb and ²⁰⁵Pb have not been produced for decades, and there is no current plan to replenish their stocks. This study highlights how critical using both isotopes simultaneously is for the best possible measurements. It is critical that new stocks be produced in the coming decade so that a new double-Pb, double-U community tracer can be prepared.

4. Develop common protocols for the characterisation and reporting of ion detector performance. This includes the measurement of the dead time (with a target of ±0.2 ns) and linearity of ion counters, electronic baselines and true backgrounds of Faraday cup arrays, and Faraday cup efficiencies (with a target of ±50 ppm).

5. High-quality measurements depend on high ionisation efficiency, but the best ion emitters may be difficult to obtain. The best ionisation efficiency for UO₂ is obtained using Merck article 12475 (Gerstenberger and Haase, 1997); however this reagent has been long off the market. Other activators may work well for Pb but may have worse blank levels (e.g. Huyskens et al., 2012). Developing easily accessible, common activators that work well will help every lab produce the highest-quality data, e.g. by enabling Faraday detection of smaller samples of Pb.

6. Characterise the mass of U blanks and their variability with the same care that Pb blanks are monitored.

Further progress in method improvement in these areas should make it possible to achieve a new goal of 0.01 % interlaboratory reproducibility, which will be close to the currently best achievable analytical precision.

6 Implications for geologic studies

To conclude, we highlight implications of our interlaboratory comparison for the practical application of ID-TIMS U–Pb geochronological data to geological problems by a non-specialist user. This is intended as a short set of guidelines aiding the planning of future studies as well as the interpretation of existing age data considering the current limits on repeatability and reproducibility:

• Internally, ID-TIMS labs in our experiment can obtain indistinguishable U–Pb dates for multiple aliquots of a homogeneous zircon solution (n = 5 to 10). This indicates that uncertainties are generally not underestimated. Consequently, obtaining non-overlapping ID-TIMS U–Pb dates on zircon unknowns from the same lab, one can have certainty (to the quoted level of confidence) that these dates are different. This statement is valid for analytical methods, but geological reasons for apparent age discrepancies, such as Pb loss, should always be kept in mind.

• The current level of interlaboratory reproducibility is 0.05 % for the ²⁰⁶Pb $/$ ²³⁸U method commonly applied throughout the Phanerozoic, as tested here for near-optimal, highly radiogenic samples. However, precision, repeatability, and inter-lab reproducibility of dates for samples that have less radiogenic Pb than PLES535 (because they are small or young) may be worse than presented here because they are critically limited by the accuracy and precision of Pb blank corrections. While the community strives to characterise blanks accurately, Pb contamination remains a source of added uncertainty for non-radiogenic samples. Likewise, old-rock applications relying on the use of ²⁰⁷Pb $/$ ²⁰⁶Pb dates present their own set of challenges centred around the accuracy of Pb isotope analyses, and the reproducibility of such analyses may differ from the result obtained here for ²⁰⁶Pb $/$ ²³⁸U.

• If the necessary (or expected) dating resolution for a project is > 0.05 % and ultimate analytical precision is not required (e.g. in young rocks), mixing dates from multiple labs that use the same tracer is not a problem. But to resolve age differences beyond this level, we recommend conducting analyses at only one lab to minimise systematic biases, and for the lab to keep lab practices consistent for the duration of such a project. Alternatively, if using more than one lab, at least one sample should be dated by all the labs to indicate the level of comparability. The decision to involve more than one lab should be based on the expected timescale of the studied process and the expected and necessary time resolution.

• For the ultimate accuracy of dates such as that required for the definition of stage boundaries of the Geologic Time Scale, it would be advisable to propagate the uncertainty stemming from interlaboratory reproducibility onto final boundary ages. This will have a small effect on the overall uncertainty given that systematic uncertainties are often considered (due to a mix of multiple radioisotopic systems used), but it will lead to a more realistic comparison of the U–Pb age constraints themselves.

• ID-TIMS U–Pb from a single lab remains a valid choice for the characterisation of zircon reference materials for microanalytical U–Pb geochronology as the precision and accuracy required for these methods is more than an order of magnitude worse than the level of interlaboratory reproducibility documented here.