Unifying the U–Pb and Th–Pb methods: joint isochron regression and common Pb correction

The actinide elements U and Th undergo radioactive decay to three isotopes of Pb, forming the basis of three coupled geochronometers. The ²⁰⁶Pb ∕²³⁸U and ²⁰⁷Pb ∕²³⁵U decay systems are routinely combined to improve accuracy. Joint consideration with the ²⁰⁸Pb ∕²³²Th decay system is less common. This paper aims to change this. Co-measured ²⁰⁸Pb ∕²³²Th is particularly useful for discordant samples containing variable amounts of non-radiogenic (“common”) Pb.

The paper presents a maximum likelihood algorithm for joint isochron regression of the ²⁰⁶Pb ∕²³⁸Pb, ²⁰⁷Pb ∕²³⁵Pb and ²⁰⁸Pb ∕²³²Th chronometers. Given a set of cogenetic samples, this $\mathrm{total}-\mathrm{Pb}/\mathrm{U}-\mathrm{Th}$ algorithm estimates the common Pb composition and concordia intercept age. U–Th–Pb data can be visualised on a conventional Wetherill or Tera–Wasserburg concordia diagram, or on a ²⁰⁸Pb ∕²³²Th vs. ²⁰⁶Pb ∕²³⁸U plot. Alternatively, the results of the new discordia regression algorithm can also be visualised as a ²⁰⁸Pb_c ∕²⁰⁶Pb vs. ²³⁸U ∕²⁰⁶Pb or ²⁰⁸Pb_c ∕²⁰⁷Pb vs. ²³⁵U ∕²⁰⁶Pb isochron, where ²⁰⁸Pb_c represents the common ²⁰⁸Pb component. In its most general form, the $\mathrm{total}-\mathrm{Pb}/\mathrm{U}-\mathrm{Th}$ algorithm accounts for the uncertainties of all isotopic ratios involved, including the ²³²Th ∕²³⁸U ratio, as well as the systematic uncertainties associated with the decay constants and the ²³⁸U ∕²³⁵U ratio. However, numerical stability is greatly improved when the dependency on the ²³²Th ∕²³⁸U-ratio uncertainty is dropped.

For detrital minerals, it is generally not safe to assume a shared common Pb composition and concordia intercept age. In this case, the $\mathrm{total}-\mathrm{Pb}/\mathrm{U}-\mathrm{Th}$ regression method must be modified by tying it to a terrestrial Pb evolution model. Thus, also detrital common Pb correction can be formulated in a maximum likelihood sense.

The new method was applied to three published datasets, including low Th∕U carbonates, high Th∕U allanites and overdispersed monazites. The carbonate example illustrates how the $\mathrm{total}-\mathrm{Pb}/\mathrm{U}-\mathrm{Th}$ method achieves a more precise common Pb correction than a conventional ²⁰⁷Pb-based approach does. The allanite sample shows the significant gain in both precision and accuracy that is made when the Th–Pb decay system is jointly considered with the U–Pb system. Finally, the monazite example is used to illustrate how the $\mathrm{total}-\mathrm{Pb}/\mathrm{U}-\mathrm{Th}$ regression algorithm can be modified to include an overdispersion parameter.

All the parameters in the discordia regression method (including the age and the overdispersion parameter) are strictly positive quantities that exhibit skewed error distributions near zero. This skewness can be accounted for using the profile log-likelihood method or by recasting the regression algorithm in terms of logarithmic quantities. Both approaches yield realistic asymmetric confidence intervals for the model parameters. The new algorithm is flexible enough that it can accommodate disequilibrium corrections and intersample error correlations when these are provided by the user. All the methods presented in this paper have been added to the IsoplotR software package. This will hopefully encourage geochronologists to take full advantage of the entire U–Th–Pb decay system.

1 Introduction

The Pb content of U-bearing minerals comprises two components:

1. Non-radiogenic (a.k.a. initial or “common”) Pb is inherited from the environment during crystallisation. It contains all of lead's four stable isotopes (²⁰⁴Pb, ²⁰⁶Pb, ²⁰⁷Pb and ²⁰⁸Pb) in fixed proportions for a given sample.

2. Radiogenic Pb is added to the common Pb after crystallisation due to the decay of U and Th. It contains only three isotopes (²⁰⁶Pb, ²⁰⁷Pb and ²⁰⁸Pb), which occur in variable proportions as a function of the Th∕U ratio and age.

Denoting the measured and non-radiogenic components with subscripts “m” and “c”, respectively, and assuming initial secular equilibrium, we can write

$$\begin{array}{}\text{(1)}& {\displaystyle }& {\displaystyle }{}^{\mathrm{204}}{\mathrm{Pb}}_{\mathrm{m}}={}^{\mathrm{204}}{\mathrm{Pb}}_{\mathrm{c}}\text{(2)}& {\displaystyle }& {\displaystyle }{}^{\mathrm{206}}{\mathrm{Pb}}_{\mathrm{m}}={}^{\mathrm{206}}{\mathrm{Pb}}_{\mathrm{c}}+{}^{\mathrm{238}}{\mathrm{U}}_{\mathrm{m}}\left(e^{{\mathit{\lambda }}_{\mathrm{38}}t}-\mathrm{1}\right)\text{(3)}& {\displaystyle }& {\displaystyle }{}^{\mathrm{207}}{\mathrm{Pb}}_{\mathrm{m}}={}^{\mathrm{207}}{\mathrm{Pb}}_{\mathrm{c}}+{}^{\mathrm{235}}{\mathrm{U}}_{\mathrm{m}}\left(e^{{\mathit{\lambda }}_{\mathrm{35}}t}-\mathrm{1}\right)\text{(4)}& {\displaystyle }& {\displaystyle }{}^{\mathrm{208}}{\mathrm{Pb}}_{\mathrm{m}}={}^{\mathrm{208}}{\mathrm{Pb}}_{\mathrm{c}}+{}^{\mathrm{232}}{\mathrm{Th}}_{\mathrm{m}}\left(e^{{\mathit{\lambda }}_{\mathrm{32}}t}-\mathrm{1}\right),\end{array}$$

where λ₃₈, λ₃₅ and λ₃₂ are the decay constants of ²³⁸U, ²³⁵U and ²³²Th, respectively, and t is the time elapsed since isotopic closure. In order to accurately estimate t, the common Pb composition is needed. One way to account for common Pb is to normalise all the measurements to ²⁰⁴Pb. For example, using the ²³⁸U–²⁰⁶Pb decay scheme:

$$\begin{array}{}\text{(5)}& {\left[{\displaystyle \frac{{}^{\mathrm{206}}\mathrm{Pb}}{{}^{\mathrm{204}}\mathrm{Pb}}}\right]}_{\text{m}}={\left[{\displaystyle \frac{{}^{\mathrm{206}}\mathrm{Pb}}{{}^{\mathrm{204}}\mathrm{Pb}}}\right]}_{\text{c}}+{\left[{\displaystyle \frac{{}^{\mathrm{238}}\mathrm{U}}{{}^{\mathrm{204}}\mathrm{Pb}}}\right]}_{\text{m}}\left(e^{{\mathit{\lambda }}_{\mathrm{38}}t}-\mathrm{1}\right).\end{array}$$

Applying Eq. (5) to multiple cogenetic aliquots of the same sample defines an isochron with slope $\left(e^{{\mathit{\lambda }}_{\mathrm{38}}t}-\mathrm{1}\right)$ and intercept ${\left[{}^{\mathrm{206}}\mathrm{Pb}/{}^{\mathrm{204}}\mathrm{Pb}\right]}_c$. Alternatively, and equivalently, an “inverse” isochron line can be defined as

$$\begin{array}{}\text{(6)}& {\left[{\displaystyle \frac{{}^{\mathrm{204}}\mathrm{Pb}}{{}^{\mathrm{206}}\mathrm{Pb}}}\right]}_{\text{m}}={\left[{\displaystyle \frac{{}^{\mathrm{204}}\mathrm{Pb}}{{}^{\mathrm{206}}\mathrm{Pb}}}\right]}_{\text{c}}\left\{\mathrm{1}-{\left[{\displaystyle \frac{{}^{\mathrm{238}}\mathrm{U}}{{}^{\mathrm{206}}\mathrm{Pb}}}\right]}_{\text{m}}\left(e^{{\mathit{\lambda }}_{\mathrm{38}}t}-\mathrm{1}\right)\right\}.\end{array}$$

In this case, the isochron is a line whose y intercept defines the common ²⁰⁴Pb ∕²⁰⁶Pb ratio, and the x intercept determines the radiogenic ²³⁸U ∕²⁰⁶Pb ratio.

The isochron concept can easily be applied to the ²³⁵U–²⁰⁷Pb system, by replacing ²⁰⁶Pb with ²⁰⁷Pb, ²³⁸Pb with ²³⁵Pb and λ₃₈ with λ₃₅ in Eqs. (5) and (6). The accuracy and precision of the calculation can be further improved by solving the ²⁰⁶Pb ∕²³⁸U and ²⁰⁷Pb ∕²³⁵U isochron equations simultaneously and requiring t to be the same in both systems. The resulting three-dimensional constrained isochron is known as a total-Pb∕U isochron (Ludwig, 1998).

In igneous samples, the conventional total-Pb∕U isochron requires isotopic data for two or more cogenetic aliquots. In the simplest case, a two-point isochron can be formed by analysing the U–Pb composition of the U-bearing phase of interest along with a cogenetic mineral devoid of U (e.g., feldspar). In detrital samples, the common Pb intercept of the isochron can be anchored to some nominal value or to a terrestrial Pb evolution model (e.g., Stacey and Kramers, 1975). Thus, the ²⁰⁴Pb-based total-Pb∕U isochron method is beneficial to nearly all applications of the U–Pb method.

Unfortunately, ²⁰⁴Pb-based common Pb correction is not always practical. First, not all mass spectrometers are able to measure ²⁰⁴Pb with sufficient precision and accuracy. In some inductively coupled plasma mass spectrometry (ICP-MS) instruments, the presence of an isobaric interference with ²⁰⁴Hg precludes accurate ²⁰⁴Pb measurements. And second, because ²⁰⁴Pb is by far the least abundant of lead's four naturally occurring isotopes, it requires the longest dwell times. For single collector instruments, this reduces the precision of the other isotopes.

To overcome these problems, alternative common Pb correction schemes have been proposed that use ²⁰⁷Pb or ²⁰⁸Pb instead of ²⁰⁴Pb. The semitotal-Pb∕U isochron method is based on linear regression of ²⁰⁶Pb–²⁰⁷Pb–²³⁸U data in Tera–Wasserburg space (Ludwig, 1998; Williams, 1998; Chew et al., 2011). It assumes that all the samples are cogenetic and form a simple two-component mixture between common Pb and radiogenic Pb. The common Pb then marks the intercept with the ²⁰⁷Pb ∕²⁰⁶Pb axis, and the radiogenic Pb can be obtained from the intersection of the isochron with the concordia line. The ²⁰⁷Pb-based common Pb correction only works if the assumption of initial concordance is valid, if ²⁰⁷Pb can be measured with sufficient precision, and if there is enough spread in the initial Pb∕U ratios to produce a statistically robust isochron.

Andersen (2002) introduced a ²⁰⁸Pb-based common Pb correction scheme that does not require initial concordance. His method assumes that U–Th–Pb discordance can be accounted for by a combination of Pb loss at a defined time and the presence of common Pb of known composition. However, in most cases, neither the timing of Pb loss nor the composition of the common Pb are known. Furthermore, the assumptions that underlie the Andersen (2002) method were tailored to the mineral zircon but do not apply so much to other minerals such as carbonates, which crystallise at low temperatures and do not experience diffusive Pb loss.

This paper introduces a $\mathrm{total}-\mathrm{Pb}/\mathrm{U}-\mathrm{Th}$ isochron algorithm that uses the ²³²Th–²⁰⁸Pb decay scheme to determine the common Pb component. Unlike the Andersen (2002) method, it does not require the common Pb composition to be pre-specified but assumes that no Pb loss has occurred. The new algorithm is based on Ludwig (1998)'s total-Pb∕U isochron method but uses ²⁰⁸Pb_c instead of ²⁰⁴Pb in Eq. (5):

$$\begin{array}{}\text{(7)}& {\displaystyle \frac{{}^{\mathrm{206}}{\mathrm{Pb}}_{\mathrm{m}}}{{}^{\mathrm{208}}{\mathrm{Pb}}_{\mathrm{c}}}}={\left[{\displaystyle \frac{{}^{\mathrm{206}}\mathrm{Pb}}{{}^{\mathrm{208}}\mathrm{Pb}}}\right]}_c+{\displaystyle \frac{{}^{\mathrm{238}}{\mathrm{U}}_{\mathrm{m}}}{{}^{\mathrm{208}}{\mathrm{Pb}}_{\mathrm{c}}}}\left(e^{{\mathit{\lambda }}_{\mathrm{38}}t}-\mathrm{1}\right),\end{array}$$

and similarly for Eq. (6) and the ²³⁵U–²⁰⁷Pb equivalents of Eqs. (5) and (6).

The algorithms introduced in this paper will be illustrated using three published U–Th–Pb datasets, which showcase how the combined U–Th–Pb approach improves both the precision and accuracy of U–Pb geochronology (Sect. 4). The cases studies include a carbonate dataset of Parrish et al. (2018), an allanite dataset of Janots and Rubatto (2014) and an overdispersed monazite dataset of Gibson et al. (2016). The carbonate dataset is an example of a low Th∕U setting in which the ²⁰⁸Pb-based common Pb correction is more precise than a conventional ²⁰⁷Pb ∕²⁰⁶Pb-based common Pb correction. The allanite dataset is an example of a high Th∕U setting in which the ²⁰⁸Pb ∕²³²Th method offers greater precision than the U–Pb method. The Janots and Rubatto (2014) study used the Secondary Ion Mass Spectrometer (SIMS) and therefore also offers an opportunity to compare the new ²⁰⁸Pb method with a conventional ²⁰⁴Pb-based common Pb correction.

Section 5 shows how the isochron regression algorithm can be modified to accommodate strongly skewed uncertainty distributions, using a simple logarithmic change of variables. The $\mathrm{total}-\mathrm{Pb}/\mathrm{U}-\mathrm{Th}$ isochron algorithm assumes that all aliquots are cogenetic. However, Sect. 6 shows how the algorithm can be adapted to detrital samples, by tying it to the two-stage Pb evolution model of Stacey and Kramers (1975). This procedure is similar in spirit to the iterative algorithm of Chew et al. (2011) but uses a maximum likelihood approach that weights the uncertainties of all isotopes in the coupled U–Th–Pb decay system. Finally, Sect. 7 introduces an implementation of the algorithms described herein using the IsoplotR software package.

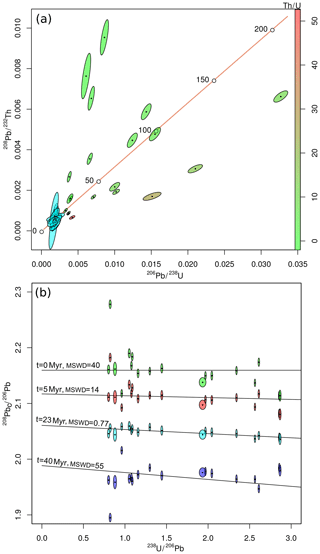
Figure 1 U–Th–Pb data for allanite sample MF482 of Janots and Rubatto (2014) shown on (a) a U–Th–Pb concordia diagram and (b) a ²⁰⁸Pb_c ∕²⁰⁶Pb–²³⁸U ∕²⁰⁶Pb isochron plot. The raw data are shown in shades of green to red on the concordia diagram, in proportion to the Th∕U ratio. The same raw data are shown as green ellipses on the isochron diagram. Red, light and dark blue ellipses show the measurements with 5, 23 and 40 Myr worth of radiogenic ²⁰⁸Pb removed, respectively. The misfit of the radiogenic ²⁰⁸Pb-corrected data around the best fit line are expressed as the mean square of the weighted deviates (MSWD; McIntyre et al., 1966) values. Error ellipses are shown at 1σ.

2 U–Th–Pb concordia and the $\mathrm{total}-\mathrm{Pb}/\mathrm{U}-\mathrm{Th}$ isochron

In conventional U–Pb geochronology, the set of concordant ²⁰⁶Pb ∕²³⁸U and ²⁰⁷Pb ∕²³⁵U ratios defines a Wetherill concordia line. Similarly, U–Th–Pb data can be visualised in ²⁰⁸Pb ∕²³²Th- vs. ²⁰⁶Pb ∕²³⁸U-ratio space. In the absence of common Pb, samples whose ²⁰⁸Pb ∕²³²Th ages equal their ²⁰⁶Pb ∕²³⁸U ages plot on a U–Th–Pb concordia line. The addition of common Pb pulls samples away from this line. Binary mixing between common Pb and radiogenic Pb forms linear trends in conventional concordia space but not in U–Th–Pb concordia space. For example the Janots and Rubatto (2014) data plot above or below the concordia line depending on the Th∕U ratio (Fig. 1a).

An alternative visualisation is to plot ²⁰⁸Pb ∕²⁰⁶Pb against ²³⁸U ∕²⁰⁶Pb (Fig. 1b). The radiogenic ²⁰⁸Pb component can be removed by rearranging Eq. (4) for ²⁰⁸Pb_c ∕²³²Th_m and subtracting it from [²⁰⁸Pb ∕²³²Th]_m. Doing this for different values of t moves the various aliquots vertically on the diagram. Each value of t also corresponds to a radiogenic ²³⁸U ∕²⁰⁶Pb ratio, thus marking a point on the horizontal axis of the diagram. We can fit a line through this point and minimise the residual scatter of the data around it, using a least squares criterion such as the mean square of the weighted deviates (MSWD; McIntyre et al., 1966). For the Janots and Rubatto (2014) data, the residual scatter is minimised when t≈23 Myr (Fig. 1b). At this value, the aliquots plot along a simple binary mixture between common Pb and radiogenic Pb. This marks the best estimate for the concordia age. The corresponding common-Pb-corrected ²⁰⁸Pb ∕²³²Th–²⁰⁶Pb ∕²³⁸U composition is shown as a tight cluster of blue error ellipses on Fig. 1a.

In order to formalise this procedure in a mathematical sense, let us first define a number of variables. In analogy to the variable names used by Ludwig (1998), we will refer to the blank corrected isotopic ratios as X, Y, Z, W and U:

$$\begin{array}{}\text{(8)}& \begin{array}{rl}& \mathit{X}={\left[{\displaystyle \frac{{}^{\mathrm{207}}\mathrm{Pb}}{{}^{\mathrm{235}}\mathrm{U}}}\right]}_{\text{m}},\mathit{Y}={\left[{\displaystyle \frac{{}^{\mathrm{206}}\mathrm{Pb}}{{}^{\mathrm{238}}\mathrm{U}}}\right]}_{\text{m}},\mathit{Z}={\left[{\displaystyle \frac{{}^{\mathrm{208}}\mathrm{Pb}}{{}^{\mathrm{232}}\mathrm{Th}}}\right]}_{\text{m}},\\ & \mathbf{W}={\left[{\displaystyle \frac{{}^{\mathrm{232}}\mathrm{Th}}{{}^{\mathrm{238}}\mathrm{U}}}\right]}_{\text{m}},U=\left[{\displaystyle \frac{{}^{\mathrm{238}}\mathrm{U}}{{}^{\mathrm{235}}\mathrm{U}}}\right],\end{array}\end{array}$$

where X, Y and Z are vectors, W is a diagonal matrix, and U is a scalar; we will use Greek characters for the unknown common Pb ratios:

$$\begin{array}{}\text{(9)}& \mathit{\alpha }={\left[{\displaystyle \frac{{}^{\mathrm{206}}\mathrm{Pb}}{{}^{\mathrm{208}}\mathrm{Pb}}}\right]}_c,\mathit{\beta }={\left[{\displaystyle \frac{{}^{\mathrm{207}}\mathrm{Pb}}{{}^{\mathrm{208}}\mathrm{Pb}}}\right]}_c,\mathit{\gamma }={\displaystyle \frac{{}^{\mathrm{208}}{\mathrm{Pb}}_{\mathrm{c}}}{{}^{\mathrm{232}}{\mathrm{Th}}_{\mathrm{m}}}},\end{array}$$

where α and β are scalars and γ is a vector; and finally, we will use t as the concordia age so as to satisfy Eqs. (1)–(4).

$$\begin{array}{}\text{(10)}& \begin{array}{rl}& {\left[{\displaystyle \frac{{}^{\mathrm{208}}\mathrm{Pb}}{{}^{\mathrm{232}}\mathrm{Th}}}\right]}_{\ast }=e^{{\mathit{\lambda }}_{\mathrm{32}}t}-\mathrm{1},{\left[{\displaystyle \frac{{}^{\mathrm{207}}\mathrm{Pb}}{{}^{\mathrm{235}}\mathrm{U}}}\right]}_{\ast }=e^{{\mathit{\lambda }}_{\mathrm{35}}t}-\mathrm{1},\\ & {\left[{\displaystyle \frac{{}^{\mathrm{206}}\mathrm{Pb}}{{}^{\mathrm{238}}\mathrm{U}}}\right]}_{\ast }=e^{{\mathit{\lambda }}_{\mathrm{38}}t}-\mathrm{1}\end{array}\end{array}$$

Next, we define three misfit vectors (K, L and M) containing the difference between the measured and the predicted (i.e., common plus radiogenic) isotope ratios:

$$\begin{array}{}\text{(11)}& {\displaystyle }& {\displaystyle }\mathit{K}=\mathit{X}-U\mathit{\beta }\mathbf{W}\mathit{\gamma }-e^{{\mathit{\lambda }}_{\mathrm{35}}t}+\mathrm{1}\text{(12)}& {\displaystyle }& {\displaystyle }\mathit{L}=\mathit{Y}-\mathit{\alpha }\mathbf{W}\mathit{\gamma }-e^{{\mathit{\lambda }}_{\mathrm{38}}t}+\mathrm{1}\text{(13)}& {\displaystyle }& {\displaystyle }\mathit{M}=\mathit{Z}-\mathit{\gamma }-e^{{\mathit{\lambda }}_{\mathrm{32}}t}+\mathrm{1}.\end{array}$$

This formulation is a straightforward adaptation of Ludwig (1998)'s ²⁰⁴Pb-based total-Pb∕U isochron equations. And like Ludwig (1998), we can then estimate t, α and β by minimising the sum of squares:

$$\begin{array}{}\text{(14)}& S=\mathbf{\Delta }{\mathbf{\Sigma }}_{\mathrm{\Delta }}^{-\mathrm{1}}{\mathbf{\Delta }}^{\text{T}},\end{array}$$

where Δ is the amalgamated misfit vector and Δ^T is its transpose (i.e., Δ^T=[K^TL^TM^T]). Σ_Δ is the covariance matrix of Δ, which can be estimated by error propagation:

$$\begin{array}{}\text{(15)}& {\mathbf{\Sigma }}_{\mathrm{\Delta }}=\left[\begin{array}{cc}{\mathbf{J}}_x& {\mathbf{J}}_{\mathit{\lambda }}\end{array}\right]\left[\begin{array}{cc}{\mathbf{\Sigma }}_x& {\mathrm{0}}_{\mathrm{4}n\times \mathrm{4}}\\ {\mathrm{0}}_{\mathrm{4}\times \mathrm{4}n}& {\mathbf{\Sigma }}_{\mathit{\lambda }}\end{array}\right]\left[\begin{array}{c}{\mathbf{J}}_x^{\text{T}}\\ {\mathbf{J}}_{\mathit{\lambda }}^{\text{T}},\end{array}\right]\end{array}$$

in which 0_a×b is an a×b matrix of zeros, Σ_x is the 4n×4n covariance matrix of the collated data measurements X, Y, Z and W; Σ_λ is the 4×4 covariance matrix of the decay constants and U, and J_x and J_λ are Jacobian matrices with partial derivatives of Δ with respect to the isotopic ratio measurements and the decay constants (plus U), respectively. Further details for Σ_x, Σ_λ, J_x and J_λ are provided in Appendix A.

Equation (14) can be solved for t, α and β by iterative methods, but the numerical stability of these methods is not guaranteed. Numerical stability and speed of convergence are greatly improved by removing the uncertainties of W from the data covariance matrix Σ_x. If the sum of squares S does not depend on the uncertainty of W, then the partial derivatives of S with respect to α, β, γ and t can be calculated manually, which greatly simplifies the optimisation. Further details about this simplified algorithm are provided in Appendix B.

3 Error propagation and overdispersion

The log likelihood of the isochron fit is given by

$$\begin{array}{}\text{(16)}& \mathcal{L}=-{\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}\left[\mathrm{3}n\ln \left(\mathrm{2}\mathit{\pi }\right)+\ln \left|{\mathbf{\Sigma }}_{\mathrm{\Delta }}\right|+S\right],\end{array}$$

where $\left|{\mathbf{\Sigma }}_{\mathrm{\Delta }}\right|$ marks the determinant of Σ_Δ. The covariance matrix of the fit parameters is then obtained by inverting the matrix of second derivates of the negative log likelihood with respect to the vector γ and the scalars t, α, β. This is also known as the Fisher information matrix:

$$\begin{array}{}\text{(17)}& \begin{array}{rl}& \left[\begin{array}{cccc}{\mathbf{\Sigma }}_{\mathit{\gamma }}& s[\mathit{\gamma },t]& s[\mathit{\gamma },\mathit{\alpha }]& s[\mathit{\gamma },\mathit{\beta }]\\ s[t,\mathit{\gamma }]& s[t{]}^{\mathrm{2}}& s[t,\mathit{\alpha }]& s[t,\mathit{\beta }]\\ s[\mathit{\alpha },\mathit{\gamma }]& s[\mathit{\alpha },t]& s[\mathit{\alpha }{]}^{\mathrm{2}}& s[\mathit{\alpha },\mathit{\beta }]\\ s[\mathit{\beta },\mathit{\gamma }]& s[\mathit{\beta },t]& s[\mathit{\beta },\mathit{\alpha }]& s[\mathit{\beta }{]}^{\mathrm{2}}\end{array}\right]=\\ & -{\left[\begin{array}{cccc}\frac{{\partial }^{\mathrm{2}}\mathcal{L}}{\partial {\mathit{\gamma }}^{\mathrm{2}}}& \frac{{\partial }^{\mathrm{2}}\mathcal{L}}{\partial \mathit{\gamma }\partial t}& \frac{{\partial }^{\mathrm{2}}\mathcal{L}}{\partial \mathit{\gamma }\partial \mathit{\alpha }}& \frac{{\partial }^{\mathrm{2}}\mathcal{L}}{\partial \mathit{\gamma }\partial \mathit{\beta }}\\ \frac{{\partial }^{\mathrm{2}}\mathcal{L}}{\partial t\partial \mathit{\gamma }}& \frac{{\partial }^{\mathrm{2}}\mathcal{L}}{\partial t^{\mathrm{2}}}& \frac{{\partial }^{\mathrm{2}}\mathcal{L}}{\partial t\partial \mathit{\alpha }}& \frac{{\partial }^{\mathrm{2}}\mathcal{L}}{\partial t\partial \mathit{\beta }}\\ \frac{{\partial }^{\mathrm{2}}\mathcal{L}}{\partial \mathit{\alpha }\partial \mathit{\gamma }}& \frac{{\partial }^{\mathrm{2}}\mathcal{L}}{\partial \mathit{\alpha }\partial t}& \frac{{\partial }^{\mathrm{2}}\mathcal{L}}{\partial {\mathit{\alpha }}^{\mathrm{2}}}& \frac{{\partial }^{\mathrm{2}}\mathcal{L}}{\partial \mathit{\alpha }\partial \mathit{\beta }}\\ \frac{{\partial }^{\mathrm{2}}\mathcal{L}}{\partial \mathit{\beta }\partial \mathit{\gamma }}& \frac{{\partial }^{\mathrm{2}}\mathcal{L}}{\partial \mathit{\beta }\partial t}& \frac{{\partial }^{\mathrm{2}}\mathcal{L}}{\partial \mathit{\beta }\partial \mathit{\alpha }}& \frac{{\partial }^{\mathrm{2}}\mathcal{L}}{\partial {\mathit{\beta }}^{\mathrm{2}}}\end{array}\right]}^{-\mathrm{1}},\end{array}\end{array}$$

where Σ_γ is an n×n matrix; s[γ,t], s[γ,α] and s[γ,β] are n-element row vectors, s[t,γ], s[α,γ] and s[β,γ] are n-element column vectors, and all other elements are scalars. The second derivatives are given in Appendix C. The Fisher information matrix is best solved by block matrix inversion. This is achieved by partitioning Eq. (17) into four parts, with ${\partial }^{\mathrm{2}}\mathcal{L}/\partial {\mathit{\gamma }}^{\mathrm{2}}$ defining the first block.

If analytical uncertainty is the only source of data scatter around the discordia line, then the sum of squares S follows a central χ² distribution with 2n−3 degrees of freedom (i.e., ${\mathit{\chi }}_{\mathrm{2}n-\mathrm{3}}^{\mathrm{2}}$). Normalising S by the degrees of freedom gives rise to the so-called reduced χ² statistic, which is also known as the mean square of the weighted deviates (MSWD):

$$\begin{array}{}\text{(18)}& \text{MSWD}={\displaystyle \frac{S}{\mathrm{2}n-\mathrm{3}}}.\end{array}$$

Datasets are said to be overdispersed if S is greater than the 95 % percentile of ${\mathit{\chi }}_{\mathrm{2}n-\mathrm{3}}^{\mathrm{2}}$ or, equivalently, if MSWD≫1 Wendt and Carl (1991). The overdispersion can either be attributed to geological scatter in the concordia intercept age t, or to excess variability in the common Pb ratios α and β. Suppose that the scatter follows a normal distribution with zero mean and let ω be the standard deviation of this distribution. Then we can redefine Eq. (15) as

$$\begin{array}{}\text{(19)}& {\mathbf{\Sigma }}_{\mathrm{\Delta }}=\left[\begin{array}{cc}{\mathbf{J}}_x& {\mathbf{J}}_{\mathit{\lambda }}\end{array}\right]\left[\begin{array}{cc}{\mathbf{\Sigma }}_x& {\mathrm{0}}_{\mathrm{4}n\times \mathrm{4}}\\ {\mathrm{0}}_{\mathrm{4}\times \mathrm{4}n}& {\mathbf{\Sigma }}_{\mathit{\lambda }}\end{array}\right]\left[\begin{array}{c}{\mathbf{J}}_x^{\text{T}}\\ {\mathbf{J}}_{\mathit{\lambda }}^{\text{T}}\end{array}\right]+{\mathbf{J}}_{\mathit{\omega }}{\mathit{\omega }}^{\mathrm{2}}{\mathbf{J}}_{\mathit{\omega }}^{\text{T}},\end{array}$$

where J_ω is the Jacobian matrix with the partial derivatives of Δ with respect to the dispersion parameter ω. If the overdispersion is attributed to diachronous isotopic closure, then

$$\begin{array}{}\text{(20)}& {\mathbf{J}}_{\mathit{\omega }}=\left[\begin{array}{c}-{\mathit{\lambda }}_{\mathrm{35}}{e}^{{\mathit{\lambda }}_{\mathrm{35}}t}{I}_{n\times n}\\ -{\mathit{\lambda }}_{\mathrm{38}}{e}^{{\mathit{\lambda }}_{\mathrm{38}}t}{I}_{n\times n}\\ -{\mathit{\lambda }}_{\mathrm{32}}{e}^{{\mathit{\lambda }}_{\mathrm{32}}t}{I}_{n\times n}\end{array}\right],\end{array}$$

where I_n×n is the n×n identity matrix.

Alternatively, if the overdispersion is attributed to excess scatter of the common Pb ratios, then

$${\mathbf{J}}_{\mathit{\omega }}=\left[\begin{array}{c}-U\mathbf{W}\mathit{\gamma }\\ -\mathbf{W}\mathit{\gamma }\\ {\mathrm{0}}_{n\times \mathrm{1}}\end{array}\right].$$

ω can then be found by plugging Eq. (19) into Eq. (16) and maximising ℒ. Like before, the uncertainty of ω is obtained by inverting the Fisher information matrix, replacing Eq. (17) with

$$\begin{array}{}\text{(21)}& \begin{array}{rl}& \left[\begin{array}{ccccc}{\mathbf{\Sigma }}_{\mathit{\gamma }}& s[\mathit{\gamma },t]& s[\mathit{\gamma },\mathit{\alpha }]& s[\mathit{\gamma },\mathit{\beta }]& s[\mathit{\gamma },\mathit{\omega }]\\ s[t,\mathit{\gamma }]& s[t{]}^{\mathrm{2}}& s[t,\mathit{\alpha }]& s[t,\mathit{\beta }]& s[t,\mathit{\omega }]\\ s[\mathit{\alpha },\mathit{\gamma }]& s[\mathit{\alpha },t]& s[\mathit{\alpha }{]}^{\mathrm{2}}& s[\mathit{\alpha },\mathit{\beta }]& s[\mathit{\alpha },\mathit{\omega }]\\ s[\mathit{\beta },\mathit{\gamma }]& s[\mathit{\beta },t]& s[\mathit{\beta },\mathit{\alpha }]& s[\mathit{\beta }{]}^{\mathrm{2}}& s[\mathit{\beta },\mathit{\omega }]\\ s[\mathit{\omega },\mathit{\gamma }]& s[\mathit{\omega },t]& s[\mathit{\omega },\mathit{\alpha }]& s[\mathit{\omega },\mathit{\beta }{]}^{\mathrm{2}}& s[\mathit{\omega }{]}^{\mathrm{2}}\end{array}\right]=\\ & -{\left[\begin{array}{ccccc}\frac{{\partial }^{\mathrm{2}}\mathcal{L}}{\partial {\mathit{\gamma }}^{\mathrm{2}}}& \frac{{\partial }^{\mathrm{2}}\mathcal{L}}{\partial \mathit{\gamma }\partial t}& \frac{{\partial }^{\mathrm{2}}\mathcal{L}}{\partial \mathit{\gamma }\partial \mathit{\alpha }}& \frac{{\partial }^{\mathrm{2}}\mathcal{L}}{\partial \mathit{\gamma }\partial \mathit{\beta }}& \frac{{\partial }^{\mathrm{2}}\mathcal{L}}{\partial \mathit{\gamma }\partial \mathit{\omega }}\\ \frac{{\partial }^{\mathrm{2}}\mathcal{L}}{\partial t\partial \mathit{\gamma }}& \frac{{\partial }^{\mathrm{2}}\mathcal{L}}{\partial t^{\mathrm{2}}}& \frac{{\partial }^{\mathrm{2}}\mathcal{L}}{\partial t\partial \mathit{\alpha }}& \frac{{\partial }^{\mathrm{2}}\mathcal{L}}{\partial t\partial \mathit{\beta }}& \frac{{\partial }^{\mathrm{2}}\mathcal{L}}{\partial t\partial \mathit{\omega }}\\ \frac{{\partial }^{\mathrm{2}}\mathcal{L}}{\partial \mathit{\alpha }\partial \mathit{\gamma }}& \frac{{\partial }^{\mathrm{2}}\mathcal{L}}{\partial \mathit{\alpha }\partial t}& \frac{{\partial }^{\mathrm{2}}\mathcal{L}}{\partial {\mathit{\alpha }}^{\mathrm{2}}}& \frac{{\partial }^{\mathrm{2}}\mathcal{L}}{\partial \mathit{\alpha }\partial \mathit{\beta }}& \frac{{\partial }^{\mathrm{2}}\mathcal{L}}{\partial \mathit{\alpha }\partial \mathit{\omega }}\\ \frac{{\partial }^{\mathrm{2}}\mathcal{L}}{\partial \mathit{\beta }\partial \mathit{\gamma }}& \frac{{\partial }^{\mathrm{2}}\mathcal{L}}{\partial \mathit{\beta }\partial t}& \frac{{\partial }^{\mathrm{2}}\mathcal{L}}{\partial \mathit{\beta }\partial \mathit{\alpha }}& \frac{{\partial }^{\mathrm{2}}\mathcal{L}}{\partial {\mathit{\beta }}^{\mathrm{2}}}& \frac{{\partial }^{\mathrm{2}}\mathcal{L}}{\partial \mathit{\beta }\partial \mathit{\omega }}\\ \frac{{\partial }^{\mathrm{2}}\mathcal{L}}{\partial \mathit{\omega }\partial \mathit{\gamma }}& \frac{{\partial }^{\mathrm{2}}\mathcal{L}}{\partial \mathit{\omega }\partial t}& \frac{{\partial }^{\mathrm{2}}\mathcal{L}}{\partial \mathit{\omega }\partial \mathit{\alpha }}& \frac{{\partial }^{\mathrm{2}}\mathcal{L}}{\partial \mathit{\omega }\partial {\mathit{\beta }}^{\mathrm{2}}}& \frac{{\partial }^{\mathrm{2}}\mathcal{L}}{\partial {\mathit{\omega }}^{\mathrm{2}}}\end{array}\right]}^{-\mathrm{1}}.\end{array}\end{array}$$

In this case, manual calculation of the second derivatives is only possible if the overdispersion is attributed to t, with formulae shown in Appendix D. The second derivates are not tractable if the excess dispersion is assigned to α and β. In this case, the Fisher information matrix must always be calculated numerically, which can be difficult.

4 Application to literature data

This section applies the U–Th–Pb isochron algorithm to two published datasets: a carbonate dataset of Parrish et al. (2018) and an allanite dataset of Janots and Rubatto (2014). Parrish et al. (2018) investigated the Palaeogene deformation history of southern England by dating calcite veins in chalk and greensand. The measurements were made by quadrupole LA-ICP-MS, for which it was not possible to measure ²⁰⁴Pb with sufficient precision or accuracy. Figure 2a shows the U–Pb data of one particular sample (CB-2, Isle of Wight) on a conventional Tera–Wasserburg diagram. In the absence of ²⁰⁴Pb, conventional data processing would apply a common Pb correction using the ²⁰⁷Pb-method. That is, it would infer the concordia intercept age by regression of a semitotal-Pb∕U isochron. Doing so suggests a U–Pb age of 29.72±1.23 Myr. However, this isochron exhibits significant overdispersion with respect to the analytical uncertainties (MSWD of 3.2), casting doubt on the accuracy of the date. The fit also suffers from low precision, caused by the large uncertainties of the ²⁰⁷Pb-measurements. These cause the error ellipses of some spots to cross over into negative ²⁰⁷Pb ∕²⁰⁶Pb space.

The Th∕U ratios of CB-2 are extremely low (< .12, as shown on the colour scale of Fig. 2). These low ratios are caused by the low solubility of Th in the vein-forming fluids. As a consequence, less than 1 % of the measured ²⁰⁸Pb is of radiogenic origin. At the same time, the sample contains between 2 and 20 times more ²⁰⁸Pb than it does ²⁰⁷Pb. This makes the ²⁰⁸Pb-based $\mathrm{total}-\mathrm{Pb}/\mathrm{U}-\mathrm{Th}$ correction far more precise than the conventional ²⁰⁷Pb-based semitotal-Pb∕U correction. Figure 2b shows the $\mathrm{total}-\mathrm{Pb}/\mathrm{U}-\mathrm{Th}$ isochron of CB-2 in ²⁰⁸Pb_c ∕²⁰⁶Pb–²³⁸U ∕²⁰⁶Pb space. The scatter around this line is much tighter than that of the semitotal-Pb∕U fit, and the MSWD is only 2.5 despite the high precision of the added ²⁰⁸Pb data. The isochron intercept age has dropped to 24.43±0.84 Myr, which is significantly younger than the ²⁰⁷Pb-corrected date. Importantly, the two age estimates do not overlap within the stated uncertainties. The new date is close to, but not quite as young as, the 22.6±1.5 Myr value proposed by Parrish et al. (2018), which was obtained by a heuristic version of the $\mathrm{total}-\mathrm{Pb}/\mathrm{U}-\mathrm{Th}$ isochron algorithm.

It is not possible to formally prove that the ²⁰⁸Pb-corrected date is more accurate than the ²⁰⁷Pb-corrected date for the carbonate dataset. However, an independent assessment of accuracy is possible for our second case study. Janots and Rubatto (2014)'s allanite dataset used SIMS instead of LA-ICP-MS, making it possible to compare a ²⁰⁴Pb-based common Pb correction with the new ²⁰⁸Pb method. Figure 3a shows the U–Pb data of one particular allanite sample (MF482) on a conventional Tera–Wasserburg concordia diagram, yielding a semitotal-Pb∕U isochron age of 22.77±5.63 Myr. This is nearly identical to Janots and Rubatto (2014)'s ²⁰⁷Pb-corrected ²⁰⁸Pb ∕²⁰⁶Pb_c–²³²Th ∕²⁰⁶Pb_c isochron age of 22.7±1.0 Myr. As before, the Th∕U ratios are shown as shades of green to red. These values range from 23 to 235, which is 3 orders of magnitude higher than Parrish et al. (2018)'s carbonate data. Consequently, most of the chronometric power of the allanite data is contained in the Th–Pb system and not in the U–Pb method. 90 %–97 % of the ²⁰⁸Pb is radiogenic, as opposed to 0.3 %–1.0 % of the ²⁰⁶Pb, and only 0.06 %–0.016 % of the ²⁰⁷Pb.

Figure 3b shows the Th–Pb data in ²⁰⁴Pb ∕²⁰⁸Pb–²³²Th ∕²⁰⁸Pb space, where they form an isochron with a Th–Pb age of 21.50±4.37 Myr. This agrees within error with the ²⁰⁷Pb-corrected U–Pb age, despite the possible presence of an unresolved isobaric interference on ²⁰⁴Pb (Janots and Rubatto, 2014). However, the Th–Pb isochron age has a slightly smaller uncertainty and a much lower MSWD (0.74 instead of 1.4). Combining the U–Pb and Th–Pb systems together, Fig. 3c shows allanite sample MF482 in ²⁰⁸Pb_c ∕²⁰⁶Pb–²³⁸U ∕²⁰⁶Pb space, where it defines an 23.21±0.85 Myr isochron. This falls within the uncertainties of the U–Pb and Th–Pb age estimates but is more than 5 times more precise than the previous age estimates. An alternative visualisation of the $\mathrm{total}-\mathrm{Pb}/\mathrm{U}-\mathrm{Th}$ isochron is shown in Fig. 3d. Here, the ²⁰⁷Pb_c ∕²⁰⁸Pb ratio is plotted against ²³²Th ∕²⁰⁸Pb. Thus, we use the ²⁰⁷Pb as a common Pb indicator instead of the ²⁰⁴Pb used in Fig. 3b. The > 15 times greater abundance of ²⁰⁷Pb compared to ²⁰⁴Pb nearly quadruples the precision of the data, producing a tight fit around the isochron.

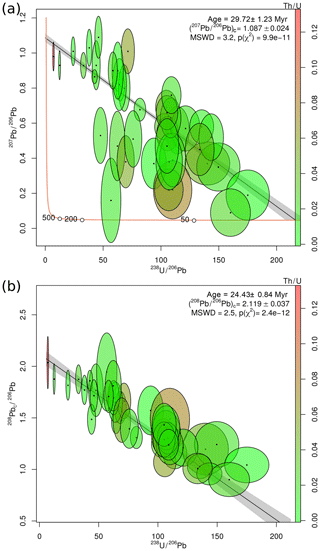
Figure 2 (a) Semitotal-Pb∕U isochron (²⁰⁷Pb-based common Pb correction) for Parrish et al. (2018)'s chalk data; (b) $\mathrm{total}-\mathrm{Pb}/\mathrm{U}-\mathrm{Th}$ isochron (²⁰⁸Pb-based common Pb correction) shown in ²⁰⁸Pb_c ∕²⁰⁶Pb–²³⁸U ∕²⁰⁶Pb space. Colours indicate the Th∕U ratio. All uncertainties are shown at 1σ.

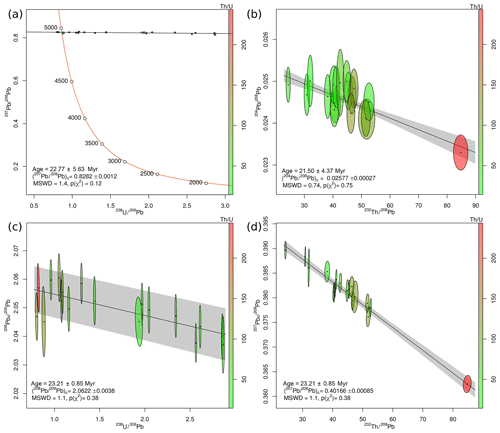
Figure 3 (a) Semitotal-Pb∕U isochron (²⁰⁷Pb-based common Pb correction) for Janots and Rubatto (2014)'s allanite data; (b) conventional Pb∕Th isochron (²⁰⁴Pb-based common Pb correction); (c, d) $\mathrm{total}-\mathrm{Pb}/\mathrm{U}-\mathrm{Th}$ isochron (²⁰⁸Pb-based common Pb correction) shown in ²⁰⁸Pb_c ∕²⁰⁶Pb–²³⁸U ∕²⁰⁶Pb space (c) and ²⁰⁶Pb_c ∕²⁰⁸Pb–²³²Th ∕²⁰⁸Pb space (d). Colours indicate the Th∕U ratio. All uncertainties are shown at 1σ.

5 Dealing with skewed error distributions

All the free parameters in the regression algorithm (t, α, β and ω) are strictly positive quantities. This positivity constraint manifests itself in skewed error distributions. For example, when the four parameter algorithm of Sect. 3 is applied to datasets that exhibit little or no overdispersion (ω≈0), then the usual 2σ error bounds can cross over into physically impossible negative data space. This section of the paper introduces two ways to deal with this problem.

A first solution is to obtain asymmetric uncertainty bounds for ω using a profile likelihood approach (Galbraith, 2005; Vermeesch, 2018). First, maximise Eq. (16) for the four parameters t, α, β and ω. Denote the corresponding log-likelihood value by ℒ_m. Second, consider a range of values for ω around the maximum likelihood estimate. For each of these values, maximise ℒ for t, α and β whilst keeping ω fixed. Denote the corresponding log likelihood by ℒ_ω. Finally, a 95 % confidence region for ω is obtained by collecting all the values of ω for which ${\mathcal{L}}_{\mathit{\omega }}>{\mathcal{L}}_{\text{m}}-\mathrm{3.85}/\mathrm{2}$, where 3.85 corresponds to the 95th percentile of a χ² distribution with one degree of freedom (Fig. 4). The same procedure can also be applied to t, α and β, in order to obtain asymmetric confidence intervals for those parameters if needed. This would be particularly useful for very young samples.

A second and more pragmatic approach to dealing with the positivity constraint is to simply redefine the regression parameters in terms of logarithmic quantities. This is done by replacing Eqs. (11), (12) and (19) with

$$\begin{array}{ll}\text{(22)}& {\displaystyle }\mathit{K}=& {\displaystyle }\mathit{X}-U\exp \left[{\mathit{\beta }}_{\ast }\right]\mathbf{W}\mathit{\gamma }-\exp \left[{\mathit{\lambda }}_{\mathrm{35}}{e}^{t_{\ast }}\right]+\mathrm{1}\text{(23)}& {\displaystyle }\mathit{L}=& {\displaystyle }\mathit{Y}-\exp \left[{\mathit{\alpha }}_{\ast }\right]\mathbf{W}\mathit{\gamma }-\exp \left[{\mathit{\lambda }}_{\mathrm{38}}{e}^{t_{\ast }}\right]+\mathrm{1}\text{(24)}& {\displaystyle }{\mathbf{\Sigma }}_{\mathrm{\Delta }}=& {\displaystyle }\left[\begin{array}{cc}{\mathbf{J}}_x& {\mathbf{J}}_{\mathit{\lambda }}\end{array}\right]\left[\begin{array}{cc}{\mathbf{\Sigma }}_x& {\mathrm{0}}_{\mathrm{4}n\times \mathrm{4}}\\ {\mathrm{0}}_{\mathrm{4}\times \mathrm{4}n}& {\mathbf{\Sigma }}_{\mathit{\lambda }}\end{array}\right]\left[\begin{array}{c}{\mathbf{J}}_x^{\text{T}}\\ {\mathbf{J}}_{\mathit{\lambda }}^{\text{T}}\end{array}\right]{\displaystyle }& {\displaystyle }+{\mathbf{J}}_{\mathit{\omega }}\exp [{\mathit{\omega }}_{\ast }{]}^{\mathrm{2}}{\mathbf{J}}_{\mathit{\omega }}^{\text{T}},\end{array}$$

respectively, and maximising Eq. (16) with respect to t_∗, α_∗, β_∗ and ω_∗. The standard errors for these log parameters (again obtained from the Fisher information matrix) can then be converted to asymmetric confidence intervals for t, α, β and ω. This approach yields results that are similar to those obtained using the profile log-likelihood method, as illustrated in Fig. 4 for monazite grain no. 10 in sample BHE-01 of Gibson et al. (2016). This sample experienced a diachronous crystallisation history, resulting in an overdispersed $\mathrm{total}-\mathrm{Pb}/\mathrm{U}-\mathrm{Th}$ isochron fit (MSWD of 8). Quantifying the excess dispersion with a model-3 fit yields an overdispersion parameter ω=0.67 Myr with asymmetric confidence bounds of +0.48/−0.23 Myr. Besides generating realistic confidence regions, the logarithmic re-parameterisation of the likelihood function has the added benefit increasing the numerical stability of the maximum likelihood method.

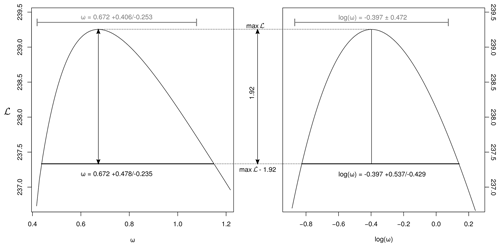
Figure 4 Profile log-likelihood intervals of the overdispersion parameter ω (black, left) and log (ω) (black, right) for the Gibson et al. (2016) dataset. The set of ω values whose log likelihoods fall within a range of 1.92 from the maximum value defines an asymmetric 95 % confidence interval. Alternatively, a standard symmetric confidence interval for log (ω) (grey, right) can be mapped to an asymmetric confidence interval for ω (grey, left). The two approaches yield similar results.

6 Detrital samples

So far, we have assumed that all the U–Th–Pb measurements are cogenetic and share the same common Pb composition. This assumption is generally not valid for detrital minerals, which tend to contain a mixture of provenance components. In this case the different crystals in a sample are not expected to plot along a single isochron line. However, it is still possible to remove the common Pb component by making certain assumptions about its composition. One way to do this is to assume that the mineral of interest was extracted from a reservoir of known U–Th–Pb composition.

For example, using the two-stage Pb evolution model of Stacey and Kramers (1975), it is possible to predict the ²⁰⁶Pb ∕²⁰⁸Pb and ²⁰⁷Pb ∕²⁰⁸Pb ratios of the reservoir for any given time t. More specifically, if t<3.7 Ga, then

$$\begin{array}{}\text{(25)}& {\displaystyle }& {\displaystyle }\mathit{\alpha }\left(t\right)={\displaystyle \frac{{\left[\frac{{}^{\mathrm{206}}\mathrm{Pb}}{{}^{\mathrm{204}}\mathrm{Pb}}\right]}_{\mathrm{3.7}}+{\left[\frac{{}^{\mathrm{238}}\mathrm{U}}{{}^{\mathrm{204}}\mathrm{Pb}}\right]}_{sk}\left(e^{{\mathit{\lambda }}_{\mathrm{38}}\mathrm{3.7}}-e^{{\mathit{\lambda }}_{\mathrm{38}}t}\right)}{{\left[\frac{{}^{\mathrm{208}}\mathrm{Pb}}{{}^{\mathrm{204}}\mathrm{Pb}}\right]}_{\mathrm{3.7}}+{\left[\frac{{}^{\mathrm{232}}\mathrm{Th}}{{}^{\mathrm{204}}\mathrm{Pb}}\right]}_{sk}\left(e^{{\mathit{\lambda }}_{\mathrm{32}}\mathrm{3.7}}-e^{{\mathit{\lambda }}_{\mathrm{32}}t}\right)}}\text{(26)}& {\displaystyle }& {\displaystyle }\mathit{\beta }\left(t\right)={\displaystyle \frac{{\left[\frac{{}^{\mathrm{207}}\mathrm{Pb}}{{}^{\mathrm{204}}\mathrm{Pb}}\right]}_{\mathrm{3.7}}+\frac{\mathrm{1}}{U}{\left[\frac{{}^{\mathrm{238}}\mathrm{U}}{{}^{\mathrm{204}}\mathrm{Pb}}\right]}_{sk}\left(e^{{\mathit{\lambda }}_{\mathrm{35}}\mathrm{3.7}}-e^{{\mathit{\lambda }}_{\mathrm{35}}t}\right)}{{\left[\frac{{}^{\mathrm{208}}\mathrm{Pb}}{{}^{\mathrm{204}}\mathrm{Pb}}\right]}_{\mathrm{3.7}}+{\left[\frac{{}^{\mathrm{232}}\mathrm{Th}}{{}^{\mathrm{204}}\mathrm{Pb}}\right]}_{sk}\left(e^{{\mathit{\lambda }}_{\mathrm{32}}\mathrm{3.7}}-e^{{\mathit{\lambda }}_{\mathrm{32}}t}\right)}},\end{array}$$

where

$$\begin{array}{rl}& {\left[{\displaystyle \frac{{}^{\mathrm{206}}\mathrm{Pb}}{{}^{\mathrm{204}}\mathrm{Pb}}}\right]}_{\mathrm{3.7}}=\mathrm{11.152},{\left[{\displaystyle \frac{{}^{\mathrm{208}}\mathrm{Pb}}{{}^{\mathrm{204}}\mathrm{Pb}}}\right]}_{\mathrm{3.7}}=\mathrm{31.23},\\ & {\left[{\displaystyle \frac{{}^{\mathrm{207}}\mathrm{Pb}}{{}^{\mathrm{204}}\mathrm{Pb}}}\right]}_{\mathrm{3.7}}=\mathrm{12.998},{\left[{\displaystyle \frac{{}^{\mathrm{238}}\mathrm{U}}{{}^{\mathrm{204}}\mathrm{Pb}}}\right]}_{sk}=\mathrm{9.74},\end{array}$$

and

$${\left[{\displaystyle \frac{{}^{\mathrm{232}}\mathrm{Th}}{{}^{\mathrm{204}}\mathrm{Pb}}}\right]}_{sk}=\mathrm{36.84}.$$

Substituting α(t) and β(t) for α and β in Eqs. (11)–(13) reduces the number of free parameters from three (α, β and t) to one (t). This provides a quick and numerically robust mechanism for common Pb correction of detrital minerals. It is the maximum likelihood equivalent of the heuristic approach used by Chew et al. (2011).

7 Implementation in IsoplotR

The algorithms presented in this paper have been implemented in the IsoplotR software toolbox for geochronology (Vermeesch, 2018). The easiest way to use the U–Th–Pb isochron functions is via an online graphical user interface at http://isoplotr.london-geochron.com (last access: 4 May 2020). Alternatively, the same functions can also be accessed from the command line, using the R programming language (R Core Team, 2020). This section of the paper presents some code snippets to illustrate the key functions involved. This brief tutorial assumes that the reader has R and IsoplotR installed on her/his computer. Further details about this are provided by Vermeesch (2018) and on the aforementioned website. First, we need to load IsoplotR into R:

library(IsoplotR)

Two new data formats have been added to IsoplotR's existing six U–Pb formats, to accommodate datasets comprising ²³²Th and ²⁰⁸Pb. Sample Ga2 of Janots and Rubatto (2014) has been included in the IsoplotR package as two data files (UPb7.csv and UPb8.csv).

UPb7.csv specifies the U–Th–Pb composition using the Wetherill ratios ²⁰⁷Pb ∕²³⁵U, ²⁰⁶Pb ∕²³⁸U, ²⁰⁸Pb ∕²³²Th and ²³²Th ∕²³⁸U, whereas UPb8.csv uses the Tera–Wasserburg ratios ²³⁸U ∕²⁰⁶Pb, ²⁰⁷Pb ∕²⁰⁶Pb, ²⁰⁸Pb ∕²⁰⁶Pb and ²³²Th ∕²³⁸U. The key difference between the two formats is the strength of the internal error correlations, which is greater for format 7 than it is for format 8. The following commands load the contents of UPb8.csv into a variable called UPb and plot the data on a ²⁰⁸Pb ∕²³²Th vs. ²⁰⁶Pb ∕²³⁸U-concordia diagram:

Performing a discordia regression and visualising the results as a ²⁰⁸Pb_c ∕²⁰⁶Pb vs. ²³⁸U ∕²⁰⁶Pb isochron:

isochron(UPb,type=1)

which performs a three-parameter regression without overdispersion. Accounting for overdispersion is done using the optional model argument:

fit <- isochron(UPb,type=1,model=3)

where fit is a variable that stores the numerical results of the isochron regression. This is a list of items that can be inspected by typing fit at the R command prompt. For example, the maximum likelihood estimates for t, α, β and ω are stored in fit$par and the covariance matrix in fit$cov. Changing type to 2 plots the regression results as a ²⁰⁸Pb_c ∕²⁰⁷Pb vs. ²³⁵U ∕²⁰⁷Pb isochron. The isochron results can also be visualised on the concordia diagram:

concordia(UPb,type=2,show.age=2)

where type=2 produces a Tera–Wasserburg diagram and the show.age argument adds a three-parameter regression line to it. Change this to show.age=4 for a four-parameter fit.

8 Discussion and future developments

This paper introduced a $\mathrm{total}-\mathrm{Pb}/\mathrm{U}-\mathrm{Th}$ algorithm for common Pb correction by joint regression of all Pb isotopes of U and Th. For samples that are low in Th (such as carbonates), ²⁰⁸Pb offers the most precise way to correct for common Pb, because ²⁰⁸Pb tends to be more abundant than both ²⁰⁴Pb and ²⁰⁷Pb. For samples that are high in Th, the ²⁰⁸Pb ∕²³²Th clock adds chronometrically valuable information to the joint U–Pb decay systems.

The ingrowth of radiogenic Pb described by Eqs. (2)–(4) assumes initial secular equilibrium between all the intermediate daughters in the U–Th–Pb decay chains. The new discordia regression algorithm can be modified to accommodate departures from this assumption. In fact, such disequilibrium corrections have already been implemented in IsoplotR, using the matrix derivative approach of McLean et al. (2016). A paper detailing these calculations is in preparation by the latter author. The disequilibrium correction is particularly useful for applications to young carbonates, whose initial ²³⁴U ∕²³⁸U and ²³⁰Th ∕²³⁸U activity ratios may be far out of equilibrium.

The new discordia regression algorithm is based on the method of maximum likelihood and accounts for correlated uncertainties between variables. However, geochronological datasets are often associated with equally significant error correlations between samples (Vermeesch, 2015). The algorithm presented in this paper easily handles such correlations, which carry systematic uncertainty. These are represented by the off-diagonal terms of the covariance matrix Σ_x in Eq. (15). However, to use this option in practical applications will require a new generation of low-level data processing software.

This new-generation software will also need to deal with a second issue that negatively affects the accuracy of the U(–Th)–Pb method, which is apparent from Fig. 1. After removing the radiogenic ²⁰⁸Pb component from the Janots and Rubatto (2014) dataset, the 95 % confidence ellipse of one of the aliquots crosses over into negative ²⁰⁸Pb ∕²³²Th ratios. This nonsensical result is related to the issues discussed in Sect. 5. Isotopic data are strictly positive quantities that exhibit skewed error distributions. “Normal” statistical operations such as averaging and the calculation of 2σ confidence intervals can produce counterintuitive results when applied to such data.

In Sect. 5, the skewness of the fit parameters was removed by reformulating the regression algorithm in terms of logarithmic quantities. Similarly, Vermeesch (2015) showed that the skewness of isotopic compositions can be removed using log ratios, in the context of ⁴⁰Ar ∕³⁹Ar geochronology. McLean et al. (2016) introduced the same approach to in situ U–Pb geochronology by LA-ICP-MS. Future software development will allow analysts to export their U–Th–Pb isotopic data directly as log ratios and covariance matrices. Such a data structure can still be analysed with the new discordia regression algorithm, after a logarithmic change a variables for X, Y, Z and W in Eqs. (11), (12) and (13).

The U–Pb method is one of the most powerful and versatile methods in the geochronological toolbox. With two isotopes of the same parent (²³⁵U and ²³⁸U) decaying to two different isotopes of the same daughter (²⁰⁷Pb and ²⁰⁶Pb), the U–Pb method offers an internal quality control that is absent from most other geochronological techniques. U-bearing minerals often contain significant amounts of Th, which decays to ²⁰⁸Pb. However, until this day, geochronologists have not frequently used this additional parent–daughter pair to its full potential. It is hoped that the algorithm and software presented in this paper will change this situation.

Appendix A

The covariance matrix of the isotopic ratio measurements X, Y, Z and W is given by

$$\begin{array}{}\text{(A1)}& {\mathbf{\Sigma }}_x=\left[\begin{array}{cccc}{\mathbf{\Sigma }}_X& {\mathbf{\Sigma }}_{X,Y}& {\mathbf{\Sigma }}_{X,Z}& {\mathbf{\Sigma }}_{X,W}\\ {\mathbf{\Sigma }}_{Y,X}& {\mathbf{\Sigma }}_Y& {\mathbf{\Sigma }}_{Y,Z}& {\mathbf{\Sigma }}_{Y,W}\\ {\mathbf{\Sigma }}_{Z,X}& {\mathbf{\Sigma }}_{Z,Y}& {\mathbf{\Sigma }}_Z& {\mathbf{\Sigma }}_{Z,W}\\ {\mathbf{\Sigma }}_{W,X}& {\mathbf{\Sigma }}_{W,Y}& {\mathbf{\Sigma }}_{W,Z}& {\mathbf{\Sigma }}_W\end{array}\right],\end{array}$$

where

$$\begin{array}{}\text{(A2)}& {\mathbf{\Sigma }}_X=\left[\begin{array}{cccc}s[X_{\mathrm{1}}{]}^{\mathrm{2}}& s[X_{\mathrm{1}},X_{\mathrm{2}}]& \mathrm{\dots }& s[X_{\mathrm{1}},X_n]\\ s[X_{\mathrm{2}},X_{\mathrm{1}}]& s[X_{\mathrm{2}}{]}^{\mathrm{2}}& \mathrm{\dots }& s[X_{\mathrm{2}},X_n]\\ \mathrm{⋮}& \mathrm{⋮}& \mathrm{\ddots }& \mathrm{⋮}\\ s[X_n,X_{\mathrm{1}}]& s[X_n,X_{\mathrm{2}}]& \mathrm{\dots }& s[X_n{]}^{\mathrm{2}}\end{array}\right],\end{array}$$

$$\begin{array}{}\text{(A3)}& {\mathbf{\Sigma }}_{X,Y}=\left[\begin{array}{cccc}s[X_{\mathrm{1}},Y_{\mathrm{1}}{]}^{\mathrm{2}}& s[X_{\mathrm{1}},Y_{\mathrm{2}}]& \mathrm{\dots }& s[X_{\mathrm{1}},Y_n]\\ s[X_{\mathrm{2}},Y_{\mathrm{1}}]& s[X_{\mathrm{2}},Y_{\mathrm{2}}]& \mathrm{\dots }& s[X_{\mathrm{2}},Y_n]\\ \mathrm{⋮}& \mathrm{⋮}& \mathrm{\ddots }& \mathrm{⋮}\\ s[X_n,Y_{\mathrm{1}}]& s[X_n,Y_{\mathrm{2}}]& \mathrm{\dots }& s[X_n,Y_n]\end{array}\right],\end{array}$$

and so forth, in which s[a]² is the variance of a and s[a,b] is the covariance of a and b, for any a and b. Σ_λ is the covariance matrix of the decay constants and the ²³⁸U ∕²³⁵U ratio:

$$\begin{array}{}\text{(A4)}& {\mathbf{\Sigma }}_{\mathit{\lambda }}=\left[\begin{array}{cccc}s[{\mathit{\lambda }}_{\mathrm{35}}{]}^{\mathrm{2}}& \mathrm{0}& \mathrm{0}& \mathrm{0}\\ \mathrm{0}& s[{\mathit{\lambda }}_{\mathrm{38}}{]}^{\mathrm{2}}& \mathrm{0}& \mathrm{0}\\ \mathrm{0}& \mathrm{0}& s[{\mathit{\lambda }}_{\mathrm{32}}{]}^{\mathrm{2}}& \mathrm{0}\\ \mathrm{0}& \mathrm{0}& \mathrm{0}& s[U{]}^{\mathrm{2}}\end{array}\right],\end{array}$$

Here, the covariance terms have been set to zero, but nonzero values could also be accommodated. Finally, the Jacobian matrices J_x and J_λ are given by

$$\begin{array}{}\text{(A5)}& {\mathbf{J}}_x=\left[\begin{array}{cccc}{I}_{n\times n}& {\mathrm{0}}_{n\times n}& {\mathrm{0}}_{n\times n}& -U\mathit{\beta }{I}_{n\times n}\mathit{\gamma }\\ {\mathrm{0}}_{n\times n}& I_{n\times n}& {\mathrm{0}}_{n\times n}& -\mathit{\alpha }{I}_{n\times n}\mathit{\gamma }\\ {\mathrm{0}}_{n\times n}& {\mathrm{0}}_{n\times n}& I_{n\times n}& {\mathrm{0}}_{n\times n}\end{array}\right],\end{array}$$

and

$$\begin{array}{}\text{(A6)}& \begin{array}{rl}& {\mathbf{J}}_{\mathit{\lambda }}=\\ & \left[\begin{array}{cccc}-{\mathrm{1}}_{n\times \mathrm{1}}t{e}^{{\mathit{\lambda }}_{\mathrm{35}}t}& {\mathrm{0}}_{n\times \mathrm{1}}& {\mathrm{0}}_{n\times \mathrm{1}}& -\mathit{\beta }\mathbf{W}\mathit{\gamma }\\ {\mathrm{0}}_{n\times \mathrm{1}}& -{\mathrm{1}}_{n\times \mathrm{1}}t{e}^{{\mathit{\lambda }}_{\mathrm{38}}t}& {\mathrm{0}}_{n\times \mathrm{1}}& {\mathrm{0}}_{n\times \mathrm{1}}\\ {\mathrm{0}}_{n\times \mathrm{1}}& {\mathrm{0}}_{n\times \mathrm{1}}& -{\mathrm{1}}_{n\times \mathrm{1}}t{e}^{{\mathit{\lambda }}_{\mathrm{32}}t}& {\mathrm{0}}_{n\times \mathrm{1}}\end{array}\right],\end{array}\end{array}$$

where 1_n×1 is an n-element column vector of ones.

Appendix B

The numerical stability of the optimisation is greatly enhanced by dropping the dependency of the sum of squares S on the uncertainty of the Th∕U ratios W. Thus, we replace Eq. (A1) by

$$\begin{array}{}\text{(B1)}& {\mathbf{\Sigma }}_x=\left[\begin{array}{ccc}{\mathbf{\Sigma }}_X& {\mathbf{\Sigma }}_{X,Y}& {\mathbf{\Sigma }}_{X,Z}\\ {\mathbf{\Sigma }}_{Y,X}& {\mathbf{\Sigma }}_Y& {\mathbf{\Sigma }}_{Y,Z}\\ {\mathbf{\Sigma }}_{Z,X}& {\mathbf{\Sigma }}_{Z,Y}& {\mathbf{\Sigma }}_Z\end{array}\right],\end{array}$$

and Eq. (A5) by the 3n×3n identity matrix (i.e., ${\mathbf{J}}_x=I_{\mathrm{3}n\times \mathrm{3}n}$). Let us define Ω to be the inverse covariance matrix of Δ, so that

$$\begin{array}{}\text{(B2)}& {\mathbf{\Sigma }}_{\mathrm{\Delta }}^{-\mathrm{1}}\equiv \mathbf{\Omega }=\left[\begin{array}{ccc}{\mathbf{\Omega }}_{\mathrm{1},\mathrm{1}}& {\mathbf{\Omega }}_{\mathrm{1},\mathrm{2}}& {\mathbf{\Omega }}_{\mathrm{1},\mathrm{3}}\\ {\mathbf{\Omega }}_{\mathrm{2},\mathrm{1}}& {\mathbf{\Omega }}_{\mathrm{2},\mathrm{2}}& {\mathbf{\Omega }}_{\mathrm{2},\mathrm{3}}\\ {\mathbf{\Omega }}_{\mathrm{3},\mathrm{1}}& {\mathbf{\Omega }}_{\mathrm{3},\mathrm{2}}& {\mathbf{\Omega }}_{\mathrm{3},\mathrm{3}}\end{array}\right].\end{array}$$

Then, we can directly estimate γ for any given value of t, α and β, by replacing γ with $\mathit{Z}-\mathit{M}-e^{{\mathit{\lambda }}_{\mathrm{32}}t}+\mathrm{1}$ in Eq. (13), so that

$$\mathit{K}=\widehat{\mathit{K}}+U\mathit{\beta }\mathbf{W}\mathit{M}$$

with

$$\begin{array}{}\text{(B3)}& \widehat{\mathit{K}}=\mathit{X}-U\mathit{\beta }\mathbf{W}(\mathit{Z}-e^{{\mathit{\lambda }}_{\mathrm{32}}t}+\mathrm{1})-e^{{\mathit{\lambda }}_{\mathrm{35}}t}+\mathrm{1}\end{array}$$

and

$$\mathit{L}=\widehat{\mathit{L}}+\mathit{\alpha }\mathbf{W}\mathit{M}$$

with

$$\begin{array}{}\text{(B4)}& \widehat{\mathit{L}}=\mathit{Y}-\mathit{\alpha }\mathbf{W}(\mathit{Z}-e^{{\mathit{\lambda }}_{\mathrm{32}}t}+\mathrm{1})-e^{{\mathit{\lambda }}_{\mathrm{38}}t}+\mathrm{1}.\end{array}$$

Plugging Eqs. (B3) and (B4) into Eq. (14) and rearranging yields

$$\begin{array}{}\text{(B5)}& S={\mathit{M}}^{\text{T}}\mathbf{A}\mathit{M}+\mathbf{B}\mathit{M}+{\mathit{M}}^{\text{T}}\mathbf{C}+D,\end{array}$$

where

$$\begin{array}{}\text{(B6)}& {\displaystyle }\begin{array}{rl}\mathbf{A}=& U^{\mathrm{2}}{\mathit{\beta }}^{\mathrm{2}}{\mathbf{W}}_d{\mathbf{\Omega }}_{\mathrm{1},\mathrm{1}}{\mathbf{W}}_d+{\mathit{\alpha }}^{\mathrm{2}}{\mathbf{W}}_d{\mathbf{\Omega }}_{\mathrm{2},\mathrm{2}}{\mathbf{W}}_d+{\mathbf{\Omega }}_{\mathrm{3},\mathrm{3}}\\ & +U\mathit{\alpha }\mathit{\beta }{\mathbf{W}}_d({\mathbf{\Omega }}_{\mathrm{1},\mathrm{2}}+{\mathbf{\Omega }}_{\mathrm{2},\mathrm{1}}){\mathbf{W}}_d\\ & +U\mathit{\beta }({\mathbf{W}}_d{\mathbf{\Omega }}_{\mathrm{1},\mathrm{3}}+{\mathbf{\Omega }}_{\mathrm{3},\mathrm{1}}{\mathbf{W}}_d)\\ & +\mathit{\alpha }({\mathbf{W}}_d{\mathbf{\Omega }}_{\mathrm{2},\mathrm{3}}+{\mathbf{\Omega }}_{\mathrm{3},\mathrm{2}}{\mathbf{W}}_d)\end{array}\text{(B7)}& {\displaystyle }\begin{array}{rl}\mathbf{B}=& U\mathit{\beta }{\widehat{\mathit{K}}}^{\text{T}}{\mathbf{\Omega }}_{\mathrm{1},\mathrm{1}}{\mathbf{W}}_d+\mathit{\alpha }{\widehat{\mathit{L}}}^{\text{T}}{\mathbf{\Omega }}_{\mathrm{2},\mathrm{2}}{\mathbf{W}}_d+\mathit{\alpha }{\widehat{\mathit{K}}}^{\text{T}}{\mathbf{\Omega }}_{\mathrm{1},\mathrm{2}}{\mathbf{W}}_d\\ & +U\mathit{\beta }{\widehat{\mathit{L}}}^{\text{T}}{\mathbf{\Omega }}_{\mathrm{2},\mathrm{1}}{\mathbf{W}}_d+{\widehat{\mathit{K}}}^{\text{T}}{\mathbf{\Omega }}_{\mathrm{1},\mathrm{3}}+{\widehat{\mathit{L}}}^{\text{T}}{\mathbf{\Omega }}_{\mathrm{2},\mathrm{3}}\end{array}\text{(B8)}& {\displaystyle }\begin{array}{rl}\mathbf{C}=& U\mathit{\beta }{\mathbf{W}}_d{\mathbf{\Omega }}_{\mathrm{1},\mathrm{1}}\widehat{\mathit{K}}+\mathit{\alpha }{\mathbf{W}}_d{\mathbf{\Omega }}_{\mathrm{2},\mathrm{2}}\widehat{\mathit{L}}+U\mathit{\beta }{\mathbf{W}}_d{\mathbf{\Omega }}_{\mathrm{1},\mathrm{2}}\widehat{\mathit{L}}\\ & +\mathit{\alpha }{\mathbf{W}}_d{\mathbf{\Omega }}_{\mathrm{2},\mathrm{1}}\widehat{\mathit{K}}+{\mathbf{\Omega }}_{\mathrm{3},\mathrm{1}}\widehat{\mathit{K}}+{\mathbf{\Omega }}_{\mathrm{3},\mathrm{2}}\widehat{\mathit{L}}\end{array}\text{(B9)}& {\displaystyle }D={\widehat{\mathit{K}}}^{\text{T}}{\mathbf{\Omega }}_{\mathrm{1},\mathrm{1}}\widehat{\mathit{K}}+{\widehat{\mathit{K}}}^{\text{T}}{\mathbf{\Omega }}_{\mathrm{1},\mathrm{2}}\widehat{\mathit{L}}+{\widehat{\mathit{L}}}^{\text{T}}{\mathbf{\Omega }}_{\mathrm{2},\mathrm{1}}\widehat{\mathit{K}}+{\widehat{\mathit{L}}}^{\text{T}}{\mathbf{\Omega }}_{\mathrm{2},\mathrm{2}}\widehat{\mathit{L}}.\end{array}$$

Taking the matrix derivative of S with respect to M,

$$\begin{array}{}\text{(B10)}& \partial S/\partial \mathit{M}={\mathit{M}}^{\text{T}}(\mathbf{A}+{\mathbf{A}}^{\text{T}})+\mathbf{B}+{\mathbf{C}}^{\text{T}}.\end{array}$$

Setting $\partial S/\partial \mathit{M}=\mathrm{0}$ and solving for M,

$$\begin{array}{}\text{(B11)}& \mathit{M}=-(\mathbf{A}+{\mathbf{A}}^{\text{T}}{)}^{-\mathrm{1}}({\mathbf{B}}^{\text{T}}+\mathbf{C}).\end{array}$$

Plugging M back into Eq. (13) yields our estimate of γ, which allows us to calculate S. The values of t, α and β that minimise S are then found by numerical methods.

Appendix C

Explicit formulae for the Fisher information matrix (Eq. 17) are possible for the simplified algorithm, in which the uncertainty of W is ignored:

$$\begin{array}{}\text{(C1)}& {\displaystyle \frac{{\partial }^{\mathrm{2}}\mathcal{L}}{\partial {\mathit{\gamma }}^{\mathrm{2}}}}=-{\left[\begin{array}{c}U\mathit{\beta }\mathbf{W}\\ \mathit{\alpha }\mathbf{W}\\ I_{n\times n}\end{array}\right]}^{\text{T}}{\mathbf{\Sigma }}_{\mathrm{\Delta }}^{-\mathrm{1}}\left[\begin{array}{c}U\mathit{\beta }\mathbf{W}\\ \mathit{\alpha }\mathbf{W}\\ I_{n\times n}\end{array}\right]\end{array}$$

$$\begin{array}{}\text{(C2)}& \begin{array}{rl}& {\displaystyle \frac{{\partial }^{\mathrm{2}}\mathcal{L}}{\partial \mathit{\gamma }\partial t}}={\left({\displaystyle \frac{{\partial }^{\mathrm{2}}\mathcal{L}}{\partial t\partial \mathit{\gamma }}}\right)}^{\text{T}}=\\ & -{\left[\begin{array}{c}U\mathit{\beta }\mathbf{W}\\ \mathit{\alpha }\mathbf{W}\\ I_{n\times n}\end{array}\right]}^{\text{T}}{\mathbf{\Sigma }}_{\mathrm{\Delta }}^{-\mathrm{1}}\left[\begin{array}{c}({\mathit{\lambda }}_{\mathrm{35}}{e}^{{\mathit{\lambda }}_{\mathrm{35}}t}{)}_{n\times \mathrm{1}}\\ ({\mathit{\lambda }}_{\mathrm{38}}{e}^{{\mathit{\lambda }}_{\mathrm{38}}t}{)}_{n\times \mathrm{1}}\\ ({\mathit{\lambda }}_{\mathrm{32}}{e}^{{\mathit{\lambda }}_{\mathrm{32}}t}{)}_{n\times \mathrm{1}}\end{array}\right]\end{array}\end{array}$$

$$\begin{array}{}\text{(C3)}& \begin{array}{rl}& {\displaystyle \frac{{\partial }^{\mathrm{2}}\mathcal{L}}{\partial \mathit{\gamma }\partial \mathit{\alpha }}}={\left({\displaystyle \frac{{\partial }^{\mathrm{2}}\mathcal{L}}{\partial \mathit{\alpha }\partial \mathit{\gamma }}}\right)}^{\text{T}}=\\ & {\left[\begin{array}{c}{\mathrm{0}}_{n\times n}\\ \mathbf{W}\\ {\mathrm{0}}_{n\times n}\end{array}\right]}^{\text{T}}{\mathbf{\Sigma }}_{\mathrm{\Delta }}^{-\mathrm{1}}\mathbf{\Delta }-{\left[\begin{array}{c}U\mathit{\beta }\mathbf{W}\\ \mathit{\alpha }\mathbf{W}\\ I_{n\times n}\end{array}\right]}^{\text{T}}{\mathrm{\Sigma }}_{\mathrm{\Delta }}^{-\mathrm{1}}\left[\begin{array}{c}{\mathrm{0}}_{n\times \mathrm{1}}\\ \mathbf{W}\mathit{\gamma }\\ {\mathrm{0}}_{n\times \mathrm{1}}\end{array}\right]\end{array}\end{array}$$

$$\begin{array}{}\text{(C4)}& \begin{array}{rl}& {\displaystyle \frac{{\partial }^{\mathrm{2}}\mathcal{L}}{\partial \mathit{\gamma }\partial \mathit{\beta }}}={\left({\displaystyle \frac{{\partial }^{\mathrm{2}}\mathcal{L}}{\partial \mathit{\beta }\partial \mathit{\gamma }}}\right)}^{\text{T}}=\\ & {\left[\begin{array}{c}U\mathbf{W}\\ {\mathrm{0}}_{n\times n}\\ {\mathrm{0}}_{n\times n}\end{array}\right]}^{\text{T}}{\mathbf{\Sigma }}_{\mathrm{\Delta }}^{-\mathrm{1}}\mathbf{\Delta }-{\left[\begin{array}{c}U\mathit{\beta }\mathbf{W}\\ \mathit{\alpha }\mathbf{W}\\ I_{n\times n}\end{array}\right]}^{\text{T}}{\mathbf{\Sigma }}_{\mathrm{\Delta }}^{-\mathrm{1}}\left[\begin{array}{c}U\mathbf{W}\mathit{\gamma }\\ {\mathrm{0}}_{n\times \mathrm{1}}\\ {\mathrm{0}}_{n\times \mathrm{1}}\end{array}\right]\end{array}\end{array}$$

$$\begin{array}{}\text{(C5)}& \begin{array}{rl}{\displaystyle \frac{{\partial }^{\mathrm{2}}\mathcal{L}}{\partial t^{\mathrm{2}}}}=& {\mathbf{\Delta }}^{\text{T}}{\mathbf{\Sigma }}_{\mathrm{\Delta }}^{-\mathrm{1}}\left[\begin{array}{c}(e^{{\mathit{\lambda }}_{\mathrm{35}}t}{\mathit{\lambda }}_{\mathrm{35}}^{\mathrm{2}}{)}_{n\times \mathrm{1}}\\ (e^{{\mathit{\lambda }}_{\mathrm{38}}t}{\mathit{\lambda }}_{\mathrm{38}}^{\mathrm{2}}{)}_{n\times \mathrm{1}}\\ (e^{{\mathit{\lambda }}_{\mathrm{32}}t}{\mathit{\lambda }}_{\mathrm{32}}^{\mathrm{2}}{)}_{n\times \mathrm{1}}\end{array}\right]\\ & -{\left[\begin{array}{c}({\mathit{\lambda }}_{\mathrm{35}}{e}^{{\mathit{\lambda }}_{\mathrm{35}}t}{)}_{n\times \mathrm{1}}\\ ({\mathit{\lambda }}_{\mathrm{38}}{e}^{{\mathit{\lambda }}_{\mathrm{38}}t}{)}_{n\times \mathrm{1}}\\ ({\mathit{\lambda }}_{\mathrm{32}}{e}^{{\mathit{\lambda }}_{\mathrm{32}}t}{)}_{n\times \mathrm{1}}\end{array}\right]}^{\text{T}}{\mathbf{\Sigma }}_{\mathrm{\Delta }}^{-\mathrm{1}}\left[\begin{array}{c}({\mathit{\lambda }}_{\mathrm{35}}{e}^{{\mathit{\lambda }}_{\mathrm{35}}t}{)}_{n\times \mathrm{1}}\\ ({\mathit{\lambda }}_{\mathrm{38}}{e}^{{\mathit{\lambda }}_{\mathrm{38}}t}{)}_{n\times \mathrm{1}}\\ ({\mathit{\lambda }}_{\mathrm{32}}{e}^{{\mathit{\lambda }}_{\mathrm{32}}t}{)}_{n\times \mathrm{1}}\end{array}\right]\end{array}\end{array}$$

$$\begin{array}{}\text{(C6)}& {\displaystyle }& {\displaystyle \frac{{\partial }^{\mathrm{2}}\mathcal{L}}{\partial t\partial \mathit{\alpha }}}={\displaystyle \frac{{\partial }^{\mathrm{2}}\mathcal{L}}{\partial \mathit{\alpha }\partial t}}=-{\left[\begin{array}{c}{\mathrm{0}}_{\mathrm{1}\times n}\\ \mathbf{W}\mathit{\gamma }\\ {\mathrm{0}}_{\mathrm{1}\times n}\end{array}\right]}^{\text{T}}{\mathbf{\Sigma }}_{\mathrm{\Delta }}^{-\mathrm{1}}\left[\begin{array}{c}({\mathit{\lambda }}_{\mathrm{35}}{e}^{{\mathit{\lambda }}_{\mathrm{35}}t}{)}_{n\times \mathrm{1}}\\ ({\mathit{\lambda }}_{\mathrm{38}}{e}^{{\mathit{\lambda }}_{\mathrm{38}}t}{)}_{n\times \mathrm{1}}\\ ({\mathit{\lambda }}_{\mathrm{32}}{e}^{{\mathit{\lambda }}_{\mathrm{32}}t}{)}_{n\times \mathrm{1}}\end{array}\right]\text{(C7)}& {\displaystyle }& {\displaystyle \frac{{\partial }^{\mathrm{2}}\mathcal{L}}{\partial t\partial \mathit{\beta }}}={\displaystyle \frac{{\partial }^{\mathrm{2}}\mathcal{L}}{\partial \mathit{\beta }\partial t}}=-{\left[\begin{array}{c}U\mathbf{W}\mathit{\gamma }\\ {\mathrm{0}}_{n\times \mathrm{1}}\\ {\mathrm{0}}_{n\times \mathrm{1}}\end{array}\right]}^{\text{T}}{\mathbf{\Sigma }}_{\mathrm{\Delta }}^{-\mathrm{1}}\left[\begin{array}{c}({\mathit{\lambda }}_{\mathrm{35}}{e}^{{\mathit{\lambda }}_{\mathrm{35}}t}{)}_{n\times \mathrm{1}}\\ ({\mathit{\lambda }}_{\mathrm{38}}{e}^{{\mathit{\lambda }}_{\mathrm{38}}t}{)}_{n\times \mathrm{1}}\\ ({\mathit{\lambda }}_{\mathrm{32}}{e}^{{\mathit{\lambda }}_{\mathrm{32}}t}{)}_{n\times \mathrm{1}}\end{array}\right]\text{(C8)}& {\displaystyle }& {\displaystyle \frac{{\partial }^{\mathrm{2}}\mathcal{L}}{\partial {\mathit{\alpha }}^{\mathrm{2}}}}=-{\left[\begin{array}{c}{\mathrm{0}}_{n\times \mathrm{1}}\\ \mathbf{W}\mathit{\gamma }\\ {\mathrm{0}}_{n\times \mathrm{1}}\end{array}\right]}^{\text{T}}{\mathbf{\Sigma }}_{\mathrm{\Delta }}^{-\mathrm{1}}\left[\begin{array}{c}{\mathrm{0}}_{n\times \mathrm{1}}\\ \mathbf{W}\mathit{\gamma }\\ {\mathrm{0}}_{n\times \mathrm{1}}\end{array}\right]\text{(C9)}& {\displaystyle }& {\displaystyle \frac{{\partial }^{\mathrm{2}}\mathcal{L}}{\partial {\mathit{\beta }}^{\mathrm{2}}}}=-{\left[\begin{array}{c}U\mathbf{W}\mathit{\gamma }\\ {\mathrm{0}}_{n\times \mathrm{1}}\\ {\mathrm{0}}_{n\times \mathrm{1}}\end{array}\right]}^{\text{T}}{\mathbf{\Sigma }}_{\mathrm{\Delta }}^{-\mathrm{1}}\left[\begin{array}{c}U\mathbf{W}\mathit{\gamma }\\ {\mathrm{0}}_{n\times \mathrm{1}}\\ {\mathrm{0}}_{n\times \mathrm{1}}\end{array}\right]\text{(C10)}& {\displaystyle }& {\displaystyle \frac{{\partial }^{\mathrm{2}}\mathcal{L}}{\partial \mathit{\alpha }\partial \mathit{\beta }}}={\displaystyle \frac{{\partial }^{\mathrm{2}}\mathcal{L}}{\partial \mathit{\beta }\partial \mathit{\alpha }}}=-{\left[\begin{array}{c}U\mathbf{W}\mathit{\gamma }\\ {\mathrm{0}}_{n\times \mathrm{1}}\\ {\mathrm{0}}_{n\times \mathrm{1}}\end{array}\right]}^{\text{T}}{\mathbf{\Sigma }}_{\mathrm{\Delta }}^{-\mathrm{1}}\left[\begin{array}{c}{\mathrm{0}}_{n\times \mathrm{1}}\\ \mathbf{W}\mathit{\gamma }\\ {\mathrm{0}}_{n\times \mathrm{1}}\end{array}\right],\end{array}$$

Appendix D

Additional derivatives are required to propagate the uncertainty of the overdispersion parameters ω. This can only be done manually if the overdispersion is attributed to the concordia intercept age t, using the simplified model (ignoring the uncertainty of W). In that case,

$$\begin{array}{}\text{(D1)}& {\displaystyle }& {\displaystyle \frac{{\partial }^{\mathrm{2}}\mathcal{L}}{\partial \mathit{\gamma }\partial \mathit{\omega }}}={\left({\displaystyle \frac{{\partial }^{\mathrm{2}}\mathcal{L}}{\partial \mathit{\omega }\partial \mathit{\gamma }}}\right)}^{\text{T}}=-{\mathbf{\Delta }}^{\text{T}}{\displaystyle \frac{\partial {\mathbf{\Sigma }}_{\mathrm{\Delta }}^{-\mathrm{1}}}{\partial \mathit{\omega }}}\left[\begin{array}{c}U\mathit{\beta }\mathbf{W}\\ \mathit{\alpha }\mathbf{W}\\ I_{n\times n}\end{array}\right]\text{(D2)}& {\displaystyle }& {\displaystyle \frac{{\partial }^{\mathrm{2}}\mathcal{L}}{\partial t\partial \mathit{\omega }}}={\left({\displaystyle \frac{{\partial }^{\mathrm{2}}\mathcal{L}}{\partial \mathit{\omega }\partial t}}\right)}^{\text{T}}=-{\mathbf{\Delta }}^{\text{T}}{\displaystyle \frac{\partial {\mathbf{\Sigma }}_{\mathrm{\Delta }}^{-\mathrm{1}}}{\partial \mathit{\omega }}}\left[\begin{array}{c}({\mathit{\lambda }}_{\mathrm{35}}{e}^{{\mathit{\lambda }}_{\mathrm{35}}t}{)}_{n\times \mathrm{1}}\\ ({\mathit{\lambda }}_{\mathrm{38}}{e}^{{\mathit{\lambda }}_{\mathrm{38}}t}{)}_{n\times \mathrm{1}}\\ ({\mathit{\lambda }}_{\mathrm{32}}{e}^{{\mathit{\lambda }}_{\mathrm{32}}t}{)}_{n\times \mathrm{1}}\end{array}\right]\text{(D3)}& {\displaystyle }& {\displaystyle \frac{{\partial }^{\mathrm{2}}\mathcal{L}}{\partial \mathit{\alpha }\partial \mathit{\omega }}}={\left({\displaystyle \frac{{\partial }^{\mathrm{2}}\mathcal{L}}{\partial \mathit{\omega }\partial \mathit{\alpha }}}\right)}^{\text{T}}=-{\mathbf{\Delta }}^{\text{T}}{\displaystyle \frac{\partial {\mathbf{\Sigma }}_{\mathrm{\Delta }}^{-\mathrm{1}}}{\partial \mathit{\omega }}}\left[\begin{array}{c}{\mathrm{0}}_{n\times \mathrm{1}}\\ \mathbf{W}\mathit{\gamma }\\ {\mathrm{0}}_{n\times \mathrm{1}}\end{array}\right]\text{(D4)}& {\displaystyle }& {\displaystyle \frac{{\partial }^{\mathrm{2}}\mathcal{L}}{\partial \mathit{\beta }\partial \mathit{\omega }}}={\left({\displaystyle \frac{{\partial }^{\mathrm{2}}\mathcal{L}}{\partial \mathit{\omega }\partial \mathit{\beta }}}\right)}^{\text{T}}=-{\mathbf{\Delta }}^{\text{T}}{\displaystyle \frac{\partial {\mathbf{\Sigma }}_{\mathrm{\Delta }}^{-\mathrm{1}}}{\partial \mathit{\omega }}}\left[\begin{array}{c}UW\mathit{\gamma }\\ {\mathrm{0}}_{n\times \mathrm{1}}\\ {\mathrm{0}}_{n\times \mathrm{1}}\end{array}\right]\text{(D5)}& {\displaystyle }& {\displaystyle \frac{{\partial }^{\mathrm{2}}\mathcal{L}}{\partial {\mathit{\omega }}^{\mathrm{2}}}}=-{\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}\left({\displaystyle \frac{{\partial }^{\mathrm{2}}\ln \left|{\mathbf{\Sigma }}_{\mathrm{\Delta }}\right|}{\partial {\mathit{\omega }}^{\mathrm{2}}}}+{\mathbf{\Delta }}^{\text{T}}{\displaystyle \frac{{\partial }^{\mathrm{2}}{\mathbf{\Sigma }}_{\mathrm{\Delta }}^{-\mathrm{1}}}{\partial {\mathit{\omega }}^{\mathrm{2}}}}\mathbf{\Delta }\right),\end{array}$$

with

$$\begin{array}{}\text{(D6)}& {\displaystyle \frac{\partial {\mathbf{\Sigma }}_{\mathrm{\Delta }}^{-\mathrm{1}}}{\partial \mathit{\omega }}}=-{\mathbf{\Sigma }}_{\mathrm{\Delta }}^{-\mathrm{1}}{\displaystyle \frac{\partial {\mathbf{\Sigma }}_{\mathrm{\Delta }}}{\partial \mathit{\omega }}}{\mathbf{\Sigma }}_{\mathrm{\Delta }}^{-\mathrm{1}}\end{array}$$

$$\begin{array}{}\text{(D7)}& {\displaystyle }\begin{array}{rl}& {\displaystyle \frac{{\partial }^{\mathrm{2}}{\mathbf{\Sigma }}_{\mathrm{\Delta }}^{-\mathrm{1}}}{\partial {\mathit{\omega }}^{\mathrm{2}}}}=\\ & -\left({\displaystyle \frac{\partial {\mathbf{\Sigma }}_{\mathrm{\Delta }}^{-\mathrm{1}}}{\partial \mathit{\omega }}}{\displaystyle \frac{\partial {\mathbf{\Sigma }}_{\mathrm{\Delta }}}{\partial \mathit{\omega }}}{\mathbf{\Sigma }}_{\mathrm{\Delta }}^{-\mathrm{1}}+{\mathbf{\Sigma }}_{\mathrm{\Delta }}^{-\mathrm{1}}{\displaystyle \frac{{\partial }^{\mathrm{2}}{\mathbf{\Sigma }}_{\mathrm{\Delta }}}{\partial {\mathit{\omega }}^{\mathrm{2}}}}{\mathbf{\Sigma }}_{\mathrm{\Delta }}^{-\mathrm{1}}+{\mathbf{\Sigma }}_{\mathrm{\Delta }}^{-\mathrm{1}}{\displaystyle \frac{\partial {\mathbf{\Sigma }}_{\mathrm{\Delta }}}{\partial \mathit{\omega }}}{\displaystyle \frac{\partial {\mathbf{\Sigma }}_{\mathrm{\Delta }}^{-\mathrm{1}}}{\partial \mathit{\omega }}}\right)\end{array}\text{(D8)}& {\displaystyle \frac{{\partial }^{\mathrm{2}}\ln \left|{\mathbf{\Sigma }}_{\mathrm{\Delta }}\right|}{\partial {\mathit{\omega }}^{\mathrm{2}}}}=\mathrm{Tr}\left({\displaystyle \frac{\partial {\mathrm{\Sigma }}_{\mathrm{\Delta }}^{-\mathrm{1}}}{\partial \mathit{\omega }}}{\displaystyle \frac{\partial {\mathbf{\Sigma }}_{\mathrm{\Delta }}}{\partial \mathit{\omega }}}+{\mathrm{\Sigma }}_{\mathrm{\Delta }}^{-\mathrm{1}}{\displaystyle \frac{{\partial }^{\mathrm{2}}{\mathbf{\Sigma }}_{\mathrm{\Delta }}}{\partial {\mathit{\omega }}^{\mathrm{2}}}}\right),\end{array}$$

in which Tr(∗) stands for the trace of ∗ and

$$\begin{array}{}\text{(D9)}& {\displaystyle \frac{\partial {\mathbf{\Sigma }}_{\mathrm{\Delta }}}{\partial \mathit{\omega }}}& {\displaystyle }=\mathrm{2}{\mathbf{J}}_{\mathit{\omega }}^{\text{T}}\mathit{\omega }{\mathbf{J}}_{\mathit{\omega }}\text{(D10)}& {\displaystyle \frac{{\partial }^{\mathrm{2}}{\mathbf{\Sigma }}_{\mathrm{\Delta }}}{\partial {\mathit{\omega }}^{\mathrm{2}}}}& {\displaystyle }=\mathrm{2}{\mathbf{J}}_{\mathit{\omega }}^{\text{T}}{\mathbf{J}}_{\mathit{\omega }}.\end{array}$$

Explicit formulae for the second derivatives are not available for the common-Pb-based overdispersion model. In that case, the Fisher information matrix must be computed numerically.