Production of ⁴⁰Ar by an overlooked mode of ⁴⁰K decay with implications for K-Ar geochronology

The decay of ⁴⁰K to the stable isotopes ⁴⁰Ca and ⁴⁰Ar is used as a measure of time for both the K-Ca and K-Ar geochronometers, the latter of which is most generally utilized by the variant ⁴⁰Ar∕³⁹Ar system. The increasing precision of geochronology has forced practitioners to deal with the systematic uncertainties rooted in all radioisotope dating methods. A major component of these systematic uncertainties for the K-Ar and ⁴⁰Ar∕³⁹Ar techniques is imprecisely determined decay constants and an incomplete knowledge of the decay scheme of ⁴⁰K. Recent geochronology studies question whether ⁴⁰K can decay to ⁴⁰Ar via an electron capture directly to ground state (EC_ground), citing the lack of experimental verification as reasoning for its omission. In this study, we (1) provide a theoretical argument in favor of the presence of this decay mode and (2) evaluate the magnitude of this decay mode by calculating the electron capture to positron ratio (${\mathrm{EC}}_{\mathrm{ground}}/{\mathit{\beta }}^{+}$) and comparing calculated ratios to previously published calculations, which yield ${\text{EC}}_{\mathrm{ground}}/{\mathit{\beta }}^{+}$ between 150–212. We provide support for this calculation through comparison of the experimentally verified EC${}_{\mathrm{ground}}/{\mathit{\beta }}^{+}$ ratio of ²²Na with our calculation using the theory of β decay. When combined with measured values of β⁺ and β⁻ decay rates, the best estimate for the calculated EC${}_{\mathrm{ground}}/{\mathit{\beta }}^{+}$ for ⁴⁰K yields a partial decay constant for ⁴⁰K direct to ground-state ⁴⁰Ar of $\mathrm{11.6}\pm \mathrm{1.5}\times {\mathrm{10}}^{-\mathrm{13}}$ a⁻¹ (2σ). We calculate a partial decay constant of ⁴⁰K to ⁴⁰Ar of $\mathrm{0.592}\pm \mathrm{0.014}\times {\mathrm{10}}^{-\mathrm{10}}$ a⁻¹ and a total decay constant of $\mathrm{5.475}\pm \mathrm{0.107}\times {\mathrm{10}}^{-\mathrm{10}}$ a⁻¹ (2σ), and we conclude that although omission of this decay mode can be significant for K-Ar dating, it is minor for ⁴⁰Ar∕³⁹Ar geochronology and is therefore unlikely to have significantly biased published measurements.

1 Introduction

⁴⁰K is a naturally occurring radioisotope of K with atomic abundance of 0.0117 % (Garner et al., 1975). ⁴⁰K undergoes a branched decay to ⁴⁰Ar and ⁴⁰Ca with a total half-life of ca. 1.3 Ga and is the basis of the K-Ca and the K-Ar geochronometers (Aldrich and Nier, 1948; Wasserburg and Hayden, 1955; Marshall and DePaolo, 1982). The K-Ar system is most often exploited using the variant ⁴⁰Ar∕³⁹Ar method, wherein some of the ³⁹K in the sample is transmuted to ³⁹Ar by irradiation with fast neutrons, thereby allowing both the parent and the daughter nuclides to be measured as isotopes of Ar (Merrihue and Turner, 1966). The latter is widely used to date geological events that span Earth's history, from volcanic eruptions recorded in historical texts (e.g., Preece et al., 2018; Renne et al., 1997) to the earliest events in the solar system (e.g., Renne, 2000).

Advances in analytical precision have forced practitioners in geochronology to address systematic uncertainties that are inherent in all radioisotope dating methods, such as uncertainties in the measurement apparatus, prior assumptions made by the observer, or interference from environmental factors. For the K-Ar system, these uncertainties also include those that arise from imprecisely known decay rates of ⁴⁰K. In the geological literature, there have been two influential reviews of measurements of the ⁴⁰K decay rate. Beckinsale and Gale (1969) provided the first comprehensive review of measured and predicted decay rates, which became the basis of the convention adopted by Steiger and Jäger (1977) used by the geochronological community for the next 20 years. Subsequently, Min et al. (2000) provided a more lengthy, critical review of available specific activity data determined by direct measurements of decay and updated the derived decay rates for newer physical constants. More recently, the ⁴⁰K decay parameters were estimated by Renne et al. (2010, 2011), and although direct measurements of the ⁴⁰K decay were incorporated into the estimate, it was heavily weighted to an intercomparison with ²³⁸U decay. The decay rate determined by Renne et al. (2010, 2011), and the Min et al. (2000) decay rates are the most frequently used in ⁴⁰Ar∕³⁹Ar geochronology. These evaluations, along with those from the nuclear physics community, have been summarized recently by Cresswell et al. (2018, 2019).

Despite decades of work and long-standing interest in ⁴⁰K decay, there remains uncertainty over the nature of the decay scheme. There is consensus that most ⁴⁰K decays by β⁻ to ⁴⁰Ca or by electron capture to ⁴⁰Ar via an excited state and that a small amount (∼0.001 %) of ⁴⁰K decays to ⁴⁰Ar via β⁺. The early but influential review of ⁴⁰K decay by Beckinsale and Gale (1969) included these decay modes and also included a prediction of a second electron capture decay directly to the ground state of ⁴⁰Ar that would add an additional ∼2 % to the rate of decay from ⁴⁰K to ⁴⁰Ar. Many workers in geochronology (e.g., those who use the Min et al., 2000, decay constants) have ignored this prediction, and some nuclear physics tabulations do not clearly include it (Endt, 1990; Audi et al., 2003). The influential review by Min et al. (2000) described this decay mode as “unverified” and having a “questionable” existence.

However, the putative electron capture to ground-state decay-mode decay constant is of the same order of magnitude as the uncertainties in the decay rate of ⁴⁰K to ⁴⁰Ar and therefore may be a non-negligible and potentially important part of the geochronological system. Here, we describe the theoretical basis of this predicted decay mode and demonstrate the robust nature of the prediction via an analogous calculation of ²²Na decay. We describe experiments that could be made to measure this decay mode and also identify observations from nuclear physics experiments that offer evidence for its existence. We conclude that the evidence for this decay mode is strong and, despite the large uncertainty, should be considered in evaluations of the ⁴⁰K decay rate.

2 Historical overview

At present, ⁴⁰K has three experimentally verified decay modes (Fig. 1).

1. β⁻ decay to ⁴⁰Ca, this mode can be verified by direct measurement of the β⁻ emission.

2. Electron capture to an excited isomer of ⁴⁰Ar, followed by decay to the ground state of ⁴⁰Ar accompanied by emission of a 1.46 MeV γ-ray. Hereafter, we denote this decay mode as EC*. This mode can be verified by direct measurement of the γ emission.

3. β⁺ decay from the ground state of ⁴⁰K to the ground state of ⁴⁰Ar (Engelkemeir et al., 1962), this is a very small component of the total decay rate and has been verified by direct measurement of the β⁺ emission.

In their paper reporting the measurement of ${\mathit{\beta }}^{+}/{\mathit{\beta }}^{-}$, Engelkemeir et al. (1962), through private correspondence with Brosi and Kettle, proposed that an electron capture mode that goes directly to ground-state ⁴⁰Ar also exists, with an electron capture to positron ratio of 155. This decay mode is hereafter denoted EC_ground. This decay mode has not been experimentally detected, in part because the measurement is much more difficult to make than the others. If it exists, it would contribute about 0.2 % to the total decay rate of ⁴⁰K or about 2 % to the ⁴⁰Ar branch.

The EC_ground decay mode was included in the review by Beckinsale and Gale (1969) and then subsequently in Steiger and Jäger (1977). This decay mode is also included in the widely used Evaluated Nuclear Structure Data File (ENSDF) and Decay Data Evaluation Project (DDEP) evaluations (Chen, 2017; Mougeot and Helmer, 2009, respectively). However, evaluations by Endt and Van der Leun (1973, 1978), Endt (1990), and Audi et al. (2003) do not explicitly include this decay mode, with Audi et al. (2003) giving a transition intensity that is the combined EC* and β⁺ intensities. Min et al. (2000) have questioned its validity because there is no experimental verification and therefore do not include EC_ground in their estimates.

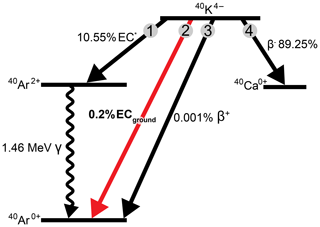
Figure 1 Decay scheme of ⁴⁰K following McDougall and Harrison (1999) and Leutz et al. (1965), where 1 is the electron capture branch to the excited state of ⁴⁰Ar with y-ray emission (EC*), 2 is the electron capture direct to the ground state of ⁴⁰Ar (EC_ground), 3 is the positron decay to ground state of ⁴⁰Ar, and 4 is the β decay to the ground state of ⁴⁰Ca. The disputed decay mode, EC_ground, is highlighted in red.

3 Why there must be an EC_ground decay mode

In nuclides that are too proton-rich and therefore radioactive, protons decay to correct this imbalance via two mechanisms. Either, (1) the nucleus undergoes electron capture wherein an orbital electron is captured by the nucleus, or (2) the nucleus emits a positron (β⁺). Both processes are types of β decay and result in the transformation of a proton to a neutron to conserve charge, and they both also emit a neutrino in order to conserve lepton number and energy. These two processes are typically paired: coupled electron capture–β⁺ is the second most abundant decay type on the chart of the nuclides, after β⁻ decay (Audi et al., 2003). The electron capture (EC) and positron (β⁺) decay modes are linked because both processes have the same initial and final nuclear states.

β⁺ decay is always accompanied by EC, but the converse is not always true (Bambynek et al., 1977). This is because β⁺ decay, unlike EC, requires a minimum amount of energy (∼1022 keV, equivalent to the combined rest masses of both a positron and an electron) in order to produce the emitted positron and an electron (the latter to satisfy charge conservation). The energy between initial and final states is the Q value, which is a function of the difference between the initial and final masses. This energy is shared between the outgoing neutrino, atomic excitation of the daughter system, recoil energy, and nuclear excitation of the daughter system. The energy that dictates if positron emission is possible is denoted Q_EC. In the decay of ⁴⁰K, the EC* branch has an energy difference (Q_EC) between the initial and excited isomer state of only 44 keV. In contrast, the energy difference between ⁴⁰K and the ground state of ⁴⁰Ar is 1504.4 keV (Wang et al., 2017), an energy greater than the combined rest masses of the positron and electron. Therefore, the EC* branch, with an energy difference of only 44 keV, cannot be the complement to the β⁺ decay, and the EC_ground must exist to provide the β⁺ complement. The experimental observation of the β⁺ decay mode comes from a single measurement by Engelkemeir et al. (1962). We rely on this measurement to make our argument for the existence the EC_ground. It is possible that the positrons observed arise from the pair production of the ∼1460 keV gamma; Engelkemier et al. (1962) discuss this possibility in their experiment, calculating this as 55 %–60 % of the total positron detection rate. However, positrons produced by this mode of pair production would be monoenergetic at 440 keV, whereas the observed positron energy spectra exceed this value, with a maximum of 491 keV. A reasonable fit is also observed between the measured β⁺ energy spectrum and the theoretical third forbidden unique energy spectrum, supporting the argument that these β⁺ are from a decay mode rather than arising from pair production.

4 Theory and calculation of EC${}_{\mathrm{ground}}/{\mathit{\beta }}^{+}$

In the decay of ⁴⁰K, the nuclide can reach a more stable state (⁴⁰Ca or ⁴⁰Ar) only by violating quantum selection rules. Quantum selection rules place formal constraints of the possible transitions of a system from one quantum state to another. In this case it places constraints on the possible set of transitions from the parent ⁴⁰K state to the daughter ⁴⁰Ar. Decays which violate these selection rules undergo slow, so-called “forbidden” unique transitions, which give ⁴⁰K its long ∼1.3 Ga half-life. The ⁴⁰K decay scheme itself is unusual because the coupled EC_ground-β⁺ and β⁻ branches are the only third-order unique forbidden transitions known in nature. All ⁴⁰K decays undergo a parity reversal (where parity reversal is the change of sign in one of the spatial coordinates $(x,y,z)$) between the initial parent state and final daughter state. Therefore, we can define the selection rules as follows:

$$(\mathrm{|}\mathrm{\Delta }J-\mathrm{1}\mathrm{|})\text{st order unique forbidden decay},$$

where $\mathrm{\Delta }J=J_i-J_f$, is the change in spin from initial to final state following Krane and Halliday (1987). We can characterize each decay mode of ⁴⁰K by its degree of forbiddenness from the above selection rule. The EC* mode undergoes a spin change of $\mathrm{\Delta }J=\mathrm{4}-\mathrm{2}=\mathrm{2}$ and is classified as a first-order unique forbidden decay. The three other decay modes of ⁴⁰K, including EC_ground, all undergo a spin change of $\mathrm{\Delta }J=\mathrm{4}-\mathrm{0}=\mathrm{4}$ and are classified as third-order unique forbidden decays.

The EC process occurs because the atomic electrons have a finite probability to be in the nucleus with the likelihood of being captured highest for those closest to the nucleus. A theoretical description of β emission was first given by Fermi (1934), while the possibility of electron capture was first recognized by Yukawa and Sakata (1935) and later developed by Bethe and Bacher (1936). Here we use Fermi theory of β⁻ decay to calculate the EC${}_{\mathrm{ground}}/{\mathit{\beta }}^{+}$ in the decay of ⁴⁰K.

We can use the ratio of orbital electron capture and positron emission to infer the existence of EC_ground. The ratio br is defined as follows:

$$\begin{array}{}\text{(1)}& \text{br}={\displaystyle \frac{{\mathit{\lambda }}_{\mathrm{ec}}}{{\mathit{\lambda }}_{{\mathit{\beta }}^{+}}}},\end{array}$$

where λ_ec and λ_β+ are the probability per unit time of electron capture or β⁺ emission. In electron capture, orbital electrons can be captured from any orbital shell of the atom. The $\text{EC}/{\mathit{\beta }}^{+}$ is therefore the summation of the individual capture ratios from each shell. Following Bambynek et al. (1977), the total electron capture-to-positron ratio is as follows:

$$\begin{array}{}\text{(2)}& {\displaystyle \frac{{\mathit{\lambda }}_x}{{\mathit{\lambda }}_{{\mathit{\beta }}^{+}}}}={\displaystyle \frac{\sum _x{n}_x{C}_x{f}_x}{f_{{\mathit{\beta }}^{+}}C\left(W\right)}},\end{array}$$

where x is the shell, n_x is the relative occupation number, C_x contains the dependence of electron capture rates on nuclear structure giving the forbiddenness classification, similar to the shape factor in β decay (Emery, 1975), f_x is the integrated fermi function in β decay, $f_{{\mathit{\beta }}^{+}}$ is the integrated positron spectrum, and C(W) is the theoretical shape factor for allowed or forbidden transitions. A review of shape factors for ⁴⁰K transitions is provided by Cresswell et al. (2018, 2019). We initially simplify this equation to only consider the innermost K shell, the shell containing the electron with the highest probability to be captured by the nucleus:

$$\begin{array}{}\text{(3)}& {\displaystyle \frac{{\mathit{\lambda }}_{\mathrm{K}}}{{\mathit{\lambda }}_{{\mathit{\beta }}^{+}}}}={\displaystyle \frac{n_{\mathrm{K}}{C}_{\mathrm{K}}{f}_{\mathrm{K}}}{f_{{\mathit{\beta }}^{+}}C\left(W\right)}},\end{array}$$

where λ_K is the probability of K shell capture. For this capture, f_K is defined as follows:

$$\begin{array}{}\text{(4)}& f_{\mathrm{K}}={\displaystyle \frac{\mathit{\pi }}{\mathrm{2}}}{q}_{\mathrm{K}}^{\mathrm{2}}{\mathit{\beta }}_{\mathrm{K}}^{\mathrm{2}}{B}^{\mathrm{K}},\end{array}$$

where q_K is the momentum of the neutrino particle, β_K is the Coulomb amplitude of the wave function, and B_K is the term for overlap and exchange corrections. Similarly, f_β+ is defined as follows:

$$\begin{array}{}\text{(5)}& {\displaystyle }{f}_{{\mathit{\beta }}^{+}}=\underset{\mathrm{1}}{\overset{W_{\mathrm{0}}}{\int }}F\left(-Z,W\right)Wp(W_{\mathrm{0}}-W{)}^{\mathrm{2}}\mathrm{d}W,\text{(6)}& {\displaystyle }W=\mathrm{1}+{\displaystyle \frac{E_T}{m_{\mathrm{e}}}},\text{(7)}& {\displaystyle }{W}_{\mathrm{0}}=\mathrm{1}+{\displaystyle \frac{E_{\max }}{m_{\mathrm{e}}}},\text{(8)}& {\displaystyle }p=\sqrt{W^{\mathrm{2}}-\mathrm{1}},\end{array}$$

where W is the total energy of the positron given by its kinetic energy E_T and rest mass m_e, defined above, and the momentum of the positron is given by p (Eq. 8); W₀ is the total normalized energy defined above; E_max is the upper limit of the positron energy (equal to the Q value of the decay); and $F(-Z,W)$ is the Fermi function. We follow Bambynek et al. (1977) in the formula for $\frac{C_{\mathrm{K}}}{\mathrm{C}\left(\mathrm{W}\right)}$ which is given by

$$\begin{array}{}\text{(9)}& \begin{array}{rl}{\displaystyle \frac{C_{\mathrm{K}}}{\overline{C\left(W\right)}}}& =[\left(\mathrm{2}L-\mathrm{1}\right)\mathrm{!}{]}^{-\mathrm{1}}{q}_{\mathrm{K}}^{\mathrm{2}(L-\mathrm{1})}\left\{\sum _{n=\mathrm{1}}^L{\mathit{\lambda }}_n{p}^{\mathrm{2}\left(n-\mathrm{1}\right)}\left(\left(\mathrm{2}n-\mathrm{1}\right)\mathrm{!}\right.\right.\\ & {\left.{\left.\cdot \left[\mathrm{2}\left(L-n\right)+\mathrm{1}\right]\mathrm{!}\right)}^{-\mathrm{1}}\right\}}^{-\mathrm{1}}\end{array},\end{array}$$

where L=ΔJ and L=1 for ΔJ=0. The parameter λ_n cannot be calculated in a straightforward manner and therefore we follow a typical assumption that λ_n=1 (Huber, 2011). This reduces the above expression to

$$\begin{array}{}\text{(10)}& {\displaystyle \frac{C_{\mathrm{K}}}{\overline{C\left(W\right)}}}={\displaystyle \frac{q_{\mathrm{K}}^{\mathrm{6}}}{p^{\mathrm{6}}+q^{\mathrm{6}}+\mathrm{7}{p}^{\mathrm{2}}{q}^{\mathrm{2}}(p^{\mathrm{2}}+q^{\mathrm{2}})}}.\end{array}$$

In a given decay, the change in charge from the initial to final state can lead to an imperfect overlap of the wave functions of these states. Furthermore, given the indistinguishability of electrons, there is the possibility of an exchange effect wherein an electron does not necessarily come from the orbital where the vacancy appears. For instance, it is possible that a vacancy may appear in the K-shell, but the captured electron from an outer shell is then subsequently filled by the inner shell electron (Bahcall, 1962; Bambynek et al., 1977). We follow Bahcall (1962) in implementing corrections for these effects, resulting in B_K=0.979. Following this, using nuclear data given in Bambynek et al. (1977), we estimate an EC${}_{\mathrm{ground}}/{\mathit{\beta }}^{+}$ of 148.

We first note that this value is in approximate concordance with the private correspondence value in Engelkemeir et al. (1962). However, this is only the capture ratio from the K shell, so we extend our model to a total electron capture ratio from all orbitals following Bosch et al. (1977). The total electron capture to positron ratio, an extension of Eq. (1), is given by

$$\begin{array}{}\text{(11)}& {\displaystyle \frac{\text{EC}}{{\mathit{\beta }}^{+}}}={\displaystyle \frac{K}{{\mathit{\beta }}^{+}}}\left(\mathrm{1}+{\displaystyle \frac{L}{K}}+{\displaystyle \frac{M}{L}}{\displaystyle \frac{L}{K}}+\mathrm{\dots }\right).\end{array}$$

We can simplify this equation by neglecting shells that make a negligible contribution. In ⁴⁰K the probability of capture is dominated by the two inner shells K and L1, with approximate probability of ca. ∼90 % and ∼10 % and a negligible contribution from the shells further out. We can therefore omit all shell captures except K and L1 to arrive at the total EC${}_{\mathrm{ground}}/{\mathit{\beta }}^{+}$ ratio:

$$\begin{array}{}\text{(12)}& {\displaystyle \frac{\text{EC}}{{\mathit{\beta }}^{+}}}={\displaystyle \frac{K}{{\mathit{\beta }}^{+}}}\left(\mathrm{1}+{\displaystyle \frac{L_{\mathrm{1}}}{K}}\right).\end{array}$$

The ratio of each shell capture can be solved with the following equation:

$$\begin{array}{}\text{(13)}& {\displaystyle \frac{x}{K}}={\displaystyle \frac{{\mathit{\beta }}_x^{\mathrm{2}}(W_{\mathrm{0}}-W_x{)}^{\mathrm{2}}{B}_x}{{\mathit{\beta }}_{\mathrm{K}}^{\mathrm{2}}(W_{\mathrm{0}}-W_x{)}^{\mathrm{2}}{B}_{\mathrm{K}}}},\end{array}$$

where x=L1 and the other symbols have the same definition as above. Using this equation we calculate a total EC${}_{\mathrm{ground}}/{\mathit{\beta }}^{+}$ of 164.

To further estimate the magnitude of the electron capture decay mode, we can perform another calculation of EC${}_{\mathrm{ground}}/{\mathit{\beta }}^{+}$ following Fireman (1949). This simplified form of the calculating EC${}_{\mathrm{ground}}/{\mathit{\beta }}^{+}$ is dependent only on the Q value (the difference between the initial and final state energies). This is given by

$$\begin{array}{}\text{(14)}& \begin{array}{rl}& {\displaystyle \frac{{\mathit{\lambda }}_{\mathrm{EC}}}{{\mathit{\lambda }}_{{\mathit{\beta }}^{+}}}}={\displaystyle \frac{(\mathit{\eta }+\mathrm{2}{)}^{\mathrm{8}}}{\mathrm{0.450}{\mathit{\eta }}^{\mathrm{6.5}}}}\\ & \cdot {\displaystyle \frac{\mathrm{1}}{\mathrm{0.0676}+\mathrm{1.25}\mathit{\eta }+\mathrm{8.48}{\mathit{\eta }}^{\mathrm{2}}+\mathrm{12.5}{\mathit{\eta }}^{\mathrm{3}}+\mathrm{1.74}{\mathit{\eta }}^{\mathrm{4}}+\mathrm{0.079}{\mathit{\eta }}^{\mathrm{6}}}}\end{array},\end{array}$$

where $\mathit{\eta }=\frac{Q}{m_{\mathrm{e}}}-\mathrm{2}$. We calculate an EC${}_{\mathrm{ground}}/{\mathit{\beta }}^{+}$ of 272 using this method and the updated Q value of Wang et al. (2017). We note that despite discrepancies in these values for each method of evaluation, they are of the same order of magnitude. The differences in the values in these evaluations highlight the need for experimental measurement of EC${}_{\mathrm{ground}}/{\mathit{\beta }}^{+}$.

5 Comparison with other evaluations

Other theoretical evaluations of EC${}_{\mathrm{ground}}/{\mathit{\beta }}^{+}$ for ⁴⁰K exist in the literature (Fig. 2). Pradler et al. (2013) and Mougeot (2018) report ratios of 150 and 212±0.15, respectively (uncertainties are reported where they have been estimated). These workers use broadly similar methods to us. Mougeot (2018) uses higher-order corrections for both exchange and overlap and accounts for the dependence of λ_K, that we set equal to 1 in Eq. (9) using the energy of the decay. Pradler et al. (2013) use the Fermi method and data from Bambynek et al. (1977) but only perform the calculation for K-shell electrons, resulting in a slightly differently calculated value than we report. Notably, all estimated values are of the same order of magnitude, similar to the ratio 155 reported in Engelkemeir et al. (1962) and our calculated value of 164. Currently, the most commonly used EC${}_{\mathrm{ground}}/{\mathit{\beta }}^{+}$ value is calculated via the LogFT program, a program used in nuclear data evaluations (ENSDF collaboration, LogFT). However, the program is capable of only calculating first and second unique forbidden decay ratios, so the EC${}_{\mathrm{ground}}/{\mathit{\beta }}^{+}$ value from LogFT of 200±100 is an extrapolation, with the assumption that the increase in the ratio from second to third order is by the same factor as the increase from first to second order. Finally, Chen (2017) evaluates the ⁴⁰K decay data and reports a EC${}_{\mathrm{ground}}/{\mathit{\beta }}^{+}$ value of 45.2±1.4 without elaboration.

The variability between the modern estimates are driven primarily by choices when making the approximations necessary for these calculations to be tractable. Uncertainties on individual estimates that could be derived by propagating the uncertainties in the underlying experimental data are small, and where uncertainties are estimated, they are generally not explicated.

The value calculated by Mougeot (2018) of 212±0.15 is currently the best estimate of the ⁴⁰K EC${}_{\mathrm{ground}}/{\mathit{\beta }}^{+}$. It is slightly higher than two other recent estimates, our value of 164 or that of Pradler et al. (2013) of 150. Given a broad consensus in calculated EC${}_{\mathrm{ground}}/{\mathit{\beta }}^{+}$ over several decades and via a variety of methods, it appears highly likely that it falls in the range 150–212 (Fig. 2).

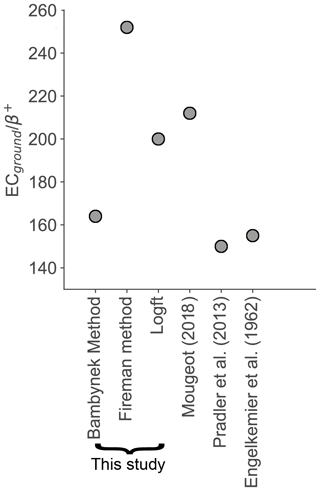
Figure 2 Comparison of theoretically calculated EC${}_{\mathrm{ground}}/{\mathit{\beta }}^{+}$ of ⁴⁰K in this study using three methods: (1) Bambynek method (Bambynek et al., 1977), (2) Fireman method (Fireman, 1949), and (3) LogFT (ENSDF collaboration, 2020, LogFT). The value of Chen (2017) is not included in the figure as it is an extreme outlier, and the authors do not explain the method they use to reach this value. Our calculated ratios are compared to previous evaluations in the literature (Engelkemeir et al., 1962; Pradler et al., 2013; Mougeot, 2018). Uncertainties in these values are either intractable or, in the case of Mougeot (2018), too small to plot. Note the consistency in the estimated ratio from all of the methods. Uncertainties are unknown in all cases except Mougeot (2018), where the uncertainty is too small to plot.

6 Comparison with ²²Na

To test the validity of our ⁴⁰K EC${}_{\mathrm{ground}}/{\mathit{\beta }}^{+}$ estimate, we use the same calculations to estimate the experimentally constrained ($\text{EC}/{\mathit{\beta }}^{+})$* value for ²²Na decay. ²²Na is radionuclide with a half-life of ∼2.6 years, it occurs in nature as a low-abundance cosmogenic nuclide produced by spallation of ⁴⁰Ar and is also produced synthetically by proton irradiation for use in positron emission tomography. Like ⁴⁰K, it decays by electron capture and positron emission. The main EC–β⁺ pair for ²²Na decays initially to the excited state of ²²Ne, followed by a 1.27 MeV γ emission (Fig. 3; Bé et al., 2010). This pair has a ($\text{EC}/{\mathit{\beta }}^{+})$* of approximately 0.1 and accounts for >99.9 % of the total decay. A second EC–β⁺ pair decays directly to the ground state of ²²Na with an ($\text{EC}/{\mathit{\beta }}^{+}{)}_{\mathrm{ground}}$ of ∼0.02, but it is a minor component. Here, we calculate the ($\text{EC}/{\mathit{\beta }}^{+})$* for the main branch. Unlike ⁴⁰K, the dominant decay of ²²Na is the β⁺ decay mode. This is due to the greater difference in energy between the initial and final states, as positron decay will have a greater possibility of occurring in decays with a greater mass differences between initial and final states (Emery, 1975). ²²Na is not a perfect analogue; however, it is probably the best choice that has both a tractable theoretical calculation and a wealth of experimental data that can be used readily for verification.

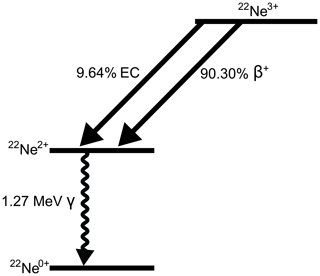
Figure 3 Decay scheme of ²²Na following Bé et al. (2010) and Leutz et al. (1965). An additional EC and β⁺ decay pair that corresponds to approximately 0.056 % of the total decay of ²²Na has been omitted for clarity.

Unlike ⁴⁰K, there are numerous measurements of the electron capture to positron ratio for decay to the excited state of ²²Ne (Fig. 4; Kreger, 1954; Vatai et al., 1968; Williams, 1964; McCann and Smith, 1969; MacMahon and Baerg, 1976; Bosch et al., 1977; Baerg, 1983; Schmidt-Ott et al., 1984; Sýkora and Povinec, 1986; Kunze et al., 1990; Nähle et al., 2008). Measurement of ($\text{EC}/{\mathit{\beta }}^{+}$)* for ²²Na is accomplished by measurement of both of the gammas (which come from both the EC* and the ${\mathit{\beta }}^{+\ast }$) and the x-rays (which only come from the EC branch). Relative to the ⁴⁰K ${\text{EC}}_{\mathrm{ground}}/{\mathit{\beta }}^{+}$, the ²²Na (EC/β⁺)* is a more straightforward measurement because of the higher activity (meaning higher count rate) and the higher energy of the x-ray emitted from the Auger electron, which an electron from the same atom that is emitted as a vacancy of an inner shell is filled. In a decay to the excited state of ²²Ne, the de-excitation 1.28 MeV γ will be associated with both electron capture and positron decay. However, those measured 1.28 MeV γ that are not accompanied by two 0.511 MeV annihilation photons can be used to distinguish between both processes. We use the experimental measurements to verify our calculations described above for ⁴⁰K.

Following a similar calculation using the Fermi method, our preferred method, to that used for our proposed estimate of the ⁴⁰K EC${}_{\mathrm{ground}}/{\mathit{\beta }}^{+}$, we estimate an ($\text{EC}/{\mathit{\beta }}^{+}$)* of approximately 0.11. This is within the range of measured values of 0.105–0.115 (Fig. 4), suggesting that our calculation strategy of the ⁴⁰K EC${}_{\mathrm{ground}}/{\mathit{\beta }}^{+}$ is accurate, and lends further confidence to the existence of the current unmeasured ⁴⁰K electron capture to ground-state decay.

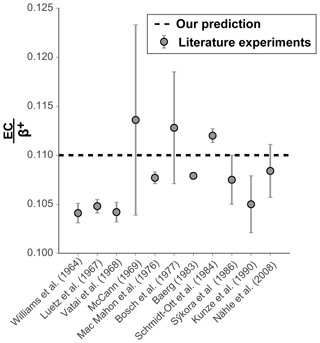
Figure 4 Comparison of experimentally measured ($\text{EC}/{\mathit{\beta }}^{+}$)* ratios of ²²Na (grey circles) adapted from Kunze et al. (1990) with our calculated value (dashed black line). Note the concordance of the theoretical and experimental determinations. The uncertainty in the Baerg (1983) determination is smaller than the symbol.

7 Experimental verification of EC_ground decay mode

In both β⁻ and β⁺ decay, an electron or positron is emitted that allows for direct detection and verification of the decay process. In contrast, electron capture cannot be detected directly. Methods to experimentally verify electron capture rely on indirect processes associated with the rearrangement of the atom following the capture of the orbital electron. Once the electron is captured the atom will rearrange itself to fill the vacancy, resulting in the emission of a characteristic x-ray or Auger electron with an energy defined by the binding energy of the shell vacancy of the daughter nucleus.

In the case of ⁴⁰K, verification of the EC_ground decay can be achieved by measuring the characteristic x-rays (Di Stefano et al., 2017). The orbital electron with the highest probability of capture is from the K-shell; if this electron is captured, the resulting vacancy in the K-shell may be filled by an electron from any of the other shells (e.g., L, M), and a characteristic x-ray is emitted with an energy dependent on the particular shell that fills the vacancy. It is not necessary, however, that all K-capture processes result in the emission of an x-ray. By the Auger effect, a radiationless transfer may occur wherein the K-shell vacancy is replaced by two vacancies in the next outer shell, L, or one in the next two shells; L and M. The energies of the Auger electrons emitted in these transitions depend upon the ⁴⁰Ar product resulting from K-capture. Both electron capture decays to the ground and excited state of ⁴⁰Ar (⁴⁰Ar²⁺) result in the same electron configuration and x-ray emissions. Di Stefano et al. (2017) suggested tagging x-rays with the de-excitation γ associated with electron capture to ⁴⁰Ar²⁺, which has a lifetime on the order of $\sim {\mathrm{10}}^{-\mathrm{12}}$ s (Di Stefano et al., 2017). Measuring these tagged x-rays experimentally will be challenging since it requires identifying a low-probability decay mode with x-ray signals present against a high background from the ⁴⁰Ar²⁺ state. Further, as illustrated in Di Stefano et al. (2020), it is expected that 50 EC* decays occur for every 1 EC_ground decay; therefore, a detector efficiency of ≥98 % is required to make sure that there is fewer than one mis-tagged EC* decay for each true EC_ground decay. The experiment therefore requires an x-ray spectrometer able to resolve the Ar-K x-ray from other x-rays in the background and accurately account for the x-ray–γ-ray coincidence efficiency (≥98 %) to quantify x-ray emission rates in excess of those from the ⁴⁰Ar²⁺ state. Given the complexity involved in this experiment, a pilot study was conducted at SUERC to measure characteristic x-rays from a KCl source. The experiment was not successful because the detector was not able to resolve the Ar-K x-ray sufficiently but demonstrates the potential of this method to detect the x-rays, given a sufficiently high-resolution detector. Full details are provided in the Supplement.

Ongoing attempts are being made to verify this decay mode by careful detection of the characteristic x-rays by the Potassium decay (KDK) experiment (Di Stefano et al., 2017; Stukel, 2018). Experimental verification has implications for (1) rare event physics, as it is a vital component in constraining the irreducible background and verifying results in the DArk MAtter (DAMA) experiment (Pradler et al., 2013); (2) the theory of βdecay (Fermi, 1934), as it is the only third-order unique forbidden electron capture decay known (Audi et al., 2003); and (3) K-Ar and ⁴⁰Ar∕³⁹Ar geochronology, for which it is currently overlooked due to lack of experimental evidence. We further expand on the implications for geochronology below.

8 Relevance for geochronology

Geochronology with the K-Ar system requires either both the branching ratio and the total decay constant, or in the case of an ⁴⁰Ar∕³⁹Ar age wherein the fluence monitor age is constrained independently of its K-Ar systematics (Merrihue and Turner, 1966), only the total decay constant. Using lower and upper bound values of EC${}_{\mathrm{ground}}/{\mathit{\beta }}^{+}$ corresponding to 150 and 212 as described above, the decay constants calculated by Min et al. (2000) (${\mathit{\lambda }}_{{\mathrm{EC}}^{\ast }}=\mathrm{0.580}\pm \mathrm{0.014}\times {\mathrm{10}}^{-\mathrm{10}}$ a⁻¹ and ${\mathit{\lambda }}_T=\mathrm{5.463}\pm \mathrm{0.107}\times {\mathrm{10}}^{-\mathrm{10}}$ a⁻¹), and the ${\mathit{\beta }}^{+}/{\mathit{\beta }}^{-}$ from Engelkemeir et al. (1962) ($\mathrm{1.12}\pm \mathrm{0.14}\times {\mathrm{10}}^{-\mathrm{5}}$), we calculate a β⁺ decay constant of $\mathrm{5.47}\pm \mathrm{0.69}\times {\mathrm{10}}^{-\mathrm{15}}$ a⁻¹ and a range of EC_ground decay constants of 8.2–$\mathrm{11.6}\times {\mathrm{10}}^{-\mathrm{13}}$ a⁻¹. Combining these values with the Min et al. (2000) quantities yields a new partial decay constant for ⁴⁰K to ⁴⁰Ar (${\mathit{\lambda }}_{{}^{\mathrm{40}}\mathrm{Ar}}$) that ranges from 0.588–$\mathrm{0.592}\times {\mathrm{10}}^{-\mathrm{10}}$ a⁻¹ and total decay constant (λ_T) that ranges from 5.471–$\mathrm{5.475}\times {\mathrm{10}}^{-\mathrm{10}}$ a⁻¹. These ranges are within the uncertainties calculated by Min et al. (2000) for decay constants that do not include the EC_ground decay mode. Existing and modified constraints on the decay modes are given in Table 1. Our preferred decay constants are those calculated with the EC${}_{\mathrm{ground}}/{\mathit{\beta }}^{+}=\mathrm{212}$ from Mougeot (2018).

Table 1 Evaluations of decay mode branches and total decay constant used in age determination. ${\mathit{\lambda }}_{{}^{\mathrm{40}}\mathrm{Ar}}$ is the partial decay constant for the ⁴⁰Ar branch, including both the EC* and EC_ground components. Uncertainties from the ${\mathit{\beta }}^{+}/{\mathit{\beta }}^{-}$ and EC${}_{\mathrm{ground}}/{\mathit{\beta }}^{+}$ do not substantially change the uncertainties in ${\mathit{\lambda }}_{{}^{\mathrm{40}}\mathrm{Ar}}$ or λ_T.

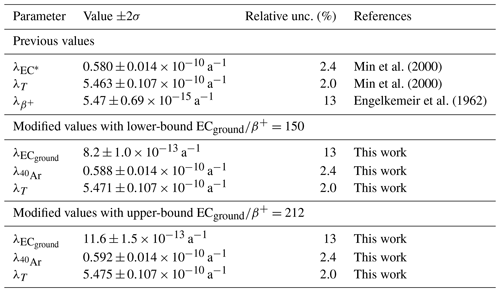
Consequently, K-Ar (and ⁴⁰Ar∕³⁹Ar) ages calculated with these new decay constants will be younger than those calculated using the Min et al. (2000) decay constants. K-Ar dates are most sensitive to shifts in the decay constant because they incorporate the branching ratio, which is more strongly affected than the total ⁴⁰K decay constant. K-Ar ages will decrease by ∼1.4 %–2.0 % at 1 Ma, ∼1.1 %–1.5 % at 1 Ga, and ∼0.6 %–0.8 % at 4.5 Ga (Fig. 5). Ages determined using the ⁴⁰Ar∕³⁹Ar method, for which the fluence monitor age is independently constrained (e.g., Kuiper et al., 2008; Rivera et al., 2011), are much less sensitive to the change in decay constant. Using Eq. (5) from Renne et al. (1998), and assuming calibration to a monitor with an age of 28.2 Ma, ages <28 Ma increase only slightly, by <0.002 %. There is no age difference at 28.2 Ma, the fluence monitor age. Ages then decrease for ages >28.2 Ma, with ages decreased by 0.07 %–0.10 % at 2.5 Ga, and by 0.09 %–0.13 % at 4.5 Ga (Fig. 5).

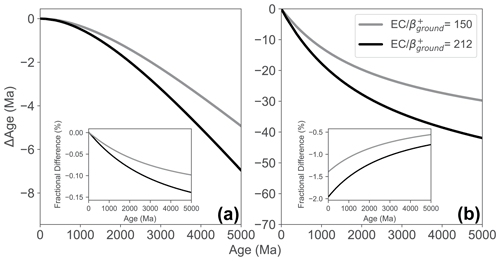
Figure 5 Change in age, Δage, is the age of a given sample with the decay mode to ground state included, subtracted from the age with the decay mode to ground state omitted. Panel (a) shows the change in age using the ⁴⁰Ar∕³⁹Ar equation with independently calibrated standards using both the lower bound ($\text{EC}/{\mathit{\beta }}^{+}=\mathrm{150}$; grey) and upper bound ($\text{EC}/{\mathit{\beta }}^{+}=\mathrm{212}$; black). Panel (b) shows the change in age using the K-Ar equation using both the lower bound ($\text{EC}/{\mathit{\beta }}^{+}=\mathrm{150}$; grey) and upper bound ($\text{EC}/{\mathit{\beta }}^{+}=\mathrm{212}$; black). Inset figures in each panel show the fractional differences in age by the inclusion of both the upper- and lower-bound $\text{EC}/{\mathit{\beta }}^{+}$ value. The larger difference in ages for the K-Ar system is due to the dependence on both the total decay constant and branching ratio.

The age of fluence monitors such as the Fish Canyon tuff sanidine (e.g., Morgan et al., 2014) determined by intercomparison with astronomically tuned ages of ash beds (Kuiper et al., 2008; Rivera et al., 2011) is also sensitive to revision of decay constants. Using the data published by Kuiper et al. (2008), and incorporating an EC_ground decay mode, we calculate a new age for Fish Canyon sanidine of 28.200±0.044 Ma, nominally lower but indistinguishable from the published value of 28.201±0.044 Ma. Overall, the effects of an EC_ground decay mode are unlikely to be significant for most current applications of ⁴⁰Ar∕³⁹Ar geochronology. However, given the levels of analytical precision attainable by the K-Ar dating approach when dating geologically recent materials by K-Ar (e.g., Altherr et al., 2019), the EC_ground decay mode will impact the accuracy of this chronometer.

9 Conclusion

The Fermi theory of β decay has decades of experimental support and is well established. We demonstrate this here by using these theories to accurately calculate the decay rate of a ²²Na, a nuclide with an experimentally verified decay rate. We have used this information to demonstrate the high likelihood that the suspected second electron capture decay mode of ⁴⁰K exists. Based on the calculations of Mougeot (2018), the best estimate of the partial decay constant for ⁴⁰K direct to ground-state ⁴⁰Ar is $\mathrm{11.6}\pm \mathrm{1.5}\times {\mathrm{10}}^{-\mathrm{13}}$ a⁻¹ (2σ), and other calculations are no lower than about $\mathrm{8.2}\times {\mathrm{10}}^{-\mathrm{13}}$ a⁻¹. Combining this with the decay constants published by Min et al. (2000) results in revised values of ${\mathit{\lambda }}_{{}^{\mathrm{40}}\mathrm{Ar}}=\mathrm{0.592}\pm \mathrm{0.014}\times {\mathrm{10}}^{-\mathrm{10}}$ a⁻¹ and ${\mathit{\lambda }}_T=\mathrm{5.475}\pm \mathrm{0.107}\times {\mathrm{10}}^{-\mathrm{10}}$ a⁻¹. This addresses a long-standing question in K-Ar and ⁴⁰Ar∕³⁹Ar geochronology and provides future workers with confidence that the ⁴⁰K EC_ground decay mode exists. Just as important as providing support for its existence, we also demonstrate that the magnitude of this decay mode is small enough that neglecting it has not yet resulted in significantly biased geochronological ⁴⁰Ar∕³⁹Ar data. The same cannot be stated for the K-Ar dating approach, especially for geologically young materials.

Despite the strong grounding in theory, the EC_ground decay mode has yet to be detected. The next step is experimental verification to determine the branching ratio. This will allow for a more complete evaluation of uncertainties associated with the decay mode and the branching ratio. This experiment is difficult but not intractable.