the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
A revised alpha-ejection correction calculation for (U–Th) ∕ He thermochronology dates of broken apatite crystals
Peter W. Reiners
Accurate corrections for the effects of alpha ejection (the loss of daughter He near grain or crystal surfaces due to long alpha stopping distances) are central to thermochronometry. In the case of apatite dating, alpha-ejection correction is complicated by the fact that crystals are often broken perpendicular to the c axis. In such cases, the correction should account for the fact that only some parts of the crystal are affected by alpha ejection. A common current practice to account for such broken crystals is to modify measured lengths of broken crystals missing one termination by a factor of 1.5, and those missing both terminations by a factor of 2. This alpha-ejection “correction correction” systematically overestimates the actual fraction of helium lost to alpha ejection, and thus overcorrects the measured date relative to that determined for an otherwise equivalent unbroken crystal. The ratio of the alpha-ejection-affected surface area to the volume of a fragmented crystal is equivalent to the surface-area-to-volume ratio of an unbroken crystal that is either twice as long (for fragments with one termination) or infinitely long (for fragments with no termination). We suggest that it is appropriate to revise the fragmentation correction to multiply the lengths of crystals missing one c-axis termination by 2, and those missing both c-axis terminations by some large number ≳20. We examine the effect of this revised correction and demonstrate the accuracy of the new method using synthetic datasets. Taking into account alpha ejection, the rounding of the He concentration profile due to diffusive loss, and the accumulation of radiation damage over a range of thermal histories, we show that the revised fragmentation alpha-ejection correction proposed here accurately approximates the corrected date of an unbroken crystal (“true” date) to within <0.7 % on average (±4.2 %, 1σ), whereas the former method overcorrects dates to be ∼3 % older than the “true” date on average. For individual grains, the former method can result in dates that are older by a few percent in most cases, and by as much as 12 % for grains with aspect ratios of up to 1:1. The revised alpha-ejection correction proposed here is both more accurate and more precise than the previous correction, and does not introduce any significant systematic bias into the apparent dates from a sample.
Please read the corrigendum first before continuing.
-
Notice on corrigendum
The requested paper has a corresponding corrigendum published. Please read the corrigendum first before downloading the article.
-
Article
(3255 KB)
- Corrigendum
-
Supplement
(894 KB)
-
The requested paper has a corresponding corrigendum published. Please read the corrigendum first before downloading the article.
- Article
(3255 KB) - Full-text XML
- Corrigendum
-
Supplement
(894 KB) - BibTeX
- EndNote
Since the development of modern apatite thermochronometry, the technique has become a versatile and powerful tool for a range of geological problems (Zeitler et al., 1987; Farley et al., 1996; Flowers et al., 2022a, b). To fully leverage the power of the technique, however, it is necessary to account for the wide range of possible complications that commonly cause data dispersion to be greater than analytical errors. Of particular significance is correcting for the loss of daughter nuclides due to the problem of alpha ejection. Apatite He dating uses the accumulation of daughter nuclide 4He (i.e., alpha particles) from the spontaneous alpha decay of 238U, 235U, and 232Th (as well as a minor contribution from 147Sm) to constrain possible thermal histories of samples, which is sometimes simplified as providing a date of cooling through some closure temperature (∼ 30–90 ∘C) at which helium diffusion out of a crystal is sufficiently slow for the system to be considered closed. However, this method is complicated by the fact that the sizes of most typical apatite crystals are only several times greater than the stopping distance of alpha particles (∼20 µm), meaning that the fraction of 4He ejected from a crystal must be accounted for in most applications (Farley et al., 1996).
Careful measurement of crystal geometries allows accurate approximation of the cumulative alpha-ejection loss of helium from a crystal (Ziegler, 1977; Farley et al., 1996; Farley, 2002; Hourigan et al., 2005; Ketcham et al., 2011; Reiners et al., 2018). Because the likelihood of an alpha particle being ejected from a crystal is directly related to the parent nuclide's proximity to the crystal surface, the fraction of helium retained in the crystal (FT) is a function of the crystal's surface-area-to-volume ratio (β) (Farley et al., 1996). In the simplest case of a spherical grain with a homogeneous parent nuclide distribution, FT is a cubic polynomial function of β (Farley et al., 1996). FT can be estimated for other geometries using a polynomial function calibrated by Monte Carlo alpha-ejection models (Farley, 2002; Ketcham et al., 2011). In practice, a parent-nuclide-specific is determined and a corrected date can be calculated by incorporating it into the full decay equation:
where t is the unknown variable that must be solved numerically or iteratively; the 4He, 238U, 235U, 232Th, and 147Sm contents are measured; λi is the decay constant for the given isotope; and is the alpha-ejection correction factor for the given isotope, calculated from the crystal geometry (Ketcham et al., 2011). A more approximate corrected date can also be calculated by simply dividing the measured (raw) date by FT (Farley and Stockli, 2002), though this is less accurate for older dates.
These calculations generally assume the ideal case of a euhedral, prismatic crystal with a homogeneous parent nuclide distribution, entire original crystal faces, and insignificant parent nuclide concentrations outside and within one alpha stopping distance of the exterior of the crystal during the interval in which temperature was low enough to accumulate He. When these assumptions are violated, further adjustments to the standard FT correction are required.
If information about the magnitude and pattern of parent-nuclide zonation is available, an adjusted FT may be applied to account for an inhomogeneous parent-nuclide distribution (Hourigan et al., 2005; Farley et al., 2011; Ault and Flowers, 2012; Gautheron et al., 2012). Absent such information, as is the case in most routine analyses, use of the standard unzoned correction assuming a homogeneous distribution of the parent nuclide would introduce errors that skew the crystal's apparent date to be younger if its rim is enriched in parent nuclides, and older if it is depleted in parent nuclides (Farley et al., 1996; Hourigan et al., 2005). For apatite, these errors are usually minor (<1.5 % for 80 % of apatite crystals and <9.5 % for 95 %), because apatite crystals in most cases do not typically exhibit extreme zonation of parent nuclides (Ault and Flowers, 2012, in the case of old cratonic samples). The data from that study suggest that the errors are usually symmetrically distributed, with apatite populations not exhibiting a bias towards either rim-enriched or rim-depleted grains, though this may not be the case for rocks that experienced metamorphism or hydrothermal alteration. Accounting for the effects of He implantation from sources external to the grains is not typically possible for grains separated from their petrographic context, although in some cases particular date–eU (effective uranium concentration) or date–Rs (sphere-equivalent radius) correlations may be used to interpret such effects (Spiegel et al., 2009; Murray et al., 2014).
The focus of this paper is the adjustment to the FT correction that should be made in the case of crystals that are broken perpendicular to the c axis, as is common for apatite, whether during mineral separation or during erosion and transport (if the fragmentation post-dated cooling). If errors due to fragmentation are large, they can significantly impede our ability to extract geologically meaningful information from dates calculated from parent–daughter nuclide ratios. Broken and morphologically suboptimal crystals are frequently analyzed, particularly when the quality of mineral separates is poor and/or the apatite yield from a sample is low. In addition, imperfect basal (0001) cleavage in apatite (Dana, 1963; Palache et al., 1963) leads to the fact that many dated crystals are broken perpendicular to their c axis and lack original terminations, even for high-quality samples. A common strategy is to apply a fragmentation correction to the FT calculation, which accounts for the fact that the fracture exposes surface area where alpha ejection did not occur (Farley, 2002). This correction seeks to approximately correct for the originally greater length of the unbroken apatite crystal by multiplying the length of all broken crystals by 1.5 (if one end is broken) or 2 (if both ends are broken) (Farley, 2002; Farley et al., 1996; Brown et al., 2013; Beucher et al., 2013; Reiners et al., 2018). Though it is not possible to find the original lengths of broken crystals, Farley (2002) argued that these approximations are sufficient because FT is relatively insensitive to the length of the crystal.
An alternative approach to this problem is that of Brown et al. (2013), who argued that, for interpreting thermal histories, it is best to leave dates uncorrected and instead evaluate the variation in date among crystals with different morphologies and numbers of broken ends. If one assumes that breakage occurred prior to cooling to temperatures of partial He retention, the raw (uncorrected) dates of broken crystals can vary by up to 60 % for certain t-T (time-temperature) histories, and, for sufficiently large datasets of fragmented crystals, considering the patterns of dispersion in uncorrected dates can constrain the thermal history (Brown et al., 2013). In practice, however, FT-corrected dates remain widely reported, partly because correcting for alpha ejection and fragmentation is necessary to compare dates to other datasets and dates of geologic significance. A more accurate correction would allow both broken and unbroken crystals within a sample and across samples to be appropriately compared without introducing additional systematic bias.
Although the conventional fragmentation correction has been widely applied, its accuracy and precision have not been demonstrated. In the first part of this paper, we consider the rationale behind the early approach, propose a revision, and compare the results of both methods. We test the new method using synthetic data and demonstrate the accuracy of the revised correction. We take into account a range of broken crystal sizes, the number of terminations present, and various thermal histories and their associated effects on helium diffusivity, and we quantify the uncertainty that can be attributed to the fragmentation correction alone. Considering the numerous natural sources of uncertainty in apatite He dating, achieving greater confidence in the accuracy of the fragmentation FT correction and minimizing its uncertainty ultimately aids in the interpretation of other possible sources of uncertainty and errors (He et al., 2021).
For an idealized spherical grain, the alpha-ejection correction is a function of the radius of the sphere (R) and the alpha stopping distance for the given parent nuclide (S):
(Farley et al., 1996). Where R≫S, the function approaches a linear relationship:
(Farley et al., 1996), where β is the ratio of the surface area of the crystal to its volume. In other words, the fraction of helium lost due to alpha ejection near the crystal surface is approximately a function of the ratio of the surface area of a crystal to its volume. Considering more realistic crystal geometries, polynomial equations that define the value as a function of β have been empirically determined using Monte Carlo simulations for each parent nuclide i and its respective alpha stopping distance (Farley et al., 1996; Hourigan et al., 2005). For hexagonal prisms, simply measuring the length (L) and radius or half-width of the cylindrical prism (R) allows the computation of β:
The general idea behind modified FT corrections is to modify β under the assumption that the polynomial functions relating β and FT are nearly identical for similar geometries (e.g., a hexagonal prism with bipyramidal or pinacoidal terminations). This was the approach taken to correct for the lost crystal surface in the case of crystals polished parallel to the c axis (Reiners et al., 2007). In the case of c-axis-perpendicular breakage, the Farley et al. (1996) approach sought to establish the length of the original, unbroken crystal. Because it was observed that the corrected-length-to-radius ratios of most apatite crystals (5:1) were sufficiently high that the FT corrections become largely independent of length, it became standard practice at most laboratories to simply modify β by multiplying the lengths of broken crystals by arbitrary factors of 1.5 or 2, thereby modifying FT (Farley et al., 1996; Farley, 2002). Alternatively, in the slightly different context of the inverse modeling of a large set of uncorrected ages, Beucher et al. (2013) suggested that a rule of thumb for predicting the unknown initial length should be to add the maximum fragment length of a set of fragments and two times the maximum radius. To the first order, guessing the unknown initial length using consistent factors such as these suffices to roughly account for the loss of alpha-ejection-affected surface area at the tips; this is because, as L increases, the increase in surface area of a crystal is less than that of the volume, in effect reducing β.
In detail, however, the fraction of helium remaining in a fragmented crystal does not depend on the unknown (and precisely unknowable) initial length. Rather, it should be directly related to the surface area of the broken crystal that was originally affected by alpha ejection. Assuming that we can identify when crystals have lost one or both terminations, that the breakage generally occurs more than one average alpha stopping distance from the tip, and that diffusion has not significantly modified the daughter concentration profiles, the ratio of alpha-ejection-affected surface area to volume (βα) could be simply calculated by measuring and then subtracting the surface area of the broken face(s) from the total surface area. For a hexagonal prism, simple geometric calculations demonstrate that the βα values of singly and doubly broken crystals are equivalent to the β of an unbroken crystal of the same width that is twice as long or infinitely long, respectively; this is shown graphically in Fig. 1. Consider that the helium profile in an unbroken crystal is symmetrical, such that when the crystal is broken in half. Each half will have the same fraction of helium remaining (FT); thus, conversely, any broken crystal with one termination (with the breakage occurring more than one alpha stopping distance from the tip) has the same FT as a hypothetical unbroken crystal double its length. For crystals with no terminations remaining, any c-axis-perpendicular segment or cross section of the crystal will have the same FT, no matter its length or its position along the fragment; therefore, fragments with no terminations have the same FT as an infinitely long unbroken crystal, where the terminations, which have a different FT, have a vanishingly small effect on the overall FT of the crystal.
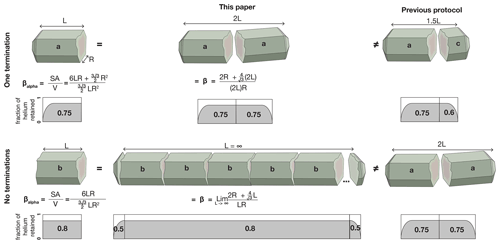
Figure 1The ratio of alpha-ejection-affected surface area to volume, or βα, of a broken crystal that has lost a basal fragment longer than one alpha stopping distance is equivalent to the surface-area-to-volume ratio of an unbroken crystal that is either twice as long (for fragments with one termination) or infinitely long (for fragments with no termination). The simple geometric calculations shown assume a flat hexagonal termination, but they apply by the same logic to any geometry, regardless of the shape of its body (e.g., cylindrical, tetragonal, or hexagonal) or the shape of its terminations (e.g., pyramidal, flat, or rounded). The profiles of fraction of helium retained that are shown below each fragment are schematic and serve only to illustrate the equivalence or non-equivalence of fragments of different lengths (e.g., a=0.75, b=0.8, c=0.6), and do not correspond to any specific dimensions. As discussed in the text, these calculations assume no change to the daughter concentration profile due to diffusion.
It follows, then, that a more accurate fragmentation correction that explicitly considers the lost surface area of a broken crystal should be to multiply the length of a broken crystal by 2 or some large number (to simulate the limit as L approaches infinity), respectively, rather than 1.5 or 2; i.e.,
where L is the measurement of the crystal dimension perpendicular to the fracture (since crystals commonly break perpendicular to the c axis in apatite crystals, L should usually be measured parallel to the c axis, even if it is shorter than the width). In the unlikely case of an oblique fragment, L should be the average of the longer and shorter sides. This simple correction has the benefit of applying to other geometries, regardless of the shape of the body (e.g., cylindrical, tetragonal, or hexagonal) or the shape of its terminations (e.g., pyramidal, flat, or rounded): the βα of any singly broken crystal is equivalent to the β of a whole crystal twice its length, and the βα of any doubly broken crystal is equivalent to the β of a whole infinitely long crystal. The correction can thus be applied to all crystals broken perpendicular to the c axis, regardless of original length, and only requires knowledge of the width and length of the broken crystal and the number of terminations present. Similarly, this correction can be applied to zircon fragments using the appropriate beta equation (though it is less common to see zircon fragments with only one termination or no terminations). We emphasize that though this fragmentation correction is similar in form to that of Farley (2002) in that it involves length-modifying factors, it differs in that it seeks to approximate the length of a whole crystal with the same fraction of helium remaining as the fraction remaining in the broken fragment, rather than seeking to approximate the unknown length of the original unbroken crystal.
To characterize the uncertainty of the new and old protocols, we applied the above fragmentation correction equations to a synthetic dataset of raw (uncorrected) dates of broken prismatic crystals where the corrected dates of the original unbroken crystals were known. Note that, as a simplification, a length-modifying factor of 20 was used to approximate the limit to infinity (see Sect. 4.1). To facilitate comparison of the results from the new and old protocols, we used the same datasets of raw uncorrected dates from Brown et al. (2013), which were generated from the volume-integrated 4He concentration in a random set of crystal fragments broken at varying positions along the original crystals (Beucher et al., 2013). We assumed uniform spatial distributions of the parent nuclide and applied both protocols to all fragments exactly as we would calculate FT-corrected dates in routine laboratory analyses; i.e., we assumed no knowledge of the original length and thermal history of each crystal to compute the corrected age, and we used only the raw date, the length and width of the broken crystal, and the number of terminations present for the calculation. We then compared the FT-corrected dates of the synthetic fragments with the known FT-corrected date of the corresponding unbroken crystals. The original unbroken crystals from which the fragments were generated had the same geometry (a hexagonal prism 400 µm long and 150 µm wide), and each experienced one of five different representative thermal histories (rapid monotonic cooling; slow monotonic cooling; prolonged isothermal residence in the partial retention zone followed by rapid cooling; a mix of slow cooling and isothermal holding in the partial retention zone; or gradual reheating (e.g., burial) followed by rapid cooling; see Wolf et al., 1998).
To test the accuracy of the proposed protocol under the stated ideal assumptions (that the fragmentation has occurred more than one average alpha stopping distance from the tip, and that there is no significant diffusion-induced modification of the helium concentration profile), we excluded any randomly generated crystals broken <20 µm from the tip and included only fragment sets that experienced the two thermal histories (monotonic cooling) associated with the least amount of diffusive modification of the helium profile (Fig. 2a). To approximate the actual circumstances under which fragments are analyzed in laboratories, where we have no a priori knowledge of the thermal history and cannot readily discern where a crystal has broken, we included the full fragment dataset (Fig. 2b). 23 % of the randomly generated fragments in that dataset were broken within ∼20 µm from the tip, and 60 % experienced complex thermal histories involving reheating or extended residence in the partial retention zone.
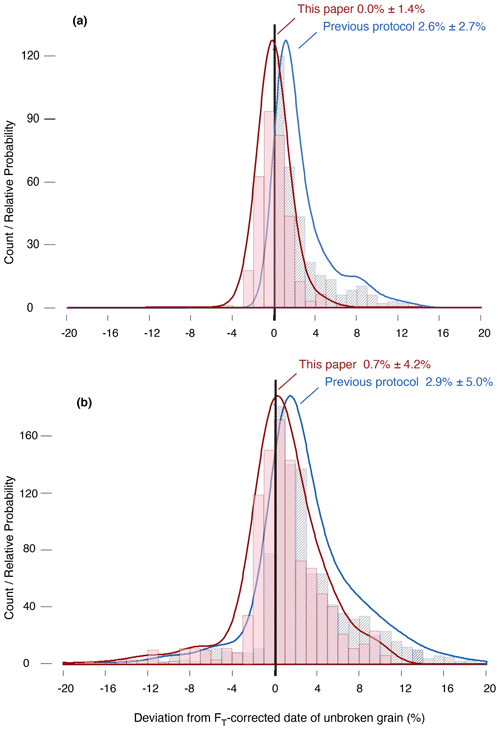
Figure 2Histograms and kernel density estimate (KDE) functions comparing the results of applying the new protocol suggested in this paper (red) with the results of applying the previous protocol (blue) to a synthetic dataset of raw, uncorrected dates (n=1000, see Brown et al., 2013). The error is defined to be the % deviation of the FT-corrected dates of a broken crystal from the FT-corrected date of the whole crystal, which is known because the synthetic fragments are generated from a whole crystal with a known “age”. The new protocol is more accurate and more precise at correcting for the effect of fragmentation, both in the ideal case (a) assuming that fragmentation has occurred more than one average alpha stopping distance from the tip and that there is no significant diffusive modification of the helium profile, as well as in the more realistic scenario (b), which includes corrected dates from fragments that are broken close to the tip and fragments that experienced thermal histories leading to significant diffusive modification in addition to the dates contained in (a). Annotations show the mean ± standard deviation (1σ); KDE functions are normalized to the same peak height.
The new protocol accurately corrects for the effect of fragmentation, deviating by 0.0 %±1.4 % (1σ) from the corrected date of the unbroken crystal, under the ideal assumptions stated above (Fig. 2a). By comparison, under the same assumptions, the old protocol leads to corrected dates that are almost all too old, on average by 2.6 %±2.7 %. When the two assumptions are not met, the proposed fragmentation correction results in a broader range of uncertainty (), but it is nevertheless more accurate and more precise than the old protocol () (Fig. 2b). Using the new protocol, only 3 % of the corrected dates deviate from the corrected date of the unbroken crystal by greater than 10 %; this represents a 66 % reduction relative to the prior protocol.
4.1 Difference between corrections for different crystal dimensions
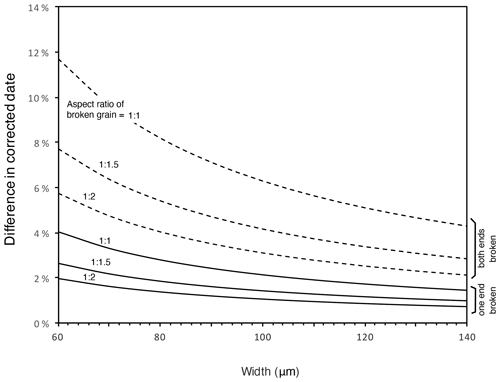
Though multiplying a fragment length by different factors may seem to be a minor revision, the resulting difference in corrected dates is not negligible. This is partly because the observation that FT correction is not strongly dependent on length, upon which the fragmentation correction was initially based, does not hold true for the smaller crystals commonly analyzed today (e.g., c-axis-perpendicular width < 150 µm). Figure 3 shows the effect of crystal length (or modified crystal length, as used in the calculation of β or βα) on the inverse value of FT, an approximation for the correction's effect on the final reported date (Fig. 3). Since both protocols effectively multiply the length of a broken crystal to compute an adjusted FT value, the inverse FT values of the new and old protocols for any given crystal width all lie on the same curve for FT as a function of length (normalized to width). Particularly when the length of a broken crystal is close to its width, and when the width is small, the FT correction is not independent of the modified length. For example, for a singly broken crystal that is 60 µm in width and equally long (the minimum dimensions of crystals routinely analyzed in our lab), the difference between the new and old protocols would be 4 %; for a doubly broken crystal of the same dimensions, the difference would be 12 % (Fig. 4). The overcorrection of the previous protocol could be even larger for drum-shaped fragments (i.e., crystals broken on both ends and shorter in c-axis-parallel length than width). For a broken crystal that is 140 µm in both width and length, the difference would be 2 % and 5 % for singly and doubly broken crystals, respectively. The magnitudes of these differences are not negligible, at least relative to other sources of error in FT corrections. By comparison, for example, the updated alpha-ejection models of Ketcham et al. (2011) based on revised alpha stopping distances affect dates by approximately 1 %–5 %, and 2D measurement of the crystal geometry introduces errors of ∼2 % (Cooperdock et al., 2019).
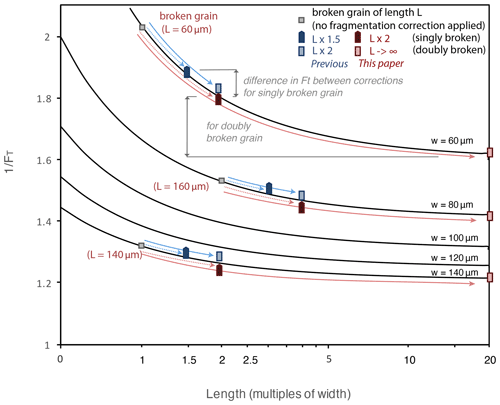
Figure 3The inverse of the FT value plotted as a function of crystal length L, as used in the calculation of β or βα. For a broken crystal, this is measured parallel to the c axis (as a multiple of width) and modified by some factor (see legend). The inverse of FT can be approximately considered a multiplier for the raw date, where corrected date ≈ raw date (Farley et al., 1996). Inverse FT corrections for three example fragments are shown (width = 60, 80, and 140 µm and length = 60, 160, and 140, respectively) with the corresponding fragment-corrected FT values for singly or doubly broken crystals. The gray squares indicate the actual length of the fragment and show their inverse FT values if no fragmentation correction is applied. For convenience, the asymptotic value is assumed to be approximately the same as multiplying by some large number (e.g., 20). Note that, strictly speaking, the calculation of a corrected date requires using the full decay equation with an individual for each nuclide, rather than the simplification of corrected date ≈ raw date .
4.2 Uncertainty in fragmentation correction compared to other sources of date dispersion
In the ideal case (i.e., the fragmentation has occurred more than one average alpha stopping distance from the tip and there is no significant diffusion-induced modification of the helium concentration profile), we have shown that the proposed fragmentation correction is both accurate and precise ( %). When these ideal assumptions are not met, the uncertainty increases (± 4.2 %) (Fig. 2b). The larger uncertainties are largely due to the diffusive modification of helium profiles. In our test of this protocol, all cases of corrected fragment dates that deviate by more than >5 % from the corrected date of the unbroken crystal can be attributable to thermal histories involving prolonged residence in the partial retention zone (Fig. 5). Without a priori knowledge of the sample's thermal history, this is a problem for the new fragmentation correction just as it is for the old protocol, because the calculation of FT correction only assumes loss of helium due to alpha ejection. The additional uncertainty associated with the fragmentation correction fundamentally relates to the fact that using βα to correct FT implies taking the lost surface area (“skin”) affected by alpha ejection as a proxy for the lost volume (the outer “shell”) of the crystal affected by alpha ejection.
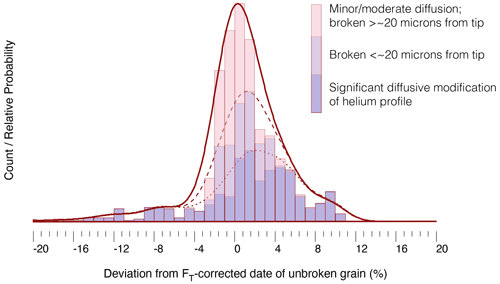
Figure 5Uncertainty associated with the proposed fragmentation correction due to inclusion of fragments broken too close to the tip (dashed) and due to thermal histories that involve significant diffusive modification of the helium profile (dotted). The histogram and curves are stacked and cumulative, such that the dashed probability curve includes both close-to-tip fragments as well as fragments with significant diffusive loss.
We emphasize that because the FT-corrected dates of the fragments are compared to the FT-corrected date of the whole crystal, Figs. 2 and 5 assess the effect of the brokenness correction alone. Parent-nuclide zonation, eU variation, and diffusive helium loss remain important sources of additional error and dispersion (e.g., Meesters and Dunai, 2002; Herman et al., 2007; Gautheron et al., 2012; Brown et al., 2013; Beucher et al., 2013). Notwithstanding the effects of date variation due to all these effects, the fragmentation correction proposed in this paper more consistently and accurately reproduces the FT-corrected date of the unbroken crystal. An illustrative case is that of a hypothetical date-elevation transect from a crustal block that cooled slowly through the partial retention zone until some point in time, then subsequently experienced very rapid cooling (from Brown et al., 2013). A key observation of Brown et al. (2013) was that the large dispersion of raw uncorrected fragment dates is due to the fact that these dates can be both younger and older than the whole crystal, and that fragments of the same length can yield different dates, while, conversely, fragments of different lengths can yield the same date. The dispersion is compounded because slow cooling leads to significant diffusive modification of the helium profile in a crystal. Despite this large dispersion of uncorrected fragment dates (up to 60 %), and despite variations in eU and grain sizes, applying the new fragmentation correction introduces limited uncertainty relative to the dispersion caused by other effects (Fig. 6). This facilitates the interpretation of widely dispersed data by reducing the number of variables that must be considered, and demonstrates the utility of applying a fragmentation correction when analysis of the pattern of dispersion in > 20–30 crystals is not practical. Finally, while both the new and old FT correction for broken crystals reliably approximates the corrected date of an unbroken crystal for a range of eUs and crystal sizes, the new correction reduces the systematic bias that is introduced by the old protocol when many broken crystals are analyzed in a sample by ∼ 3 %–4 % (Fig. 6).
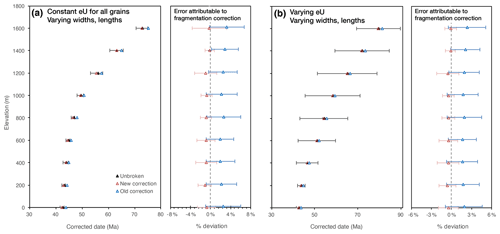
Figure 6(a) Date-elevation transect of a crustal block that cooled slowly through the partially retention zone and was subsequently rapidly exhumed (see Brown et al., 2013, Fig. 9), showing fragment dates corrected using the new protocol (red) and the previous protocol (blue), and the expected whole-crystal date (black). Note that the red and black triangles may be difficult to distinguish because they overlap in most cases. Corrected dates are from fragments of varying lengths, both singly and doubly broken, that were generated from crystals with variable widths and lengths but constant eU. Error bars in the date-elevation transect represent intra-sample date dispersion and are shown for the new protocol only. Error bars in the right panel show the % deviations of the fragment dates corrected using the new (red) and old (blue) protocol from their corresponding corrected whole-crystal dates. (b) Same as (a), but the fragments were generated from crystals of varying eU (15–100 ppm, Brown et al., 2013), in addition to varying width and length. Notice that the introduction of eU as a variable significantly increased the intra-sample dispersion of corrected dates, but that the error attributable to the fragmentation correction alone was not materially affected. All error bars are 1σ.
Ultimately, the characterization of the uncertainty due to the application of the fragmentation correction moves us one step closer to a more comprehensive quantification of all the uncertainty involved with apatite He dating (Fig. 7). Previous work has already shown, for example, that
-
Size- and eU-dependent diffusivity can cause apparent dates to systematically vary (Reiners and Farley, 2001; Flowers et al., 2009; Whipp et al., 2022).
-
The presence of extraneous daughter nuclides whose parent nuclides are not accounted for can cause outlier dates many multiples older than the true date (4He-rich fluid inclusions; U- or Th-rich inclusions or microinclusions where the inclusions are not fully dissolved; grain boundary phases or adjacent grains that contribute helium to the grain but are not in the analyzed aliquot) (Spiegel et al., 2009; Fitzgerald et al., 2006; Murray et al., 2014).
-
A nonuniform distribution of the parent nuclides (i.e., “zonation”) can cause dates to be both older or younger by <1.5 % in most cases. Even if zonations are not accounted for, the probability distribution of errors due to zonations can be approximated by either examining a representative selection of apatite in a sample or using a reference compilation (e.g., Ault and Flowers, 2012) (Fig. 7a).
-
Technician-to-technician differences in 2D grain measurement cause date variations that differ by ∼2 % from corrected dates computed using actual 3D geometry (Cooperdock et al., 2019).
A future step towards a more rigorous evaluation of the uncertainty of analyses of individual grains or of multiple analyses from a single sample as a whole could involve the propagation of each of these uncertainties to account for sample- and grain-specific information such as the probability of implantation (approximated from the spatial distribution of heavy minerals in a sample, obtained via X-ray computed tomography), the probability of extreme parent-nuclide zonations in a sample (based on fission track mounts) or from a reference compilation, and whether fragments were analyzed. The resulting distribution (e.g., Fig. 7d) would then represent the sample-specific probability of single-aliquot apatite He dates. For larger datasets, especially in the case of larger-n analyses (e.g., Fig. 7e), this would provide a more robust rationale for the interpretation of the geologically significant date. For smaller datasets, the expected distribution would inform our selection of the appropriate summary statistic to represent the date variation in a given sample (He et al., 2021).
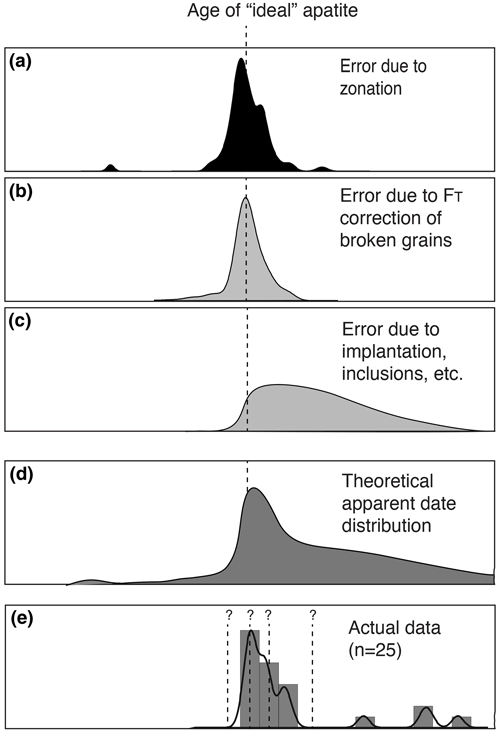
Figure 7Illustration of how uncertainties due to different complications in apatite helium dating – e.g., uncertainty due to zonation (a), uncertainty due to the correction for broken crystals (b), and error due to implantation and other effects (c) – could together be combined to form a theoretical apparent date distribution (d) that would inform our interpretation of real data and the choice of the appropriate summary statistic (whether the minimum, mean, median, or peak date) for representing a sample's date. Note that (a) is based on actual data from Ault and Flowers (2012) and (b) is based on this study, whereas (c) is schematic. The last panel, (e), is a representative sample (n=25) that shows the expected non-normal and right-skewed distribution from an actual large-n sample (He et al., 2019; Thomson et al., 2019). The peak date in this case would likely approximate the date of an “ideal” apatite, but a full accounting of the probability of various uncertainties would provide a more robust rationale for that interpretation.
4.3 Timing of fragmentation
Finally, we emphasize that whether or not to apply the fragmentation correction in the first place is a decision that precedes the choice of the protocol. For non-detrital samples, any crystals with existing fractures prior to cooling would most likely still be intact from an alpha-ejection perspective (i.e., the fragments are immediately adjacent, such that He is implanted across fractures). This means that the fragmentation correction would still need to be applied to a crystal that has lost one or two termination(s) even if a fracture was present before cooling. On the other hand, the question of when the fracture occurred matters for He diffusion. Depending on the thermal history, and whether the fracture pathway was a free surface for He loss, the He concentration profile of the fragment would be the result of some combination of alpha ejection having acted on external nonfragmented surfaces and diffusion having acted on all free surfaces. An additional complication for certain thermal histories (e.g., partially reset samples) is that a broken face that is still adjacent to the other broken side (so that it has not experienced alpha-ejection helium loss) may experience more diffusion at this fracture plane than the exposed external faces where diffusion is inhibited by the lower He concentration at the crystal boundary.
For detrital samples, the situation is more complicated. The accuracy of the protocol proposed above, as with the previous fragmentation protocol, is founded upon the assumption that fragmentation occurred recently relative to the timing of cooling. This is not always straightforward to assess. For samples such as modern river sands derived from crystalline rocks, an assumption that c-axis-perpendicular breakage occurred after cooling (approximately below the closure temperature) can be reasonably based on textural clues, particularly the contrast between detrital apatite grains that are rounded or abraded by transport and the sharp faces and corners of fragment surfaces that have not. For sedimentary samples that have not been clearly buried and reset, e.g., sedimentary rocks not buried more than couple of km, the timing of fragmentation would be more ambiguous, unless the age of the deposition is known (assuming that the age of the deposition is close to the age of erosion and transport, and therefore the timing of fragmentation).
Analogous to the problem of the unknown timing of abrasion for rounded detrital apatite and zircon grains (Rahl et al., 2003; Thomson et al., 2013; Reiners et al., 2018), if the timing of fragmentation is unknown, we could define a maximum date Afc, the FT-corrected date without fragmentation correction, corresponding to fragmentation before or immediately after cooling; and a minimum date Affc, the fully FT-corrected date with fragmentation correction, corresponding to fragmentation during laboratory mineral separation. If there is sufficient geologic context, we can take the date of the sediment As to be the latest time at which the fragmentation occurred, such that the minimum date, Amin, would instead be
A conservative approach would then be to display a “plot date” that is the mean of the maximum and minimum possible dates, and an error bar depicting the possible range of dates (Thomson et al., 2013).
In the case of detrital samples for which the timing of fragmentation is unknown, and that have also experienced non-monotonic cooling so that there has been significant diffusive loss after fragmentation (e.g., a fragment in a sedimentary rock that has been partially reset by burial-induced heating), fragmentation-corrected dates will be systematically younger than the corrected dates of whole, unbroken grains. For example, the corrected dates of any whole crystal may reflect a date–Rs (sphere-equivalent radius) relationship, and naively applying the fragmentation correction to fragments will lead to corrected dates that all lie below this the corrected date–Rs relationship of unbroken crystals. In this case, a plot date and the corresponding maximum and minimum dates could still be calculated, as defined above The plot dates would reflect a similar date–Rs relationship: i.e., if fragmentation occurred soon after cooling and significantly before partial reheating, the maximum date Afc would be the closest to the corrected date of an equivalent unbroken grain (except that it would be younger than the equivalent unbroken grain to the extent that the unbroken grain is less affected by diffusion due to its size). To consider the date–size relationship of fragments, it would be necessary to either calculate an assumed sphere-equivalent radius () using the half-width and an assumed aspect ratio for typical ratios, or to use a sphere-equivalent radius based on FT (see Cooperdock et al., 2019), using the fragment's alpha-ejection-affected-FT value proposed here. The rationale for the latter option would be analogous to the case of the fragmentation FT correction: the ratio of the alpha-ejection-affected surface to the volume of a broken crystal is a good proxy for the ratio of the available-for-diffusion surface to the volume.
In all cases where significant diffusive loss complicates the application of the fragmentation correction, the best way to approach the problem may be to consider a combination of factors in deciding whether to apply the fragmentation correction or to calculate a plot age that is a combination of the fragment-corrected date and the normal FT-corrected date: (a) whether the fragment-corrected dates are systematically younger than the corrected dates of unbroken grains, (b) whether there is geologic context to suspect earlier fragmentation, and (c) whether there is a date–size correlation of corrected dates of unbroken grains.
Despite the dispersion of raw dates due to fragmentation, it is possible to accurately correct for the effect of fragmentation based on basic measurements routinely recorded during the grain selection process. In compensating for the effects of alpha ejection in broken crystals, the FT correction should be calculated by explicitly taking into account the surface area of the broken face, rather than by assuming the unknown length of the original unbroken crystal. In individual cases, especially crystals with smaller widths or whose lengths are less than or around the same as their widths, the difference in apparent dates calculated with the two methods can be 12 % or greater.
We further applied both the previous and newly proposed protocols for the correction of broken crystals to a synthetic dataset. Even taking into account the effects of the diffusive loss of helium and breakage close to the tips of crystals, the proposed protocol more accurately and more precisely approximates the FT-corrected date of an unbroken crystal for a range of complex and simple thermal histories. For a crystal of 150 µm width, the old calculation leads to apparent dates that are on average 3 % older than the corrected dates of unbroken crystals, and, in extreme cases, up to 20 % (e.g., for drum-shaped fragments with no terminations that experienced gradual reheating).
The proposed adjustment allows more accurate comparison of data between samples of varying quality, which are common when a mix of different rock types is sampled. The greatest effect will be for samples where the majority of crystals are broken. Though this adjustment is minor in many cases, when applied to entire datasets, it significantly reduces one common source of error in calculations of individual apparent dates, and removes an easily correctable source of systematic bias towards older dates.
Kernel density plots were produced using DensityPlotter (https://doi.org/10.1016/j.chemgeo.2012.04.021, Vermeesch, 2012).
Individual corrected fragment dates can be found in the Supplement, and were calculated using methods discussed in the text and applied to the cited synthetic datasets.
The supplement related to this article is available online at: https://doi.org/10.5194/gchron-4-629-2022-supplement.
JJYH conceptualized the study and the new methodology, evaluated the precision and accuracy of the proposed correction, drafted the figures, and wrote the original draft; PWR advised on the conceptualization of the study and methodology, and reviewed and edited the manuscript.
The contact author has declared that neither of the authors has any competing interests.
Publisher's note: Copernicus Publications remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
We thank Richard Ketcham and an anonymous referee for their thorough and constructive reviews, and Stuart Thomson for the insightful discussions that led to this paper. John J. Y. He acknowledges the support of the H. Wesley and Maxine W. Peirce Scholarship and the ARCS Foundation Papadopoulos Fellowship. The analyses in this paper in part build upon the innovative work of Roderick Brown, whose careful consideration of the problem of crystal fragments in He dating, among many others, made lasting contributions to the thermochronology community.
This paper was edited by Cecile Gautheron and reviewed by Richard A. Ketcham and one anonymous referee.
Ault, A. K. and Flowers, R. M.: Is apatite U–Th zonation information necessary for accurate interpretation of apatite (U–Th)/He thermochronometry data?, Geochim. Cosmochim. Ac., 79, 60–78, https://doi.org/10.1016/j.gca.2011.11.037, 2012.
Beucher, R., Brown, R. W., Roper, S., Stuart, F., and Persano, C.: Natural age dispersion arising from the analysis of broken crystals: Part II. Practical application to apatite thermochronometry, Geochim. Cosmochim. Ac., 120, 395–416, https://doi.org/10.1016/j.gca.2013.05.042, 2013.
Brown, R. W., Beucher, R., Roper, S., Persano, C., Stuart, F., and Fitzgerald, P.: Natural age dispersion arising from the analysis of broken crystals. Part I: Theoretical basis and implications for the apatite thermochronometer, Geochim. Cosmochim. Ac., 122, 478–497, https://doi.org/10.1016/j.gca.2013.05.041, 2013.
Cooperdock, E. H. G., Ketcham, R. A., and Stockli, D. F.: Resolving the effects of 2-D versus 3-D grain measurements on apatite (U–Th) / He age data and reproducibility, Geochronology, 1, 17–41, https://doi.org/10.5194/gchron-1-17-2019, 2019.
Dana, E. S.: A Textbook on Mineralogy, John Wiley, New York, ISBN: 978-0471193050, 1963,
Farley, K. A.: Dating: Techniques, Calibrations, and Applications, Rev. Mineral. Geochem., 47, 819–844, https://doi.org/10.2138/rmg.2002.47.18, 2002.
Farley, K. A. and Stockli, D. F.: Dating of Phosphates, Rev. Mineral. Geochem., 15, 559–577, https://doi.org/10.2138/rmg.2002.48.15, 2002.
Farley, K. A., Wolf, R. A., and Silver, L. T.: The effects of long alpha-stopping distances on ages, Geochim. Cosmochim. Ac., 60, 4223–4229, https://doi.org/10.1016/S0016-7037(96)00193-7, 1996.
Farley, K. A., Shuster, D. L., and Ketcham, R. A.: U and Th zonation in apatite observed by laser ablation ICPMS, and implications for the system, Geochim. Cosmochim. Ac., 75, 4515–4530, https://doi.org/10.1016/j.gca.2011.05.020, 2011.
Fitzgerald, P. G., Baldwin, S. L., Webb, L. E., and O'Sullivan, P. B.: Interpretation of single grain ages from slowly cooled crustal terranes: A case study from the Transantarctic Mountains of southern Victoria Land, Chem. Geol., 225, 91–120, https://doi.org/10.1016/j.chemgeo.2005.09.001, 2006.
Flowers, R. M., Ketcham, R. A., Shuster, D. L., and Farley, K. A.: Apatite thermochronometry using a radiation damage accumulation and annealing model, Geochim. Cosmochim. Ac., 73, 2347–2365, https://doi.org/10.1016/j.gca.2009.01.015, 2009.
Flowers, R. M., Zeitler, P. K., Danišík, M., Reiners, P. W., Gautheron, C., Ketcham, R. A., Metcalf, J. R., Stockli, D. F., Enkelmann, E., and Brown, R. W.: chronology: Part 1. Data, uncertainty, and reporting, Geol. Soc. Am. Bull., Themed Issue: Reporting and Interpretation of Geochronologic Data, 1–33, https://doi.org/10.1130/B36266.1, 2022a.
Flowers, R. M., Ketcham, R. A., Enkelmann, E., Gautheron, C., Reiners, P. W., Metcalf, J. R., Danišík, M., Stockli, D. F., and Brown, R. W.: chronology: Part 2. Considerations for evaluating, integrating, and interpreting conventional individual aliquot data, Geol. Soc. Am. Bull., Themed Issue: Reporting and Interpretation of Geochronologic Data, 1–25, https://doi.org/10.1130/B36268.1, 2022b.
Gautheron, C., Tassan-Got, L., Ketcham, R. A., and Dobson, K. J.: Accounting for long alpha-particle stopping distances in (U-Th-Sm)/He geochronology: 3D modeling of diffusion, zoning, implantation, and abrasion, Geochim. Cosmochim. Ac., 96, 44–56, https://doi.org/10.1016/j.gca.2012.08.016, 2012.
He, J., Thomson, S. N., and Reiners, P. W.: Apatite thermochronometric data show rapid late Eocene incision in the central Transantarctic Mountains, AGU Fall Meeting Abstracts, vol. 2019, C53B-1340, https://ui.adsabs.harvard.edu/abs/2019AGUFM.C53B1340H/abstract (last access: 24 October 2022), 2019.
He, J., Thomson, S. N., Reiners, P. W., Hemming, S. R., and Licht, K. J.: Rapid erosion of the central Transantarctic Mountains at the Eocene-Oligocene transition: Evidence from skewed date distributions near Beardmore Glacier, Earth Planet. Sc. Lett., 567, 117009, https://doi.org/10.1016/j.epsl.2021.117009, 2021.
Herman, F., Braun, J., Senden, T. J., and Dunlap, W. J.: thermochronometry: Mapping 3D geometry using micro-X-ray tomography and solving the associated production-diffusion equation, Chem. Geol., 242, 126–136, https://doi.org/10.1016/j.chemgeo.2007.03.009, 2007.
Hourigan, J. K., Reiners, P. W., and Brandon, M. T.: U-Th zonation-dependent alpha-ejection in chronometry, Geochim. Cosmochim. Ac., 69, 3349–3365, https://doi.org/10.1016/j.gca.2005.01.024, 2005.
Ketcham, R. A., Gautheron, C., and Tassan-Got, L.: Accounting for long alpha-particle stopping distances in (U-Th-Sm)/He geochronology: Refinement of the baseline case, Geochim. Cosmochim. Ac., 75, 7779–7791, https://doi.org/10.1016/j.gca.2011.10.011, 2011.
Meesters, A. G. C. A. and Dunai, T. J.: Solving the production-diffusion equation for finite diffusion domains of various shapes: Part I. Implications for low-temperature thermochronology, Chem. Geol., 186, 333–344, 2002.
Murray, K. E., Orme, D. A., and Reiners, P. W.: Effects of U-Th-rich grain boundary phases on apatite helium ages, Chem. Geol., 390, 135–151, https://doi.org/10.1016/j.chemgeo.2014.09.023, 2014.
Palache, C., Clifford, F., and Berman, H.: The System of Mineralogy, John Wiley and Sons, OCLC no: 23114210, 1963.
Rahl, J., Reiners, P. W., Campbell, I. H., Nicolescu, S., and Allen., C. M.: Combined single-grain and dating of detrital zircons from the Navajo Sandstone, Utah, Geology, 31, 761–764, 2003.
Reiners, P. W. and Farley, K. A.: Influence of crystal size on apatite (U–Th)/He thermochronology: an example from the Bighorn Mountains, Wyoming, Earth Planet. Sc. Lett., 188, 413–420, https://doi.org/10.1016/S0012-821X(01)00341-7, 2001.
Reiners, P. W., Thomson, S. N., McPhillips, D., Donelick, R. A., and Roering, J. J.: Wildfire thermochronology and the fate and transport of apatite in hillslope and fluvial environments, J. Geophys. Res., 112, F04001, https://doi.org/10.1029/2007JF000759, 2007.
Reiners, P. W., Carlson, R. W., Renne, P. R., Cooper, K. M., Granger, D. E., McLean, N. M., and Schoene, B.: Geochronology and Thermochronology, Wiley, Oxford, UK, ISBN: 978-1-118-45578-4, 2018.
Spiegel, C., Kohn, B., Belton, D., Berner, Z., and Gleadow, A.: Apatite (U-Th-Sm)/He thermochronology of rapidly cooled samples: The effect of He implantation, Earth Planet. Sc. Lett., 285, 105–114, https://doi.org/10.1016/j.epsl.2009.05.045, 2009.
Thomson, S. N., Reiners, P. W., Hemming, S. R., and Gehrels, G. E.: The contribution of glacial erosion to shaping the hidden landscape of East Antarctica, Nat. Geosci., 6, 203–207, https://doi.org/10.1038/ngeo1722, 2013.
Thomson, S. N., Reiners, P. W., He, J., Hemming, S. R., and Licht, K.: New constraints on the pre-glacial and glacial uplift and incision history of the central Transantarctic Mountains using multiple low-temperature thermochronometers, AGU Fall Meeting Abstracts, Vol. 2019, C14B-04, https://ui.adsabs.harvard.edu/abs/2019AGUFM.C14B..04T/abstract (last access: 24 October 2022), 2019.
Vermeesch, P.: On the visualisation of detrital age distributions, Chem. Geol., 312–313, 190–194, https://doi.org/10.1016/j.chemgeo.2012.04.021, 2012.
Whipp, D. M., Kellett, D. A., Coutand, I., and Ketcham, R. A.: Short communication: Modeling competing effects of cooling rate, grain size, and radiation damage in low-temperature thermochronometers, Geochronology, 4, 143–152, https://doi.org/10.5194/gchron-4-143-2022, 2022.
Wolf, R. A., Farley, K. A., and Kass, D. M.: Modeling of the temperature sensitivity of the apatite thermochronometer, Chem. Geol., 148, 105–114, https://doi.org/10.1016/S0009-2541(98)00024-2, 1998.
Zeitler, P. K., Herczeg, A. L., McDougall, I., and Honda, M.: U-Th-He dating of apatite: A potential thermochronometer, Geochim. Cosmochim. Ac., 51, 2865–2868, https://doi.org/10.1016/0016-7037(87)90164-5, 1987.
Ziegler, J. F.: Helium: Stopping powers and ranges in all elemental matter, Vol. 4, Pergamon, New York, ISBN 10: 0080216064, 1977.
The requested paper has a corresponding corrigendum published. Please read the corrigendum first before downloading the article.
- Article
(3255 KB) - Full-text XML
- Corrigendum
-
Supplement
(894 KB) - BibTeX
- EndNote