Short communication: The Wasserstein distance as a dissimilarity metric for comparing detrital age spectra and other geological distributions

Distributional data such as detrital age populations or grain size distributions are common in the geological sciences. As analytical techniques become more sophisticated, increasingly large amounts of distributional data are being gathered. These advances require quantitative and objective methods, such as multidimensional scaling (MDS), to analyse large numbers of samples. Crucial to such methods is choosing a sensible measure of dissimilarity between samples. At present, the Kolmogorov–Smirnov (KS) statistic is the most widely used of these dissimilarity measures. However, the KS statistic has some limitations such as high sensitivity to differences between the modes of two distributions and insensitivity to their tails. Here, we propose the Wasserstein-2 distance (W₂) as an additional and alternative metric for use in geochronology. Whereas the KS distance is defined as the maximum vertical distance between two empirical cumulative distribution functions, the W₂ distance is a function of the horizontal distances (i.e. age differences) between observations. Using a variety of synthetic and real datasets, we explore scenarios where the W₂ may provide greater geological insight than the KS statistic. We find that in cases where absolute time differences are not relevant (e.g. mixing of known, discrete age peaks), the KS statistic can be more intuitive. However, in scenarios where absolute age differences are important (e.g. temporally and/or spatially evolving sources, thermochronology, and overcoming laboratory biases), W₂ is preferable. The W₂ distance has been added to the R package, IsoplotR, for immediate use in detrital geochronology and other applications. The W₂ distance can be generalized to multiple dimensions, which opens opportunities beyond distributional data.

1 Introduction

A distributional dataset is one where the information does not lie in individual observations but in the distribution of many observations associated with one sample. Such data are common in the geological sciences, for example, detrital mineral ages or grain size distributions. Zircon U–Pb ages, in igneous and detrital samples, are one particularly widely used class of distributional data, which are used inter alia to constrain sediment provenance, global magmatic processes, and the evolution of plate tectonics (e.g. Condie et al., 2009; Cawood et al., 2012; Reimink et al., 2021). Grain size distributions are another common form of geological distributional data. Analytical advances mean that increasingly large amounts of distributional data are being generated in the Earth sciences, meaning that qualitative comparison of samples is becoming infeasible, and objective dissimilarity metrics between samples must be used. Some measure of dissimilarity (or more specifically, distance) is also required for many widely used statistical methods such as clustering, ANOVA, and dimension reduction. Dissimilarity metrics in geochronology at present are most commonly used for dimension-reducing techniques such as multidimensional scaling (MDS) or principal component analysis (PCA). Such methods have become popular for analysing large numbers of detrital age spectra simultaneously (Vermeesch, 2013; Sharman et al., 2018; Vermeesch, 2018a). Fitting models (e.g. sediment source partitioning) using distributional data also requires a definition of dissimilarity for comparing observed and predicted distributions (e.g. Amidon et al., 2005; De Doncker et al., 2020).

For all uses, the choice of which dissimilarity metric to use is vital as different metrics result in different numerical results and thus different geological interpretations. In general, the most appropriate metric will depend on the data being analysed and the scientific question under investigation. The Kolmogorov–Smirnov (KS) distance, calculated as the maximum vertical distance between two empirical cumulative distribution functions (ECDFs), has emerged as a “canonical” distance metric between mineral age distributions (Berry et al., 2001; Vermeesch, 2018a). However, the KS distance has a number of drawbacks, chiefly that it is insensitive to variability in the tails of distributions since only the maximum vertical difference between ECDFs is important. A number of alternative dissimilarity measures have previously been proposed to address this issue, including established methods such as the Kuiper statistic and ad hoc dissimilarity measures such as the “likeness” and “cross-correlation” coefficients (Satkoski et al., 2013; Saylor et al., 2012). Unfortunately, these alternatives have drawbacks, including a propensity for the ad hoc dissimilarity measures to produce counterintuitive results when applied to extremely large and/or precise datasets (Vermeesch, 2018a).

In this paper, we present an alternative to the KS distance that does not suffer from some of these limitations: the Wasserstein distance (also known as the Earth mover's or Kantorovich–Rubinstein distance). To introduce the chief principle behind this measure, let us consider a simple toy example. Table 1 contains four samples (A through D), each of which contains exactly one single grain analysis.

Table 1 A toy, single grain per sample dataset.

As the KS distance is the vertical difference between ECDFs, it is insensitive to the absolute, “horizontal” age differences between individual observations. Thus, the KS distances between A and the other three samples are $\mathrm{KS}(\mathrm{A},\mathrm{B})=\mathrm{0}$, $\mathrm{KS}(\mathrm{A},\mathrm{C})=\mathrm{1}$ and $\mathrm{KS}(\mathrm{A},\mathrm{D})=\mathrm{1}$. Counter to our expectation, the KS distance cannot “see” the relative age difference between sample A and samples C and D. For the toy example, the Wasserstein distance simply corresponds to the horizontal distance between the four samples. Thus, $W(\mathrm{A},\mathrm{B})=\mathrm{0}$, $W(\mathrm{A},\mathrm{C})=\mathrm{1}$, and $W(\mathrm{A},\mathrm{D})=\mathrm{10}$, which is a more sensible result than that achieved with the KS distance.

In the following sections, we first introduce the Wasserstein distance in a more realistic setting and formally define it. Next, we discuss how it can be decomposed into intuitive terms that accord with how qualitatively, as geologists, we might compare distributions. We then proceed to compare the Wasserstein distance to the KS distance using a simple yet realistic synthetic example. Finally, we analyse a series of case studies, analysing real datasets using both the Wasserstein and KS distances. We thus evaluate the benefits and drawbacks of both metrics, identifying scenarios in which one metric may be preferred to the other. Whilst we focus primarily on detrital age distributions, we emphasize that much of the following discussion applies equally to any form of distributional data.

2 The Wasserstein distance

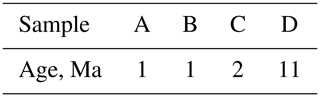
The Wasserstein distance is a distance metric between two probability measures from a branch of mathematics called “optimal transport”. Optimal transport is often intuited in terms of moving piles of sand from one location to another with no loss or gain of material (e.g. Villani, 2003). The problem that optimal transport solves is finding the way to transport the sand such that the least sand is moved the least distance. The Wasserstein distance is the cost associated with this most efficient transportation. The association with moving piles of sand is why the Wasserstein distance is often termed the Earth mover's distance. Figure 1a shows an example of how one univariate probability distribution, μ, based on a detrital age spectrum, is transformed into another, ν, according to the optimal transport plan. Elsewhere in the Earth sciences, the Wasserstein distance is increasingly used for solving non-linear geophysical inverse problems (e.g. Engquist and Froese, 2014; Métivier et al., 2016; Sambridge et al., 2022) and has been proposed as a tool for fitting hydrographs (Magyar and Sambridge, 2023). Full mathematical treatments of the Wasserstein distance and optimal transport are beyond the scope of this paper, but interested readers are referred to Villani (2003) or Peyré and Cuturi (2019). A geophysical perspective is given in Sambridge et al. (2022).

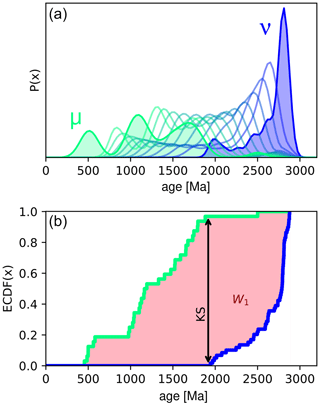
Figure 1 Intuition of the Wasserstein distance. (a) Green and blue filled polygons show two example kernel density estimates (KDEs) of mineral ages from two samples (based on data from Morton et al., 2008). The distributions are labelled μ and ν for consistency with Eq. (1). Semi-transparent coloured lines are probability distributions spaced equally in Wasserstein space between μ and ν (termed “barycentres”; Benamou et al., 2015). (b) Empirical cumulative distribution functions (ECDFs) of the detrital ages used to calculate the distributions shown in (a), same colours. The first Wasserstein (W₁) distance corresponds to the total area between the two ECDFs (shaded pink). The Kolmogorov–Smirnov (KS) distance is the maximum distance between the two ECDFs (black double-headed arrow).

2.1 Formal definition

We consider two univariate probability distributions, μ and ν, which have cumulative distribution functions (CDFs) M and N, respectively. The pth Wasserstein distance between μ and ν is given by

$$\begin{array}{}\text{(1)}& W_p(\mathit{\mu },\mathit{\nu })={\left(\underset{\mathrm{0}}{\overset{\mathrm{1}}{\int }}|M^{-\mathrm{1}}-N^{-\mathrm{1}}{|}^p\mathrm{d}t\right)}^{\mathrm{1}/p},\end{array}$$

where M⁻¹ indicates the inverse of the CDF M and $\mathrm{0}\le t\le \mathrm{1}$ (Villani, 2003). Note that this definition of W_p assumes that the cost function is given by $|x-y{|}^p$ (e.g. the Euclidean distance where p=2), which is the case for most distributional data in geology. In the further special case of p=1 (i.e. the first Wasserstein distance, W₁), Eq. (1) can be rewritten simply as

$$\begin{array}{}\text{(2)}& W_{\mathrm{1}}(\mathit{\mu },\mathit{\nu })=\underset{X}{\int }|M-N|\mathrm{d}x,\end{array}$$

which is the area between two CDFs (e.g. Fig. 1b). Recall that the KS distance between two distributions is the maximum distance between the two corresponding CDFs. Whilst the W₁ is easily visualized, we actually use the Wasserstein-2 distance (W₂) going forward since the squared distance (i.e. p=2) between observations is the standard distance metric in most statistical analyses (e.g. least squares regression). Additionally, the W₂ decomposes into readily interpretable terms, as discussed below.

We focus on these univariate instances as they apply to the most common geological distributional data including detrital age distributions and grain size distributions. However, we note that the Wasserstein distance is, in general, multivariate. As a result, some form of the Wasserstein distance could prove useful for analysing a number of other geological datasets such as the geochemical compositions of detrital minerals, or joint U–Pb and Lu–Hf isotope analysis (see Vermeesch et al., 2023). Statistics for comparing distributional data in multiple dimensions are increasingly needed (Sundell and Saylor, 2021).

Like the KS distance, the W₂ satisfies the triangle inequality, and as such, is a true metric. This property means that classical as well as metric and non-metric MDS can be used with a W₂-defined dissimilarity matrix. As W₂ is sensitive to absolute time differences, metric (or classical) MDS, which seeks to preserve absolute distances, may be preferable to non-metric MDS. For the rest of this paper, metric MDS is used.

2.2 Decomposition

A particularly useful property of the W₂ between two univariate distributions is that it can be decomposed in terms of the differences between the two distributions' location, spread, and shape. Irpino and Romano (2007) show that

$$\begin{array}{}\text{(3)}& W_{\mathrm{2}}^{\mathrm{2}}(\mathit{\mu },\mathit{\nu })=\stackrel{\mathrm{Location}}{\overbrace{(\stackrel{\mathrm{‾}}{\mathit{\mu }}-\stackrel{\mathrm{‾}}{\mathit{\nu }}{)}^{\mathrm{2}}}}+\stackrel{\mathrm{Spread}}{\overbrace{({\mathit{\sigma }}_{\mathit{\mu }}-{\mathit{\sigma }}_{\mathit{\nu }}{)}^{\mathrm{2}}}}+\stackrel{\mathrm{Shape}}{\overbrace{\mathrm{2}{\mathit{\sigma }}_{\mathit{\mu }}{\mathit{\sigma }}_{\mathit{\nu }}(\mathrm{1}-{\mathit{\rho }}^{\mathit{\mu }\mathit{\nu }})}},\end{array}$$

where $\stackrel{\mathrm{‾}}{\mathit{\mu }}$ is the mean of μ, σ_μ is the standard deviation of μ, and ρ^μν is the Pearson correlation coefficient between the quantiles of the distributions μ and ν. These three terms also accord with, qualitatively, how we as geologists might compare two distributions.

2.3 Discrete data

Most distributional data in the Earth sciences do not, in raw form, follow continuous probability distributions. Instead, samples may be discrete sets of observations, e.g. lists of individual mineral ages. The above formulations can be easily applied to such cases by describing the probability functions μ and ν as weighted sums of δ functions. For example, let us consider two samples x_m and x_n with p and q numbers of observations, respectively:

$$\begin{array}{}\text{(4)}& \mathit{\mu }=\sum _i^p{m}_i{\mathit{\delta }}_{x_m},\mathit{\nu }=\sum _i^q{n}_i{\mathit{\delta }}_{x_n},\end{array}$$

where m and n are weight vectors, such that $\sum m_i=\sum n_i=\mathrm{1}$. In most geological cases, these weights would be uniform, $m_i=\mathrm{1}/p$; $n_i=\mathrm{1}/q$, giving each observation within a sample equal weight. In this scenario, M and N are the familiar empirical cumulative distribution functions (ECDFs), given as a series of step functions (e.g. Fig. 1b).

2.4 A synthetic example

To demonstrate the intuition of the W₂, we explore a simple synthetic example. We consider two probability density functions of mineral ages: a bimodal distribution and a unimodal distribution, both constructed from Gaussians with the same scale (Fig. 2a). We fix the bimodal distribution at 1000 Ma but translate the unimodal distribution along the time axis. For each translated distribution, we calculate both the KS distance and W₂. Figure 2b displays the behaviour of both distances under this scenario. The KS distance shows an unexpectedly complex response containing a series of steps, as the peaks of the distributions align and misalign. At around ±400 Ma, once the distributions stop overlapping, the KS distance plateaus at its maximum value of 1. By contrast, the W₂ increases monotonically with increasing distance. Away from the origin, the W₂ approximates a linear function of the amount of translation, as is predicted from Eq. (3). At the origin, the non-zero value of the W₂ is the cost of turning the unimodal distribution into the bimodal distribution without translation.

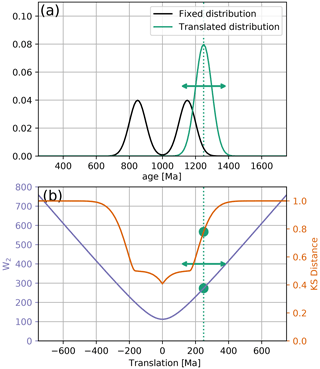
Figure 2 Comparing the Wasserstein distance to the Kolmogorov–Smirnov distance. (a) Two synthetic probability density functions, modelled on the U–Pb age spectra. The black bimodal distribution is fixed at 1000 Ma, and the green unimodal distribution is translated along the time axis. (b) For each translated distribution, we calculate the KS distance (red line) and the W₂ (blue line). The dashed green line and circles indicate values associated with the location of the green distribution shown in (a).

We argue that the behaviour of the W₂ is more geologically intuitive than the KS distance under this scenario. It is useful geological information if two distributions differ in their means by 400, 500, or 1000 Ma, but if the distributions do not overlap, the KS distance is insensitive to this. The Wasserstein distance is, by contrast, sensitive to the absolute offset between non-overlapping distributions. Additionally, the stepped response of the KS distance under translation is undesirable. Under the simple operation of translating a unimodal distribution, we would expect our dissimilarity to increase at a constant, or at least predictable (e.g. quadratic), rate. The change of the KS distance with translation is, counterintuitively, non-linear. By contrast, the W₂ increases linearly with respect to translation.

We reiterate that at a translation of 0 Ma, the W₂ (and the KS distance) is still non-zero, reflecting the fact that even when the average ages are aligned, the shapes of the unimodal and bimodal distributions do not match. This illustrates the tendency of the W₂ in geochronological data to prioritize aligning the average ages of distributions before considering matching individual peaks. Such behaviour contrasts with approaches that seek to only match probability peaks neglecting any information of absolute ages (e.g. Saylor and Sundell, 2016).

3 Discussion

As stated above, the most appropriate dissimilarity metric to use will depend on the scientific question being answered. In general, the Wasserstein distance is most appropriate when absolute differences along the time axis (or more generally, the x axis) provide useful information to solving the geologic problem. The KS distance, however, is more appropriate when the size of the time differences between peaks is not relevant. Both the KS distance and the W₂ are calculated in terms of differences between ECDFs. Due to these similarities in construction, in many cases the results from using the KS distance and W₂ are, encouragingly, similar. One exception is whether ages are log-transformed prior to analysis. Because the KS distance considers only the order of the ages, it will be the same whether a log transform is used or not. The W₂, however, will be different, and it will consider relative not absolute age differences. Such an example is discussed below (Fig. 5).

Here, we discuss a variety of realistic scenarios where the KS and W₂ may result in different interpretations. In each, we evaluate the advantages and disadvantages of using the W₂ or KS. These case studies can be used to determine which metric is most appropriate for a particular scenario.

3.1 Discriminating contributions from discrete endmembers

We first consider a scenario where the samples are assumed to be mixtures, in differing proportions, of some known or unknown fixed endmembers. This situation is one where absolute distance along the time axis is not relevant, as the nature of the endmembers is not sought, simply their relative contributions to a set of mixtures. Instead, it is the vertical differences in the probability at a given age that are relevant. The KS distance, which is sensitive to such vertical differences in age distributions, is better suited for this than the W₂. Indeed, in such a scenario, the W₂ can result in some counterintuitive behaviour.

Figure 3 Mixing of discrete endmembers. (a) Three theoretical, unimodal source age distributions with peaks at 10, 20, and 100 Ma, and two mixture samples. Sample 1 is an equal mixture of X and Y and Sample 2 a mixture of Y and Z. (b) Metric MDS map of the three sources and the mixtures using the W₂ (stress = 0.05). (c) Same as (b) for KS distance (stress = 0.05). This is a scenario where KS distance may be preferable to W₂.

For example, let us consider three unimodal potential sediment sources, as shown in Fig. 3a. We now consider two mixture samples. The first is an equal mixture of X and Y, and the second is an equal mixture of Y and Z (bottom two plots, Fig. 3a). Geologically, we would expect these samples to be about half as similar to the two source endmembers. However, a W₂ MDS map identifies these samples as being removed from their two endmembers (Fig. 3b). Additionally, because of the absolute time difference between Source Z and the other sources, Sample 2 is treated as a considerable outlier. The KS distance performs better here, placing the mixtures approximately halfway between the expected endmembers. However, in such a well-defined mixing scenario as this, methods such as endmember mixture modelling may be more appropriate than statistical dimension reduction (e.g. Weltje, 1997; Sharman and Johnstone, 2017; Dietze and Dietze, 2019).

3.2 Temporally varying source age distributions

In contrast, scenarios where the shape of sediment source age distributions evolves in space and time are well suited to using the W₂. This is because the W₂ considers all parts of a distribution, whereas the KS distance only compares one point, the location of maximum ECDF separation. For example, Fig. 4 displays detrital zircon age distributions gathered by DeGraaff-Surpless et al. (2002) from sediments from a section (Cache Creek) across the Great Valley Group in California, USA. The age populations are shown as kernel density estimates (KDEs) and histograms, in stratigraphic order, in Fig. 4a. The uppermost samples show an increasingly broader distribution than the lower four unimodal samples. DeGraaff-Surpless et al. (2002) attribute this trend, inter alia, to expanding sediment source areas.

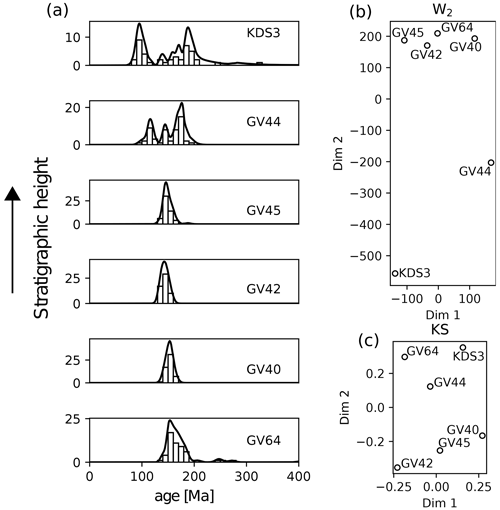
Figure 4 Temporally evolving source distributions. (a) KDEs and histograms for zircon age distributions for samples from the Cache Creek section across the Great Valley Group, arranged in stratigraphic order (DeGraaff-Surpless et al., 2002). (b) MDS map using the W₂ (stress = 0.28) for data shown in (a). (c) Same as (b) using KS distance (stress = 0.18). In this scenario, the results from the W₂ are preferable.

Figure 4b–c displays MDS maps calculated using the W₂ and KS distance, respectively. The W₂ map clearly identifies the stratigraphic order of the samples by the changing distribution shape. Additionally, it clusters the four unimodal samples together. By contrast, the KS map does not identify the stratigraphic trend, locating the lowermost stratigraphic sample GV64 with the uppermost samples KDS3 and GV44. We conclude then that the W₂ has better captured the geological information in this scenario.

3.3 Thermochronology

In thermochronology, age distributions shift along the time axis according to thermal signals (e.g. exhumation). In many thermochronological studies, we may seek to characterize how such a signal evolves in space and time. For this question, absolute distance along the time axis is useful information and so the W₂ may be more effective than the KS distance. For example, Wobus et al. (2003) use ${}^{\mathrm{40}}\mathrm{Ar}{/}^{\mathrm{39}}\mathrm{Ar}$ detrital mica thermochronometry to explore spatially varying exhumation along a spatial transect in the Himalaya. The KDEs of the samples are shown in Fig. 5a, arranged south to north. The southern samples (WBS1, WBS2, WBS3, WBS8) show old exhumation signals, but a dramatic shift to younger ages is observed north of a distinct physiographic transition. The MDS maps of these samples are shown using the KS distance and the W₂ in Fig. 5b–c, respectively. As there is limited overlap between the samples, the KS distance struggles to capture the north–south progression in exhumation age. Whilst the physiographic division is found, it weights it equally to variation within one cluster. By contrast, the W₂ map correctly identifies the simple temporal and geographical trend of the samples from south to north.

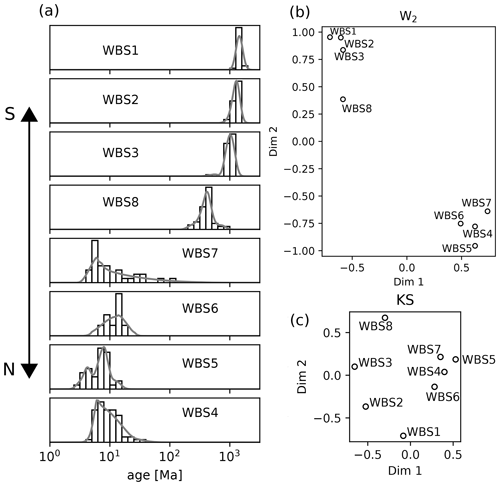
Figure 5 Analysing thermochronological data using W₂ and KS distances. (a) KDEs for a detrital mica ${}^{\mathrm{40}}\mathrm{Ar}{/}^{\mathrm{39}}\mathrm{Ar}$ dataset of Wobus et al. (2003) arranged from south to north across a physiographic transition of the central Himalaya in Nepal. Note the logarithmic scale. (b) The MDS configuration using the W₂, following a log transform (stress = 0.02). (c) MDS map using the KS statistic (stress = 0.18). In this example, the W₂ performs better than the KS distance at identifying the geographic trend.

3.4 Combining data from multiple laboratories

A final scenario where the W₂ could be preferable is when comparing samples from different laboratories which are affected by interlaboratory bias. Košler et al. (2013) provided 10 different laboratories with identical synthetic zircon samples with a known age distribution. Different instruments introduced small differences in the ages of each peak. For example, in Fig. 6, we display the results from Lab 1 (red) and Lab 4 (pink) as KDEs. The expected peak at ∼1200 Ma (dashed line) is offset between the two samples. As it is the maximum distance between two ECDFs, the KS distance is very sensitive to minor offsets in sharply defined peaks. In this case, the KS distance between these theoretically identical samples is large at 0.348, which is over one third of the maximum possible distance between samples. Indeed, the KS distance considers a synthetic, purposefully misaligned series of peaks (black KDE) to be more similar to the Lab 4 results than the results from Lab 1. The W₂ does not suffer from this oversensitivity to minorly offset peaks and correctly identifies the samples from Lab 1 and Lab 4 as being much more similar than the random synthetic distribution.

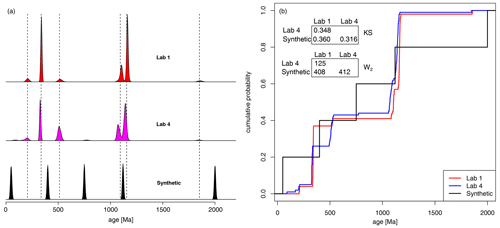
Figure 6 Comparing samples from an interlaboratory calibration study. KDEs (a) and ECDFs (b) of two samples from the interlaboratory comparison study of Košler et al. (2013), plus a purposefully misaligned synthetic sample. Dashed lines mark the true ages of the detrital mixture. According to the KS statistic, the age distribution produced by Lab 4 is more similar to the synthetic distribution than it is to the distribution produced by Lab 1, despite the absence of any shared age components. The W₂ correctly deems the distribution produced by Lab 4 to be closer to that of Lab 1 than to the synthetic mixture.

4 Implementation

We provide the example code (https://doi.org/10.5281/zenodo.7937484) in both Python and R that demonstrates how to calculate the W₂ between two univariate distributions (U–Pb zircon ages). For these examples, we make use of the POT and transport packages in Python and R, respectively, which implement solutions to Eq. (1) (Flamary et al., 2021; Schuhmacher et al., 2022).

IsoplotR

Additionally, the W₂ has been added to the IsoplotR package in R, which calculates dissimilarity matrices and MDS maps (Vermeesch, 2018b). This software can be accessed using a (online) graphical user interface at https://isoplotr.es.ucl.ac.uk/ (last access: 15 May 2023). Alternatively, the function can also be accessed from the R command line. The following snippet uses the W₂ to calculate an MDS map for the dataset from Wobus et al. (2003) discussed in the paper (Fig. 5). The data required are also available at the above repository. Note that the MDS map produced may show slight differences to those in the paper due to the dependence of metric MDS on a random state variable. This variability can introduce reflections and/or rotations of the data, but the underlying structure is unchanged.

# load the package:
library(IsoplotR)

# Load in the data
DZ <- read.data("wobus.csv",
      method="detritals")

# example 1. calculate the W2 distance
  matrix for the dataset:
d <- diss(DZ,method="W2")

# example 2. apply MDS to the dataset:
mds(DZ,method="W2")

5 Conclusions

The second Wasserstein distance, W₂, is an effective metric for comparing distributional data in the geological sciences such as detrital age spectra or grain size. Unlike the KS distance, the W₂ can be extended to further dimensions. The W₂ is a function of the horizontal distances between observations, in contrast to the KS distance, which corresponds to vertical differences between ECDFs. Using a variety of case studies, we explore scenarios where the W₂ may or may not be preferable to the KS distance. In scenarios where discrete, known age peaks are mixed, the KS distance may be preferable. However, in other scenarios where absolute differences along the time axis are useful information, the W₂ is preferable. Example scenarios include spatially and/or temporally evolving source distributions, thermochronological data, and combining detrital samples from different laboratories. The Wasserstein distance has been added to the IsoplotR software, and example scripts are provided in Python and R.