Diffusion kinetics of ³He in pyroxene and plagioclase and applications to cosmogenic exposure dating and paleothermometry in mafic rocks

In this study, we investigate the diffusivity of cosmogenic ³He in a variety of plagioclase and pyroxene compositions, and its application to paleothermometry and exposure dating in these minerals, through stepwise degassing experiments. While cosmogenic ³He has been utilized for exposure dating in pyroxene for decades due to its retentivity, plagioclase, often found along with pyroxene in mafic rocks, is generally less retentive of cosmogenic noble gas. However, the diffusivity of ³He in either plagioclase or pyroxene has not yet been measured quantitatively. A challenge in measuring diffusion kinetics by step-degassing experiments in poorly retentive minerals is the fact that significant amounts of He can be lost prior to the experiment. To address this issue, we apply a forward “multiple diffusion domain” (MDD) inversion model that includes model predictions of initial gas loss during irradiation and storage of the samples to account for this observation and add constraints to the diffusion parameters. We find that ³He diffusivity in plagioclase appears to be highly variable. This variability can be explained by the MDD inversion models' inability to constrain the diffusion parameters when significant gas has been lost during irradiation and/or prolonged storage prior to experiment analysis, resulting in an overestimation of ³He retentivity. Plagioclase samples that were kept frozen after irradiation, to limit this initial gas loss, yielded the most reliable estimate of diffusion kinetics. We find that ³He in plagioclase is diffusively lost at Earth's surface temperatures on a timescale of 100 years and is therefore unsuitable for surface temperature paleothermometry. On the contrary, we find cosmogenic ³He in pyroxene to be retentive at Earth's surface temperatures on a 1-million-year timescale.

1 Introduction

We measured ³He diffusivity in various plagioclase and pyroxene grains to determine their diffusion kinetic parameters and potential usefulness for paleothermometry and exposure dating. Cosmogenic ³He has been used for cosmogenic nuclide dating for decades and is produced in mineral matter near Earth's surface by spallation and muon production by cosmic rays. The utilization of ³He in pyroxene for exposure dating is well established (e.g., Craig and Poreda, 1986; Bruno et al., 1997; Ackert et al., 1999; Schäfer et al., 1999; Balter-Kennedy et al., 2020; Tremblay et al., 2014b), on the assumption that ³He is well retained at Earth's surface temperatures. While these studies do not quantify the diffusion kinetics of ³He, they do indeed confirm that ³He is well retained, as measured ³He concentrations in pyroxene are consistent with exposure ages determined from other geological evidence. Plagioclase is often found along with pyroxene in mafic rocks but is less retentive of cosmogenic noble gases (Megrue, 1966; Cerling, 1990; Bruno et al., 1997; Gourbet et al., 2012; Cassata and Renne, 2013; Tremblay et al., 2017). This limits the application of plagioclase for cosmogenic nuclide exposure dating but provides potential usefulness for surface temperature thermochronometry, which relies on temperature-dependent diffusion of noble gases in mineral matter (Tremblay et al., 2017). However, the diffusion kinetics of cosmogenic ³He in both pyroxene and plagioclase have not yet been determined.

Using predictive models of cosmogenic noble gas production and diffusive loss through time and temperature in mineral matter, a quantitative constraint on the thermal history of an exposed rock surface can be inferred from a surface exposure age derived from, e.g., cosmogenic nuclide dating (Tremblay et al., 2014b, a, 2017; Gribenski et al., 2022). In other words, even if the loss of a diffusively mobile nuclide precludes its use to determine the exposure age, it might allow one to determine the surface temperature. Currently, paleothermometry relies on the open-system behavior of cosmogenic ³He in quartz at Earth surface temperatures (Brook et al., 1993; Shuster and Farley, 2005). Since He is also produced by the decay of uranium and thorium, its diffusivity in mineral matter has been studied extensively as chronometers in terrestrial and extraterrestrial materials (summarized in Baxter, 2010). While the diffusion kinetics of ³He and ⁴He have been determined in various minerals, we are not aware of any measurements of He diffusion in plagioclase. The only existing constraint on He diffusion in pyroxene was reported by Lippolt and Weigel (1988), who determined ⁴He in pyroxene to be generally retentive on a geological timescale at low temperatures (<50 °C).

The diffusivity of noble gases can be measured from a stepwise degassing experiment of a single mineral grain in which the grain is repeatedly heated at steadily increasing temperatures until the included gas is exhausted. In simple cases, diffusion coefficients derived from the fractional release of gas in each step form a linear array in an Arrhenius plot, in which the slope of the array is proportional to the material activation energy (e.g., Gourbet et al., 2012). When some data diverge from this linear array, diffusion kinetics are often estimated simply by fitting a straight line to the linear portion of the data set and disregarding any divergent data (e.g., Shuster and Farley, 2005; Gourbet et al., 2012; Cassata and Renne, 2013). Because thermochronological studies rely on applying the extrapolation of laboratory-determined diffusion properties to geological settings, the magnitude of the diffusion parameters, such as activation energy (E_a) and pre-exponential factor (D₀), is particularly significant for determining temperature-dependent gas release. However, since a subset of the step-heating experimental data is used for determining these parameters, the excluded data may hold important information on diffusion kinetics that is not accounted for.

Previous diffusion experiments of ²¹Ne, ³⁷Ar, and ³⁹Ar in plagioclase and pyroxene are known to show complex diffusion behavior, expressed as diffusion coefficients that form multiple linear or curvilinear arrays on Arrhenius plots (Gourbet et al., 2012; Cassata and Renne, 2013; Tremblay et al., 2017), which has commonly been explained by so-called “multiple diffusion domain” (MDD) models to describe the overall diffusion kinetics (Lovera et al., 1989, 1997). In the MDD model, the nonlinearity is explained by the systematic exhaustion of sub-grain domains that are usually envisioned to consist of the same material with the same activation energy but with different effective sizes. Since its development, the MDD model has been widely used in thermochronology (e.g., Reiners et al., 2005), including surface temperature thermochronology from cosmogenic ³He diffusion in quartz (Gribenski et al., 2022).

Originally, the MDD model was developed to determine the diffusion kinetics for minerals with high closure temperatures compared to Earth's surface temperatures. Thus, zero degassing would occur during storage, and gas would only be released during experimental heating steps. However, applying any method for determining diffusion kinetics (MDD or single Arrhenius domain) to minerals that have closure temperatures near room temperature requires accounting for the fact that the sample loses gas at ambient conditions. Any loss of gas before a step-heating experiment results in an initially heterogeneous distribution of the gas concentration, which in turn yields an anomalously elevated slope at low temperatures on Arrhenius arrays calculated assuming an initially homogeneous distribution (Shuster and Farley, 2005; Tremblay et al., 2014b, 2017).

Previous studies of diffusion kinetics by step-degassing in non-retentive minerals (e.g., ³He in quartz) have found that the first few initial heating steps <100 °C often lie below the linear array in the Arrhenius plot and exhibit increasing apparent diffusivity (Tremblay et al., 2014b). This has been explained by the diffusive loss of gas either during or after proton irradiation (Shuster and Farley, 2005). As a result, the first few heating steps are often neglected from the regression line used to determine the activation energy (e.g., Gourbet et al., 2012; Cassata and Renne, 2013), or two different diffusion kinetics are modeled separately for a higher and lower temperature domain (Tremblay et al., 2014b).

The goal of this study is to determine the diffusion kinetics of cosmogenic ³He in plagioclase and pyroxene and to evaluate the use of these mineral nuclide pairs in paleothermometry and exposure dating. We do so by measuring the ³He diffusivity through stepwise degassing experiments on plagioclase and pyroxene fragments from the Ferrar Dolerite in Antarctica and on grains from a variety of feldspar and pyroxene end-member compositions. We then apply an optimization approach similar to that of Gorin et al. (2024) for determining the diffusion kinetics by predicting the gas releases using an MDD forward inversion model and comparing the modeled results with the measurements. Although estimation of diffusion kinetic parameters from a step-degassing experiment is usually routine, we find that ³He in plagioclase is diffusive at room temperatures and violates the usual assumption that an initial inventory of ³He is fully retained until the beginning of the experiment. Thus, it is necessary to account for the loss of ³He prior to experimental analysis. We therefore include model predictions of gas loss during and after irradiation. We find that accounting for such diffusive loss has a significant effect on both (i) the diffusion kinetics inferred from model inversions and (ii) inferred geologic conditions that attend cosmogenic production.

2 Method

We conducted stepwise diffusion experiments on single feldspar and pyroxene grains from various rock samples. For a diffusive mineral, by which we mean minerals that incompletely retain helium at Earth's surface temperature, natural cosmic-ray-produced ³He in a sample grain will have a nonuniform distribution and be unsuitable for step-heating experiments used for determining diffusion kinetics. Therefore, all sample grains were either proton- or neutron-irradiated. Proton irradiation of the grains results in the production and homogeneous distribution of ³He through nuclear reactions similar to those produced from naturally induced cosmic rays but with a concentration 1 order of magnitude higher than naturally produced cosmogenic ³He. Neutron irradiation is intended for the production of ³⁹Ar from K for the purposes of ${}^{\mathrm{40}}\mathrm{Ar}{/}^{\mathrm{39}}\mathrm{Ar}$ dating, and the neutron-irradiated samples described here were irradiated for that purpose. However, ³He is also produced as a byproduct, so these samples can also be used for ³He diffusion experiments. In both cases, the production of ³He at levels well above naturally occurring concentrations allows more precise and detailed stepwise degassing experiments on single grains (Shuster et al., 2004; Shuster and Farley, 2005; Tremblay et al., 2014b).

2.1 Samples and irradiation

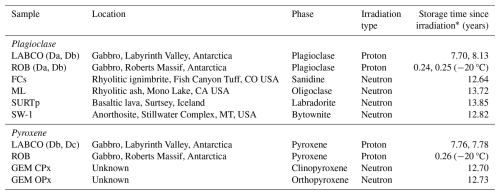
In this study, we analyzed feldspar and pyroxene grains from two distinctly different sample groups (Table 1). One group of samples consists of various feldspar and pyroxene grains from well-studied localities, whereas the other group consists of plagioclase and pyroxene grains from the Ferrar Dolerite, an intrusive gabbroic rock found in the Transantarctic Mountains (TAM), Antarctica. The Ferrar consists predominantly of subequal parts of plagioclase and pyroxene (Harvey, 2001; Elliot and Fleming, 2021), and its high resistance to weathering makes it one of the most dominant rocks exposed at the surface in Antarctica. Therefore, it is commonly used for exposure-dating applications. For this study, we obtained grains from two separate Ferrar Dolerite samples. The LABCO sample is a core sample from the Labyrinth in the McMurdo Dry Valleys, collected in 2009 as part of the CRONUS-Earth project and described in Balter-Kennedy et al. (2023). The ROB samples are from glacial moraine boulders collected at Roberts Massif in the central TAM for ³He exposure dating (Balter-Kennedy et al., 2020).

Table 1 Sample description.

^∗ Assumed to be at room temperature (∼21 °C), except for ROB (Da, Db).

Each rock sample was crushed, and individual crystal fragments of plagioclase and pyroxene devoid of any obvious microfractures under a microscope were handpicked. Numerous grains from a given sample were packed in aluminum foil, put into small (9 mm×3 mm) HDPE capsules, stacked into quartz tubes, and proton-irradiated for ∼8 h at temperatures of <45 °C at the Harvard Cyclotron Facility following an established methodology (Shuster et al., 2004). The LABCO plagioclase and pyroxene samples were proton-irradiated in December 2014 and have since been stored at room temperature (∼21 °C). The ROB samples were proton-irradiated in March 2024, cooled to −25 °C after irradiation for 1 month, and kept frozen at −20 °C until analysis (∼2 months) at the Berkeley Geochronology Center (BGC), resulting in a total storage time of approximately 3 months at freezing temperature.

The group of samples, consisting of various feldspar and pyroxene grains having known composition (Table 1), has been the subject of extensive mineralogical research for decades and used in previous diffusion studies for determining the diffusion kinetics of Ar (Cassata et al., 2011; Cassata and Renne, 2013) and Ne (Gourbet et al., 2012; Tremblay et al., 2017). The feldspar samples were neutron-irradiated by Cassata and Renne (2013; see reference for more details), and the pyroxene samples were neutron-irradiated by Cassata et al. (2011; see reference for more details). The temperature during neutron irradiation is unknown but has been estimated to reach at least 150 °C and perhaps as high as 200 °C for a duration of either 50 or 100 h (Personal communication with the Cadmium-Lined In-Core Irradiation Tube (CLICIT) facility at Oregon State University, where samples were irradiated). Since irradiation, the samples have been stored at room temperature (∼21 °C) at BGC for variable durations (Table 1).

2.2 Step-heating experiment

Single grains used for step-heating experiments were selected under a microscope after irradiation. To eliminate any complications arising from variation in grain size, shape, and other properties, the grains were selected by the following criteria: (i) rounded shape, (ii) single crystal, (iii) similar size, and (iv) void of any visually apparent fractures and impurities. Photos from each selected grain were obtained, and its dimensions were recorded before and after the experiment (Figs. S1 and S2 in the Supplement).

At BGC, irradiated single-sample grains were loaded into small (∼5 mm) Pt–Ir alloy or Ta packages connected to a type-K thermocouple and attached to the “Ohio” noble gas mass spectrometer extraction line under high vacuum ($<{\mathrm{10}}^{-\mathrm{8}}$ Torr). The package containing the sample was heated with a 30 W diode laser focused on the package to obtain uniform heating. The laser and thermocouple were connected in a control loop using a Watlow PID controller that achieves a typical accuracy of <3 °C. The exact duration and temperature of the heating were determined by the assigned heating schedule (Tables S1 and S2 in the Supplement) and adjusted for the type of mineral being analyzed. None of the diffusion experiments resulted in melting or visual changes for either plagioclase or pyroxene grains.

All diffusion experiments included an initial heating step of 25 °C for 30–60 min, depending on mineral composition, followed by an increasing heating schedule that consists of a few repeating temperature steps where heating duration is increased and at least one retrograde at higher temperatures. While all steps are sensitive to the distribution of domain sizes, retrograde temperature cycling emphasizes their presence and is useful for constraining the activation energy (Lovera et al., 1989; Mcdougall and Harrison, 1999; Shuster and Farley, 2005).

The ³He measurement method follows that described in Tremblay et al. (2014b). Throughout the heating experiment, we measured 5–8 sample chamber blanks as a 30–60 min “heating” step at 25 °C. The initial heating step at this temperature commonly yielded significant amounts of ³He and was not considered a blank. A linear fitting of the sample chamber blanks was then subtracted from the raw signal in other heating steps. The magnitude of the blank varied between each experiment but averaged 10⁴ atoms of ³He. For heating steps where the gas release was insignificant from the blank level, the measured value was set to zero and included in the data set. The measured fractional gas release and the duration during each heating step were then used to calculate diffusion coefficients using the equations for spherical geometry derived by Ginster and Reiners (2018).

2.3 Forward MDD model

We fit a forward multiple diffusion domain (MDD) model to the step-degassing data to determine the diffusion kinetics for the various mineral grains. One of the main assumptions for the forward MDD model is that the same activation energy applies to all sub-grain domains and that each domain can exhibit varying diffusive length scales (e.g., different radii). The diffusion domain, n, in a grain with multiple diffusion domains can be described by (i) the activation energy, E_a (kJ mol⁻¹), which applies to all domains; (ii) the pre-exponential factor, $D_{\mathrm{0}}/a_n^{\mathrm{2}}$ (s⁻¹); and (iii) the proportion of the total gas contained in the domain. The fractional loss is calculated using the equations in Fechtig and Kalbitzer (1966, Eq. 4a–c) for each domain and scaled by the proportion of gas contained in the domain, such that the total cumulative fractional release is the sum of all releases within each domain.

Given a step-heating experiment, the forward MDD model then predicts the fractional gas release and calculates the apparent diffusion constant, $D/a^{\mathrm{2}}$ (s⁻¹) (Fechtig and Kalbitzer, 1966, Eq. 5a–c), during each heating step for n number of domains. This allows a direct comparison of the measured and predicted fractional release between all data points for a given diffusion experiment. When a single domain (n=1) is assigned to the forward MDD model, this converts to a simple Arrhenius linearity with 3 free parameters. For all other (n>1) domains, this will convert to a nonlinear Arrhenius behavior, with 2+2n free parameters in the MDD model.

2.3.1 Diffusion loss during irradiation and storage

Since these samples have experienced a long period of storage time between irradiation and analysis (Table 1), it is expected that non-retentive samples have lost gas in the outer grain boundary due to years of storage, even at room temperature (∼21 °C). Therefore, in the forward MDD model, we account for this initial gas loss prior to the step-heating experiment (referred to as initial loss). Within the forward MDD model, the initial irradiation and storage loss are temporally added as two separate heating steps to be included in the calculation of cumulative fractional release, such that the predicted fractional release from the first experimental heating steps reflects such initial loss. Once the predicted cumulative fractional release is determined, the two additional heating steps are removed, and the fractional release from each of the experimentally heating steps is re-scaled to sum 1 for direct comparison to the measured fractional gas release data points. When included, the two steps increase the degree of freedom in the forward MDD optimization model.

Gas loss during storage (we refer to this as storage loss) occurs between the irradiation and time of the diffusion experiment and is simply dependent on the diffusivity of gas within the mineral, duration, and temperature of the storage. Gas loss during irradiation (we refer to this as irradiation loss) is assumed to occur for diffusive samples as the temperature reaches up to 45 °C for 8 h during proton irradiation (Shuster et al., 2004). However, the exact temperature throughout the irradiation is not well known. For the samples that have been proton-irradiated, we include a modeled initial heating of an estimated 40 °C for 8 h in the forward MDD model. While we acknowledge that there is simultaneous production and diffusion of ³He during the irradiation, we only account for diffusion loss (see Discussion for more details), resulting in a maximum estimated gas loss. The true build-up and amount of gas present after irradiation lies between the two modeled end-members, (1) including diffusion loss only, during both irradiation and diffusion, and (2) not including any production or gas loss at all, which assumes that all the gas that is produced during irradiation is present at the start of the experimental analysis. The overall effect of simultaneous production and diffusion during irradiation on the total amount of ³He is insignificant unless the sample is diffusive at room temperature. However, in such a case, any storage (e.g., 1 month) of the sample at room temperature prior to step-heating analysis would suppress any measurable gas loss signal arising from the irradiation. The group of samples with known feldspar and pyroxene compositions was all neutron-irradiated for either 50 or 100 h (Cassata et al., 2011; Cassata and Renne, 2013), in which temperatures could reach up to 200 °C. Since all samples contain measurable He, it is indicative that, for a diffusive mineral, simultaneous production and gas loss do result in a measurable amount of ³He. As the exact temperature of neutron irradiation is unknown, we do not account for any irradiation loss when optimizing for the diffusion kinetics but instead only account for storage at room temperature (see Sect. 4.2.1 for more details). We acknowledge that, for neutron irradiation, (i) significantly higher temperatures are reached during irradiation than during proton irradiation, (ii) the production reaction of ³He is not well understood, and (iii) zoning in plagioclase may cause initial heterogeneous ³He distribution. Consequently, for a diffusive mineral, this results in an initial non-homogeneous distribution of ³He in the grain during irradiation. While this is not ideal, and it is clear that the high temperatures reached during irradiation make neutron irradiation a poor choice for measuring diffusion kinetics of poorly retentive minerals, we use the approach here because it allows us to take advantage of samples that were already irradiated for other purposes and to explore the diffusion kinetics in a variety of feldspar and pyroxene compositions.

In Fig. 1, we show the effect of a non-homogeneous gas distribution from proton irradiation, followed by storage loss modeled for a diffusive mineral, by applying arbitrary MDD diffusion kinetics for three domains to a simple increasing heating schedule with a high-temperature retrograde. Any gas loss prior to the diffusion experiment results in an apparent diffusivity that is lower than expected and increases for repeated temperature heating steps <250 °C. Accounting for irradiation loss of 40 °C for 8 h results in a gas loss of 0.51 % prior to the experimental analysis (Fig. 1a). The same sample would lose 6.26 % and 18.64 % of its gas during storage only at room temperature (21 °C) for 1 and 10 years, respectively (Fig. 1b). An interesting aspect of this effect is the observed change in apparent activation energy for low-temperature heating steps when determined from a linear regression. The magnitude of bias in apparent activation energy then depends on the number of initial data points excluded from the regression. As it is not clear how to choose these points in an unbiased way, this raises a significant disadvantage in the conventional linear regression approach. Our approach instead aims to fit all data, thus eliminating the need for potentially arbitrary data selection.

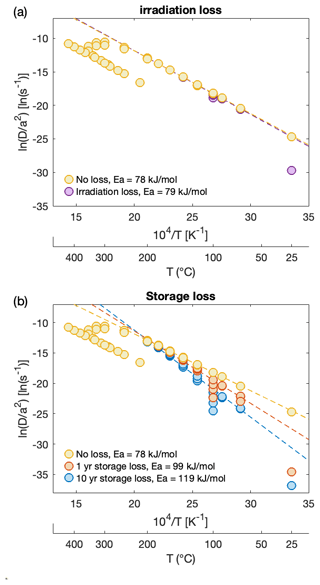
Figure 1 Calculated apparent diffusivities for (a) proton irradiation and (b) storage at room temperature (21 °C) for a diffusive mineral. All scenarios use an activation energy of 80 kJ mol⁻¹; three diffusive domains with an $\ln (D/a^{\mathrm{2}})$ of 8, 6, and 3 s⁻¹; and a fractional contribution of 0.70, 0.27, and 0.03 to the total gas release, respectively. The incorrect but apparent activation energy obtained from a linear regression of the low-temperature heating steps is reported in the legend and fitted using the same data point for all scenarios. The difference in apparent diffusivity and activation energy is solely due to multiple diffusion domains, gas loss during irradiation, and storage time before the step-heating experiment.

As we show in the following sections, our forward MDD model inversion that includes free parameters for storage loss showed that the majority of gas produced in the neutron-irradiated feldspar samples was lost during storage. Because this was unexpected, we conducted an additional experiment in which we measured total ³He and ⁴He concentrations in a set of Fish Canyon sanidine (FCs) samples with different storage durations. For many decades, the FCs grains (Cebula, 1986) have routinely been used as a reference mineral for argon studies (Phillips et al., 2022; see references therein). Therefore, at BGC, neutron-irradiated FCs grains are available from various irradiation batches going back 15 years, which have all experienced comparable irradiation but varying storage duration. To evaluate major gas loss during prolonged storage time for diffusive minerals, we measured the total ³He and ⁴He concentrations in 7 sample sets of grains having experienced between 1.86 and 14.69 years of storage time at ∼21 °C.

2.3.2 Fitting statistics

We compare the observed fractional gas release from the diffusion experiment (f_obs) with that of the predicted (f_pred) MDD forward model using evenly weighted fractional misfit statistics based on the gas released from each heating step, i, and described by the misfit,

$$\begin{array}{}\text{(1)}& M=\sum _{i=\mathrm{1}}^N{\displaystyle \frac{f_{i,\text{obs}}-f_{i,\text{pred}}}{f_{i,\text{obs}}}}.\end{array}$$

We use an evenly weighted fractional misfit, as it is rarely possible to develop a heating schedule in advance of the experiment that releases the same amount of gas in each step; therefore, the released gas amounts and the measurement uncertainties are commonly widely variable among heating steps, and most of the gas is often released in a few steps. Thus, any weighting term based on the measurement uncertainty tends to emphasize the fit to a small minority of the data that have unrepresentatively small uncertainties. A few large, precisely measured heating steps also tend to span a small temperature range, so fitting toward these steps tends to ignore data at other temperatures and bias the estimate of the activation energy (see Sect. 4.1).

The diffusion kinetics is determined by the best fit found using a constrained nonlinear multivariable optimization function (fmincon) within a global search multi-start algorithm, MultiStart (Ugray et al., 2007) in MATLAB, while optimizing for the free parameters: (i) total modeled gas release in atoms, (ii) activation energy, (iii) the diffusion constant for each diffusive domain present, and (iv) the proportional gas releases from each of the domains. When diffusion loss during irradiation and storage is applied to the forward MDD model, the fractional release from these initial steps also becomes free parameters.

The model fitting is constrained by the following: (i) the domains are kept in order, such that $\ln (D_{\mathrm{0}}/a_{\mathrm{1}}{)}^{\mathrm{2}}>\ln (D_{\mathrm{0}}/a_{\mathrm{2}}{)}^{\mathrm{2}}>\mathrm{\dots }>\ln (D_{\mathrm{0}}/a_n{)}^{\mathrm{2}}$ and where n is the number of domains; (ii) the sum of the fractional release from each domain must equal 1, in which the fractional release from each domain must be $>{\mathrm{10}}^{-\mathrm{9}}$, as we consider any less in these domains to be insignificant to the overall diffusion kinetics of the mineral gas release; and (iii) the total predicted gas release results in a complete degassing.

The optimal number of domains is then determined by firstly optimizing the diffusion kinetics for a varying number of domains between 2 and 10. This range is defined by the fact that all the diffusion experiments display nonlinearity; therefore, a single domain cannot explain the data set, and we have not observed step-degassing data sets in which more than 10 domains were needed for fitting. For each domain size, the optimization was repeated 20 times, for which only the minimum misfit results were considered. This is an increase from previous studies (Gorin et al., 2024), due to limited constraints on the diffusion kinetics resulting from storage loss (see Sect. 4.1 for more details). Then we calculate a reduced misfit (similar to a reduced χ²) by dividing the misfit value by the degree of freedom, which is defined by the number of modeled parameters subtracted from the number of data points used in the fitting. The number of modeled domains that result in the lowest reduced misfit value is found to be the optimal number of domains needed to explain the data set without overfitting.

3 Results

3.1 ³He diffusion kinetics in plagioclase

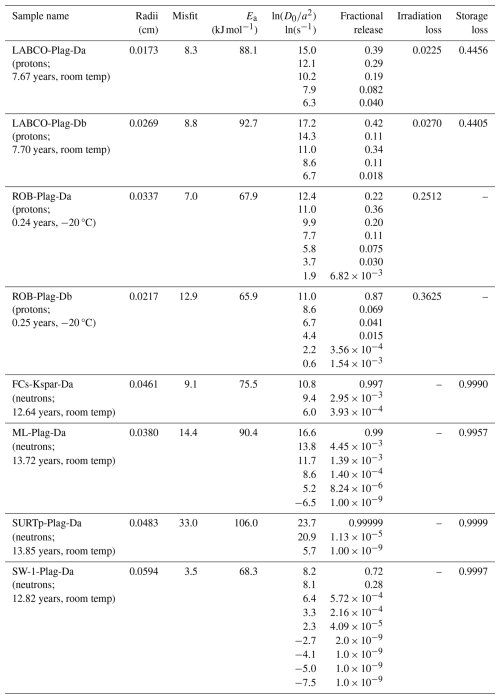
Results for ³He step-heating experiments for the two plagioclase and feldspar sample groups are shown in Table S1 and Fig. 2. All experiments display nonlinear behavior in the Arrhenius plot. For the samples stored at room temperature prior to analysis, there is a consistent increase in apparent diffusivity in isothermal heating steps below 250 °C. This is consistent with gas loss occurring during irradiation and/or storage. The forward-modeled MDD diffusion kinetics are reported in Table 2, and the predicted apparent diffusivity is shown in Figs. 3 and 4.

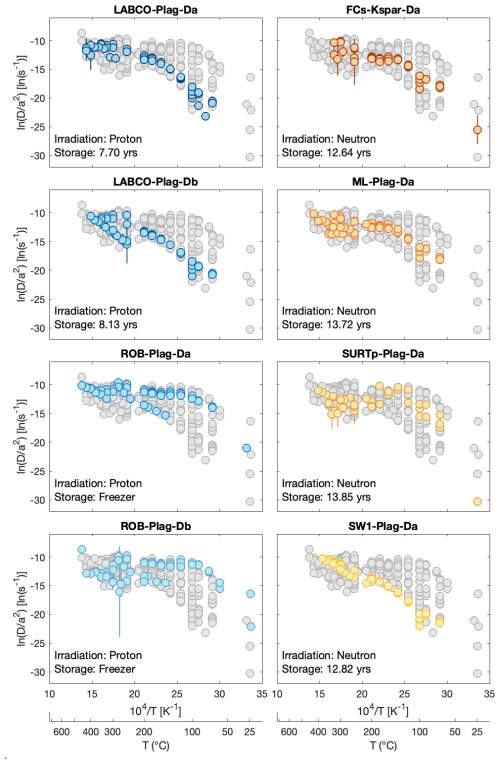
Figure 2 Arrhenius plot for apparent ³He diffusivity in plagioclase grains. Each individual diffusion experiment is plotted in color in its respective panel. Gray data points represent all plagioclase diffusion experiments for comparison. Vertical lines show the uncertainty in $\ln (D/a^{\mathrm{2}})$ and are estimated using error propagation derived by Ginster and Reiners (2018), although the uncertainty is usually smaller than the symbol.

Table 2 Summary of modeled MDD diffusion kinetics results for all feldspar grains.

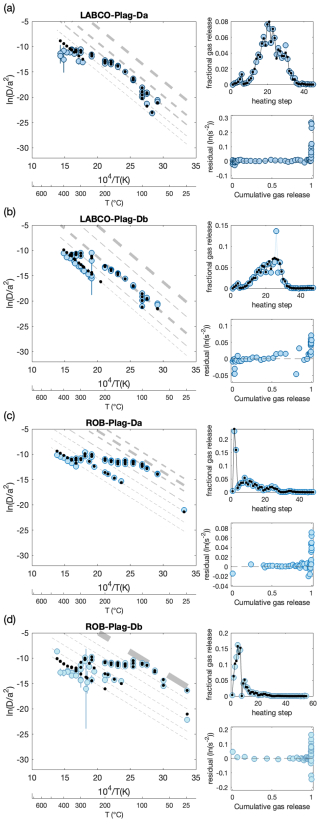
Figure 3 Forward-modeled MDD results for Ferrar Dolerite plagioclase. Each sample result (a–d) is displayed in the Arrhenius, fractional release, and residual plots. Colored circles show the observed apparent ³He diffusivity from the step-heating experiment. Vertical lines show the uncertainty in $\ln (D/a^{\mathrm{2}})$ (see description in Fig. 2 for more details). Black dots show the modeled predicted apparent diffusivity from the best reduced misfit, where the gray lines represent the diffusion kinetics of each individual domain modeled, with the line thickness being proportional to the fractional size of the domain. The fractional release plot compares the measured and predicted fractional gas release from each heating step during the diffusion experiment. The residuals are defined as the difference between the calculated $\ln (D/a^{\mathrm{2}})$ from a given heating step and the expected $\ln (D/a^{\mathrm{2}})$ from the first MDD model domain at that same temperature and are plotted against the cumulative gas release.

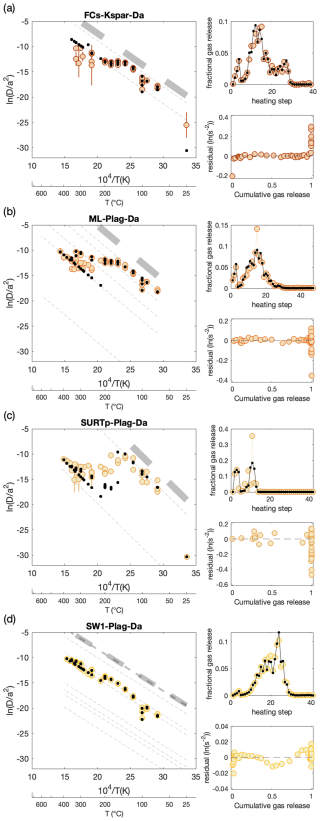
Figure 4 Forward-modeled MDD results for a variety of feldspar compositions. Each sample result (a–d) is displayed in the Arrhenius, fractional release, and residual plots. Colored circles show the observed apparent ³He diffusivity from the step-heating experiment. Vertical lines show the uncertainty in $\ln (D/a^{\mathrm{2}})$ (see description in Fig. 2 for more details). Black dots show the modeled predicted apparent diffusivity from the best reduced misfit, where the gray lines represent the diffusion kinetics of each individual domain modeled, with the line thickness being proportional to the fractional size of the domain. See Fig. 3 for more details on plotting.

The Ferrar Dolerite plagioclase samples, LABCO and ROB, were proton-irradiated; therefore, we account for loss during the irradiation stage for both samples and only include storage loss for the LABCO sample, as ROB was kept frozen (ca. −20 °C) immediately after irradiation. The total modeled irradiation and storage gas loss for LABCO is ∼47 %, of which ∼2.5 % was released during irradiation (Table 2). On the contrary, the ROB samples show 25 %–36 % gas release during irradiation. This variation in the predicted gas loss during irradiation can be attributed to the difference in modeled diffusion kinetics between the two samples, with activation energies of ∼90 kJ mol⁻¹ for LABCO and ∼67 kJ mol⁻¹ for ROB. If the two Ferrar plagioclase grains are comparable, this discrepancy suggests that the model inversion may be compensating for storage loss by adjusting the activation energy, reflecting a potential trade-off between the two free parameters. This is discussed in more detail below.

The sample group consisting of various feldspar grains has been neutron-irradiated. As mentioned in Method, we do not account for loss during neutron irradiation but only consider the gas lost during storage at 21 °C. The Arrhenius behavior and modeled diffusion kinetics for these samples show significant variation depending on the composition. However, the total modeled gas loss during storage exceeds 99 % across all feldspar compositions (Table 2). As a result, the step-degassing experiment for these samples only involved ∼1 % of the total amount of gas that was present at the end of the neutron irradiation.

3.2 ³He diffusion kinetics in pyroxene

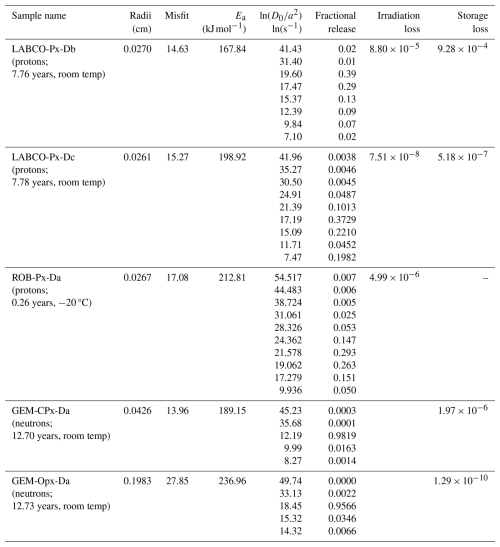
Results from the ³He step-heating experiment applied to two pyroxene sample groups are shown in Table S2 and Fig. 5. All pyroxene samples display nonlinear Arrhenius behavior. While the effect of gas loss during irradiation and storage may be negligible or non-existent for the retentive pyroxene grains, we apply similar modeled irradiation and storage conditions to these samples and to the feldspar samples, as outlined in Table 1. The forward-modeled MDD diffusion kinetics for pyroxene are reported in Table 3 and shown in Figs. 6 and 7.

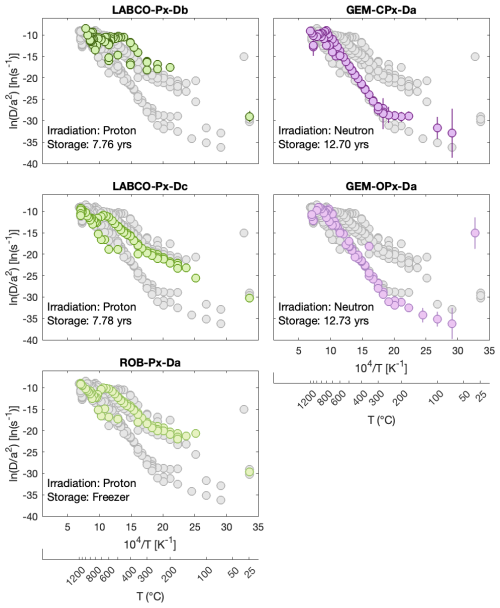
Figure 5 Arrhenius plot for ³He diffusivity in pyroxene grains. Each individual diffusion experiment is plotted in color in its respective panel. Gray data points represent all pyroxene diffusion experiments for comparison. Vertical lines show the uncertainty in $\ln (D/a^{\mathrm{2}})$ and are estimated using error propagation derived by Ginster and Reiners (2018), although the uncertainty is usually smaller than the symbol.

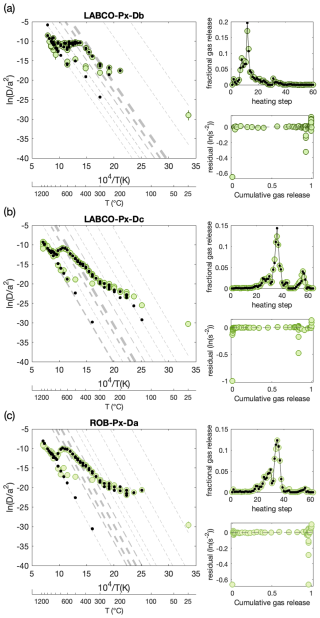
Figure 6 Forward-modeled MDD results for the Ferrar Dolerite pyroxene. Each sample result (a–c) is displayed in the Arrhenius, fractional release, and residual plots. Colored circles show the observed apparent ³He diffusivity from the step-heating experiment. Vertical lines show the uncertainty in $\ln (D/a^{\mathrm{2}})$ (see description in Fig. 5 for more details). Black dots show the modeled predicted apparent diffusivity from the best reduced misfit, where the gray lines represent the diffusion kinetics of each individual domain modeled, with the line thickness being proportional to the fractional size of the domain. See Fig. 3 for more details on plotting.

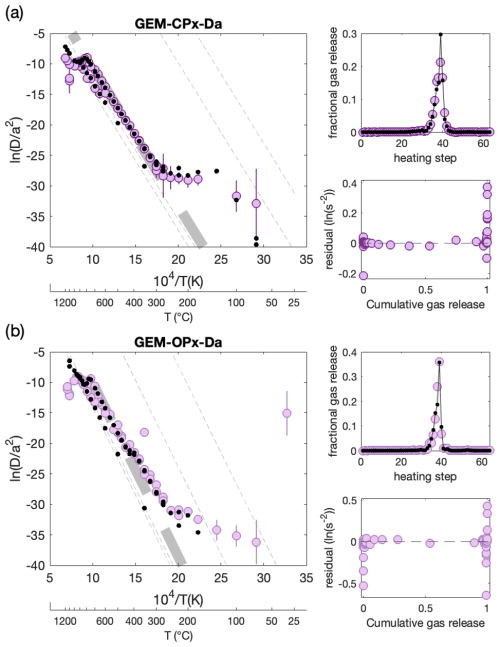
Figure 7 Forward-modeled MDD results for the gem-quality pyroxene. Each sample result (a, b) is displayed in the Arrhenius, fractional release, and residual plots. Colored circles show the observed apparent ³He diffusivity from the step-heating experiment. Vertical lines show the uncertainty in $\ln (D/a^{\mathrm{2}})$ (see description in Fig. 5 for more details). Black dots show the modeled predicted apparent diffusivity from the best reduced misfit, where the gray lines represent the diffusion kinetics of each individual domain modeled, with the line thickness being proportional to the fractional size of the domain. See Fig. 3 for more details on plotting.

Both gem-quality orthopyroxene and clinopyroxene grains show similar diffusion behavior, with the majority of the gas being released in just a few heating steps, resulting in linearity in the Arrhenius plot (Fig. 7). Although the MDD model inversion assumes that all gas at the beginning and end of the diffusion experiment belongs to the same material, which is likely an inaccurate simplification due to natural crystal fragments deviating from perfect spheres (Huber et al., 2011), the model still assigns more than 95 % of the gas to a single domain without being directed by arbitrary data selection. This suggests that both gem-quality pyroxene grains likely exhibit a single domain. In effect, the remaining small domains (<3.5 %) are used as nuisance parameters so that model fitting is not overly restricted by arbitrary data selection.

Table 3 Summary of the modeled MDD diffusion kinetics results for all pyroxene grains.

4 Discussion

4.1 Fitting of the forward MDD model to the data set

The forward MDD model predicts the fractional gas release and apparent diffusion constant for each heating step across a given number of domains for a degassing experiment. Overall, the predicted apparent diffusivity shows good agreement with that observed during the step-heating experiments. However, for the high-temperature heating steps, diffusivity does not align well with the observed data for both plagioclase and pyroxene grains. This discrepancy is primarily due to the fact that the fractional loss from these high-temperature steps accounts for less than 1 % of the total gas release. For example, heating steps 27 to 55 for ROB-Plag-Db (Fig. 3d and Table S1D) contribute only 1 % of the total gas release, making the model fitting statistically insignificant for these steps.

For samples that have experienced prolonged storage periods prior to analysis, the optimized diffusion kinetic parameters become less constrained. We show this in Fig. 8, where a best fit is achieved across a range of activation energies. Previous misfit statistics for MDD inversion models have relied on either fractional misfit, as used in the study, or chi-square misfit (Tremblay et al., 2014b, 2017; Gorin et al., 2024). While both methods effectively constrain the activation energy for samples experiencing minimal initial gas loss (e.g., ROB-Plag), they provide a weaker constraint on the diffusion kinetics for samples having lost significant gas (>25 %; see LABCO-Plag in Table 2). Thus, as expected from the general principle that diffusion is an information-destroying process, gas loss prior to the experiment degrades the ability of a model inversion to correctly estimate diffusion kinetics.

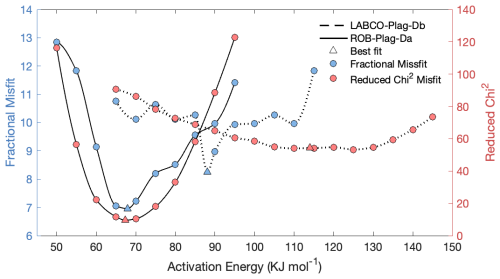
Figure 8 Forward-modeled MDD inversion misfit values for a range of activation energies. To generate these results, the activation energy was fixed at a given value and the model inversion was allowed to optimize all other parameters. Blue dots show the fractional misfit, as used in this study. Red dots show the reduced chi-square misfit value as implemented in previous MDD studies (Gorin et al., 2024). Triangles show the best misfit obtained and displayed in Table 2 for LABCO-Plag-Db (dashed line) and ROB-Plag-Da (solid line).

4.2 Diffusive loss prior to step-heating experiment

4.2.1 Short-term loss during irradiation

It is evident that gas loss from irradiation only affects the apparent diffusivity for the low-temperature heating steps (Fig. 1a). This behavior is observed for the ROB plagioclase samples (Fig. 3c and d), where the first 25 °C heating step has a measurable amount of gas, but the apparent diffusivity is lower than expected if no loss occurred. These samples were kept frozen after irradiation to prevent any diffusive loss of ³He during their short storage time (∼3 months) prior to the step-heating analysis. Consequently, any gas loss prior to analysis is assumed to occur only during irradiation. In the modeled irradiation step, we find that, for example, ROB-Plag-Da has lost 25 % of its gas. Since we do not account for the simultaneous production of ³He gas during irradiation, this is likely an overestimate. If we apply the resulting diffusion kinetics and account for simultaneous production and diffusive loss of ³He during irradiation (using the model for production-diffusion forward simulation; Gribenski et al., 2022), this loss is reduced to 17 %.

One could argue, given the high diffusivity of ROB plagioclase, that gas loss occurs in three stages prior to analysis: (1) irradiation loss, (2) loss during freezer storage, and (3) loss during a 24 h period at room temperature for when the sample is transferred to the mass spectrometer and placed under high vacuum. Therefore, the true gas loss prior to analysis likely falls between the modeled gas loss that includes all three stages and is modeled by excluding the irradiation step. If we exclude irradiation loss and consider only gas loss during the 3-month freezer storage and 24 h of sample transfer to the mass spectrometer at room temperature (two heating steps: −20 °C for 3 months and 21 °C for 24 h), the forward-modeled diffusion kinetics predicts a gas loss of 16 % during freezer storage and 7 % during sample transfer, with a total loss of 23 % and activation energy of 69.2 kJ mol⁻¹. When we include diffusion loss during irradiation (not including production), the modeled gas losses for all three stages are 29 %, 6 %, and 5 %, respectively, with a total loss of 39 % and slightly reduced activation energy of 67.9 kJ mol⁻¹.

The lower apparent diffusivity observed in the first few heating steps, caused by a diffusively rounded profile of ³He in the grain, can be explained by a 23 %–39 % gas loss prior to step-heating analysis and is based on modeled gas loss ranging from simple to complex storage conditions. While the specific contribution of each degassing stage remains unclear, accounting for initial loss and non-homogeneous distribution prior to the diffusion experiment explains the observed gas loss in the initial 25 °C heating step, with negligible effects at temperatures >70 °C. This approach ensures that all data points are used for modeling and constraining the diffusion kinetics.

We acknowledge that assigning diffusion loss to irradiation and/or storage loss may appear arbitrary, as the initial conditions affect the total inferred gas loss. This becomes particularly significant as we lack precision on the temperatures during irradiation and extended storage time. However, the details of the initial gas loss conditions in the model inversion have less of an effect on the activation energy and overall diffusion kinetics. In summary, for samples exhibiting loss reflected as apparent diffusivity in the Arrhenius plot, allowing the forward model to assign an initial gas loss is important for constraining the activation energy. However, the precise allocation of gas for these initial steps within the inversion model is dependent on the gas loss conditions but has less effect on the estimation of the activation energy.

4.2.2 Neutron irradiation complications

For a diffusive mineral, neutron irradiation is expected to result in a non-homogeneous distribution of ³He concentration. Although the exact temperature during neutron irradiation has not been quantified and is therefore not included in the inversion model to predict irradiation loss, it is estimated to reach at least 150 °C during a 50 h irradiation period. Consequently, the simultaneous production and diffusion of ³He and ⁴He likely result in a heterogeneous distribution within the various feldspar grains. When combined with prolonged storage, exceeding 3 years, this leads to >90 % gas loss prior to the diffusion experiment analysis (Fig. 9).

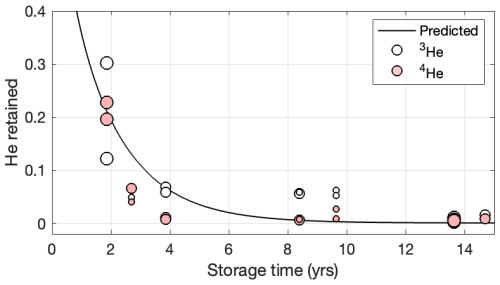
Figure 9 He retention in Fish Canyon sanidine (FCs) grains. The black line shows the ³He retention predicted from the diffusion kinetics modeled for FCs (Table 2). The circles show the observed ³He (white) and ⁴He (red) retention from measured concentrations. The size of the circles is related to the average radius of the grain sizes of the FCs sample analyzed (small: <200 µm; medium: 200–400 µm; large: >400 µm). The measured He concentrations and estimated fractional retention have been normalized to a storage of 1.8 years with a 79 % loss.

As previously mentioned, the model inference of more than 99 % gas loss for the neutron-irradiated samples is unexpected. Thus, to validate this, we measured total ³He and ⁴He concentrations in a series of Fish Canyon sanidine (FCs) grains that experienced varying storage durations (Table S3 in the Supplement).

In Fig. 9, we show He retention in the FCs grains over 15 years of storage. Because we cannot independently estimate the initial He concentration at the end of irradiation, we assume that the samples with the shortest storage time (1.8 years) experienced an average of 79 % gas loss, as predicted by the forward MDD model using the diffusion kinetic for FCs-Plag-Da (Table 2), and back-calculate the initial concentration for all grains on this basis. All samples were neutron-irradiated for a duration of 50 h in the same reactor position. However, the grain size and amount in each sample vary for the 7 samples and therefore contain various sub-grain domains that do not scale with He diffusion. Note that the J-factors obtained from ${}^{\mathrm{39}}\mathrm{Ar}{/}^{\mathrm{40}}\mathrm{Ar}$ analysis of simultaneously irradiated grains are within 3 % of each other. With this normalization, it is evident that the observed decrease in He concentration with storage time conforms to the model-predicted values, and this supports the finding from model inversion of nearly complete gas loss after 12–14 years of storage (Table 2).

The MDD inversion model can compensate storage time for activation energy, thereby reducing the constraints on diffusion kinetic parameters and potentially overestimating the activation energy due to the non-unique inversion solution, as shown in Fig. 8. Furthermore, the MDD inversion model accounts for initial gas loss by assigning a fractional loss to two initially predefined steps within the inversion process. This approach allows the model to account for any heterogeneous distribution reflected by the increased apparent diffusivity observed in repeated low-temperature heating steps during the diffusion experiment. However, the model does not differentiate whether this heterogeneous distribution arises from irradiation, storage, or a combination of both but instead adjusts the assigned fractional loss to match the observed loss. Therefore, lack of constraint on the temperature during neutron irradiation (hence, the temperature assigned to the initial predefined steps) complicates quantifying the fractional loss from neutron irradiation. Consequently, for diffusive minerals and cases where spallogenic-produced nuclides are of interest, proton irradiation is preferred to achieve a more homogenous initial He distribution.

4.2.3 Long-term storage loss and implications

Although the model inversion obtains different activation energies for LABCO and ROB plagioclase (Table 2), we will argue that the modeled activation energy and domain parameters for LABCO are likely inaccurate because any signal from low-retentivity domains has been erased by significant gas loss during prolonged storage. To demonstrate this, we take the best-fit diffusion kinetics results for the ROB-Plag-Da sample (which was frozen) and simulate 7.7 years of extended storage experienced by the LABCO-Plag-Db sample using its step-heating experiment. This forward MDD model simulation predicts the experimental step-degassing results that would have occurred if the ROB sample had the same extended storage history as LABCO. Figure 10 shows that the same diffusion kinetics (from ROB) can produce an experimental result similar to that of LABCO if we include extended storage. If we take this prediction result and invert it using the MDD inversion model, we fail to recover the initial MDD diffusion kinetics parameters for ROB.

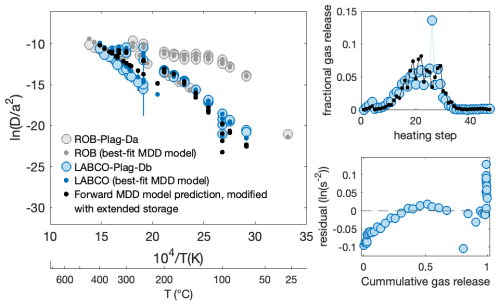
Figure 10 Comparison between the forward-modeled MDD results for the Ferrar Dolerite plagioclase, when including storage loss displayed in the Arrhenius, fractional release, and residual plot (See Fig. 3 for more details on plotting). Circles show the measured apparent diffusivity, and dots represent the forward-modeled predicted apparent diffusivity for LABCO-Plag-Db (blue) and ROB-Plag-Da (grey). Black dots show the predicted apparent diffusivity for LABCO-Plag-Db when applying the diffusion kinetics of ROB-Plag-Da and including initial gas loss during proton irradiation and 7.7 years of storage time at ∼21 °C.

During prolonged storage time, signals from the low-temperature domains can be erased by complete degassing of low-retentive diffusion domains. While the MDD inversion model can account for initial gas and heterogeneous distribution of He during irradiation and storage, it is not able to recover the diffusion kinetics from domains that have been completely degassed, and information has been lost prior to the diffusion experiment. This is evident in the weak constraint on the activation energy, even when accounting for loss during and after irradiation (Fig. 8), leading to a higher apparent activation energy and, overall, an apparently more retentive mineral.

This raises the question of whether the diffusion kinetics from the various feldspar grains (Fig. 4 and Table 2) can be reliably interpreted as being unique to the compositions or if we are observing the effect of completely degassed low-retentive diffusion domains during storage, and therefore overestimating the activation energy and retentivity of ³He in feldspars during inversion.

In summary, this suggests that (i) not including storage loss in the inversion for the diffusion kinetics produces incorrect kinetics, (ii) significant storage loss makes it impossible to get accurate kinetics even with a more complete MDD inversion model, or (iii) both.

4.3 Application of ³He diffusion in plagioclase in paleothermometry

Measured ³He diffusivity on a range of plagioclase compositions shows variable and complex diffusion behaviours. This is reflected in the retentivity of cosmogenic ³He in plagioclase at Earth's surface temperatures, which varies greatly on a timescale <10⁶ years (Fig. 11). Here, we use the inverted MDD diffusion kinetics to model the long-term retentivity of ³He in plagioclase as a function of exposure time and constant effective diffusion temperature (EDT: Tremblay et al., 2017; Christodoulides et al., 1971) for a cold region climate (1 °C), such as polar or high-altitude environments.

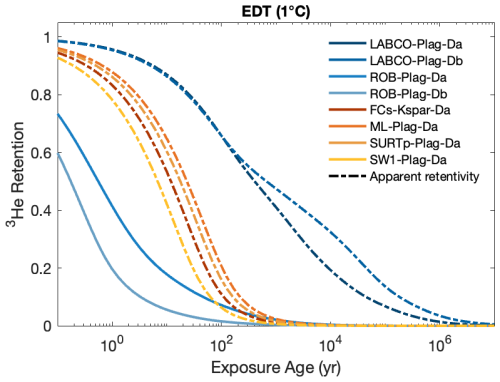
Figure 11 Cosmogenic ³He retention in plagioclase with exposure age for an effective diffusion temperature (EDT) of 1 °C. The ³He retentivity is calculated based on the accumulation-diffusion equation in Wolf et al. (1998) and modified to accept multiple diffusion domains. Solid lines represent diffusion kinetics that are presumed to be accurate representation for the samples. Dashed lines indicate samples where the apparent diffusivity is likely an overestimation due to prolonged storage loss and therefore not a true representation.

The retentivity between the two Ferrar Dolerite samples (LABCO and ROB) displays the largest discrepancy in retentivity. This can, in part, be explained by the signals from the low-temperature domains in LABCO being erased by complete degassing of diffusion domains during storage of the sample at room temperature, as discussed above. As a result, the MDD inversion will overestimate the diffusion kinetics, predicting a higher retentivity. Other factors, such as effective diffusion radius, crystal structure, crystal chemistry, defective density, and state of order, can cause variable diffusivity between the grains of similar mineral groups and compositions (Gourbet et al., 2012). The ROB plagioclase samples are the least retentive and display significant diffusion loss within 100 years. As the ROB plagioclase samples have experienced the least amount of diffusive loss prior to diffusion analysis, the diffusion kinetics are presumed to be accurately represented for those samples. The LABCO plagioclase samples appear to be partially retentive beyond 10³ years at 1 °C and potentially useful as a paleothermometer for cold climate regions. However, the apparent diffusion kinetics for LABCO is potentially an overestimation and, therefore, not a true representation.

Since the loss of ³He during prolonged storage time prior to step-heating analysis can explain the discrepancy between the observed variation in retentivity, it is questionable if cosmogenic ³He is retentive enough in plagioclase to be used as a paleothermometer in polar and high-altitude environments. However, the retention shown in Fig. 11 is specific to the analyzed grain size and has not been normalized. Larger grains corresponding to larger diffusion domains would, therefore, display larger retention, which could be advantageous for ³He diffusivity in plagioclase for paleothermometry.

4.4 Implications of irradiation and storage loss on paleothermometry

In this study, cosmogenic ³He in plagioclase grains is found to be diffusive at Earth's surface temperature and experiences significant diffusive loss on timescales of a hundred years, making it unsuitable as a paleoclimate indicator, even in polar and high-altitude regions with persistent subzero surface temperature. Conversely, cosmogenic ³He in quartz grains has been found to be partly diffusive at Earth's surface temperature on timescales >10³ years at subzero (Tremblay et al., 2014b) and, therefore, applicable to paleothermometry. However, the step-heating data sets from which this is determined all display an increased apparent diffusivity in the Arrhenius trend for the low-temperature heating steps, similar to that observed in plagioclase grains in this study (Fig. 3). The behavior in these first few heating steps was attributed to loss during or after irradiation and excluded from the regression fitting and the retentivity was established from a two-domain MDD model, including two separate activation energies determined from the high- and low-temperature Arrhenius linearity.

As the fitting scheme used by Tremblay et al. (2014b) has some properties (e.g., the use of multiple activation energies) that have the effect of compensating for spuriously low diffusivity in early steps affected by gas loss, we cannot directly compare the result of our MDD model that includes gas loss to the results of Tremblay et al. (2014b). However, we can use our forward MDD model to evaluate the effective magnitude of not including initial gas loss on the application for paleothermometry. Thus, we inverted the step-degassing data of the quartz sample HU-08-03 obtained by Tremblay et al. (2014b) with our (i) forward MDD model inversion lacking irradiation and storage loss, and (ii) forward MDD model inversion including both irradiation and storage loss (See Table S4 and Fig. S3 in the Supplement for details and diffusion kinetic results). This quartz sample was proton-irradiated for 5 h in which the temperature did not exceed 45 °C, and kept in storage at room temperature for 1.3 years between irradiation and step-heating analysis. Further, radiocarbon ages from the moraine on which this sample was collected provide an exposure age of 12 350 $+\mathrm{200}/-\mathrm{20}$ years (Kelly et al., 2012, 2013), with cosmogenic ³He measurements indicating a retentivity of 0.22 ± 0.03.

In Fig. 12, we show that the modeled MDD inversion results, including initial gas loss, predict ³He retention closely matching the observed Holocene value. Contrary, a model inversion lacking initial gas loss greatly overpredicts ³He retention. This effect is most significant for any diffusive mineral that displays increased apparent diffusivity in the Arrhenius trend and resides within a partial retention zone at surface temperatures. While this does not suggest that the diffusion kinetics estimated by Tremblay et al. (2014b) are incorrect (since their fitting approach indirectly compensates for initial gas loss), it does highlight that not accounting for initial gas loss when determining the diffusion kinetics will have a significant effect on the paleothermometry estimates.

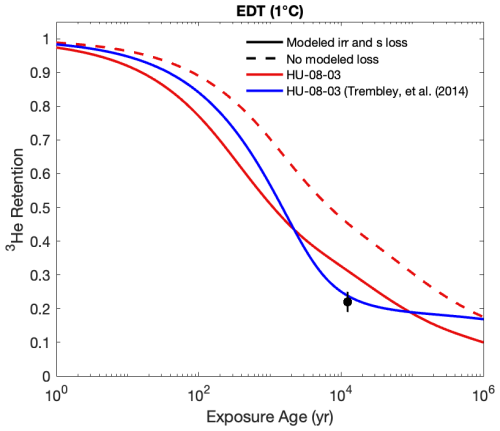
Figure 12 Cosmogenic ³He retention in quartz sample, HU-08-03 (Tremblay et al., 2014b), with exposure age for an effective diffusion temperature (EDT) of 1 °C. The ³He retentivity is calculated based on the accumulation-diffusion equation in Wolf et al. (1998) Wolf et al. (1998) and modified to accept multiple diffusion domains. The black data point shows the observed ³He retentivity in HU-08-03 and its radiocarbon exposure age of 12 350 $+\mathrm{200}/-\mathrm{20}$ years (Kelly et al., 2012, 2013).

4.5 Retentivity of ³He in pyroxene and its implication to exposure-dating

We find the activation energy for cosmogenic ³He diffusion in pyroxene to be 168–237 kJ mol⁻¹. The variability observed in the kinetics among pyroxene samples is less important from the perspective of cosmogenic ³He retention at Earth surface temperatures, as the least retentive pyroxene will retain 95 % of cosmogenic ³He at 50 °C on a timescale of millions of years, and other pyroxenes will retain ≫99 %.

Further, all pyroxene samples are found to be more retentive in cosmogenic ³He, compared to the only known estimates for ⁴He diffusion in pyroxene, which have published activation energies of 116 and 124 kJ mol⁻¹ (Lippolt and Weigel, 1988). While Lippolt and Weigel (1988) found pyroxene to be retentive on a >100 Ma timescale, these lower activation energies were derived from linear regression of low-temperature heating steps. If a similar methodology were applied to the ROB and LABCO pyroxene, those would likely show comparable low activation energies (Fig. 6b and c). The activation energy and retentivity for ³He diffusion are higher in orthopyroxene than in clinopyroxene. While less retentive, this observation is consistent with that observed for cosmogenic ²¹Ne diffusivity in orthopyroxene and clinopyroxene (Gourbet et al., 2012), attributing this difference to the atomic structure of the pyroxene phases.

In Fig. 13, we show the duration and temperature curves that will result in a 10 % diffusive loss of accumulated cosmogenic ³He in the various pyroxene samples. While retentive at Earth's surface temperature, a brief preheating (<1000 s), such as an impact event (Shuster et al., 2010), volcanic activity, or wildfires (Balco et al., 2024), will significantly disturb the cosmogenic ³He concentration for temperatures as low as 400 °C.

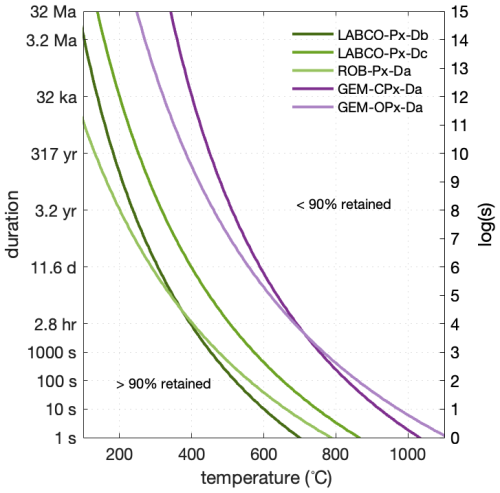
Figure 13 Cosmogenic ³He retention in pyroxene for duration and temperature pairs that predict 10 % diffusive loss of cosmogenic ³He in pyroxene. The retentivity is calculated based on the accumulation-diffusion equation in Wolf et al. (1998) and modified to accept multiple diffusion domains.

Given that few places on Earth have surface temperatures that consistently exceed 50 °C, cosmogenic ³He will generally be quantitatively retained in pyroxene over timescales and temperatures relevant for exposure dating. This is consistent with numerous measurements of cosmogenic ³He exposure ages in pyroxene that show (i) high temperatures are required to extract He from pyroxene and (ii) measured ³He concentrations in pyroxene are consistent with exposure ages determined from other geological evidence (e.g., Kurz, 1986; Schäfer et al., 1999; Balter-Kennedy et al., 2020).

The distinct difference in the retentivity between cosmogenic ³He in pyroxene and plagioclase could be beneficial for exposure dating of ³He in pyroxene. The Antarctic Ferrar dolerite samples consist predominantly of plagioclase and pyroxene, with minor traces of oxides (Harvey, 2001; Elliot and Fleming, 2021). The crystal texture is mostly fine-grained, making the separation and isolation procedure tedious to obtain monomineralic pyroxene grains of 100–500 µm fragments, as often used in cosmogenic nuclide exposure dating. However, as cosmogenic-produced ³He in plagioclase is diffusive at Earth's surface temperature, a separation process may not be necessary as an insignificant amount of ³He is naturally retained in the plagioclase grains. Thus, measuring the concentration of ³He in a piece of whole rock of Ferrar dolerite could be directly converted into a ³He concentration within the pyroxene fragment, eliminating the laboratory procedure for separating and isolating pyroxene grains.

5 Conclusion

In this study, we measured ³He diffusivity in various plagioclase and pyroxene grains through a series of stepwise degassing experiments and applied a “multiple-diffusion-domain” (MDD) inversion model to determine the diffusion kinetics. We find the apparent diffusion kinetics of ³He in plagioclase to be greatly variable. However, this variability can be explained by the MDD inversion models' inability to constrain the diffusion parameters when significant gas has been lost during either irradiation and/or prolonged storage prior to the diffusion experiment. In such cases, the forward MDD model overestimates the activation energy by compensating for storage loss. Further, for diffusive minerals, that incompletely retain He at Earth's surface temperatures, prolonged storage time at room temperature can result in complete degassing of low-retentive domains, limiting the MDD inversion model's ability to constrain the diffusion kinetics. As a result, samples that were kept frozen for a short period of time immediately after irradiation until experimental analysis (ROB-Plag) yielded the most reliable estimate of the activation energy and diffusion parameters. This highlights the importance of (i) limiting storage time between irradiation and analysis, (ii) accounting for any diffusive loss occurring before the diffusion experiment when determining the diffusion kinetics of less retentive minerals, and (iii) freeze samples to limit gas loss during storage time.

Overall, our findings suggest that ³He in plagioclase is diffusive at Earth's surface temperatures on a timescale of hundred years, making it unsuitable for paleothermometry. On the contrary, pyroxene retains cosmogenic ³He at Earth's surface temperatures over millions of years, though brief preheating (<1000 s) could significantly disturb its concentration. The distinct difference in cosmogenic ³He retentivity between pyroxene and plagioclase could, however, be beneficial for exposure dating of ³He in mafic rock consisting predominantly of pyroxene and plagioclase.