An algorithm for U–Pb geochronology by secondary ion mass spectrometry

Secondary ion mass spectrometry (SIMS) is a widely used technique for in situ U–Pb geochronology of accessory minerals. Existing algorithms for SIMS data reduction and error propagation make a number of simplifying assumptions that degrade the precision and accuracy of the resulting U–Pb dates. This paper uses an entirely new approach to SIMS data processing that introduces the following improvements over previous algorithms. First, it treats SIMS measurements as compositional data using log-ratio statistics. This means that, unlike existing algorithms, (a) its isotopic ratio estimates are guaranteed to be strictly positive numbers, (b) identical results are obtained regardless of whether data are processed as normal ratios (e.g. ²⁰⁶Pb $/$ ²³⁸U) or reciprocal ratios (e.g. ²³⁸U $/$ ²⁰⁶Pb), and (c) its uncertainty estimates account for the positive skewness of measured isotopic ratio distributions. Second, the new algorithm accounts for the Poisson noise that characterises secondary electron multiplier (SEM) detectors. By fitting the SEM signals using the method of maximum likelihood, it naturally handles low-intensity ion beams, in which zero-count signals are common. Third, the new algorithm casts the data reduction process in a matrix format and thereby captures all sources of systematic uncertainty. These include significant inter-spot error correlations that arise from the Pb $/$ U–UO₍₂₎ $/$ U calibration curve. The new algorithm has been implemented in a new software package called simplex. The simplex package was written in R and can be used either online, offline, or from the command line. The programme can handle SIMS data from both Cameca and SHRIMP instruments.

1 Introduction

Secondary ion mass spectrometry (SIMS) combines high sensitivity with high mass resolution (Williams, 1998). This allows the technique to obtain precise U–Pb dates on nanogram-sized samples whilst resolving isobaric interferences on ²⁰⁴Pb to a degree that is currently unachievable by other techniques such as laser ablation inductively coupled plasma mass spectrometry (LAICPMS). There are some other differences between LAICPMS and SIMS as well. LAICPMS instrumentation is built by numerous manufacturers, whose data files are compatible with a rich ecosystem of data reduction codes such as Iolite, Glitter, and LADR. This facilitates the intercomparison of different laboratories, different instrument designs, and so forth. In contrast, the SIMS U–Pb world is dominated by just two manufacturers, whose SHRIMP (Sensitive High Resolution Ion Micro-Probe) and Cameca instruments use completely separate data reduction protocols. Most SHRIMP laboratories use Squid (Ludwig, 2000; Bodorkos et al., 2020), which is incompatible with Cameca data. In contrast, Cameca data tend to be processed by in-house software such as Martin John​​​​​​​ Whitehouse's NordSIM spreadsheet, which are incompatible with SHRIMP data.

This paper introduces a unified algorithm for SIMS U–Pb data reduction that aims to address five problems with existing data reduction methods. The first three of these problems are the following.

• 1.

  Accuracy: existing algorithms give (slightly) different results depending on whether the raw data are processed as ²⁰⁶Pb $/$ ²³⁸U ratios or as ²³⁸U $/$ ²⁰⁶Pb ratios.

• 2.

  Precision: current data reduction routines produce symmetric confidence intervals, which are unrealistic for low-intensity ion beams.

• 3.

  Systematic uncertainties: current data reduction protocols use a hierarchical error propagation approach, in which random uncertainties and systematic uncertainties are propagated separately. However, such a clean separation is not always possible, and this can complicate higher-order data processing steps such as isochron regression and averaging.

Sections 2–4 will provide further details about these problems using synthetic examples. Section 5 will show that problems 1, 2, and 3 can be solved by treating the U–Pb system as a compositional data space using log-ratio statistics. However, log-ratio statistics do not solve the remaining two problems.

• 4.

  Backgrounds: background correction of low-intensity signals such as ²⁰⁴Pb sometimes exceeds 100 %, producing physically impossible negative isotope ratios.

• 5.

  Zeros: Pb isotopes are usually measured by secondary electron multipliers (SEMs), which record ions as counts. For ²⁰⁴Pb and other low-intensity ion species, it is not uncommon to register zero counts during any given analytical cycle. This causes problems if the zero count appears in the denominator of an isotopic ratio.

These problems are discussed in more detail in Sect. 6. Section 7 addresses them by incorporating multinomial counting statistics into the compositional data framework. Sections 8–11 recast the U–Pb processing chain in this mixed multinomial–compositional form. Section 12 applies the new data reduction paradigm to two datasets produced by Cameca and SHRIMP instruments, and Sect. 13 introduces a computer code called simplex that generated these results. Finally, further details about the implementation of the new algorithm are reported in the Appendix to this paper.

2 Accuracy

The common Pb-corrected ²⁰⁶Pb $/$ ²³⁸U age (t) depends on the relative abundances of the three nuclides ²⁰⁴Pb, ²⁰⁶Pb, and ²³⁸U:

$$\begin{array}{}\text{(1)}& t={\displaystyle \frac{\mathrm{1}}{{\mathit{\lambda }}_{\mathrm{238}}}}\ln \left(\mathrm{1}+{\displaystyle \frac{\left[\frac{{}^{\mathrm{206}}\mathrm{Pb}}{{}^{\mathrm{204}}\mathrm{Pb}}\right]-{\left[\frac{{}^{\mathrm{206}}\mathrm{Pb}}{{}^{\mathrm{204}}\mathrm{Pb}}\right]}_{\mathrm{c}}}{\left[\frac{{}^{\mathrm{238}}\mathrm{U}}{{}^{\mathrm{204}}\mathrm{Pb}}\right]}}\right),\end{array}$$

where the subscript c marks the common lead composition, and λ₂₃₈ is the decay constant of ²³⁸U. Equation (1) does not depend on the absolute amounts of ²⁰⁴Pb, ²⁰⁶Pb, and ²³⁸U, but only on their ratios. Unfortunately, the statistical analysis of the ratios of strictly positive numbers is full of potential pitfalls, as will be illustrated with an example that was inspired by McLean et al. (2016). Consider a simple dataset of 10 synthetic U–Pb measurements (Table 1).

Table 1 A synthetic U–Pb dataset in arbitrary units (e.g. fmol, mV, pA, or kHz).

Let us calculate the ²⁰⁶Pb $/$ ²³⁸U ratios for these data, which are needed to solve Eq. (1). Comparing these ratios with their reciprocals yields two new sets of 10 numbers.

The elementary rules of mathematics dictate that $\mathrm{1}/(y/x)=x/y$ for any two real numbers x and y. In other words, the reciprocal of the reciprocal ratio ought to equal that ratio. Indeed, for our example it is easy to see that $\mathrm{1}/\mathrm{0.085}=\mathrm{11.70}$ and so forth. However, when we take the arithmetic means of the (reciprocal) ratios

$${\left(\stackrel{\mathrm{‾}}{{}^{\mathrm{206}}\mathrm{Pb}/{}^{\mathrm{238}}\mathrm{U}}\right)}_{\mathrm{a}}=\sum _{i=\mathrm{1}}^{\mathrm{10}}{\left({}^{\mathrm{206}}\mathrm{Pb}/{}^{\mathrm{238}}\mathrm{U}\right)}_i/\mathrm{10}=\mathrm{0.166}$$

and

$${\left(\stackrel{\mathrm{‾}}{{}^{\mathrm{238}}\mathrm{U}/{}^{\mathrm{206}}\mathrm{Pb}}\right)}_{\mathrm{a}}=\sum _{i=\mathrm{1}}^{\mathrm{10}}{\left({}^{\mathrm{238}}\mathrm{U}/{}^{\mathrm{206}}\mathrm{Pb}\right)}_i/\mathrm{10}=\mathrm{9.14},$$

then we find that

$${\displaystyle \frac{\mathrm{1}}{{\left(\stackrel{\mathrm{‾}}{{}^{\mathrm{206}}\mathrm{Pb}/{}^{\mathrm{238}}\mathrm{U}}\right)}_{\mathrm{a}}}}={\displaystyle \frac{\mathrm{1}}{\mathrm{0.166}}}=\mathrm{6.01}\ne \mathrm{9.14}={\left(\stackrel{\mathrm{‾}}{{}^{\mathrm{238}}\mathrm{U}/{}^{\mathrm{206}}\mathrm{Pb}}\right)}_{\mathrm{a}}.$$

So the reciprocal of the mean reciprocal ratio does not equal the mean of that ratio! This is a counter-intuitive and clearly wrong result. Unfortunately, current algorithms for SIMS data reduction average ratios using the arithmetic mean or perform (linear) regression through ratio data, which causes similar problems (Ogliore et al., 2011). Inaccurate ²⁰⁶Pb $/$ ²³⁸U ratios inevitably result in inaccurate U–Pb dates, with the degree of inaccuracy scaling with the relative standard deviation of the measured data. Therefore, the numerical example shown in this section is deeply troubling for isotope geochemistry in general and SIMS U–Pb geochronology in particular.

3 Precision

Traditionally, the precision of isotopic data used in U–Pb geochronology has been calculated as symmetric confidence intervals. Unfortunately, this is fraught with similar problems as those discussed in Sect. 2. For example, take the arithmetic mean ($\stackrel{\mathrm{‾}}{x}$) and standard deviation (s_x) of the ²⁰⁶Pb $/$ ²⁰⁴Pb ratios in Table 1 and construct a Studentised 95 % confidence interval for $\stackrel{\mathrm{‾}}{x}$.



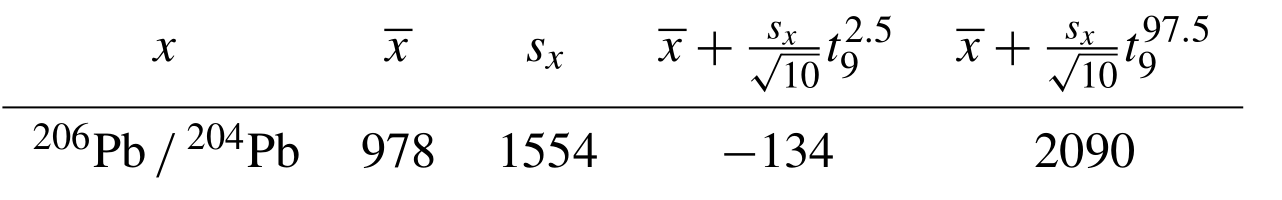
Here, $t_{\mathrm{df}}^{\mathit{\alpha }}$ is the α percentile of a t distribution with df degrees of freedom (e.g. $t_{\mathrm{9}}^{\mathrm{2.5}}=-\mathrm{2.262}$). Then the lower limit of the confidence interval is negative. This nonsensical result is yet another indication that there are some fundamental problems with the application of “conventional” statistical operations to isotopic data. Negative isotope ratios can also arise from background corrections, but this will be further discussed in Section 6.

4 Systematic errors

The statistical uncertainty of analytical data can be classified into two components (Renne et al., 1998).

1. Random (or internal) errors are caused by electronic noise in the ion detectors, counting statistics, and/or temporal variability of the background as a result of changes in the lab environment, for example. They are independent for different aliquots of the same sample and can be quantified by taking replicate measurements. The standard error of these measurements ($\mathit{\sigma }/\sqrt{N}$, where σ is the standard deviation of N replicate measurements) is a measure of their precision. The standard error can be reduced to arbitrarily low levels by simply averaging more measurements (i.e. by increasing N). For example, the precision of SIMS ²⁰⁶Pb $/$ ²⁰⁴Pb ratio measurements can be increased by simply extending the duration of the primary ion bombardment.

2. Systematic (or external) errors include the effects of decay constant uncertainty and the ²⁰⁶Pb $/$ ²³⁸U ratio of reference materials. Getting these constants wrong causes bias in some or all of the measurements and thus affects the accuracy of the age determinations. As their name suggests, the systematic uncertainties are not independent but correlated between different aliquots and samples. They cannot be reduced by simple averaging.

Great care must be taken in choosing which sources of uncertainty should or should not be included in the error propagation. In some cases, inter-sample comparisons of SIMS U–Pb data may legitimately ignore systematic uncertainties. However, when comparing data acquired by different methods, both random and some systematic uncertainties must be accounted for. For example, when comparing U–Pb and ⁴⁰Ar $/$ ³⁹Ar data, the decay constant uncertainty must be propagated, and when comparing SIMS and TIMS U–Pb data, SIMS primary standard age uncertainty and the TIMS tracer uncertainty must be propagated. The conventional way to tackle inter-sample comparisons is called “hierarchical” error propagation (Renne et al., 1998; Min et al., 2000; Horstwood et al., 2016). Under this paradigm, the random uncertainties are processed first and the systematic uncertainties afterwards.

Hierarchical error propagation is straightforward in principle but not always in practice. Some processing steps are of a hybrid nature, including both systematic and random uncertainties. ²⁰⁶Pb $/$ ²³⁸U calibration for SIMS is a good example of this. ²⁰⁶Pb $/$ ²³⁸U ratios are sensitive to elemental fractionation in SIMS analysis (see Sect. 10 for further details). These fractionation effects are captured by the following power law (Williams, 1998; Jeon and Whitehouse, 2015):

$$\begin{array}{}\text{(2)}& \ln {\left[{\displaystyle \frac{{{}^{\mathrm{206}}\mathrm{Pb}}^{+}}{{{}^{\mathrm{238}}\mathrm{U}}^{+}}}\right]}_{\mathrm{m}}=A+B\ln {\left[{\displaystyle \frac{{}^{\mathrm{238}}\mathrm{U}{}^{\mathrm{16}}{\mathrm{O}}_{\left(\mathrm{2}\right)}^{+}}{{{}^{\mathrm{238}}\mathrm{U}}^{+}}}\right]}_{\mathrm{m}},\end{array}$$

where the subscript m stands for the measured signal ratio, which is generally different from the atomic ratio, and the subscript (2) refers to the fact that the calibration normally uses uranium oxide for SHRIMP and uranium dioxide for Cameca instruments. The atomic ²⁰⁶Pb $/$ ²³⁸U log ratio of a sample is determined by (1) determining the intercept (A) and slope (B) of a reference material (r) of known Pb $/$ U ratio¹ and (2) using this calibration curve to estimate the equivalent Pb $/$ U log ratio of the reference material corresponding to the UO₍₂₎ $/$ U log ratio of the sample (s). Then,

$$\begin{array}{}\text{(3)}& \begin{array}{rl}\ln {\left[{\displaystyle \frac{{}^{\mathrm{206}}\mathrm{Pb}}{{}^{\mathrm{238}}\mathrm{U}}}\right]}_{\mathrm{a}}^{\mathrm{s}}& =\ln {\left[{\displaystyle \frac{{}^{\mathrm{206}}\mathrm{Pb}}{{}^{\mathrm{238}}\mathrm{U}}}\right]}_{\mathrm{a}}^{\mathrm{r}}+\ln {\left[{\displaystyle \frac{{{}^{\mathrm{206}}\mathrm{Pb}}^{+}}{{{}^{\mathrm{238}}\mathrm{U}}^{+}}}\right]}_{\mathrm{m}}^{\mathrm{s}}\\ & -A-B\ln {\left[{\displaystyle \frac{{}^{\mathrm{238}}\mathrm{U}{{}^{\mathrm{16}}\mathrm{O}}_{\left(\mathrm{2}\right)}^{+}}{{{}^{\mathrm{238}}\mathrm{U}}^{+}}}\right]}_{\mathrm{m}}^{\mathrm{s}},\end{array}\end{array}$$

where the subscript “a” stands for the estimated (for the sample) or known (for the reference material) atomic log ratios. The analytical uncertainty of $\ln {\left[{}^{\mathrm{206}}\mathrm{Pb}/{}^{\mathrm{238}}\mathrm{U}\right]}_{\mathrm{a}}^{\mathrm{s}}$ depends on the analytical uncertainties of both the intercept (A) and slope (B) of the reference material. But it does not necessarily do so to the same degree for all aliquots. Analytical spots that have similar UO₍₂₎ $/$ U ratios as the reference material will be less affected by the uncertainty of the reference material fit than spots that have very different UO₍₂₎ $/$ U ratios (Fig. 1). Hence, it is not possible to make a clean separation between random and systematic uncertainties.

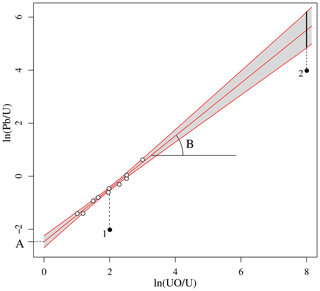
Figure 1 SIMS U–Pb calibration curve. White circles mark the isotopic measurements of the reference material and black circles those of two aliquots of the same sample. The uncertainty of the linear fit is shown as a 95 % confidence interval (grey area). This uncertainty can be propagated into the Pb $/$ U composition of the sample. It is a systematic uncertainty in the sense that it affects both aliquots. But it does not do so to the same degree. The calibration uncertainty of aliquot 2 is greater than that of aliquot 1 due to its horizontal offset relative to the calibration data.

5 U–Pb geochronology as a compositional data problem

Section 2 pointed out that the U–Pb age equation (Eq. 1) does not depend on the absolute amounts of ²⁰⁴Pb, ²⁰⁶Pb, and ²³⁸U, but only on their relative abundances. Thus, we could normalise the ²⁰⁴Pb, ²⁰⁶Pb, and ²³⁸U measurements of Table 1 to unity and plot them on a ternary diagram. The same is true for other geochronometers such as U–Th–He and ⁴⁰Ar $/$ ³⁹Ar (Vermeesch, 2010, 2015). In mathematics, the ternary sample space is known as a two-dimensional simplex. Data that live within this type of space are called compositional data.

Ternary systems are common in igneous petrology (e.g. the A–F–M diagram) and sedimentary petrography (e.g. the Q–F–L diagram). Geologists have long been aware of the problems associated with averages, confidence regions, and linear regression in these closed data spaces (Chayes, 1949, 1960). But a general solution to this conundrum was not found until the 1980s, when the Scottish statistician John Aitchison published a landmark paper and book on the subject (Aitchison, 1982, 1986).

In this work, Aitchison proved that all the problems associated with the statistical analysis of compositional data can be solved by mapping those data from the simplex to a Euclidean space by means of an additive log-ratio (ALR) transformation. For example, given the ternary system $\mathit{\{}x,y,z\mathit{\}}$, we can define two new variables {u,v} so that

$$u=\ln (x/z)$$

and

$$\begin{array}{}\text{(4)}& v=\ln (y/z).\end{array}$$

In this space, Aitchison showed, one can safely calculate averages and confidence limits. Once the statistical analysis of the transformed data has been completed, the results can then be mapped back to the simplex by means of an inverse log-ratio transformation:

$$x={\displaystyle \frac{e^u}{\mathrm{1}+e^u+e^v}},y={\displaystyle \frac{e^v}{\mathrm{1}+e^u+e^v}}$$

and

$$\begin{array}{}\text{(5)}& z={\displaystyle \frac{\mathrm{1}}{\mathrm{1}+e^u+e^v}}.\end{array}$$

For example, the ^204,6Pb–²³⁸U system of Table 1 can be mapped from the ternary diagram to a bivariate $\ln ({}^{\mathrm{204}}\mathrm{Pb}/{}^{\mathrm{238}}\mathrm{U})$–$\ln ({}^{\mathrm{206}}\mathrm{U}/{}^{\mathrm{238}}\mathrm{U})$ space.


Alternatively, we could also use ²⁰⁶Pb as the denominator isotope.


Calculating the average of the transformed data and mapping the results back to the simplex using the inverse log-ratio transformation yields the geometric mean of the ratios:

$${\left(\stackrel{\mathrm{‾}}{{}^{\mathrm{238}}\mathrm{U}/{}^{\mathrm{206}}\mathrm{Pb}}\right)}_{\mathrm{g}}=\mathrm{7.58}={\displaystyle \frac{\mathrm{1}}{\mathrm{0.13}}}={\displaystyle \frac{\mathrm{1}}{{\left(\stackrel{\mathrm{‾}}{{}^{\mathrm{206}}\mathrm{Pb}/{}^{\mathrm{238}}\mathrm{U}}\right)}_{\mathrm{g}}}},$$

which is an altogether more satisfying result than in Sect. 2. Moving on to the 95 % confidence intervals of the ²⁰⁶Pb $/$ ²⁰⁴Pb ratios, we first determine the conventional confidence limits for the log ratios.

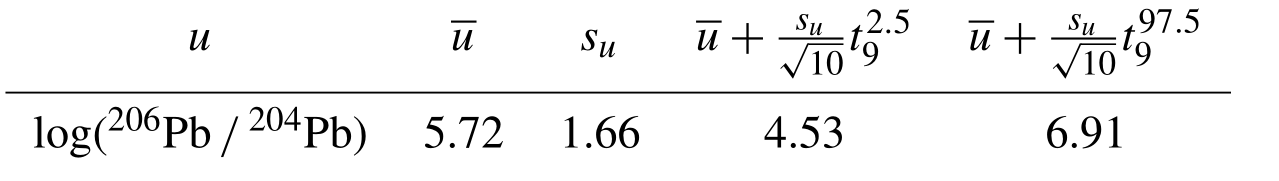
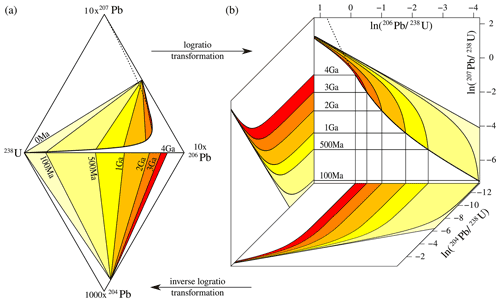
Figure 2 The U–Pb age equation (a) projected onto the four-component simplex and (b) mapped to a three-dimensional Euclidean log-ratio space. ²³⁵U is omitted from the diagrams because it exists in a constant ratio to ²³⁸U (²³⁸U $/$ ²³⁵U = 137.818, Hiess et al., 2012). The boundaries between the coloured regions mark mixing lines between radiogenic and inherited end-member compositions, assuming common Pb ratios of [²⁰⁷Pb $/$ ²⁰⁴Pb]_c = 10 and [²⁰⁶Pb $/$ ²⁰⁴Pb]_c = 9. The mixing lines define isochron surfaces that are linear in the simplex and curved in log-ratio space. Rotating the log-ratio plot 90^∘ clockwise produces a logarithmic version of the familiar Wetherill concordia diagram. Concordant ²⁰⁶Pb $/$ ²³⁸U and ²⁰⁷Pb $/$ ²³⁵U compositions are marked by a thick black line from 0 to 4 Ga and by a dotted line beyond 4 Ga. This paper makes the case that U–Pb data processing is best done in log-ratio space because this “liberates” the data from the geometric constraints of the simplex, producing symmetric uncertainty distributions and more accurate results.

After the inverse log-ratio transformation, these values produce an asymmetric 95 % confidence interval for the geometric mean ²⁰⁶Pb $/$ ²⁰⁴Pb ratio of ${\mathrm{305}}_{-\mathrm{212}}^{+\mathrm{695}}$. This interval contains only strictly positive values, solving the problem of Sect. 3. The ALR transformation of Eq. (4) can easily be generalised to more than three components. For example, if ²⁰⁷Pb is added to the mix, then the four-component ${}^{\mathrm{204}\left|\mathrm{6}\right|\mathrm{7}}$Pb–²³⁸U system can be mapped to the three-component $\ln ({}^{\mathrm{204}\left|\mathrm{6}\right|\mathrm{7}}\mathrm{Pb}/{}^{\mathrm{238}}\mathrm{U})$ space (Fig. 2).

The compositional nature of isotopic data embeds a covariant structure into the very DNA of geochronology: in a K-component system, increasing the absolute amount of one of the components automatically lowers the relative amount of the remaining (K−1) components (Chayes, 1960). To deal with this phenomenon, it is customary in compositional data analysis to process data in matrix form using the full covariance matrix. For example, four components yield three log ratios, which require a 3×3 covariance matrix to describe the uncertainties and uncertainty correlations.

This approach is now widely used in sedimentary geology, geochemistry, and ecology (e.g. Weltje, 2002; Vermeesch, 2006; Pawlowsky-Glahn and Buccianti, 2011), and it has recently been adopted for geochronological applications as well (Vermeesch, 2010, 2015; McLean et al., 2016). The log-ratio covariance matrix approach is also uniquely suited to capture the systematic uncertainties (i.e. the inter-spot error correlations) that are produced by the SIMS U–Pb calibration procedure (Sect. 4). In that case, the covariance matrix must be expanded to accommodate multiple spots (e.g. Vermeesch, 2015). For example, the covariance structure of three spots in a four-component system can be captured in a 9×9 matrix.

In conclusion, the log-ratio transformation solves the statistical woes described in Sects. 2, 3, and 4 of this paper. However, there are two additional problems that require further remediation.

6 Background correction

Many mathematical operations are easier in logarithmic space than in linear space: multiplication becomes addition, division becomes subtraction, and exponentiation becomes multiplication. These mathematical operations are very common in mass spectrometer data processing chains (Vermeesch, 2015). However, there are exceptions. For example, background correction does not involve the multiplication but subtraction of two signals. For low-intensity ion beams such as ²⁰⁴Pb, it is possible, by chance, that the background exceeds the signal. This results in negative values of which one cannot take the logarithm.

The subtraction problem can be solved by using a different logarithmic change of variables:

$$\begin{array}{}\text{(6)}& {\mathit{\beta }}_x^y\equiv \ln \left({\displaystyle \frac{y-b}{x-b}}\right),\end{array}$$

where x and y are the signals and b is the background. The infinite space of ${\mathit{\beta }}_x^y$ covers all possible values of x, y, and b for which x>b and y>b. Thus, background correction should be done in β space, given an appropriate error model as described in Sect. 7.

One caveat to this background correction method is that it does not account for isobaric interferences, which may result in “overcounted” signals. The high mass resolution of SIMS instruments removes most but not all isobaric interferences. For example, spurious HfSi, REE dioxide, or long-chain hydrocarbon ions can interfere with ²⁰⁴Pb, which is generally the rarest isotopic species detected. If unaccounted for, these interferences lead to the proportion of non-radiogenic Pb being overestimated (and the proportion of radiogenic Pb underestimated), resulting in excessive common Pb corrections and underestimated dates. The accuracy of the background measurements can be monitored via the use of isotopically homogeneous reference materials (Black, 2005). A correction can then be applied by choosing the “session blank” that brings the common Pb-corrected ²⁰⁷Pb $/$ ²⁰⁶Pb ratios in alignment with the reference values.

Another issue arises when SIMS signals are registered by secondary electron multiplier (SEM) detectors. These record ion beams as discrete counts, i.e. as integers, which are incompatible with the log-ratio transformation. For example, it is not uncommon for SEM detectors to register zero counts for low-intensity ion beams such as ²⁰⁴Pb. These zero counts blow up the log-ratio transformation because $\ln \left(\mathrm{0}\right)=-\mathrm{\infty }$.

This and other issues are diagnostic of a fundamental difference between compositional data and counting data that has been previously recognised and solved in fission-track dating (Galbraith, 2005) and in sedimentary petrography (Vermeesch, 2018b). The same solutions can be applied to mass spectrometric count data in general and to U–Pb geochronology in particular (Sect. 7).

7 Dealing with count data

Standard data reduction procedures for geochronology assume normally distributed residuals. In compositional data analysis, these are replaced by logistic normal distributions. However, neither the normal nor the logistic normal distribution is perfectly suited to dealing with discrete count data. The multinomial distribution is a simple alternative that seems more appropriate for the task at hand. Before we proceed, let us define the following variables.

• ϕ_x and ϕ_b are the normalised true ion beam intensities (in counts per second) of mass x (from a set of monitored masses 𝕩) and the normalised background signal, respectively, so that

  $$\begin{array}{}\text{(7)}& {\mathit{\varphi }}_b+\sum _{x\in \mathbb{x}}{\mathit{\varphi }}_x=\mathrm{1}\end{array}$$

• d_x and d_b are the dwell times of mass x and the background b

• θ_x and θ_b are the normalised expected beam counts of the ions and the background so that

  $$\begin{array}{}\text{(8)}& {\mathit{\theta }}_x={\displaystyle \frac{{\mathit{\varphi }}_x{d}_x}{{\mathit{\varphi }}_b{d}_b+{\sum }_{y\in \mathbb{x}}{\mathit{\varphi }}_y{d}_y}}\end{array}$$

  and

  $$\begin{array}{}\text{(9)}& {\mathit{\theta }}_b+\sum _{x\in \mathbb{x}}{\mathit{\theta }}_x=\mathrm{1}\end{array}$$

Using the ²⁰⁴Pb $/$ ²⁰⁶Pb ratio as an example, the probability of observing n₄ counts at mass 204, n₆ counts at mass 206, and n_b counts of background is given by

$$\begin{array}{}\text{(10)}& p(n_{\mathrm{4}},n_{\mathrm{6}},n_b|{\mathit{\theta }}_{\mathrm{4}},{\mathit{\theta }}_{\mathrm{6}},{\mathit{\theta }}_b)={\displaystyle \frac{(n_{\mathrm{4}}+n_{\mathrm{6}}+n_b)\mathrm{!}}{n_{\mathrm{4}}\mathrm{!}{n}_{\mathrm{6}}\mathrm{!}{n}_b\mathrm{!}}}{\mathit{\theta }}_{\mathrm{4}}^{n_{\mathrm{4}}}{\mathit{\theta }}_{\mathrm{6}}^{n_{\mathrm{6}}}{\mathit{\theta }}_b^{n_b}.\end{array}$$

Whereas the observations n₄, n₆, and n_b are integers, the parameters θ₄, θ₆, and θ_b are decimal numbers that are constrained to a constant sum. In other words, they belong to the simplex. Thus, we can map the three multinomial parameters to two log-ratio parameters, thereby establishing a natural link between counting data and compositional data. For example,

$$\begin{array}{}\text{(11)}& {\mathit{\beta }}_{\mathrm{6}}^{\mathrm{4}}\equiv \ln \left({\displaystyle \frac{{\mathit{\varphi }}_{\mathrm{4}}-{\mathit{\varphi }}_b}{{\mathit{\varphi }}_{\mathrm{6}}-{\mathit{\varphi }}_b}}\right)=\ln \left({\displaystyle \frac{{\mathit{\theta }}_{\mathrm{4}}/d_{\mathrm{4}}-{\mathit{\theta }}_b/d_b}{{\mathit{\theta }}_{\mathrm{6}}/d_{\mathrm{6}}-{\mathit{\theta }}_b/d_b}}\right)\end{array}$$

and

$$\begin{array}{}\text{(12)}& {\mathit{\beta }}_{\mathrm{6}}^b\equiv \ln \left({\displaystyle \frac{{\mathit{\varphi }}_b}{{\mathit{\varphi }}_{\mathrm{6}}-{\mathit{\varphi }}_b}}\right)=\ln \left({\displaystyle \frac{{\mathit{\theta }}_b/d_b}{{\mathit{\theta }}_{\mathrm{6}}/d_{\mathrm{6}}-{\mathit{\theta }}_b/d_b}}\right).\end{array}$$

${\mathit{\beta }}_{\mathrm{6}}^{\mathrm{4}}$ and ${\mathit{\beta }}_{\mathrm{6}}^b$ can be estimated from n₄, n₆, and n_b by maximising the likelihood defined by Eq. (10).

The normal and logistic normal distributions are controlled by two sets of parameters: location parameters and shape parameters. In the case of the normal distribution, the location parameter is the mean and the shape parameter is the standard deviation (or covariance matrix). In contrast, the multinomial distribution has only one set of (θ) parameters. The precision of multinomial counts is governed by the number of observed counts ($\mathit{\sigma }\left[n\right]=\sqrt{n}$). More sophisticated models are possible when the observed dispersion of the data exceeds that which is expected from the multinomial counting statistics (e.g. Galbraith and Laslett, 1993; Vermeesch, 2018b). However, in this paper we will assume that such overdispersion is absent from the reference materials and from the single-spot analyses.

8 Dead-time correction

It takes a few tens of nanoseconds for a secondary electron multiplier to record the arrival of an ion. During this “dead time”, the detector is unable to register the arrival of additional ions. This phenomenon can significantly bias isotope ratio estimates that include ion beams of contrasting intensity. Fortunately, the dead-time effect can be easily corrected. It suffices that the dwell times are adjusted by the cumulative amount of time that the detectors were incapacitated. Let $d_x^{\prime }$ be the “effective dwell time” of ion beam x:

$$\begin{array}{}\text{(13)}& d_x^{\prime }=d_x-n_x{\mathit{\delta }}_x,\end{array}$$

where δ_x is the (non-extended) dead time of the detector that measures x. Then the expected normalised beam counts can be re-defined as

$$\begin{array}{}\text{(14)}& {\mathit{\theta }}_x^{\prime }={\displaystyle \frac{{\mathit{\varphi }}_x{d}_x^{\prime }}{{\mathit{\varphi }}_b{d}_b^{\prime }+{\sum }_{y\in \mathbb{x}}{\mathit{\varphi }}_y{d}_y^{\prime }}}\end{array}$$

and the normalised beam intensities as

$$\begin{array}{}\text{(15)}& {\mathit{\varphi }}_x^{\prime }={\displaystyle \frac{{\mathit{\theta }}_x/d_x^{\prime }}{{\mathit{\theta }}_b/d_b^{\prime }+{\sum }_{y\in \mathbb{x}}{\mathit{\theta }}_y^{\prime }/d_y}}.\end{array}$$

The difference between this approach and existing SIMS data reduction approaches is that conventional data reduction algorithms apply the dead-time correction to the raw data before calculating isotopic data, whereas the new method applies the dead-time correction to ${\mathit{\theta }}_x^{\prime }$ and ${\mathit{\varphi }}_x^{\prime }$, which are unknown parameters that must be estimated from the data.

9 Within-spot drift correction

Thus far we have assumed that all ions are measured synchronously, which is the case in multicollector configurations. However, in single-collector experiments, the measurements are made asynchronously. This can cause biased results if the signals drift over time. In SHRIMP data processing, it is customary to correct this drift by normalising to a secondary beam monitor (SBM) signal², followed by double interpolation of numerator and denominator isotopes (Bodorkos et al., 2020; Dodson, 1978). A unified data reduction algorithm for SHRIMP and Cameca instruments requires a different approach, in which the time dependency of the signals is parameterised using a log-linear model. For Faraday detectors,

$$\begin{array}{}\text{(16)}& n_x^i=\mathrm{bkg}+\mathcal{N}\left(\exp [{\mathit{\alpha }}_x+{\mathit{\gamma }}_X{\mathit{\tau }}_x^i],{\mathit{\sigma }}^{\mathrm{2}}\right),\end{array}$$

where $n_x^i$ is the ion beam intensity of the ith integration for mass x of element X evaluated at time ${\mathit{\tau }}_x^i$, σ is the standard deviation of the normally distributed data scatter around the best fit line, and “bkg” is the background signal. This is usually a nominal value for Cameca instruments and an actual set of measurements ($n_b^i$) for SHRIMP data. Note that the intercept parameters (α_x) are ionic-mass-specific, whereas the slopes (γ_X) are element-specific. See the Appendix for an example. For SEM detectors, the scatter of the data around the log-linear fit is controlled by Poisson shot noise:

$$\begin{array}{}\text{(17)}& n_x^i\sim \mathrm{bkg}+\mathrm{Pois}\left(\exp [{\mathit{\alpha }}_x+{\mathit{\gamma }}_X{\mathit{\tau }}_x^i]d_x^{\prime }\right).\end{array}$$

The background-corrected signal ratio (evaluated at ${\mathit{\tau }}_x^i$) for two ion beams x and y of different elements X and Y can then be drift-corrected as follows:

$$\begin{array}{}\text{(18)}& {}^i{\mathit{\beta }}_x^y\equiv \ln \left({\displaystyle \frac{{\mathit{\varphi }}_y^i-{\mathit{\varphi }}_b^i}{{\mathit{\varphi }}_x^i-{\mathit{\varphi }}_b^i}}\right)+{\mathit{\gamma }}_Y\left({\mathit{\tau }}_x^i-{\mathit{\tau }}_y^i\right),\end{array}$$

where ${\mathit{\varphi }}_x^i$ and ${\mathit{\varphi }}_y^i$ are the dead-time-corrected normalised beam intensities for the ith integration of masses x and y, respectively, and ${\mathit{\varphi }}_b^i$ is the corresponding background value. See the Appendix for further details.

10 Fractionation

Mass spectrometer signals are recorded in volts (for Faraday detectors) or hertz (or secondary electron multipliers). The age equation, however, requires atomic ratios. In general, signal ratios do not equal atomic ratios because they are affected by two types of fractionation.

1. Mass-dependent fractionation. The Pb isotopes span a range of four mass units, with ²⁰⁸Pb being 2 % heavier than ²⁰⁴Pb. Both the production and detection efficiency of secondary ions vary with atomic mass, and significant errors can potentially occur if the resulting mass fractionation is uncorrected for. Mass fractionation can be quantified by comparing the measured signal ratios of a reference material with its known isotopic ratio. This is easy to do in a log-ratio context (Vermeesch, 2015).

2. Elemental fractionation. The fractionation between the Pb isotopes is caused by (slight) differences in their physical properties, i.e. their mass. As briefly mentioned in Sect. 4, much stronger fractionation effects tend to occur between the isotopes and Pb and U because they are not only physically but also chemically different. These chemical differences affect the complex processes that occur when the primary ion beam interacts with the target material (Williams, 1998).

In the context of SIMS U–Pb geochronology, mass-dependent fractionation is commonly ignored (but not always, e.g. Stern et al., 2009) because the most important isochemical ratio is that between ²⁰⁶Pb and ²⁰⁷Pb, which lie within 0.5 % mass units of each other. This is unresolvable given typical analytical uncertainties. The mass fractionation is greater for ²⁰⁴Pb, but so is its analytical uncertainty. Therefore, the atomic ²⁰⁴Pb $/$ ²⁰⁶Pb, ²⁰⁷Pb $/$ ²⁰⁶Pb, and ²⁰⁸Pb $/$ ²⁰⁶Pb ratios can be directly estimated from the (drift-corrected) ²⁰⁴Pb $/$ ²⁰⁶Pb, ²⁰⁷Pb $/$ ²⁰⁶Pb, and ²⁰⁸Pb $/$ ²⁰⁶Pb signal ratios. This is not the case for the ²⁰⁶Pb $/$ ²³⁸U and ²⁰⁸Pb $/$ ²³²Th ratios, which are affected by strong elemental fractionation effects. This fractionation expresses itself in two ways.

1. Within-spot fractionation
   

   Over the course of a SIMS spot analysis, the Pb $/$ U and Pb $/$ Th ratio changes as a function of time. This elemental fractionation can be modelled using a log-linear model that is similar to that used for the within-spot drift correction:

   $$\begin{array}{}\text{(19)}& {}^i{\mathit{\beta }}_x^y{=}^{\mathrm{0}}{\mathit{\beta }}_x^y+{\mathit{\gamma }}_X^Y{\mathit{\tau }}_x^i,\end{array}$$

   where ${}^{\mathrm{0}}{\mathit{\beta }}_x^y$ is the inferred log ratio of the background-corrected signals at “time zero”, which can be found using the method of maximum likelihood (see the Appendix). Note that ${\mathit{\gamma }}_X^Y=\mathrm{0}$ if X=Y, and, if the sensitivity drift of the data is smooth and closely follows the trends defined by Eqs. (16) and (17), then ${}^{\mathrm{0}}{\mathit{\beta }}_x^y\approx {\mathit{\alpha }}_y-{\mathit{\alpha }}_x$ and ${\mathit{\gamma }}_X^Y\approx {\mathit{\gamma }}_Y-{\mathit{\gamma }}_X$.

   Using Eq. (19), the isotopic log ratios can be interpolated (or extrapolated) to any point in time (τ):

   $$\begin{array}{}\text{(20)}& {}^{\mathit{\tau }}{\mathit{\beta }}_x^y{=}^{\mathrm{0}}{\mathit{\beta }}_x^y+{\mathit{\gamma }}_X^Y\mathit{\tau }.\end{array}$$

   The most precise values of ${}^{\mathit{\tau }}{\mathit{\beta }}_x^y$ are obtained when τ is chosen in the middle of the analytical sequence. These values can be used for subsequent calculations. Alternatively, we can also use the time-zero intercepts ${}^{\mathrm{0}}{\mathit{\beta }}_x^y$.

2. Between-spot fractionation
   

   The Pb $/$ U and Pb $/$ Th signal ratios may vary between adjacent spots on the same isotopically homogenous reference material. This fractionation obeys the power-law relationship given by Eq. (2). Expressing this formula in terms of corrected signal ratios gives

   $$\begin{array}{}\text{(21)}& \begin{array}{rl}& \ln \left[{\displaystyle \frac{({\mathit{\varphi }}_{\mathrm{6}}^{\prime }-{\mathit{\varphi }}_b^{\prime })-({\mathit{\varphi }}_{\mathrm{4}}^{\prime }-{\mathit{\varphi }}_b^{\prime })(\mathrm{6}/\mathrm{4}{)}_{\mathrm{c}}}{{\mathit{\varphi }}_u^{\prime }-{\mathit{\varphi }}_b^{\prime }}}\right]=\\ & A+B\ln \left[{\displaystyle \frac{{\mathit{\varphi }}_o^{\prime }-{\mathit{\varphi }}_b^{\prime }}{{\mathit{\varphi }}_u^{\prime }-{\mathit{\varphi }}_b^{\prime }}}\right],\end{array}\end{array}$$

   where $(\mathrm{6}/\mathrm{4}{)}_{\mathrm{c}}$ stands for the ²⁰⁶Pb $/$ ²⁰⁴Pb ratio of the common Pb (see the footnote of Sect. 4). Recasting Eq. (21) in terms of the interpolated log-ratio estimates gives

   $$\begin{array}{}\text{(22)}& \ln \left[\exp {(}^{\mathit{\tau }}{\mathit{\beta }}_{\mathrm{u}}^{\mathrm{6}})-\exp {(}^{\mathit{\tau }}{\mathit{\beta }}_{\mathrm{u}}^{\mathrm{4}})(\mathrm{6}/\mathrm{4}{)}_{\mathrm{c}}\right]=A+B{}^{\mathit{\tau }}{\mathit{\beta }}_{\mathrm{u}}^{\mathrm{o}},\end{array}$$

   where “o” stands for the uranium oxide (²³⁸U¹⁶O${}_{\mathrm{2}}^{+}$ or ²³⁸U¹⁶O⁺) and “u” stands for ²³⁸U⁺.

11 U–Pb age calculation

Having applied Eq. (22) to a reference material with a known atomic ²⁰⁶Pb $/$ ²³⁸U ratio ${\left[{}^{\mathrm{206}}\mathrm{Pb}/{}^{\mathrm{238}}\mathrm{U}\right]}_{\mathrm{a}}^{\mathrm{r}}$, the atomic ²⁰⁶Pb $/$ ²³⁸U ratio of the sample is given by

$$\begin{array}{}\text{(23)}& \ln {\left[{\displaystyle \frac{{}^{\mathrm{206}}\mathrm{Pb}}{{}^{\mathrm{238}}\mathrm{U}}}\right]}_{\mathrm{a}}^{\mathrm{s}}=\ln {\left[{\displaystyle \frac{{}^{\mathrm{206}}\mathrm{Pb}}{{}^{\mathrm{238}}\mathrm{U}}}\right]}_{\mathrm{a}}^{\mathrm{r}}{+}^{\mathit{\tau }}{\mathit{\beta }}_{\mathrm{u}}^{\mathrm{6}}\left(s\right)-A-B{}^{\mathit{\tau }}{\mathit{\beta }}_{\mathrm{u}}^{\mathrm{o}}\left(s\right),\end{array}$$

where ${}^{\mathit{\tau }}{\mathit{\beta }}_{\mathrm{u}}^{\mathrm{6}}\left(s\right)$ and ${}^{\mathit{\tau }}{\mathit{\beta }}_{\mathrm{u}}^{\mathrm{o}}\left(s\right)$ are the interpolated log-ratio estimates of the sample. The ²⁰⁶Pb $/$ ²³⁸U age is then obtained by plugging ${\left[{}^{\mathrm{206}}\mathrm{Pb}/{}^{\mathrm{238}}\mathrm{U}\right]}_{\mathrm{a}}^{\mathrm{s}}$ into the age equation. Uncertainties are obtained by standard error propagation (see the Appendix).

12 Examples

The following paragraphs will illustrate the SIMS U–Pb data reduction process using two datasets.

1. Dataset 1 was acquired by Yang Li at IGG-CAS Beijing using a Cameca 1280HR instrument with five SEMs and two Faraday detectors run in single-collector mode using an SEM for all mass stations. The dataset uses Temora2 zircon (416.8 ± 1.1 Ma, Black et al., 2004) as a reference material and 91500 zircon (1062.4 ± 0.2 Ma, Wiedenbeck et al., 1995) as a sample. Measurements consist of seven cycles through a set of 11 mass stations per single-spot measurement for ⁹⁰Zr₂O (0.48 s dwell time per cycle), ⁹²Zr₂O (0.08 s), mass 200.5 (background, 4.00 s), ⁹⁴Zr₂O (0.32 s), ²⁰⁴Pb (4.96 s), ²⁰⁶Pb (2.96 s), ²⁰⁷Pb (6.00 s), ²⁰⁸Pb (2.00 s), ²³⁸U (2.96 s), ThO₂ (2.96 s), and UO₂ (2.96 s).

2. Dataset 2 was acquired by Simon Bodorkos at Geoscience Australia using a single-collector SHRIMP-II instrument, employing an SEM for all mass stations. This dataset also uses Temora2 as a reference material, as well as 91500 zircon, OG.1 (3440.7 ± 3.2 Ma, Stern et al., 2009), and M127 (524.36 ± 0.16 Ma, Nasdala et al., 2016) as samples. Measurements consist of six cycles through a set of 10 mass stations per single-spot measurement for ⁹⁰Zr₂O (2.0 s dwell time per cycle), ²⁰⁴Pb (20 s), mass 204.04091 (background, 20 s), ²⁰⁶Pb (15 s), ²⁰⁷Pb (40 s), ²⁰⁸Pb (5 s), ²³⁸U (5 s), ThO (2 s), UO (2 s), and UO₂ (2 s).

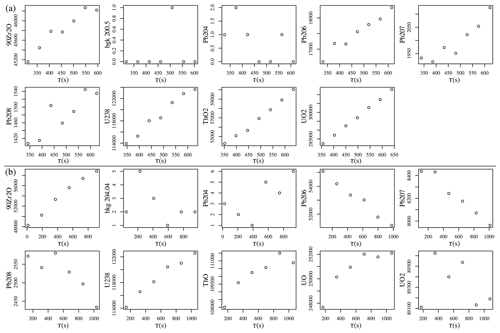
Figure 3 Time-resolved signals (counts) of (a) Temora2 (spot Tem@6) analysed by a Cameca 1280HR instrument at IGG-CAS Beijing; (b) M127 zircon (spot M127.1.2) analysed by a SHRIMP-II instrument at Geoscience Australia.

Figure 3 shows the time-resolved SEM counts of one representative spot measurement for each dataset. Side-by-side comparison of these two datasets reveals some interesting similarities and differences. All of the high-intensity signals exhibit clear transient behaviour, which is caused by changes in oxygen availability that occur during primary ion bombardment (Magee et al., 2017). The transience of the individual SEM signals biases the isotopic ratios. For example, there are 109 s between the ²⁰⁴Pb and ²⁰⁸Pb measurements in each SHRIMP cycle. During these 109 s, the ²⁰⁸Pb signal drops on average by 2 %, resulting in an equivalent bias of the ²⁰⁴Pb $/$ ²⁰⁸Pb ratio (Sect. 9). A similar drop per cycle is observed for the Cameca data.

However, there is a key difference between the Cameca and SHRIMP datasets. For the Cameca data, the U and Pb signals both drift in the same direction, resulting in positive slopes for the example of Fig. 3. But for the SHRIMP data, the U and Pb drift in opposite directions: the U signal exhibits an increase in sensitivity with time, whereas the Pb signals decrease in intensity with time. This marked difference in behaviour between the two instruments reflects a difference in their design, causing a difference in the energy window of the secondary ions analysed (Ireland and Williams, 2003).

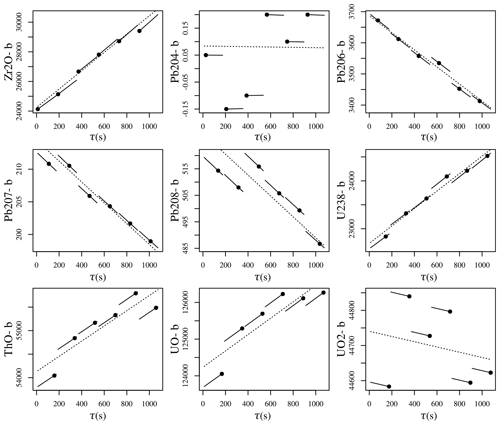
Figure 4 Within-spot drift correction of the background-corrected SHRIMP data from Fig. 3. Dotted lines are log-linear functions whose element-specific slopes (γ_X in Eq. 17) are used for the drift correction but for no other purpose. Solid lines mark the duration of each mass spectrometer cycle, with the black dots representing the starting point of each individual mass station within the cycles. The solid lines are parallel to the dotted lines (in log space) and express how the isotope ratio fits can be translated to match the asynchronous mass spectrometer signals. Vertical axes have units of counts per second.

For Faraday detectors, the within-spot drift correction uses a generalised linear model with a lognormal link function (Eq. 16). For SEM data, it uses a Poisson link function (Eq. 17). In either case, the model enforces strictly positive isotopic abundances. Isotopes of the same element (such as ${}^{\mathrm{204}\left|\mathrm{6}\right|\mathrm{7}|\mathrm{8}}$Pb) have the same slope parameter but different intercepts. Isotopes of different elements are free to have different slopes (Fig. 4).

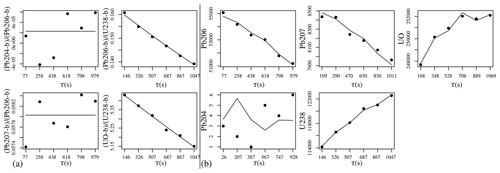
Figure 5 (a) Background- and drift-corrected ratio fits to the SHRIMP data from Fig. 3, obtained using the generalised linear model of Eq. (19). The slope parameter (${\mathit{\gamma }}_X^Y$ in Eq. 19) is zero for isotopes of the same element and non-zero for isotopes of different elements. Vertical axes are unitless. (b) The four (log-)ratio fits can be converted back to five isotope signal fits using the inverse log-ratio transformation. Multiplying the normalised ion beam intensity fits with the total number of counts per sweep allows direct comparison with the raw measurements, which are shown as filled circles. Vertical axes have units of counts. Note that the measurements have Poisson uncertainties, which scale with the square root of the values.

Figure 5 applies another log-linear function (Eq. 19) to model the within-spot fractionation of SHRIMP Temora2 spot 11. This function models the drift-corrected log ratios as a linear function of analysis time. The slopes of the log-linear functions are a function of the within-spot fractionation between the numerator and denominator elements. Because there is no fractionation between two isotopes of the same element, the slope of the Pb $/$ Pb ratios is zero.

The ability of log-ratio statistics to avoid negative ratios is apparent from the first panel of Fig. 5. Even though some of the the background-corrected ratio signals are zero or negative (because the background exceeded the signal), the generalised linear fit is strictly positive. The natural ability of compositional data analysis to rule out negative ratios avoids many problems further down the data processing chain.

The right-hand side of Fig. 5 maps the four (log) ratios back to five equivalent raw signals (one for each isotope). The last two panels of the figure show how the log-ratio approach manages to effectively capture subtle fluctuations of the U and UO signal intensities.

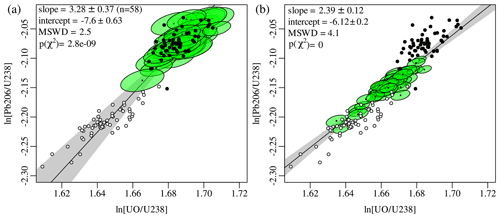
Figure 6 (a) U–Pb calibration curve for the Temora2 SHRIMP data using the time-zero (τ=0) intercepts (green ellipses). Black and white dots mark the first and last cycles of each analysis, respectively. (b) The log-ratio data and calibration fit for the same data, but evaluated at the midpoint (τ=544), resulting in a more precise calibration. All uncertainties are shown at 95 % confidence.

The log-ratio intercepts obtained by Eq. (19) form a linear array of calibration data (Eq. 22). Figure 6a fits a straight line through these points using the linear regression algorithm of York et al. (2004). Alternatively, instead of fitting a calibration line through the log-ratio intercepts (τ=0, Fig. 6a), it is also possible to interpolate or extrapolate the log-ratio composition to any other point in time. For example, the green ellipses in Fig. 6b show the inferred log-ratio compositions at 544 s (i.e. τ=544), which represents the midpoint of the analyses. The slope of this calibration line is notably different than that obtained by fitting a line through the compositions at 0 s. This change in slope reflects the different mechanisms that are responsible for elemental fractionation within and between SIMS spots.

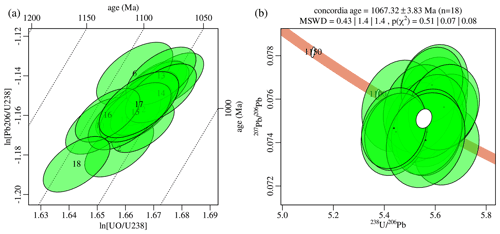
Figure 7 (a) Calibration plot of the SHRIMP 91500 zircon data using Temora2 as a reference material. Dotted lines are parallel to the regression line of Fig. 6b. (b) The same data shown on a Tera–Wasserburg concordia diagram, which was obtained with IsoplotR and does not take into account systematic errors associated with the calibration fit. All uncertainties are shown at 95 % confidence. The white ellipse marks the weighted mean composition, with MSWD and p values representing the goodness of fit for equivalence, concordance, and equivalence+concordance.

Table 2 Uncertainty budget of the four Temora2 zircon analyses highlighted in Fig. 8. The first two data columns show the calibrated ²⁰⁶Pb $/$ ²³⁸U log ratios and their standard errors ignoring the uncertainty of the calibration fit (i.e. using internal uncertainties only). The third column shows the total error including the external uncertainty associated with the calibration fit. The upper triangular matrix shown in the remaining three columns contains the (total) error correlations of the four aliquots.

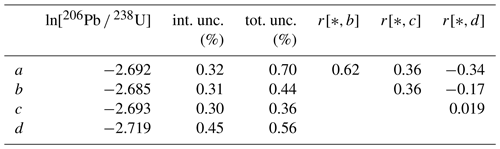
Figure 7 applies the Pb $/$ U calibration (Eq. 23) to 91500 zircon using the Temora2 data for calibration. It shows only the purely random errors, i.e. ignoring the uncertainty of the calibration. Including the calibration errors not only inflates the uncertainties, but also causes inter-spot error correlations (Fig. 1). To demonstrate this phenomenon, let us revisit the Cameca data and swap the sample and reference materials around. Thus, we use 91500 for the calibration curve and Temora2 as a sample (Fig. 8). Table 2 shows the uncertainty budget of four selected aliquots from this sample.

Figure 8 Calibration curve of the Cameca data using 91500 zircon as a reference material (top half of the plot) and Temora2 zircon as a sample (bottom half). a–d mark four Temora2 aliquots whose uncertainty budget is explored in Table 2.

Propagating the calibration curve uncertainty increases the error estimates (Table 2) by different amounts for different spots. For aliquot c, which is located immediately below the mean of the 91500 data, the calibration uncertainty only mildly increases the standard error from 0.30 % to 0.36 %. However, for aliquot a, which is horizontally offset from the mean of the calibration data, the systematic calibration uncertainty more than doubles the standard error from 0.32 % to 0.70 %. The calibration error also causes the standard errors of the various aliquots to be correlated with each other. For example, the total uncertainties of aliquots a and b are positively correlated ($r[a,b]=\mathrm{0.62}$) because their UO₂ $/$ U ratios are both offset from the mean of the calibration in the same direction. In contrast, the uncertainties of aliquots a and d are negatively correlated ($r[a,d]=-\mathrm{0.34}$) because they are offset in opposite directions from the mean of the calibration data.

The inter-spot error correlations are important when calculating weighted means (Vermeesch, 2015) and isochrons. Taking into account the full covariance structure of the data affects both the accuracy and the precision of any derived age information. For example, the conventional weighted mean can be replaced with a matrix expression that accounts for correlated uncertainties (Eq. 92 of Vermeesch, 2015). Applying this modified algorithm to the positively correlated aliquots a and b of Table 2 changes the weighted mean from −2.6922 to −2.6854 and increases the standard error of that mean from 0.37 % to 0.44 %. Applying the same calculation to the negatively correlated aliquots a and d changes their weighted mean from −2.7083 to −2.7076 and reduces uncertainty from 0.43 % to 0.35 %. To take full advantage of the covariance matrix will require the development of a new generation of high-level data reduction software. For example, future versions of IsoplotR (Vermeesch, 2018a) will be modified to handle these rich data structures. A comprehensive discussion of this topic falls outside the scope of this paper.

13 The R package simplex

The SIMS data processing algorithm presented in this paper is implemented in an R package called simplex. The programme can be run in three modes: online, offline, and from the command line. The online version can be accessed at https://isoplotr.es.ucl.ac.uk/simplex/ (last access: 16 August 2022). It contains three example U–Pb datasets, including the two datasets used in this paper, plus a Cameca monazite U–Th–Pb dataset.

The simplex package currently accepts raw data as Cameca .asc and SHRIMP .op and .pd files. Support for SHRIMP .xml files will be added later. The online version is a good place to try the look and feel of the software. However, it is probably not the most practical way to process lots of large data files. For a more responsive user experience, simplex can also be run natively on any operating system (Windows, Mac OS, or Linux). To this end, the user needs to install R on their system (see https://r-project.org/ for details, last access: 16 August 2022). Within R, the simplex package can be installed from the GitHub code-sharing platform using the remotes package by entering the following commands at the console.

install.packages("remotes")
remotes::install_github("pvermees/simplex")

Once installed, the simplex graphical user interface (GUI) can be started by entering the following command at the console.

simplex::simplex()

A third and final way to use simplex is from the command line. This allows advanced users to create automation scripts and extend the functionality of the package. The simplex package comes with an extensive API (Application Programming Interface) of fully documented user functions. An overview of all these functions can be obtained by typing the following command at the console.

help(package="simplex")

14 Discussion

This paper introduced a new algorithm for SIMS U–Pb geochronology, in which raw mass spectrometer signals are processed using a combination of log-ratio analysis and Poisson counting statistics. In contrast with existing data reduction protocols, which handle each aliquot of an analytical sequence separately, the new algorithm simultaneously processes all of them in parallel. It thereby produces an internally consistent set of isotopic ratios and their associated covariance matrix. This covariance matrix is a rich source of information that captures both random and systematic uncertainties, including inter-spot error correlations that have hitherto been ignored in geochronology.

The example data of Sect. 12 showed that these inter-spot error correlations can be either positive or negative (see also Vermeesch, 2015; McLean et al., 2016). Ignoring them affects both the accuracy and precision of high-end data processing steps such as isochron regression and concordia age calculation. Unfortunately, existing postprocessing software such as Isoplot (Ludwig, 2003) and IsoplotR (Vermeesch, 2018a) does not yet handle inter-spot error correlations. Further work is needed to extend these codes and take full advantage of the new algorithm. IsoplotR was designed with such future upgrades in mind: its input window contains a large number of spare columns that will accommodate covariance matrices in a future update. Once the aforementioned high-end data reduction calculations have been updated, it will be possible to fully quantify the gain in precision and accuracy of the new algorithm compared to the previous generation of SIMS data reduction software.

The data reduction principles laid out in this paper are applicable not only to U–Pb geochronology, but also to other SIMS applications such as stable isotope analysis. In fact, simplex already handles such data for multicollector Cameca instruments. It is worth mentioning that the stable isotope functionality can also be used to correct ²⁰⁷Pb $/$ ²⁰⁶Pb ratio measurements for mass-dependent isotope fractionation, as was briefly discussed in Sect. 10. Future updates of the mass-dependent fractionation correction will also address the overcounted background problem that was mentioned in Sect. 6.

Besides U–Pb geochronology and stable isotopes, the new data reduction paradigm can also be adapted to other chronometers and other mass spectrometer designs, such as thermal ionisation mass spectrometry (TIMS, Connelly et al., 2021), noble gas mass spectrometry (Vermeesch, 2015), and LAICPMS (McLean et al., 2016). The simplex package already includes a function to export data to IsoplotR. Adding similar functionality to other data processing software will improve geochronologists' ability to integrate multiple datasets whilst keeping track of systematic uncertainties, including those associated with reference materials and decay constants.

Appendix A

This section provides further algorithmic details for the new U–Pb data processing workflow. It assumes that ions are recorded on SEM detectors, which is by far the most common configuration. The case of Faraday collectors is similar and, in fact, simpler.

Within-spot drift is modelled using a log-linear function (Eq. 17) with a distinct intercept (α_x) for each ion channel (x) and shared slopes (γ_X) between isotopes of the same element (X). To illustrate this concept, consider the case of ${}^{\mathrm{204}\left|\mathrm{6}\right|\mathrm{7}}$Pb (inclusion of ²⁰⁸Pb is a trivial extension). Let ${\widehat{n}}_x^i$ be the time-dependent parameter of the shot noise for ^20xPb, where $x\in \mathit{\{}\mathrm{4},\mathrm{6},\mathrm{7}\mathit{\}}$:

$$\begin{array}{}\text{(A1)}& {\widehat{n}}_x^i=\mathrm{bkg}+\exp ({\mathit{\alpha }}_x+{\mathit{\gamma }}_{\mathrm{Pb}}{t}_x^i)d_x^{\prime }.\end{array}$$

Then the log-likelihood function of the parameters given the data is defined as

$$\begin{array}{}\text{(A2)}& \begin{array}{rl}& \mathcal{L}{\mathcal{L}}_d\left({\mathit{\alpha }}_{\mathit{\left\{}x\mathit{\right\}}},{\mathit{\gamma }}_{\mathrm{Pb}}|n_{\mathbb{x}}^i\right)=\\ & \mathrm{Const}.+\sum _x\sum _{i=\mathrm{1}}^N\left(n_x^i\ln \left[{\widehat{n}}_x^i\right]-{\widehat{n}}_x^i\right),\end{array}\end{array}$$

where N represents the number of cycles. The parameters ${\mathit{\alpha }}_{\mathit{\left\{}x\mathit{\right\}}}=\mathit{\{}{\mathit{\alpha }}_{\mathrm{4}},{\mathit{\alpha }}_{\mathrm{6}},{\mathit{\alpha }}_{\mathrm{7}}\mathit{\}}$ and γ_Pb are estimated by maximising ℒℒ_d with respect to them. Only γ_Pb is used in subsequent calculations. The intercepts α_{x} are discarded.

The next step of the data reduction extracts log ratios from the raw data using a log-linear model that is similar to the within-spot drift correction (Eq. 19). Here, in contrast with the drift correction, the intercepts are just as important as the slopes. For isochemical ratios such as ²⁰⁷Pb $/$ ²⁰⁶Pb, the slope of the drift-corrected log ratios is zero and we only need to estimate the intercept. For multichemical ratios such as ²³⁸U $/$ ²⁰⁶Pb, both the slope and the intercept are non-zero. In order to keep track of covariances, it is useful to process all the isotopes together using a common denominator. For example, using ²⁰⁶Pb (6) as a common denominator and ²⁰⁴Pb (4), ²⁰⁷Pb (7), ²³⁸U (u), and UO (o) as numerators,

$$\begin{array}{}\text{(A3)}& {}^i{\mathit{\beta }}_{\mathrm{6}}^x{=}^{\mathrm{0}}{\mathit{\beta }}_{\mathrm{6}}^x+{\mathit{\gamma }}_{\mathrm{6}}^x{\mathit{\tau }}_{\mathrm{6}}^i+{\mathit{\gamma }}_X\left({\mathit{\tau }}_x^i-{\mathit{\tau }}_{\mathrm{6}}^i\right)+\ln \left[d_{\mathrm{6}}^{\prime }\right]-\ln \left[d_x^{\prime }\right],\end{array}$$

where X stands for Pb if $x\in \mathit{\{}\mathrm{4},\mathrm{6},\mathrm{7}\mathit{\}}$, for U if x=u, and for UO if x=o. Then the normalised ion counts are given by

$${\mathit{\theta }}_y^i=\exp \left[{}^i{\mathit{\beta }}_{\mathrm{6}}^y\right]/D_i$$

and

$$\begin{array}{}\text{(A4)}& {\mathit{\theta }}_{\mathrm{6}}^i=\mathrm{1}/D_i\end{array}$$

for $y\in \mathit{\{}\mathrm{4},\mathrm{7},u,o\mathit{\}}$, with

$$\begin{array}{}\text{(A5)}& D_i=\mathrm{1}+\sum _y\exp \left[{}^i{\mathit{\beta }}_{\mathrm{6}}^y\right]+{\displaystyle \frac{n_b^i}{{\sum }_z{n}_z^i}},\end{array}$$

in which $z\in \mathit{\{}\mathrm{4},\mathrm{6},\mathrm{7},u,o,b\mathit{\}}$. Then the log-likelihood is calculated as

$$\begin{array}{}\text{(A6)}& \mathcal{L}{\mathcal{L}}_l\left({}^{\mathrm{0}}{\mathit{\beta }}_{\mathrm{6}}^{\mathit{\left\{}x\mathit{\right\}}},{\mathit{\gamma }}_{\mathrm{6}}^{\mathit{\left\{}x\mathit{\right\}}}|n_{\mathbb{x}}^i\right)=\mathrm{Const}.+\sum _{i=\mathrm{1}}^N\sum _x{n}_x^i\ln \left[{\mathit{\theta }}_x^i\right],\end{array}$$

where ${\mathit{\gamma }}_{\mathrm{6}}^{\mathrm{4}}={\mathit{\gamma }}_{\mathrm{6}}^{\mathrm{7}}=\mathrm{0}$ because there is no elemental fractionation between the Pb isotopes. From the log ratios with a common denominator, it is easy to derive any other log ratio:

$$\begin{array}{}\text{(A7)}& {}^{\mathit{\tau }}{\mathit{\beta }}_x^y{=}^{\mathit{\tau }}{\mathit{\beta }}_{\mathrm{6}}^y{-}^{\mathit{\tau }}{\mathit{\beta }}_{\mathrm{6}}^x.\end{array}$$

One of the main advantages of the new data reduction method is its ability to keep track of the full covariance structure of the data, including inter-spot error correlations. This ability is derived from the fact that all parameters are derived by the method of maximum likelihood, which stipulates that the approximate covariance matrix of any set of estimated parameters can be obtained by inverting the negative matrix of second derivatives (i.e. the Hessian matrix) of the log-likelihood function with respect to said parameters.

$$\begin{array}{}\text{(A8)}& \mathbf{\Sigma }\approx -{\mathcal{H}}^{-\mathrm{1}}\end{array}$$

For example, to estimate the covariance matrix of the log-ratio slopes and intercepts for a single-spot analysis, the Hessian is a 6×6 matrix that includes the second derivatives of ℒℒ_l with respect to ${\mathit{\beta }}_{\mathrm{6}}^{\mathrm{4}}$, ${\mathit{\beta }}_{\mathrm{6}}^{\mathrm{7}}$, ${\mathit{\beta }}_{\mathrm{6}}^{\mathrm{u}}$, ${\mathit{\beta }}_{\mathrm{6}}^{\mathrm{o}}$, ${\mathit{\gamma }}_{\mathrm{6}}^{\mathrm{u}}$, and ${\mathit{\gamma }}_{\mathrm{6}}^{\mathrm{o}}$. Computing this matrix is tedious to do by hand but straightforward to do numerically.

Given the covariance matrix of the log ratios, subsequent data reduction steps propagate the analytical uncertainties by a conventional first-order Taylor approximation. Thus, if y=f(x), then

$$\begin{array}{}\text{(A9)}& {\mathbf{\Sigma }}_y\approx {\mathbf{J}}_f{\mathbf{\Sigma }}_x{\mathbf{J}}_f^{\mathrm{T}},\end{array}$$

where J_f is the Jacobian matrix (and ${\mathbf{J}}_f^{\mathrm{T}}$ its transpose) of partial derivatives of f with respect to x. For example, to estimate the m×m covariance matrix of m fractionation-corrected ²⁰⁶Pb $/$ ²³⁸U ratios, error propagation of Eq. (23) would involve an $m\times (\mathrm{2}m+\mathrm{3})$ Jacobian matrix and a $(\mathrm{2}m+\mathrm{3})\times (\mathrm{2}m+\mathrm{3})$ covariance matrix containing the uncertainties of A, B, and $\ln {\left[\frac{{}^{\mathrm{206}}\mathrm{Pb}}{{}^{\mathrm{238}}\mathrm{U}}\right]}_{\mathrm{a}}^{\mathrm{r}}$, as well as ${}^{\mathit{\tau }}{\mathit{\beta }}_u^{\mathrm{6}}\left(j\right)$ and ${}^{\mathit{\tau }}{\mathit{\beta }}_u^o\left(j\right)$ (for j from 1 to m).