Errorchrons and anchored isochrons in IsoplotR

Isochrons are usually fitted by “York regression”, which uses a weighted least-squares approach that accounts for correlated uncertainties in both variables. Despite its tremendous popularity in modern geochronology, the York algorithm has two important limitations that reduce its utility in several applications. First, it does not provide a satisfactory mechanism to deal with so-called “errorchrons”, i.e. datasets that are overdispersed with respect to the analytical uncertainties. Second, York regression is not readily amenable to anchoring, in which either the slope or the intercept of the isochron is fixed based on some external information. Anchored isochrons can be very useful in cases where the data are insufficiently spread out to constrain both the radiogenic and non-radiogenic isotopic composition.

This paper addresses both of these issues by extending a maximum likelihood algorithm that was first proposed by Titterington and Halliday (1979). The new algorithm offers the ability to attribute any excess dispersion to either the inherited component (“model 3a”) or diachronous closure of the isotopic system (“model 3b”). It provides an opportunity to anchor isochrons to either a fixed non-radiogenic composition or a fixed age. Last but not least, it allows the user to attach meaningful analytical uncertainty to the anchor. The new method has been implemented in IsoplotR for immediate use in $\mathrm{Ar}/\mathrm{Ar}$, $\mathrm{Pb}/\mathrm{Pb}$, $\mathrm{U}/\mathrm{Pb}$, $\mathrm{Th}/\mathrm{Pb}$, $\mathrm{Rb}/\mathrm{Sr}$, $\mathrm{Sm}/\mathrm{Nd}$, $\mathrm{Lu}/\mathrm{Hf}$, $\mathrm{Re}/\mathrm{Os}$, $\mathrm{K}/\mathrm{Ca}$, and U–Th–He geochronology.

1 Introduction

Isochrons are mixing lines between radiogenic and inherited isotopic endmembers. They are an essential component of radiometric geochronology and exist in several forms. Sections 1–7 of this paper will deal with the simple case of “$P/D$ isochrons”, which apply to geochronometers that are based on the decay of a single radioactive parent nuclide (P; e.g. ⁸⁷Rb, ⁴⁰K, ¹⁴⁷Sm) to a particular daughter nuclide (D; e.g. ⁸⁷Sr, ⁴⁰Ar, ¹⁴³Nd). Sections 8 and 9 will discuss $\mathrm{Pb}/\mathrm{Pb}$ and $\mathrm{U}/\mathrm{Pb}$ isochrons, respectively. These are based on the paired decay of two parents (²³⁸U and ²³⁵U) to two daughters (²⁰⁶Pb and ²⁰⁷Pb, respectively) and require linear regression in two or three dimensions.

$P/D$ isochrons come as two types. “Conventional” isochrons are straight-line relationships of the following kind:

$$\begin{array}{}\text{(1)}& {\left[{\displaystyle \frac{D}{d}}\right]}_i={\left[{\displaystyle \frac{D}{d}}\right]}_{\mathrm{0}}+{\left[{\displaystyle \frac{P}{d}}\right]}_i\left(e^{\mathit{\lambda }t}-\mathrm{1}\right),\end{array}$$

where i is the aliquot number ($\mathrm{1}\le i\le n$), d is a non-radiogenic sister isotope of D, $[D/d{]}_{\mathrm{0}}$ is the inherited component, λ is the decay constant, and t is the time elapsed since isotopic closure. A full list of definitions is provided in Appendix A. “Inverse” isochrons are obtained by permuting P, D, and d:

$$\begin{array}{}\text{(2)}& {\left[{\displaystyle \frac{d}{D}}\right]}_i={\left[{\displaystyle \frac{d}{D}}\right]}_{\mathrm{0}}\left\{\mathrm{1}-{\left[{\displaystyle \frac{P}{D}}\right]}_i\left(e^{\mathit{\lambda }t}-\mathrm{1}\right)\right\}.\end{array}$$

The choice between conventional and inverse isochrons depends on the relative precision of the mass spectrometer measurements. Inverse isochrons are preferred if d≪D. Otherwise, conventional isochrons are fine (Li and Vermeesch, 2021).

Equations (1) and (2) can be recast into a generic linear form:

$$\begin{array}{}\text{(3)}& y_i=a+b{x}_i.\end{array}$$

Table A1 maps the parameters of this generic equation to the parameters of Eqs. (1) and (2) as well as subsequent variants thereof. Equation (3) is usually solved by York et al. (2004) regression (hereafter simply referred to as “York regression”). York regression uses a least-squares algorithm to estimate the intercept (a) and slope (b) of the isochron line from an n×5 table of paired isotopic ratio measurements, along with their standard errors and their error correlations.

Although this paper will use the York parameters a and b to fit the isochron, all results will be presented in terms of the geologically more meaningful inherited endmember ratio $[D/d{]}_{\mathrm{0}}$ and radiogenic endmember ratio $[D/P{]}^{\ast }\equiv e^{\mathit{\lambda }t}-\mathrm{1}$, where $[D/d{]}_{\mathrm{0}}=a$ and $[D/P{]}^{\ast }=b$ for conventional isochrons and $[D/d{]}_{\mathrm{0}}=\mathrm{1}/a$ and $[D/P{]}^{\ast }=-b/a$ for inverse isochrons (Li and Vermeesch, 2021).

The most accurate and precise results are obtained from samples that are evenly spread along the isochron line, spanning the entire range of values from the inherited to the radiogenic endmember. Unfortunately, this condition is not always fulfilled. It is not uncommon for most or all aliquots in a sample to cluster together at one point along the isochron, making it difficult to accurately estimate the endmember compositions. For example, no precise isochron ages can be obtained from samples whose radiogenic daughter component is dwarfed by the inherited daughter component. Conversely, the composition of the inherited component cannot be precisely estimated in extremely radiogenic samples. Finally, when the data cluster together in the middle, then neither endmember component can be reliably determined (Fig. 1).

Sometimes, such poorly constrained isochrons can be fixed using external information. For example, if the composition of the inherited component is known through some independent means (e.g. by analysing a cogenetic mineral that is naturally poor in P and rich in D and d), then this information can be used to anchor the isochron. Anchoring reduces the number of unknown parameters by 1, benefitting numerical stability and precision. Conversely, if the age of the sample is known, then the inherited component can be estimated by anchoring to the radiogenic endmember.

There is currently no formally documented way to anchor York regression. A commonly used “hack” is to add an extra data point with infinite precision representing either the inherited or radiogenic endmember component. However, this hack does not provide a satisfactory mechanism to assign uncertainty to the anchor. This paper solves that problem. Section 2 introduces a maximum likelihood formulation of York regression, which is amenable to anchoring with uncertainty. Section 3 shows how this formulation can be used to model “errorchrons” that are overdispersed with respect to the analytical uncertainties.

Section 4 provides further details about the implementation of maximum likelihood regression, which can attribute overdispersion to either the intercept (“model 3a”) or slope (“model 3b”) of the linear fit. It turns out that model 3b is computationally more challenging than model 3a. Section 5 shows how this issue can be avoided by inverting and flipping the isochron axes.

Section 6 shows how anchored isochron regression represents a trivial special case of the maximum likelihood algorithm. Section 7 attaches two different geological interpretations to the uncertainty of isochron anchors. These two interpretations lead to two different fit models (“model 1” and “model 3”, which are so named for historical reasons). Sections 8 and 9 apply the same logic to $\mathrm{Pb}/\mathrm{Pb}$ and $\mathrm{U}/\mathrm{Pb}$ isochrons, respectively. Finally, Sect. 10 shows how the new algorithms can be used within the IsoplotR software package.

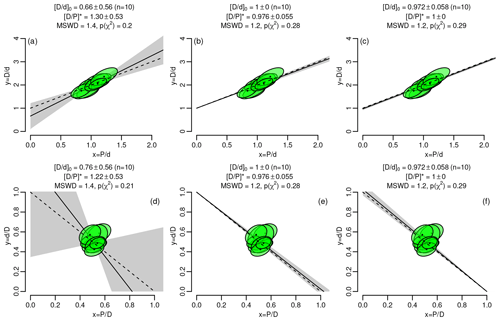
Figure 1 $P/D$ isochron diagrams for a synthetic dataset generated using the procedures of Appendix B. The true slope and intercept are a=1 and b=1 for the conventional isochrons (a–c) and a=1 and $b=-\mathrm{1}$ for the inverse isochrons (d–f). These parameter values correspond to $[D/d{]}_{\mathrm{0}}=[D/P{]}^{\ast }=\mathrm{1}$. The true trends are shown as dashed lines and the estimated trends as solid lines, with 95 % confidence envelopes shown in grey. The estimated parameter values are shown above the panels. Unconstrained isochron regression (a, d) yields imprecise and inaccurate results. Fixing the inherited component (b, e) or the radiogenic component (c, f) greatly improves both aspects of the fit.

2 Maximum likelihood formulation of York regression

York et al. (2004) use the method of least squares to fit the general problem of weighted regression with correlated uncertainties in both variables. Titterington and Halliday (1979) obtained identical results using the method of maximum likelihood. The latter approach offers greater flexibility than least squares and will be used in the remainder of this paper.

The method of maximum likelihood is a standard statistical technique to estimate the parameters of a probability distribution from a set of measurements. In the case of two-dimensional isochron regression, the parameters are the intercept a, the slope b, and the true (but unknown) x_i values. The data are the X_i and Y_i measurements along with their assumed uncertainties and error correlations (see Appendix A for a full list of definitions). For a dataset of n aliquots, there are 2n measurements (n X_i values and n Y_i values) and n+2 parameters (a, b, and n x_i values). That leaves $\mathrm{2}n-n-\mathrm{2}=n-\mathrm{2}$ “degrees of freedom” to estimate the parameters.

This overconstrained problem can be solved by minimizing the paired differences (“residuals”) between the true x_i and y_i values (where $y_i=a+b{x}_i$) and between the measured X_i and Y_i values.

$$\begin{array}{}\text{(4)}& \left\{\begin{array}{l}{X}_i=x_i+{\mathit{ϵ}}_{x,i}\\ Y_i=a+b{x}_i+{\mathit{ϵ}}_{y,i}\end{array}\right.\end{array}$$

To make the problem tractable, the vector of residuals Δ_i is assumed to be drawn from a bivariate normal distribution with zero mean and covariance matrix Σ_i:

$${\mathbf{\Delta }}_i\equiv \left[\begin{array}{l}{X}_i-x_i\\ Y_i-y_i\end{array}\right]=\left[\begin{array}{l}{\mathit{ϵ}}_{x,i}\\ {\mathit{ϵ}}_{y,i}\end{array}\right]$$

and

$$\begin{array}{}\text{(5)}& {\mathbf{\Sigma }}_i\equiv \left[\begin{array}{ll}s[X_i{]}^{\mathrm{2}}& s[X_i,Y_i]\\ s[X_i,Y_i]& s[Y_i{]}^{\mathrm{2}}\end{array}\right].\end{array}$$

The product of the normal probabilities for all the aliquots (from $\mathrm{1}\le i\le n$) is called the “likelihood” of the parameters given the data. Maximizing this number produces the most accurate possible parameter estimates $\widehat{a}$, $\widehat{b}$, and ${\widehat{x}}_i$. Alternatively, and equivalently, the same estimates can be obtained by maximizing the logarithm of the likelihood. This is the preferred approach as it improves numerical stability and facilitates the estimation of the parameter uncertainties. The log-likelihood function can be formally defined as

$$\begin{array}{}\text{(6)}& -\mathcal{L}\mathcal{L}\left(\text{parameters}\right|\text{data})=n\ln (\mathrm{2}\mathit{\pi })+{\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}\sum _{i=\mathrm{1}}^n\left(\ln \left|{\mathbf{\Sigma }}_i\right|+{\mathbf{\Delta }}_i^T{\mathbf{\Sigma }}_i^{-\mathrm{1}}{\mathbf{\Delta }}_i\right).\end{array}$$

This formulation allows for correlated uncertainties between the variables ($s[X_i,Y_i]\ne \mathrm{0}$ in Eq. 5) but not between aliquots ($s[X_i,Y_j]=\mathrm{0}$ if i≠j). Daëron and Vermeesch (2023) discuss the generalized case of “omnivariant” regression, where this requirement has been relaxed and Eq. (6) is replaced with a single matrix expression.

3 Dealing with overdispersion

The degree to which the residuals Δ_i are consistent with the assumed analytical uncertainties Σ_i can be assessed using a chi-square test and the MSWD parameter. Readers who are not familiar with these concepts are referred to Appendix C for details. Isochrons that exhibit significant overdispersion with respect to the analytical uncertainties are colloquially referred to as errorchrons. Whether it is right to use such a pejorative term for this common phenomenon is debatable (Schaen et al., 2021). Four approaches may be used to deal with errorchrons.

Model 1.

Inflate the analytical uncertainties by a factor $\sqrt{\text{MSWD}}$.

Model 2.

Ignore the analytical uncertainties and replace York regression with orthogonal regression or a similar technique. This approach will not be discussed further in this paper.

Model 3.

Quantify the dispersion as an additional free parameter. There are two options for doing so.

•  

  Model 3a. Attribute the excess dispersion to variability of the inherited component and, hence, the isochron intercept. For conventional isochrons, this means that the true isotopic ratios of the cogenetic aliquots do not belong to a single isochron line but to a family of parallel isochron lines whose intercepts are normally distributed (Titterington and Halliday, 1979). The standard deviation of this normal distribution (σ_a) can be used to quantify the dispersion of the data around the “central” isochron line.

•  

  Model 3b. Attribute the excess dispersion to diachronous closure of the isotopic system. This mechanism produces families of conventional isochrons that share a common intercept but differ in their slopes. Again, the distribution of the slopes can be assumed to follow a normal distribution, with mean b and standard deviation σ_b. The latter value can be used to quantify the dispersion of the data, which in this case captures the degree of diachroneity.

Model 3a isochron regression can be formalized by modifying Eq. (4) as follows:

$$\begin{array}{}\text{(7)}& \left\{\begin{array}{l}{X}_i=x_i+{\mathit{ϵ}}_{x,i}\\ Y_i=a+b{x}_i+{\mathit{ϵ}}_a+{\mathit{ϵ}}_{y,i}.\end{array}\right.\end{array}$$

The dispersion parameter σ_a can be estimated (as ${\widehat{\mathit{\sigma }}}_a$) by incorporating it into the covariance matrices:

$$\begin{array}{}\text{(8)}& {\mathbf{\Sigma }}_{a,i}\equiv \left[\begin{array}{ll}s[X_i{]}^{\mathrm{2}}& s[X_i,Y_i]\\ s[X_i,Y_i]& s[Y_i{]}^{\mathrm{2}}+{\mathit{\sigma }}_a^{\mathrm{2}}\end{array}\right].\end{array}$$

The equivalent expressions for model 3b regression are

$$\begin{array}{}\text{(9)}& \left\{\begin{array}{l}{X}_i=x_i+{\mathit{ϵ}}_{x,i}\\ Y_i=a+(b+{\mathit{ϵ}}_b)x_i+{\mathit{ϵ}}_{y,i}\end{array}\right.\end{array}$$

and

$$\begin{array}{}\text{(10)}& {\mathbf{\Sigma }}_{b,i}\equiv \left[\begin{array}{ll}s[X_i{]}^{\mathrm{2}}& s[X_i,Y_i]\\ s[X_i,Y_i]& s[Y_i{]}^{\mathrm{2}}+(x_i{\mathit{\sigma }}_b{)}^{\mathrm{2}}\end{array}\right],\end{array}$$

respectively.

4 Specific cases

Three specific cases of Eq. (6) are of interest in the present discussion.

Model 1.

$$\begin{array}{}\text{(11)}& \mathcal{L}{\mathcal{L}}_{\mathrm{1}}(a,b,\mathbf{x}|\mathbf{X},\mathbf{Y},\mathbf{\Sigma })=\text{constant}-{\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}\sum _{i=\mathrm{1}}^n{\mathbf{\Delta }}_i^T{\mathbf{\Sigma }}_i^{-\mathrm{1}}{\mathbf{\Delta }}_i\end{array}$$

Model 3a.

$$\begin{array}{}\text{(12)}& \begin{array}{rl}& \mathcal{L}{\mathcal{L}}_{\mathrm{3}a}(a,b,{\mathit{\sigma }}_a,\mathbf{x}|\mathbf{X},\mathbf{Y},\mathbf{\Sigma })=\\ & \text{constant}-{\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}\sum _{i=\mathrm{1}}^n\left(\ln \left|{\mathbf{\Sigma }}_{a,i}\right|+{\mathbf{\Delta }}_i^T{\mathbf{\Sigma }}_{a,i}^{-\mathrm{1}}{\mathbf{\Delta }}_i\right)\end{array}\end{array}$$

Model 3b.

$$\begin{array}{}\text{(13)}& \begin{array}{rl}& \mathcal{L}{\mathcal{L}}_{\mathrm{3}b}(a,b,{\mathit{\sigma }}_b,\mathbf{x}|\mathbf{X},\mathbf{Y},\mathbf{\Sigma })=\\ & \text{constant}-{\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}\sum _{i=\mathrm{1}}^n\left(\ln \left|{\mathbf{\Sigma }}_{b,i}\right|+{\mathbf{\Delta }}_i^T{\mathbf{\Sigma }}_{b,i}^{-\mathrm{1}}{\mathbf{\Delta }}_i\right)\end{array}\end{array}$$

Note that the (logged) determinant of the covariance matrices is not included in the constant for model 3 fits because Σ_a,i and Σ_b,i are both functions of x, whereas Σ_i is not. ℒℒ can be numerically maximized using an iterative two-step procedure. For model 1 regression, the first step maximizes $\mathcal{L}{\mathcal{L}}_{\mathrm{1}}\left(\mathbf{x}\right|a,b,\mathbf{X},\mathbf{Y},\mathbf{\Sigma })$ to find x for any pair of a and b values. The second step repeats the first step for different values of a and b until the overall optimum is reached.

This procedure can easily be adapted to model 3 regression by adding σ_a or σ_b to the unknown parameters. It works well for model 3a, where the first step has a direct solution. However, it is slow for model 3b regression, in which finding x requires an additional level of iteration. See Appendix D for further details. Fortunately, in practice model 3b is rarely or never needed for geochronology, as explained next.

5 Flipped isochron regression

For inverse isochrons, model 3b regression does not actually provide any useful information. Unlike conventional isochrons, whose chronological information is contained in the slope, the chronological information of inverse isochrons is contained in their horizontal intercept. This information can be unlocked by flipping the axes of the isochron diagram around, inverting the isochron, and treating the $D/P$ ratio as the dependent variable. Applying model 3a regression to the flipped data yields a dispersion estimate σ_a that can be used to quantify the age dispersion.

The same trick can be used to estimate the slope uncertainty of a conventional isochron. A pragmatic way to avoid the slow convergence rate of model 3b regression is to invert the isochron, flip the dependent and independent variables around, invert the isochron a second time, and carry out a model 3a regression on the transformed data. The resulting σ_a estimate can be converted to a σ_b estimate:

$$\begin{array}{}\text{(14)}& {\widehat{\mathit{\sigma }}}_b\left(\text{conventional isochron}\right)\approx {\displaystyle \frac{{\widehat{\mathit{\sigma }}}_a}{{\widehat{a}}^{\mathrm{2}}}}\left(\text{flipped inverse isochron}\right).\end{array}$$

Figure 2 applies model 3 regression to two synthetic Ar–Ar datasets with a non-radiogenic ${}^{\mathrm{40}}\mathrm{Ar}{/}^{\mathrm{36}}\mathrm{Ar}$ ratio of 400 and an age of 100 Ma. The dataset of Fig. 2a exhibits overdispersion of the y intercept ([⁴⁰Ar $/$ ³⁶Ar${]}_{\mathrm{0}}=\mathrm{400},{\mathit{\sigma }}_a=\mathrm{40}$), whereas the dataset of Fig. 2b is overdispersed in the x intercept (t=100 Ma, σ_t=10 Ma). In both cases, the maximum likelihood algorithm has retrieved the correct solution from the noisy data.

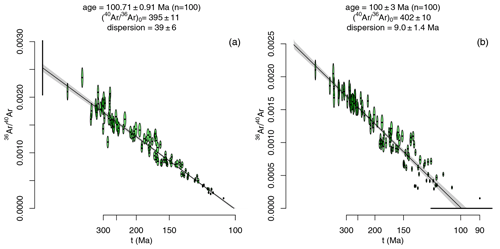
Figure 2 Model 3 regression of two synthetic Ar–Ar datasets. (a) Model 3a regression through 100 randomly drawn aliquots from an isochron with a true non-radiogenic ${}^{\mathrm{40}}\mathrm{Ar}{/}^{\mathrm{39}}\mathrm{Ar}$ ratio of 400±40 (1σ) and a true age of 100 Ma; (b) model 3b regression through 100 aliquots from an isochron with a true non-radiogenic ${}^{\mathrm{40}}\mathrm{Ar}{/}^{\mathrm{39}}\mathrm{Ar}$ ratio of 400 and a true age of 100±10 Ma (1σ). Error bars on the y and x axis show the overdispersion at 95 % confidence.

6 Anchored isochron regression

Anchored isochron regression requires just a trivial modification of the maximum likelihood algorithm. It suffices to treat the anchored parameter as data. For example, the slope and intercept of a model 1 isochron can be anchored by maximizing $\mathcal{L}{\mathcal{L}}_{\mathrm{1}}(a,\mathbf{x}|b,\mathbf{X},\mathbf{Y},\mathbf{\Sigma })$ and $\mathcal{L}{\mathcal{L}}_{\mathrm{1}}(b,\mathbf{x}|a,\mathbf{X},\mathbf{Y},\mathbf{\Sigma })$, respectively. Note that these calculations assume that the anchor is known exactly. This is reflected in the zero uncertainties of the non-radiogenic component in Fig. 1b and e and of the radiogenic components in Fig. 1c and f. Such absolute certainty is unrealistic in the noisy world of geology. Section 7 introduces two ways to formally account for uncertainty in anchored isochron regression.

7 Accounting for anchor uncertainty

When assigning uncertainty to statistical parameters, it is important to clearly define the meaning of this uncertainty. In the case of anchored isochron regression, the uncertainty of the intercept or slope can carry two meanings. For example, when the intercept of an isochron is anchored at a value $\overline{a}\pm {\mathit{\sigma }}_{\overline{a}}$, this can mean either of the following.

Model 1.

The data are underlain by a single isochron whose intercept is only approximately known, with a most likely value of $\overline{a}$ and a precision (standard error) of ${\mathit{\sigma }}_{\overline{a}}$.

Model 3.

The data were drawn from a family of isochron lines whose intercepts follow a normal distribution with mean $\overline{a}$ and standard deviation ${\mathit{\sigma }}_{\overline{a}}$.

These two different approaches can be implemented by replacing the log-likelihood functions of Eq. (13) with the following.

$$\begin{array}{}\text{(15)}& \begin{array}{l}\mathbf{\text{Model 1}}.\\ \mathcal{L}{\mathcal{L}}_{\mathrm{1}}(a,b,\mathbf{x}|\overline{a},{\mathit{\sigma }}_{\overline{a}},\mathbf{X},\mathbf{Y},\mathbf{\Sigma })=\\ \text{constant}+\mathcal{L}{\mathcal{L}}_{\mathrm{1}}(a,b,\mathbf{x}|\mathbf{X},\mathbf{Y},\mathbf{\Sigma })-\frac{\mathrm{1}}{\mathrm{2}}{\left(\frac{a-\overline{a}}{{\mathit{\sigma }}_{\overline{a}}}\right)}^{\mathrm{2}}\\ \mathbf{\text{Model 3}}.\\ \mathcal{L}{\mathcal{L}}_{\mathrm{3}a}(b,\mathbf{x}|\overline{a},{\mathit{\sigma }}_{\overline{a}},\mathbf{X},\mathbf{Y},\mathbf{\Sigma })\end{array}\end{array}$$

The equivalent expressions for anchored slopes with uncertainty are as follows.

$$\begin{array}{}\text{(16)}& \begin{array}{l}\mathbf{\text{Model 1}}.\\ \mathcal{L}{\mathcal{L}}_{\mathrm{1}}(a,b,\mathbf{x}|\overline{b},{\mathit{\sigma }}_{\overline{b}},\mathbf{X},\mathbf{Y},\mathbf{\Sigma })=\\ \text{constant}+\mathcal{L}{\mathcal{L}}_{\mathrm{1}}(a,b,\mathbf{x}|\mathbf{X},\mathbf{Y},\mathbf{\Sigma })-\frac{\mathrm{1}}{\mathrm{2}}{\left(\frac{b-\overline{b}}{{\mathit{\sigma }}_{\overline{b}}}\right)}^{\mathrm{2}}\\ \mathbf{\text{Model 3}}.\\ \mathcal{L}{\mathcal{L}}_{\mathrm{3}b}(a,\mathbf{x}|\overline{b},{\mathit{\sigma }}_{\overline{b}},\mathbf{X},\mathbf{Y},\mathbf{\Sigma })\end{array}\end{array}$$

Note that model 1 treats the slope and intercept as unknowns, so their maximum likelihood estimates generally do not equal the anchored values $\overline{a}$ and $\overline{b}$. However, the smaller ${\mathit{\sigma }}_{\overline{a}}$ and ${\mathit{\sigma }}_{\overline{b}}$ are relative to $\overline{a}$ and $\overline{b}$, the closer that $\widehat{a}$ and $\widehat{b}$ are to $\overline{a}$ and $\overline{b}$. In contrast, anchored model 3 regression fixes the dispersion of the anchored parameters so that ${\widehat{\mathit{\sigma }}}_a={\mathit{\sigma }}_{\overline{a}}$ for anchored intercepts, whereas ${\widehat{\mathit{\sigma }}}_b={\mathit{\sigma }}_{\overline{b}}$ for anchored slopes.

Figure 3 applies the two approaches to the synthetic dataset of Fig. 1 using anchors of $[D/d{]}_{\mathrm{0}}=\mathrm{1}\pm \mathrm{0.05}$ and $[D/P{]}^{\ast }=\mathrm{1}\pm \mathrm{0.05}$ (1σ). As expected, models 1 and 3 produce slightly different outcomes, with model 1 resulting in $[D/d{]}_{\mathrm{0}}$ and $[D/P{]}^{\ast }$ estimates that are slightly different than the anchored values, whereas model 3 reproduces the anchors exactly. The model 3 fits produce more precise estimates for the unanchored quantities. This reflects the fact that some of the uncertainty in the isochron is captured by the dispersion parameter, which is absent from the model 1 fit.

Model 3 partitions the analytical and geological uncertainty between the standard errors of $\widehat{a}$ and $\widehat{b}$ on the one hand and the dispersion parameter on the other hand. It is not easy to visualize this partitioned uncertainty. Figure 3 uses a grey confidence envelope to show the analytical uncertainty and a black error bar to visualize the geological dispersion. Together these two items represent the total uncertainty budget.

It is, of course, also possible to treat the dispersion parameter as an unknown by maximizing $\mathcal{L}{\mathcal{L}}_{\mathrm{3}a}(b,{\mathit{\sigma }}_a,\mathbf{x}|\overline{a},\mathbf{X},\mathbf{Y},\mathbf{\Sigma })$ or $\mathcal{L}{\mathcal{L}}_{\mathrm{3}b}(a,{\mathit{\sigma }}_b,\mathbf{x}|\overline{b},\mathbf{X},\mathbf{Y},\mathbf{\Sigma })$. Section 9 will give an example of this in the context of U–Pb geochronology.

Figure 3 Anchored isochrons for the data of Fig. 1, shown on inverse isochrons. Panels (a) and (b) anchor the non-radiogenic endmember composition to $[D/d{]}_{\mathrm{0}}=\mathrm{1}\pm \mathrm{0.05}$ (1σ). Panels (c) and (d) anchor the radiogenic endmember composition to $[D/P{]}^{\ast }=\mathrm{1}\pm \mathrm{0.05}$ (1σ). Panels (a) and (c) use model 1 isochron regression, whereas panels (b) and (d) use model 3. Note how the estimated values for $[D/d{]}_{\mathrm{0}}$ and $[D/P{]}^{\ast }$ are exactly the same as the anchored values for model 3 but not for model 1. The vertical error bar in panel (b) and the horizontal error bar in panel (d) represent the fixed dispersion of the vertical and horizontal intercept, respectively.

8 $\mathrm{Pb}/\mathrm{Pb}$ isochrons

The ${}^{\mathrm{207}}\mathrm{Pb}{/}^{\mathrm{206}}\mathrm{Pb}$ method is based on the paired decay of two radioactive parents P₁ and P₂ (²³⁸U and ²³⁵U) to two daughters D₁ and D₂ (²⁰⁶Pb and ²⁰⁷Pb, respectively) in the presence of a non-radiogenic sister isotope d (²⁰⁴Pb). This gives rise to the following implicit age equation:

$$\begin{array}{}\text{(17)}& {\displaystyle \frac{[D_{\mathrm{2}}/d{]}_i-[D_{\mathrm{2}}/d{]}_{\mathrm{0}}}{[D_{\mathrm{1}}/d{]}_i-[D_{\mathrm{1}}/d{]}_{\mathrm{0}}}}=\left[{\displaystyle \frac{P_{\mathrm{2}}}{P_{\mathrm{1}}}}\right]{\displaystyle \frac{e^{{\mathit{\lambda }}_{\mathrm{2}}t}-\mathrm{1}}{e^{{\mathit{\lambda }}_{\mathrm{1}}t}-\mathrm{1}}},\end{array}$$

where λ₁ and λ₂ are the decay constants of P₁ and P₂, respectively, and $[P_{\mathrm{2}}/P_{\mathrm{1}}]$ is constant. Equation (17) can be recast into the generic form of Eq. (3) to form a “$D/D$ isochron” using the mapping of Table A1. This gives rise to conventional (${}^{\mathrm{207}}\mathrm{Pb}{/}^{\mathrm{204}}\mathrm{Pb}$ vs. ${}^{\mathrm{206}}\mathrm{Pb}{/}^{\mathrm{204}}\mathrm{Pb}$) and inverse (${}^{\mathrm{207}}\mathrm{Pb}{/}^{\mathrm{206}}\mathrm{Pb}$ vs. ${}^{\mathrm{204}}\mathrm{Pb}{/}^{\mathrm{206}}\mathrm{Pb}$) isochrons.

Unlike inverse $P/D$ isochrons, which are characterized by negative slopes, inverse $D/D$ isochrons have positive slopes. There is perfect symmetry between conventional and inverse $D/D$ isochrons in the sense that the intercept of a conventional isochron equals the slope of an inverse isochron and vice versa. This slightly changes and, in fact, simplifies the procedure for anchored isochron regression.

There is no need for flipped isochron regression of $\mathrm{Pb}/\mathrm{Pb}$ data. Instead, all possible scenarios can be handled by straightforward model 1 and model 3a regression. Isochrons can be anchored to the non-radiogenic component in conventional isochron space and to the radiogenic component in inverse isochron space.

9 $\mathrm{U}/\mathrm{Pb}$ isochrons

The $\mathrm{U}/\mathrm{Pb}$ method, like the $\mathrm{Pb}/\mathrm{Pb}$ method, is based on the paired decay of ²³⁸U to ²⁰⁶Pb and of ²³⁵U to ²⁰⁷Pb. The two chronometers can be treated separately and plotted as $P/D$ isochrons. These two-dimensional isochrons can be anchored to the radiogenic and non-radiogenic composition using the methods described in Sects. 2–7.

$$\begin{array}{}\text{(18)}& \left\{\begin{array}{l}{\left[\frac{{}^{\mathrm{206}}\text{Pb}}{{}^{\mathrm{204}}\text{Pb}}\right]}_i={\left[\frac{{}^{\mathrm{206}}\text{Pb}}{{}^{\mathrm{204}}\text{Pb}}\right]}_{\mathrm{0}}+{\left[\frac{{}^{\mathrm{238}}\text{U}}{{}^{\mathrm{204}}\text{Pb}}\right]}_i\left(e^{{\mathit{\lambda }}_{\mathrm{238}}t}-\mathrm{1}\right)\\ {\left[\frac{{}^{\mathrm{207}}\text{Pb}}{{}^{\mathrm{204}}\text{Pb}}\right]}_i={\left[\frac{{}^{\mathrm{207}}\text{Pb}}{{}^{\mathrm{204}}\text{Pb}}\right]}_{\mathrm{0}}+{\left[\frac{{}^{\mathrm{235}}\text{U}}{{}^{\mathrm{204}}\text{Pb}}\right]}_i\left(e^{{\mathit{\lambda }}_{\mathrm{235}}t}-\mathrm{1}\right)\end{array}\right.\end{array}$$

Alternatively, the two ingrowth equations can also be coupled, forming a three-dimensional “total $\mathrm{Pb}/\mathrm{U}$ isochron”. This problem can be solved using the method of maximum likelihood (Ludwig, 1998). There is just one important difference between this solution and the York-like algorithm of Sect. 2. York regression is formulated in terms of a generic intercept (a) and slope (b). In contrast, the “Ludwig” algorithm is formulated in terms of the actual non-radiogenic ${}^{\mathrm{206}}\mathrm{Pb}{/}^{\mathrm{204}}\mathrm{Pb}$ (=α) and ${}^{\mathrm{207}}\mathrm{Pb}{/}^{\mathrm{204}}\mathrm{Pb}$ (=β) ratio, as well as the age (t) of the system.

It is relatively straightforward to generalize the concept of model 3 regression to total $\mathrm{Pb}/\mathrm{U}$ isochrons when the dispersion is attributed to the isochron age. However, it is not immediately clear how to do the same for the non-radiogenic composition because this would require partitioning the dispersion between the α and β parameters. This paper will not attempt to answer this question. Instead, let us conclude the technical discussion by shifting to a far more common type of $\mathrm{U}/\mathrm{Pb}$ data.

Most published $\mathrm{U}/\mathrm{Pb}$ studies do not report ²⁰⁴Pb because this nuclide is rare and difficult to measure. Instead, “semitotal $\mathrm{Pb}/\mathrm{U}$” regression is done in Wetherill or Tera–Wasserburg concordia space, which are akin to conventional and inverse isochron space, respectively. In the absence of a non-radiogenic sister isotope of Pb, the isochron is then redefined as a mixing line between an inherited ${}^{\mathrm{207}}\mathrm{Pb}{/}^{\mathrm{206}}\mathrm{Pb}$ ratio and the radiogenic ${}^{\mathrm{206}}\mathrm{Pb}{/}^{\mathrm{238}}\mathrm{U}$ and ${}^{\mathrm{207}}\mathrm{Pb}{/}^{\mathrm{235}}\mathrm{U}$ ratios.

The semitotal $\mathrm{Pb}/\mathrm{U}$ problem can be cast into a maximum likelihood format by replacing Eq. (4) with

$$\begin{array}{}\text{(19)}& \left\{\begin{array}{l}{X}_i=x_i+e^{{\mathit{\lambda }}_{\mathrm{235}}t}-\mathrm{1}+{\mathit{ϵ}}_{x,i}\\ Y_i=a+b{x}_i+{\mathit{ϵ}}_{y,i},\end{array}\right.\end{array}$$

where X_i and Y_i are the measured ${}^{\mathrm{207}}\mathrm{Pb}{/}^{\mathrm{235}}\mathrm{U}$ and ${}^{\mathrm{206}}\mathrm{Pb}{/}^{\mathrm{238}}\mathrm{U}$ ratios of the ith aliquot, respectively, and x_i is the true ${}^{\mathrm{207}}{\mathrm{Pb}}_{\mathrm{0}}{/}^{\mathrm{235}}\mathrm{U}$ ratio of the ith aliquot, whilst $a=e^{{\mathit{\lambda }}_{\mathrm{238}}t}-\mathrm{1}$ and $b={[}^{\mathrm{206}}\text{Pb}{/}^{\mathrm{207}}\text{Pb}{]}_{\mathrm{0}}{[}^{\mathrm{235}}\text{U}{/}^{\mathrm{238}}\text{U}]$. Equation (19) can be solved using the same recipe as the York reformulation of Sects. 2–7, with the caveat that the isochron terminates on the concordia line at the $\mathrm{U}/\mathrm{Pb}$ composition corresponding to t.

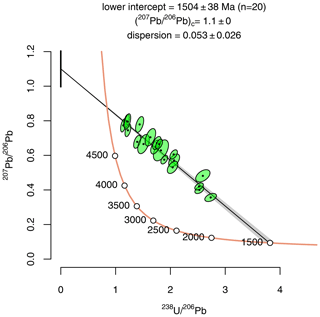
Figure 4 shows a model 3a anchored semitotal $\mathrm{Pb}/\mathrm{U}$ isochron in Tera–Wasserburg space. The true age for this synthetic dataset is 1500 Ma. The unconstrained model 1 isochron produces an imprecise isochron age of 1491±100 Ma, which is improved to 1504±38 Ma by anchoring to ${[}^{\mathrm{207}}\text{Pb}{/}^{\mathrm{206}}\text{Pb}{]}_{\mathrm{0}}=\mathrm{1.1}$. Just like the $P/D$ isochrons of Fig. 3, the uncertainty budget for the $\mathrm{U}/\mathrm{Pb}$ isochrons of Fig. 4 is partitioned between the analytical and geological dispersion, where the latter is treated as a free parameter with a maximum likelihood estimate of ${\widehat{\mathit{\sigma }}}_a=\mathrm{0.053}\pm \mathrm{0.026}$.

Figure 4 Model 3a semitotal $\mathrm{Pb}/\mathrm{U}$ isochron for a synthetic dataset with a true age t=1500 Ma, anchored to ${}^{\mathrm{207}}\mathrm{Pb}{/}^{\mathrm{206}}\mathrm{Pb}=\mathrm{1.10}$ with the dispersion parameter treated as a free parameter.

10 Implementation in IsoplotR

All the algorithms presented in this paper have been implemented in the free and open geochronological toolbox IsoplotR (Vermeesch, 2018). The ability to fit isochrons with models 1, 2, and 3 dates back to IsoplotR's first public release. Versions 2.1 and 5.2 added model 1 anchors to $\mathrm{U}/\mathrm{Pb}$ isochrons without and with uncertainty, respectively. Anchored York regression and model 3 anchors with uncertainty were added to IsoplotR 6.0. These functions can be accessed via the GUI or from the command line.

In the GUI, anchored regression is available from the “isochron” menu (so not from the “concordia” menu for $\mathrm{U}/\mathrm{Pb}$ data). The relevant settings can be selected from the “options” menu and should be self-explanatory. Moving on to the R console, use a built-in ${}^{\mathrm{40}}\mathrm{Ar}{/}^{\mathrm{39}}\mathrm{Ar}$ dataset to illustrate the command-line functionality and start with an unanchored inverse isochron fit using York regression.

library(IsoplotR)
attach(examples)
isochron(ArAr)

Carry out model 3a isochron regression anchored to a variable initial ${}^{\mathrm{40}}\mathrm{Ar}{/}^{\mathrm{36}}\mathrm{Ar}$ ratio of 300±5 (1σ).

settings('iratio','Ar40Ar36',300,5)
isochron(ArAr,anchor=1,model=3,taxis=TRUE)

Here, settings(…) is used to change the non-radiogenic argon composition, anchor=1 fixes the isochron to the inherited component, model=3 tells IsoplotR to assign the dispersion to the reported uncertainty of the atmospheric ${}^{\mathrm{40}}\mathrm{Ar}{/}^{\mathrm{36}}\mathrm{Ar}$ ratio, and taxis=TRUE changes the x axis to a timescale (as in Fig. 2).

Finally, carry out model 3b isochron regression anchored to a radiogenic composition that was set at 62±1 Ma (1σ).

isochron(ArAr,anchor=c(2,62,1),
         model=3,taxis=TRUE)

The dispersion can be changed to a free parameter by setting the third element of the anchor argument to a non-positive value. Documentation for additional options and settings can be accessed from the console using the help(isochron) or ?isochron commands.

11 Conclusions

This paper builds on previous work by McIntyre et al. (1966), Titterington and Halliday (1979), and Ludwig (2012). McIntyre et al. (1966) introduced the concept of model 3 isochron regression, attributing the excess dispersion of errorchrons to variability of the inherited component. This approach is implemented in Isoplot (Ludwig, 2012) and is referred to as model 3a regression in this paper. Note that the McIntyre et al. (1966) definition of model 2 regression differs from that of Ludwig (2012). It is more akin (but not identical) to the $\sqrt{\text{MSWD}}$ approach of Sect. 3.

Titterington and Halliday (1979) recast the model 3 algorithm of McIntyre et al. (1966) in a maximum likelihood framework. This paper extends the maximum likelihood approach to a second type of geological scenario, in which excess dispersion of the data around the isochron is not attributed to the inherited component but to the radiogenic component. This approach is referred to as model 3b regression.

The maximum likelihood formulation of isochron regression can also be used to anchor isochrons to either the inherited or the radiogenic component and to assign geologically meaningful uncertainty to the anchor. In reality it is possible that some samples are affected by both mechanisms so that different aliquots of the same sample differ in their initial ratios as well as the timing of their isotopic closure. Unfortunately, it is not possible to simultaneously capture both types of dispersion using the algorithms of this paper.

The difference between model 1 and model 3 regression represents two contrasting views of geological reality. The model 1 approach assumes that the isotopic composition of minerals represents discrete components recorded at distinct events. In contrast, model 3 isochrons represent a “fuzzier” reality, in which the initial composition or timing of isotopic closure is allowed to vary within a rock. Under the latter model, the concept of an errorchron no longer makes sense.

Appendix A: Definitions

P	a radioactive parent (e.g. 87Rb)
D	the radiogenic daughter of P (e.g. 87Sr)
d	a non-radiogenic sister isotope of D (e.g. 86Sr)
a, b, xi, yi	the true (but unknown) values of the intercept, slope, and isotopic ratio of the ith aliquot (out of n aliquots) from a sample
$\widehat{a}$, $\widehat{b}$, ${\widehat{x}}_i$, ${\widehat{y}}_i$	the estimated values of a, b, xi, and yi, respectively
Xi, Yi	the measured values of xi and yi, respectively
s[Xi], s[Yi], s[Xi,Yi]	the standard errors and covariance of Xi and Yi
${\mathit{ϵ}}_{x,i}=X_i-x_i$, ${\mathit{ϵ}}_{y,i}=Y_i-y_i$	the residuals of the data around the best-fit line
Σi	the 2×2 covariance matrix of Xi and Yi
x, y, X, Y, Σ	arrays and sets containing all n xi, yi, Xi, Yi, and Σi values

All uncertainties in this paper are reported as 95 % confidence intervals except if noted otherwise.

Table A1 Assignment of the isotopic ratios for $P/D$ and $D/D$ isochrons to the generic parameters of Eq. (3).

Appendix B: Data

The synthetic data in Figs. 1 and 3 were generated as follows.

1. Generate x by drawing 10 random numbers from a logit-normal distribution where the mean and standard deviation of the logits are 0 and 1$/$5, respectively.

2. Generate y by plugging x into Eq. (3) with $a=b=\mathrm{1}$.

3. Turn the resulting 10 pairs of {x_i,y_i} values into 10 trios of $\mathit{\{}{P}_i,D_i,d_i\mathit{\}}$ values where d_i is a random number between 100 and 500.

4. Use each of the $\mathit{\{}{P}_i,D_i,d_i\mathit{\}}$ values obtained in the previous step as parameters for a Poisson experiment.

5. Use the Poisson values obtained in the previous step to form 10 pairs of X and Y measurements and their (correlated) uncertainties.

6. Add some excess dispersion by shrinking the uncertainties by 20 %.

Note that this procedure fits the definition of a model 1 isochron, even though panels (b) and (d) of Fig. 3 use the resulting data to illustrate model 3 regression. The synthetic data in Figs. 2 and 4 are generated using a slightly different algorithm that simulates model 3a and 3b overdispersion. This modified procedure uses steps 1 and 3–4 of the procedure for Fig. 1 whilst replacing step 2 with a random effects model, in which a and b are drawn from random normal distributions with standard deviations corresponding to the dispersion parameters ${\mathit{\sigma }}_{\overline{a}}$ (10 % for Fig. 2a and 5 % for Fig. 4) and ${\mathit{\sigma }}_{\overline{b}}$ (10 % for Fig. 2b).

Appendix C: Testing overdispersion

Whether a dataset is overdispersed with respect to the analytical uncertainties can be formally assessed using the chi-square statistic and test. To this end, calculate the χ² statistic using the sum of squares term of Eq. (6).

$$\begin{array}{}\text{(C1)}& {\mathit{\chi }}^{\mathrm{2}}=\sum _{i=\mathrm{1}}^n{\mathbf{\Delta }}_i^T{\mathbf{\Sigma }}_i^{-\mathrm{1}}{\mathbf{\Delta }}_i\end{array}$$

If analytical uncertainty is the only source of dispersion in the dataset, then χ² is expected to follow a chi-square distribution with n−2 degrees of freedom ($\text{DF}=n-\mathrm{2}$, or, for anchored regression, $\text{DF}=n-\mathrm{1}$). This is called the “null distribution”. The probability of observing a value greater than χ² under this distribution is called the p value. A p value cutoff of 0.05 is generally used to distinguish isochrons (p≥0.05) from errorchrons (p<0.05). Dividing Eq. (C1) by the number of degrees of freedom produces a “reduced chi-square statistic”, which is known to geologists as an MSWD (McIntyre et al., 1966).

$$\begin{array}{}\text{(C2)}& \text{MSWD}={\displaystyle \frac{{\mathit{\chi }}^{\mathrm{2}}}{\text{DF}}}\end{array}$$

In the absence of overdispersion and for sufficiently large samples (n>20), the expected null distribution of the MSWD is approximately normal with a mean of 1 and a standard deviation $\sqrt{\mathrm{2}/\text{DF}}$ (Wendt and Carl, 1991). This information can be used as an alternative way to test the null hypothesis.

Appendix D: Further details about the maximum likelihood solution

Section 4 describes how the log-likelihood functions of Eq. (13) can be maximized in a two-step process: (1) find the x_i values that maximize ℒℒ for any pair of a and b values, and (2) search the space of a and b values until the overall maximum is found. For model 1 regression, the first step has a direct solution. Some shorthand notation for the inverse of the covariance matrix Σ_i is introduced:

$$\begin{array}{}\text{(D1)}& {\mathbf{\Sigma }}_i^{-\mathrm{1}}\equiv \left[\begin{array}{ll}{\mathrm{\Omega }}_{\mathrm{1},\mathrm{1}}^i& {\mathrm{\Omega }}_{\mathrm{1},\mathrm{2}}^i\\ {\mathrm{\Omega }}_{\mathrm{2},\mathrm{1}}^i& {\mathrm{\Omega }}_{\mathrm{2},\mathrm{2}}^i\end{array}\right],\end{array}$$

where ${\mathrm{\Omega }}_{\mathrm{1},\mathrm{2}}={\mathrm{\Omega }}_{\mathrm{2},\mathrm{1}}$. The fitted points x_i can be found by solving

$$\begin{array}{}\text{(D2)}& {\left.{\displaystyle \frac{\partial \mathcal{L}{\mathcal{L}}_{\mathrm{1}}}{\partial x_i}}\right|}_{{\widehat{x}}_i}=\mathrm{0},\end{array}$$

which yields

$$\begin{array}{}\text{(D3)}& {\widehat{x}}_i={\displaystyle \frac{X_i({\mathrm{\Omega }}_{\mathrm{1},\mathrm{1}}^i+b{\mathrm{\Omega }}_{\mathrm{1},\mathrm{2}}^i)+(Y_i-a)({\mathrm{\Omega }}_{\mathrm{2},\mathrm{1}}^i+b{\mathrm{\Omega }}_{\mathrm{2},\mathrm{2}}^i)}{({\mathrm{\Omega }}_{\mathrm{1},\mathrm{1}}^i+b{\mathrm{\Omega }}_{\mathrm{1},\mathrm{2}}^i)+b({\mathrm{\Omega }}_{\mathrm{2},\mathrm{1}}^i+b{\mathrm{\Omega }}_{\mathrm{2},\mathrm{2}}^i)}}.\end{array}$$

The same approach can be used for model 3a regression (with $\partial \mathcal{L}{\mathcal{L}}_{\mathrm{3}a}/\partial x_i=\mathrm{0}$). However, it does not work for model 3b isochrons because ${\partial }^{\mathrm{2}}\mathcal{L}{\mathcal{L}}_{\mathrm{3}b}/\partial x_i\partial x_j\ne \mathrm{0}$ when i≠j. Therefore, the x_i values are interdependent and cannot be solved separately. Although it is possible to jointly optimize the entire x vector, this takes considerably longer than model 1 and model 3a regression. Fortunately, as explained in Sect. 5, model 3b regression can be reformulated in terms of the model 3a algorithm.