the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Interpreting cooling dates and histories from laser ablation in situ (U–Th–Sm) ∕ He thermochronometry: a modelling perspective
Christoph Glotzbach
Todd A. Ehlers
Recent applications of the in situ (U–Th–Sm) He thermochronometry technique demonstrate its potential to address some of the analytical challenges associated with the whole-grain technique. In this study, we adapted state-of-the-art apatite and zircon production–ejection–diffusion models for application to in situ dating methods, aiming to enhance the applicability of this technique to a broad range of geologic samples and applications. Our modifications to thermal history models include accommodation of the full range of stopping distances for alpha particles and cylindrical grain geometries. This investigation focuses on several key aspects of in situ data interpretation: (i) exploring the relationship between in situ dates and the position of ablation spots across individual grains, (ii) assessing differences and similarities between whole-grain and in situ dates, (iii) determining optimal strategies and performance for reconstructing cooling histories from in situ (U–Th–Sm) He data, and (iv) reporting the effects of radionuclide zoning on (U–Th–Sm) He thermochronology. Results indicate that the measured in situ helium distribution is a function of grain size, ablation spot position and size, and cooling history. Together, these analytical and natural factors result in systematic variations in in situ dates with distance from the grain rim. Therefore, similar to whole-grain analyses, robust interpretation requires determining grain geometry and the distance of the laser spot from the nearest prismatic face. In most cases, resulting in situ dates are approximately 30 % older than corresponding alpha-ejection-corrected whole-grain dates, irrespective of the cooling rate and grain size. Whole-grain and in situ dates are similar solely for gem-sized samples or samples exhibiting negligible diffusional helium loss and thus spent more time at surface temperatures compared to their transit time through the partial retention zone. Reconstruction of cooling histories using in situ (U–Th–Sm) He data can be achieved through single measurements in several grains with varying grain size and/or effective uranium content or within a single grain with measurements taken at different distances from the grain rim. In addition, statistical analysis of a large compilation of measured radionuclide variations in apatite and zircon grains reveals that radionuclide zoning strongly impacts whole-grain analyses but can be directly measured with the in situ method. Overall, our results suggest that in situ measurements for (U–Th–Sm) He date determination offer a means to extract meaningful cooling signals from samples with poor reproducibility from traditional whole-grain techniques.
- Article
(10705 KB) - Full-text XML
-
Supplement
(1320 KB) - BibTeX
- EndNote
Alpha decay of radioisotopes and related ingrowth of 4He in crystal grains is the basis of the widely applicable (U–Th–Sm) He method (e.g. Lippolt et al., 1994; Wolf et al., 1996; Farley, 2002). A wide variety of minerals incorporate trace amounts of naturally occurring alpha-emitting isotopes such as U, Th, and Sm. Among those minerals, apatite and zircon have some favourable properties, making them a common choice for a wide range of applications to problems in tectonics and surface processes (e.g. Farley, 2000, 2002; Gallagher et al., 1998; Reiners and Ehlers, 2005; Malusà and Fitzgerald, 2019). Most importantly, apatite and zircon are abundant in many rock types, have a well-defined He diffusion behaviour (e.g. Farley, 2000; Reiners, 2005; Hourigan et al., 2005; Flowers et al., 2009; Guenthner et al., 2013), and are sensitive to upper-crustal temperatures (e.g. Ehlers, 2005; Reiners and Brandon, 2006). Most applications of apatite and zircon (U–Th–Sm) He thermochronometry make use of this and invert (U–Th–Sm) He data to retrieve cooling histories of exhumed rocks (e.g. Wolf et al., 1996). The majority of (U–Th–Sm) He thermochronometry studies use multiple whole-grain measurements from a single sample, often in combination with other thermochronometric data (e.g. Flowers, 2009; Guenthner et al., 2017; Falkowski et al., 2023). This is possible because He diffusion in apatite and zircon is controlled by grain size and accumulated radiation damage, both of which vary from grain to grain and thus lead to sample- and thermal-history-specific relationships between these parameters. An alternative method to reveal the near-surface thermal history of rocks is the method (Shuster and Farley, 2004), which indirectly measures the He profile by stepwise degassing of He from proton-irradiated apatite grains.
Irrespective of the method applied, deriving accurate cooling histories is often difficult because of biases introduced by (i) fluid inclusion or inclusion of radionuclide-rich mineral phases (e.g. Farley, 2002; Ehlers and Farley, 2003; Vermeesch et al., 2007; Danišík et al., 2017), (ii) implantation of He from radionuclide-rich phases from outside the grain (Spiegel et al., 2009), and (iii) radionuclide zonation and related variability of diffusion caused by radiation damage (e.g. Hourigan et al., 2005; Fox et al., 2014; Anderson et al., 2017). Careful selection of euhedral grains free of visible inclusion can prevent large biases caused by the first process. In the case of detrital studies where understanding the date distribution is the objective, excluding grains can introduce bias in the resulting date distributions. The in situ (U–Th–Sm) He method theoretically provides less biased results since unsuitable parts of grains can be excluded from analyses (e.g. Tripathy-Lang et al., 2013). Radionuclide zoning and the implantation of He are usually not accounted for in common (U–Th–Sm) He protocols. Implanted radiation damage in apatite and zircon and zonation, especially in zircon, increase the variance in whole-grain (U–Th–Sm) He dates and are likely the main causes for over-dispersed dates (e.g. Flowers et al., 2009; Horne et al., 2016, 2019).
In this regard, the introduction of the in situ (U–Th–Sm) He method by Boyce et al. (2006) has the potential to resolve some of the issues related to whole-grain analyses. However, in situ dating has not become a routine alternative to whole-grain measurements, despite several studies demonstrating the reliability of dating large and/or rapidly cooled monazite, zircon, and apatite age standards (e.g. Boyce et al., 2006; Tripathy-Lang et al., 2013; Evans et al., 2015). One potential issue is the complex geometric relation between radionuclides and produced He, originating from long alpha-stopping distances (up to several tens of micrometres) and separation of decay product from sourced parental radionuclide (e.g. Farley et al., 1996). Another potential issue is that more common small grains with less rapid cooling suffer from partial He loss by diffusion and thus should result in younger whole-grain dates compared to in situ (U–Th–Sm) He dates (e.g. Tripathy-Lang et al., 2013). He loss by diffusion mainly occurs in the outer part of a grain (Fig. 1a). An in situ He measurement in the centre of a grain (Fig. 1b) results in a date that is similar to a whole-grain date only for cooling scenario 1 that involves rapid cooling to the surface, followed by a prolonged stay at the surface (Fig. 1c). In cooling scenarios 2 and 3 that involve a longer time at temperatures where He diffusion is occurring, in situ dates are older compared to whole-grain dates (Fig. 1c).
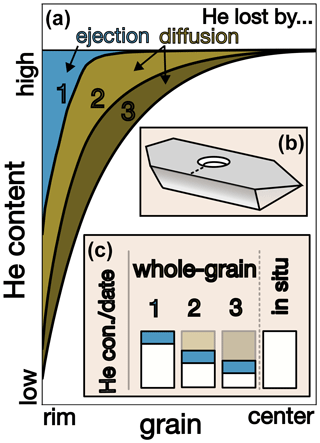
Figure 1Whole-grain vs. in situ (U–Th–Sm) He dates for end-member He profiles. (a) Modelled He profiles for three cooling histories assuming uniform radionuclide distributions: (1) rapid cooling to surface temperature, followed by a prolonged stay at the surface; (2) constant slow cooling; and (3) a prolonged stay in the partial retention zone, followed by rapid cooling to the surface. The blue area is the He content lost by alpha ejection, whereas He lost by diffusion is shown in brown. (b) Cylindrical grain with ablation pit and location of He profiles in (a). (c) Corresponding He concentrations and resulting whole-grain and in situ (U–Th–Sm) He dates for the cooling histories in (1), (2), and (3). Note that ejected He (blue bar) is added to the measured He (white bar) in the whole-grain approach based on grain geometry (Ft correction). The corresponding in situ dates calculated for a central pit are identical irrespective of cooling histories and are similar to the whole-grain date only for the rapid cooling scenario (1). In all other cases, He is lost by diffusion, especially in the outer part of grains, and in situ (U–Th–Sm) He dates are older compared to a whole-grain (U–Th–Sm) He dates.
In this study, we explore the theoretical measurement procedures required to interpret in situ (U–Th–Sm) He dates to retrieve cooling histories from multiple measurements in several grains or from a single grain. To do this, we simulate the He concentration across grains as a function of grain size and shape, radionuclide zoning, and cooling history. These predicted He distributions across grains are used to investigate the theoretical relationship between the size and position of in situ laser ablation spots and the corresponding in situ (U–Th–Sm) He dates. The in situ modelled dates are then compared to modelled whole-grain dates to identify the usability and limitations of each technique. In addition, the effect of radionuclide zoning in apatite and zircon on whole-grain dates is studied based on a large LA-ICP-MS (laser ablation inductively coupled plasma mass spectrometry) dataset. We find that theoretically single in situ (U–Th–Sm) He measurements from different grains from the same sample or multiple measurements within a single grain can be successfully inverted to retrieve consistently complex cooling histories similar to whole-grain analyses.
2.1 Modelling approach for He production, ejection, and diffusion
The in situ (U–Th–Sm) He method is based on the extraction of He, U, Th, and Sm from a small fraction of the grain using a laser ablation system (e.g. Boyce et al., 2006; Tripathy-Lang et al., 2013; Evans et al., 2015; Anderson et al., 2017; Pickering et al., 2020). Ablation pits can have a radius of a few tens of micrometres and depths of a few micrometres (e.g. from an excimer laser). Importantly, the ratio of He to U, Th, and Sm (and therefore the date) varies with the size and position of the laser ablation measurements and likely differs from corresponding whole-grain (U–Th–Sm) He dates. This, however, does not mean that dates are wrong or not interpretable; instead, they require a refinement of the interpretation steps commonly applied to (U–Th–Sm) He data.
Whole-grain (U–Th–Sm) He analyses often use a sphere-equivalent radius and assume spherical isotropic diffusion to estimate whole-grain He production, ejection, and diffusion in apatite and zircon crystals (e.g. Farley et al., 1996; Meesters and Dunai, 2002). More effort is required to match grain geometry for the in situ (U–Th–Sm) He method since long alpha-stopping distances (up to several tens of micrometres) result in a complex geometric relation between the location of radionuclides (U, Th, and Sm) and the resulting position of produced He. Most apatite grains have a prismatic geometry, with typical length-to-radius ratios of 4–8 (Farley, 2000). Loss of He by ejection and diffusion mostly occurs perpendicular to the crystallographic c axis in prismatic grains such as apatite and zircon, and thus the He profile should be approximated for most grains with a finite-cylinder model (Meesters and Dunai, 2002). Farley et al. (2011) provide a method to transform measured element concentrations from cylindrical grains into an equivalent spherical geometry, thereby providing input in the commonly used modelling software HeFTy (e.g. Danišík et al., 2017). Complementary to this approach, here we used the available spherical model implemented in HeFTy (Ketcham, 2005) and modified it to handle an infinite-cylinder geometry. The latter should be a good approximation for in situ measurements outside the tips or caps of the analysed grains where alpha-ejection effects become more significant. The advantage of an infinite-cylinder model (compared to a finite-cylinder model) is that it can be solved in 1D and thus runs as fast as the spherical model, a prerequisite for applying efficient inverse thermal history modelling. We adjusted the available He production, ejection, and diffusion models implemented in HeFTy (Ketcham, 2005; Flowers et al., 2009; Guenthner et al., 2013) to handle an infinite-cylinder geometry. More specifically, we implemented our changes to the existing C code (kindly provided by Richard Ketcham) that simulates He diffusion following the RDAAM (apatite, Flowers et al., 2009) and ZRDAAM (zircon, Guenthner et al., 2013) diffusion and annealing models. The modified version of RDAAM and ZRDAAM code is available from the associated Zenodo repository (https://doi.org/10.5281/zenodo.13898183, Glotzbach, 2024).
2.2 Geometric considerations for He production, ejection, and diffusion
The amount of He produced vs. ejected and diffused out of the grain depends on the concentration and distribution of parent isotopes and the grain morphology. These effects differ in spherical and cylindrical grains, especially if grains are zoned. Spherical zonation has been implemented in diffusion models for spheres (e.g. in HeFTy), which we also explore here for an infinite-cylinder geometry. For simplicity, we assume that radionuclide zoning is symmetric around the c axis for cylindrical grains (Fig. 2). Note that this might not always be applicable, especially for zircon grains, which apart from concentric parent nuclide distributions also reveal patchy or chaotic patterns (e.g. Chew et al., 2017; Danišík et al., 2017; Fox et al., 2017). It is therefore recommended that such a simplified approach is only applied to grains satisfying concentric parent nuclide distributions. Radionuclide zoning and grain size (especially the distance to the grain rim) control the amount of He along the radius (r axis) without diffusion. The He distribution along the r axis is derived by calculating the intersecting lines of all alpha-ejection spheres (ranging from ∼ 6 to ∼ 40 µm) and internal cylinders with a radius defined by the grain size and grid spacing. The intersection line can consist of two closed curves; a continuous line; or, if the cylinder and the sphere are tangential to each other at one point, the line forms an “eight” geometry, also known as Viviani's curve (Fig. 2a).
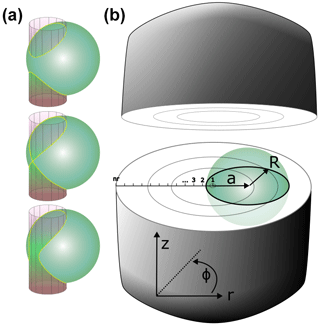
Figure 2Geometric relationship between alpha-ejection spheres (green) and intersecting inner-grain coaxial cylindrical surface representing variable radionuclide concentrations in a cylindrical grain (light grey lines). (a) The length of a line defining the intersection between the cylinder and a sphere depends on the size of each object and its position. (b) Assumed cylindrical grain with radionuclide zoning parallel to the z axis is intersected by an alpha-ejection sphere with radius R and distance from the centre of (a). The modelled He profile is discretized from the centre of the grain to the rim with nodes from i=1…nr.
The procedure for calculating the amount of He in an infinite cylinder without diffusion along the r axis is as follows.
-
The grain is discretized by a number of cylinders (, and the circular shape of the cylinders in r,Φ plane is transformed in x,y coordinates:
-
The z coordinates of the intersection line between the cylinder and the alpha-ejection sphere (the yellow line in Fig. 2a) are calculated with
where R is the radius of the alpha-ejection sphere, a is the distance between the centre of the cylinder and the alpha-ejection sphere, and Φ and r are the same as in Fig. 2b.
-
The length of the intersection line is calculated with the Pythagorean theorem:
where Φ has been discretized from 0 to 2π into i=1…nΦ.
-
Next, the length is normalized to unity:
where a has been discretized from r=0 to the rim into i=1…na.
-
Finally, we derived the radionuclide-specific concentration (CI,a) for isotopes (I) and points (a) along the r axis with
where FI,j is the fractional contribution of an isotope-specific stopping distance and C is the radionuclide concentration depending on r.
The resulting He distribution is very similar to a spherical grain but with an overall higher concentration (for similar radii) since we assume an infinite length of the cylinder (Fig. 3a, b). Consequently whole-grain and in situ (U–Th–Sm) He dates of a cylindrical grain are significantly older (in situ: 19 %–27 %; whole-grain: 11 %–12 %) compared to a spherical grain with similar radii (Fig. 3c, d). Incorporating He diffusion and alpha-stopping distances leads to smooth (uniform radionuclides) or complex (zoned grains) He profiles (Figs. 3, 6).
2.3 Calculation of He diffusion
Assuming a spherical grain geometry provides a good estimate of whole-grain He diffusion in apatite crystals (e.g. Farley et al., 1996; Meesters and Dunai, 2002). However, most apatite and zircon grains have a prismatic shape with hexagonal (apatite) and quadratic (zircon) cross sections. Efficient modelling of He profiles requires a 1D solution of the diffusion equation and therefore a round cross section, which can accurately predict He concentrations in apatite and zircon (cf. Eqs. 19 and 20 and Sect. 2.5). In the following, we solved the production and diffusion equation for an infinite cylinder (Farley, 2000). The 3D diffusion equation in a cylinder is
where v is the He quantity; K is the diffusivity; t is time; A0 is the volumetric He production; and r, z, and ϕ are the radial, vertical, and azimuth positions, respectively (e.g. Fig. 2b). Assuming an infinite length of the cylinder and that He does not vary with z and ϕ, the equation (Eq. 7) simplifies to
Using the product rule, we get
We solved Eq. (9) with an implicit Euler finite-difference method with the following assumptions: (i) grain symmetry (including geometry and radionuclide distribution) around the z axis, (ii) zero-flux Neumann boundary condition in the centre of the grain (Eq. 10), and (iii) zero He concentration at the grain boundary (Eq. 11):
Reformulating equation (Eqs. 9 and 10) with the implicit Euler method yields:
Since is not defined but is similar to , it is common to instead use the second derivative and Eq. (13) changes to
Solving Eq. (14) requires a tridiagonal matrix whereby all unknowns (t+1) are brought to the left-hand side:
where D is , and the corresponding tridiagonal matrix needed to solve for diffusion in an infinite cylinder is given by
The resulting He profiles for infinite cylinders have similar shapes to a sphere but higher He concentrations than a sphere with the same radius (Fig. 3a, b). The difference in concentration between the infinite-cylinder and sphere geometry (for constant cooling) is in the range of 15 %–20 % in the centre of the grain, comparable to previous observations (Meesters and Dunai, 2002). Corresponding in situ dates are 19 %–27 % older in an infinite cylinder compared to a sphere model with a similar grain radius, while whole-grain dates (not shown) differ by 11 %–12 %. The choice of geometry to model in situ (U–Th–Sm) He dates matters even more than for the whole-grain method.
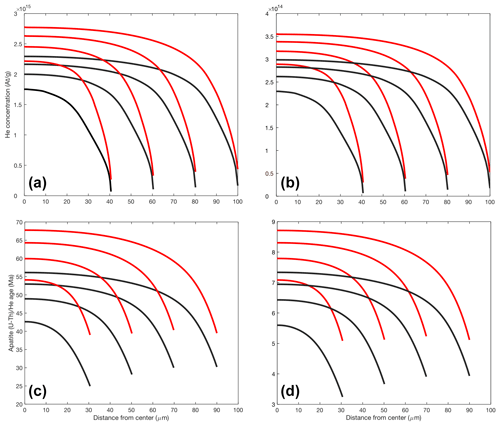
Figure 3Difference between He diffusion profiles and in situ (U–Th–Sm) He dates in a sphere (black) and infinite cylinder (red) perpendicular to the c axis with grain radii of 40, 60, 80, and 100 µm. All profiles are calculated for apatite grains applying the production, ejection, and diffusion with homogenous U, Th, and Sm distributions (10 ppm) and constant cooling rates of 1 °C Myr−1 (a, c) and 10 °C Myr−1 (b, d). In situ (U–Th–Sm) He dates of infinite-cylinder grains are 19 %–27 % older compared to spheres with similar radii, whereas corresponding whole-grain (U–Th–Sm) He dates differ by 11 %–12 %.
A cylindrical model is a good approximation for the He profile in hexagonal apatite grains (Meesters and Dunai, 2002), but it is unclear what radius should be used to estimate the He profile. To determine the appropriate cylinder radius to approximate diffusion in a hexagonal grain, we calculated the 2D (cross-sectional) He distribution of an infinitely long symmetrical hexagonal grain with a circumradius rc of between 30–50 µm and corresponding infinite cylinders with variable radii. We calculated the difference between the mean He profile of the hexagonal and cylindrical grains and found that the circle-equivalent radius (CER) of a symmetrical hexagonal grain is simply the radius of a circle with a similar area:
where r is the outer radius (touching all vertices) of a symmetrical hexagon. Equivalent to a zircon with a quadratic cross section, we derived the following:
where r is the outer radius of a quadrate.
2.4 Implementation of alpha-stopping distances
During alpha decay, energy is released that leads to long alpha-stopping distances (e.g. Bragg and Kleeman, 1905). The common radiogenic isotopes 238U, 235U, 232Th, and 147Sm release alpha decay energies between 2233 keV (147Sm to 143Nd) to 8784 keV (212Po to 208Pb as part of the decay chain of 232Th). In total, the alpha decay of these radionuclides produces 216 different energies, each occurring with a different probability (Fig. 4). The relation between energy and stopping distance has been measured and calculated and is easily accessible from the SRIM data collection (e.g. Farley et al., 1996; Ketcham et al., 2011). Alpha particles produced from 238U, 235U, and 232Th have stopping distances between ∼ 11 and ∼ 40 µm in apatite (Fig. 4a–c), and those derived from 147Sm have a single stopping distance of ∼ 6 µm. Integration of the stopping distance distribution yields the average stopping distances (Fig. 4a–c), commonly used to approximate He distribution profiles and FT correction factors for whole-grain analyses (e.g. Ketcham et al., 2011). Note that the reported values using the SRIM 2013 data show only very small differences from those of Ketcham et al. (2011), which is based on SRIM 2008.

Figure 4Alpha particle energy spectra of 238U (a), 235U (b), and 232Th (c) and the corresponding stopping distance spectra and mean stopping distances derived from SRIM2013 data assuming a fluorine apatite with a density of 3.2 g cm−3. The stopping distance distribution (SD dist.) of a typical apatite with 20 ppm U and Th and 100 ppm Sm is shown in (d).
Depending on the relative concentration of radionuclides, each mineral crystal will have a grain-specific alpha-stopping distance distribution (Fig. 4d). The majority of stopping distances in apatite are between 11 and 26 µm, with additional peaks at 6, 32, and 39 µm for a common apatite (Fig. 4d). Stopping distances in zircons are shorter and less variable, ranging from 9 to 32 µm, while the majority are between 10 and 26 µm long (Fig. S1 in the Supplement). Due to the long alpha-stopping distances, the He measured in situ in an infinitely small area within the grain is produced from the surrounding ∼ 6 to 39 and ∼ 9 to 32 µm in apatite and zircon, respectively. Importantly, He originates from the surface of spheres with a radius corresponding to the stopping distance distribution (Figs. 2, 5). This does not have large consequences for grains with a homogenous radionuclide distribution, but He and radionuclide distributions do not follow a 1:1 relation in the case of radionuclide heterogeneity in grains (Fig. 5).
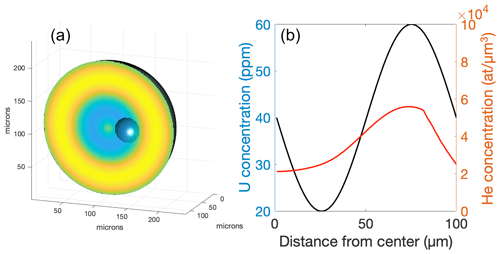
Figure 5Relationship between radionuclide zonation and resulting He profiles in a spherical apatite grain. (a) Spherical grain with radial U, Th, and Sm concentrations between 20 to 60 ppm, respectively. The small half-sphere corresponds to a stopping distance of 20 µm. (b) U, Th, Sm, and resulting He concentrations from the core to the rim of the grain shown in (a).
As a consequence, we adjusted the original RDAAM and ZRDAAM c implementation of HeFTy to (i) handle the full spectrum of stopping distances (instead of using an averaged value) of respective radionuclides and (ii) incorporate inner-grain radionuclide variations.
We tested our extended implementation against the original implementation for a theoretical spherical apatite grain (Fig. 6). The resulting whole-grain dates are indistinguishable from each other, but the He profiles produced are smoother and in some cases show distinct differences (Fig. 6). Considering the full spectrum of stopping distances results in an overall lowering of the He concentration when approaching the grain rim for uniform radionuclide distributions (Fig. 6a). The incorporation of longer stopping distances (up to 39 µm) results in reduced He production at a distance between the longest stopping distance and the mean stopping distance from the grain rim. The opposite effect (higher He concentrations nearer to the grain rim) originates from stopping distances shorter than the mean stopping distance (Fig. 6a). Spherical grains with a grain radius smaller than the longest stopping distance (39 µm) but larger than the mean stopping distance (∼ 20 µm) show lower He concentrations since the production in the grain core is zero when the grain radius is smaller than the stopping distance (Fig. 6a). Variations in radionuclides, such as at the boundary between the grain and exterior, require consideration of the full spectrum of stopping distances for the case of in situ (U–Th–Sm) He analyses close to the grain rim (within 39 µm from the grain rim). Similarly, a mean stopping distance approach results in dissimilar He profiles in zoned grains with radionuclide variations compared to considering the full spectrum (Fig. 6b). To give an example, a 2 times higher radionuclide concentration between half and three-quarters of the radius (measured from the centre) results in the largest differences in the He concentration in the centre of the grain. The latter is usually the target of in situ (U–Th–Sm) He analyses. We suggest that any in situ (U–Th–Sm) He analyses require considering the full spectrum of significantly contributing alpha-stopping distances. Although not investigated here, the method might also benefit from considering this to predict more accurate He profiles (e.g. Shuster and Farley, 2004).

Figure 6Apatite He profiles and (U–Th–Sm) He dates for a cooling rate of 1 °C Myr−1, variable grain sizes, and mean (red, original implementation) or complete stopping distances (blue, our implementation). (a) Uniform U, Th, and Sm concentration of 10 ppm. (b) The same as in (a) but with 2 times higher radionuclides between the half radius and one-third radius.
2.5 Circle equivalent radius (CER)
Modelling of (U–Th–Sm) He data is usually accomplished using a transient 1D axial-symmetric parameterization, where different grain morphologies are approximated with a spherical geometry with similar volume-to-surface area ratios. With this approach, a solution is calculated in 1D (as a function of radius) and then integrated over the volume of the equivalent sphere. It has been shown that this approach is accurate for common grain morphologies within a few percent, whereas an infinite cylinder can have a deviation of up to 7 % (e.g. Meesters and Dunai, 2002). Here we explore if such an approach also applies to accurately estimating He profiles within grains. We modelled the He distribution of an infinite symmetrical hexagonal prism with an outer radius of 50 µm (inner radius of 43.3 µm). We compared these results to those calculated with an infinite cylinder (Fig. 7). The CER for such a grain is ∼ 45.5 µm. The mean He profile of the hexagonal prism after averaging all possible profiles from the centre of the grain to the edge are nearly identical to a cylinder with a radius of 45.5 µm. This result is irrespective of the cooling history (Fig. 7). The He profile deviates substantially at the outermost 5–10 µm between the long and short axis of a hexagon, which should be discarded if it is not known exactly where the short and long axes are relative to the location of measurement.
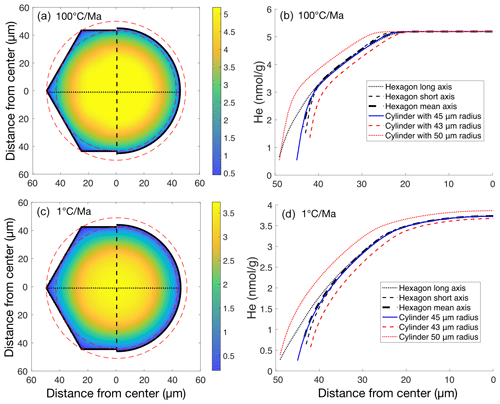
Figure 7He concentration in infinite hexagonal prism and cylinder. (a) He concentration map modelled with RDAAM for a symmetrical hexagonal prism with an outer radius of 50 µm and a cylinder with a radius of 45.5 µm; 10 ppm U, Th, and Sm concentrations; and rapid cooling (100 °C Myr−1) to surface temperature (10 °C) at 60 Ma. (b) Corresponding He profiles for a hexagonal prism and infinite cylinder with different radii. Panels (c) and (d) are similar to panels (a) and (b), respectively, but for a constant cooling rate of 1 °C Myr−1.
2.6 Analytical uncertainty
In situ (U–Th–Sm) He dating relies on measuring pits that are only a few tens of micrometres in size, leading to increased analytical uncertainty, particularly in He measurements, compared to conventional whole-grain analyses. A typical cylindrical grain used in whole-grain measurements, with a diameter of 100 µm and a length of 200 µm, has a volume approximately 1000 times greater than a standard in situ pit with a diameter of 30 and 5 µm depth. Consequently, in situ analyses face significant analytical uncertainties, especially when applied to young samples or grains with low radionuclide concentrations. To report these limitations, we used the detection limit determined in our laboratory at the University of Tübingen to model analytical uncertainties. The standard deviation of repeated line blanks (SDlb) gives a 4He of 0.000079 ncc or 2.11 × 106 atoms. This allows for estimating the analytical uncertainty for modelled in situ He content (4Hem) using the following equation:
This equation does not account for uncertainties related to the required measurement of radionuclides, which are generally small and around 2 %.
3.1 Whole-grain vs. in situ (U–Th–Sm) He dates
Whole-grain (U–Th–Sm) He dates reflect the production, ejection, diffusion, and alpha-ejection correction for the complete grain. In contrast, in situ (U–Th–Sm) He dates, if measured in the centre of grains, are not affected by alpha ejection, are less affected by diffusion, and do not require an alpha-ejection correction (e.g. Tripathy-Lang et al., 2013). Theoretically, in situ dates will, in most cases, differ from whole-grain dates from similar grains. The majority of in situ (U–Th–Sm) He studies applied so far used large crystals with homogenous radionuclide distributions and/or rapidly cooled samples to enable comparison of the results to whole-grain measurements (e.g. Boyce et al., 2006; Horne et al., 2016). Making this method applicable to small and/or slowly cooled grains requires understanding the relationship between the grain size, position and size of the ablation spots, radionuclide distribution, and resulting (U–Th–Sm) He dates. To investigate these effects we considered several scenarios.
First, we modelled whole-grain and in situ (U–Th–Sm) He dates as a function of cooling rate (1, 10, and 40 °C Myr−1) for radionuclide concentrations of 10 ppm and a grain radius of 100 µm (Fig. 8a–c). Modelled whole-grain dates are 49, 6.5, and 1.9 Ma for cooling rates of 1, 10, and 40 °C Myr−1, respectively. In situ (U–Th–Sm) He dates vary as a function of their measurement position in the grain. Assuming similar grain parameters and cooling rates, in situ dates range between 48–65 Ma (1 °C Myr−1), 6.3–8.3 Ma (10 °C Myr−1), and 1.8–2.4 Ma (40 °C Myr−1) for a spot diameter of 20 µm and grain radius of 100 µm (Fig. 8a–c). Modelled in situ dates measured in the centre of grains are older than the whole-grain dates because the fraction of He lost by diffusion is smallest in the centre of grains and increases towards the grain boundary, as does He loss by alpha ejection. Accordingly, in situ dates become progressively younger towards the grain rim. A larger laser spot size averages over a larger area and may incorporate areas affected by He loss. A larger spot size therefore leads to younger dates, and a smaller spot size can be expected to produce less variation in dates, especially when analysing smaller grains. Modelled analytical uncertainties limit the applicability of the in situ (U–Th–Sm) He method for young grains (Fig. 8a, b). A spot diameter > 50 µm and therefore a grain with a diameter of ∼ 100 µm is required to reach uncertainties < 100 % for dates < 10 Ma (Fig. 8a, b).
Second, we simulated the effect of grain size on whole-grain and in situ (U–Th–Sm) He dates for a cooling rate of 1 °C Myr−1; radionuclide concentrations of 10 ppm; and grain radii of 100, 80, 50, and 40 µm (Fig. 8c–f). Whole-grain dates decrease as a function of grain size from 49 to 39 Ma, while in situ dates consistently result in older dates. In situ measurements with similar spot diameter (e.g. 20 µm) sample larger fractions of areas affected by He loss and therefore in situ dates become less sensitive to the measurement position in the grain for smaller grains. In the most extreme case where the spot diameter corresponds to the grain radius the alpha-ejection-corrected in situ date would match the whole-grain date. In practice, the spot size also depends on the expected He concentration and must be determined based on the detection limit of He measurable with the instrumental setup and the maximum depth of laser pits that can be measured accurately.
Third, we studied the in situ date dependency for cases in which grains have not been ground and polished to the exact centre of the grain (Fig. 8g, h). In situ dates become progressively younger towards the grain rim compared to a measurement in the centre of the grain (Fig. 8g, h). In a large grain (100 µm radius, Fig. 8g), dates are similar within < 40 µm from the central plane of the grain. In situ dates in smaller grains are more sensitive to the position of the measurement relative to the grain rim (Fig. 8h).
In summary, uniform cooling yields in situ (U–Th–Sm) He dates that are older than whole-grain dates, and dates strongly vary as a function of the measurement position relative to the grain rim. The results obtained here for apatite also apply to zircons, as has been revealed by modelling in situ dates as a function of grain size and the position and size of the ablation spots with the ZRDAAM approach (Fig. S2). Measuring grain size and geometry and the laser spot position relative to the grain rim is essential for correctly interpreting in situ (U–Th–Sm) He dates. The grain size and geometry and location of laser pits on the grain surface can be easily determined with an optical microscope, whereas estimating the pit location in the vertical direction is difficult. A rough estimate (±5 µm) can be gained by focusing on the contact between grain and embedding media and measuring the distance to the exposed grain surface.
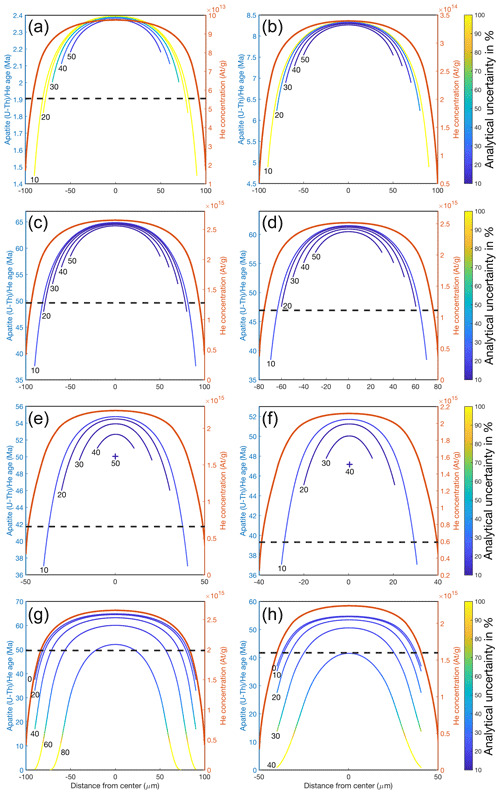
Figure 8Predicted in situ apatite (U–Th–Sm) He dates (blue to yellow lines) and He concentration profile (orange line) for an infinitely long, cylindrical-shaped apatite with homogenous radiogenic nuclide distribution (U, Th, and Sm concentration of 10 ppm). Predicted dates are calculated by integrating the modelled He distribution over an entire ablation pit volume of variable diameters (black numbers on curves in (a)–(h)), which is continuously measured across the grain. In reality, discrete (rather than continuous) pits would be measured, and smooth curves such as those shown here would not be possible. In situ date profiles are colour coded according to expected analytical uncertainties calculated with an observed standard deviation of the 4He blank of 0.000079 ncc. (a) Model results assuming a constant cooling rate of 40 °C Myr−1 to a final temperature of 10 °C and a grain radius of 100 µm. The corresponding whole-grain date for a sphere with a similar sphere-equivalent radius (radius × 1.5) corrected for alpha ejection is 1.9 Ma. Modelled in situ dates with variable spot diameters (10, 20, 30, 40, and 50 µm) range from 2.4 Ma in the centre of the grain to 1.45 Ma half the spot diameter away from the grain rim. (b) Model results assuming constant cooling at 10 °C Myr−1 to 10 °C and a grain radius of 100 µm. The corresponding whole-grain date corrected for alpha ejection is 6.5 Ma. Modelled in situ dates with variable spot diameters (10–50 µm) range from 8.3 Ma in the centre of the grain to 4.8 Ma at half the spot diameter away from the grain rim. (c) Model results assuming constant cooling at 1 °C Myr−1 to 10 °C and a grain radius of 100 µm. The corresponding whole-grain date corrected for alpha ejection is 64.9 Ma in the centre of the grain to 37.7 Ma at half the spot diameter away from the grain rim. (d, e, f) The same as (c) but with a grain radius of 80, 50, and 40 µm, respectively. The smaller grain radius results in younger whole-grain dates (47, 42, and 39 Ma, respectively) and a stronger relationship between in situ dates and distance of measurement towards the grain rim. (g) In situ dates for a grain radius of 100 µm and spot diameter of 10 µm. Dates have been calculated for the central plane, dividing the cylinder into two symmetrical sides along the crystallographic c axis (black number 0–0 µm in the r direction of Fig. 2) and planes cutting the grain at 20, 40, 60, and 80 µm above or below the central plane. (h) In situ dates for a grain radius of 50 µm and spot diameter of 10 µm. Dates have been calculated for the central plane and at other r planes at 10, 20, 30, 40 µm.
3.2 Effects of radionuclide zoning
Without practical analytical measurement methods to quantify inner-grain variations in radionuclides, whole-grain analyses commonly use an a priori assumption of a uniform radionuclide distribution. The in situ (U–Th–Sm) He dating technique produces spatially resolved (albeit averaged over the ablation pit) measurements of U, Th, and Sm (e.g. Horne et al., 2016; Danišík et al., 2017). In situ measurements can provide information about inner-grain radionuclide variations and potentially lead to a reduction in date variability when excluding grains with radionuclide variations or by taking into account heterogeneities in the radionuclides.
Ideally, however, the 2D–3D distribution of parent nuclide concentrations is mapped in grains, which is possible with a new generation of instruments, such as by mapping parent nuclide concentrations with laser ablation inductively coupled plasma mass spectrometry (Chew et al., 2017), time-of-flight secondary ion mass spectrometry (North et al., 2023), or synchrotron X-ray fluorescence tomography (Sousa et al., 2024). Measured 3D radionuclide patterns can be incorporated in available implementations of 3D modelling of He production, ejection, and diffusion (e.g. Gautheron et al., 2012). Although this procedure would be ideal, it is computationally and analytically expensive and therefore not routinely applied. Efficient thermal history modelling of (U–Th–Sm) He data requires 1D modelling of He production, ejection, and diffusion, which can be combined with time-efficient single-spot LA-ICP-MS measurements. This approach should be used to identify and exclude grains with complex radionuclide variations.
Here, we have analysed several hundred LA-ICP-MS measurements done in our lab at the University of Tübingen, Germany. The depth-resolved radionuclide measurements in apatite and zircon demonstrate that radionuclide zoning is common (Sect. S1 in the Supplement). Zoning is more common and pronounced in zircons: ∼ 30 % of all analysed zircons have a core-to-rim ratio of < 0.5 or > 2, whereas this fraction is at ∼ 10 % for apatites (Fig. S4). Not accounting for radionuclide zoning results in erroneous Ft correction factors and resulting whole-grain dates (e.g. Hourigan et al., 2005). Here, we use our updated production-ejection-diffusion model to calculate the relationship between whole-grain (U–Th–Sm) He dates and radionuclide variations (Fig. 9).
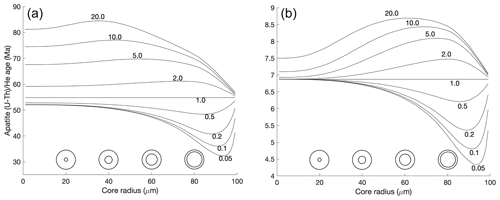
Figure 9Whole-grain apatite (U–Th–Sm) He dates as a function of radionuclide variations (zoning). Isoline labels correspond to the core-to-rim ratio of radionuclides, assuming a single-step function in the concentration of U, Th, and Sm across the grain, where the x axis specifies the location of the step in concentration. (a) Dates for a cooling rate of 1 °C Myr−1 and volume-averaged U, Th, and Sm concentration of 10 ppm. (b) Dates for a cooling rate of 10 °C Myr−1 and volume-averaged U, Th, and Sm concentration of 10 ppm.
Commonly observed core-to-rim ratios between 0.5 and 2 lead to ±10 % date deviations (Fig. 9). Since observed radionuclide variations cannot be simplified with a single-step function (Fig. S3), we have scaled measured LA-ICP-MS-derived depth variations to a grain radius of 100 µm and calculated whole-grain apatite and zircon (U–Th–Sm) He dates for a cooling rate of 1 °C Myr−1 (Fig. 10; for details, see Sect. S2 in the Supplement). Single-grain dates are mainly a function of the mean eU of individual grains, but depending on the amount of radionuclide zoning, dates deviate from the corresponding date assuming homogenous radionuclide distribution (red line in Fig. 10). The correlation coefficient is 0.95 and 0.77 for all apatites and zircons, respectively, or in other words 5 % and 23 % of the variability in dates, respectively, is the result of radionuclide zoning. Individual samples usually involve fewer grains with variations in dates caused by radionuclide zoning ranging from 1 % to 40 % and 19 % to 84 % for analysed apatites and zircons (Fig. 10), respectively. In samples with a low variation in eU and strong radionuclide zoning, the majority of variability is caused by zoning, and there is no significant relation with eU. For example, in the analysed Fish Canyon tuff zircons, 84 % of the variations in dates is due to zoning (Fig. 10b). As mentioned earlier, additional age dispersion can come from crystal fragmentation, radionuclide-rich inclusions, fluid inclusions, and implantation of He from the exterior (e.g. Brown et al., 2013; Vermeesch et al., 2007; Spiegel et al., 2009; Danišík et al., 2017). It is, therefore, more likely to have over-dispersed whole-grain (U–Th–Sm) He dates, and perfect relations between dates and eU will be the exception rather than the rule (Flowers et al., 2023).
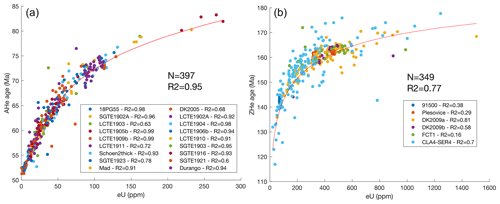
Figure 10Simulated apatite (a) and zircon (b) (U–Th–Sm) He dates for a constant cooling rate of 1 °C Myr−1 and measured grain-specific U, Th, and Sm variations (coloured dots). Radionuclide variations were measured in age standards and random samples with a LA-ICP-MS system and scaled to a common grain size of 100 µm, assuming symmetric zoning around the c axis. This was used to model grain-specific whole-grain (U–Th–Sm) He dates. The red line represents the relation between dates and homogenous radionuclide distribution. The correlation coefficient for the whole dataset and individual samples are shown. Note that the 1−R2 is the fraction of spread caused by radionuclide zoning.
The observed radionuclide variations and resulting date dispersion in Fig. 10 allow for estimating the minimum sample size required to reach a defined correlation coefficient between the date and eU. We did this by randomly sampling grains from our database 20 000 times and determined the relationship between the correlation coefficient and sample size. We found that a minimum of 10 apatite grains is needed to reach an R2 of 0.8 and that an impractical amount of whole-grain ZHe dates (23) are theoretically needed to reach a minimum R2 of 0.5 (see Sect. S3 in the Supplement for details).
In summary, whole-grain (U–Th–Sm) He age variations with eU are often biased by radionuclide zonation. In in situ (U–Th–Sm) He studies, radionuclides are typically determined from a single pit, several tens of micrometres deep, drilled and analysed using LA-ICP-MS (e.g. Pickering et al., 2020). After applying a downhole fractionation correction to those data (Paton et al., 2010), depth-resolved radionuclide profiles in apatite and zircon grains enable the identification of zoned grains, which should be excluded from further analyses. Since this analytical step is mandatory for the in situ (U–Th–Sm) He method, single-grain data should, in theory, lead to less dispersion in date vs. eU plots and likely also produce more reliable thermal history reconstructions. In contrast, including grains with identified radionuclide zoning is likely to produce inaccurate results, as helium is generated and measured from different volumes within the grain (e.g. Vermeesch et al., 2023).
3.3 Thermal history modelling of in situ (U–Th–Sm) He data
The relative distribution of He within an apatite or zircon grain is a function of the distribution of radionuclides, grain morphology, and the cooling history. A suite of whole-grain analyses can be used to reconstruct potential cooling histories under the precondition that analysed grains have different grain sizes and/or eU (e.g. Ketcham, 2005; Flowers et al., 2009; Gautheron et al., 2009; Guenthner et al., 2013). This approach, however, has the risk of including grains with internal variations in radionuclides and is therefore often applied in combination with other thermochronometric systems (e.g. apatite fission track data). Similar to whole-grain analyses, radionuclide zonation can bias the interpretation of cooling histories derived from the apatite method (Farley et al., 2010), which indirectly measures the He profile by a stepwise degassing of He from proton-irradiated apatite grains.
Thermal history modelling with in situ (U–Th–Sm) He data could be done by (i) measuring multiple grains that vary in size and/or eU similar to the whole-grain approach or (ii) reconstructing the He profile with multiple measurements in a single grain comparable to the method (e.g. Danišík et al., 2017). Both approaches are applied in the following to reconstruct common cooling paths from synthetic datasets. A robust methodology requires knowing or estimating (i) the grain geometry, (ii) the position of the in situ measurements within the grain, and (iii) the radionuclide distribution within the grain and (iv) building an appropriate model to account for the previous factors.
In theory, complex grain morphologies could be used for such an approach, but this would require implementing grain-specific 3D models. Thermal history modelling with 3D models is a time-consuming process and is therefore not practical for routine analysis. Similar to whole-grain analyses, it is therefore recommended to make in situ measurements of grains with simple geometries characterized by straight and/or 2D–3D constant curvatures such as spherical, elliptical, and cylindrical shapes. Preferably, the in situ measurement can be approximated with a 1D modelling approach similar to whole-grain and analyses, where the sphere-equivalent radius has been shown to be a good approximation (e.g. Meesters and Dunai, 2002; Farley et al., 2010). Unlike whole-grain and analyses, the in situ method requires modelling the He concentration within the ablated pit volume.
We conducted three different measurement approaches to evaluate the utility of in situ dating techniques for thermal history reconstruction. First, a set of two cylindrical spots with 30 µm diameter and 5 µm depth in the centre of cylindrical-shaped grains with radii of 80 and 40 µm and similar eU were forward-modelled with three different cooling histories: (1) a constant cooling rate of 1 °C Myr−1; (2) rapid cooling of 100 °C Myr−1 at 60 Ma to surface temperature followed by no cooling; and (3) a step increase in cooling rate from an initial 1 °C Myr−1 until 10 Ma to 50 °C, followed by 4 °C Myr−1 cooling to surface temperature. Analytical uncertainties in theoretical He measurements were calculated with Eq. (21) and lab-specific blank levels (2.11 × 106 atoms), resulting in uncertainties of ∼ 8 % for cooling histories (1) and (2) and ∼ 15 % for cooling history (3). Several thousand forward models were conducted, and the goodness-of-fit (GOF) parameter of predicted cooling paths was determined. We used the same definition of the GOF and colour scheme as used in HeFTy (Ketcham, 2005). Good and acceptable model paths retrieve the input He profile and cooling paths, especially in the centre of grains, while modelled He concentrations deviate in the outer 20 µm for some or most cooling paths (Fig. 11).
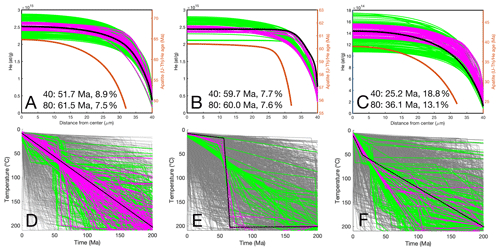
Figure 11Modelling of cooling histories for three synthetic datasets with two laser ablation spot measurements in apatite grains with a pit diameter of 30 µm (5 µm depth); a grain radius of 80 and 40 µm; and U, Th, and Sm concentrations of 10 ppm. The upper panels (a, b, c) show the synthetic (black line) and modelled (green, magenta) He profiles, while the brown line represents the in situ (U–Th–Sm) He dates for the 40 µm grain (see Sect. S4 in the Supplement for corresponding whole-grain dates and He profiles of the 80 µm grain). The lower panels (d, e, f) show the input (black) and modelled (grey, green, magenta) cooling paths. Predicted cooling histories with acceptable paths are green (GOF > 0.05), good paths are magenta (GOF > 0.5), and paths with a GOF < 0.05 are grey. (a, d) Data were calculated with a constant cooling rate of 1 °C Myr−1. (b) Input data were modelled with rapid cooling at 60 Ma to surface temperature. (c) Initial slow cooling with 1 °C Myr−1 to 50 °C at 10 Ma is followed by faster cooling to the surface with 4 °C Myr−1.
Second, a set of synthetically generated He measurements were taken along a profile in a single grain. We use a cylindrical grain with a radius of 100 µm and the same thermal histories as in the previous experiment. We sampled the He profile with an assumed cylindrical spot with a diameter of 20 µm and depth of 5 µm at five locations from the centre of the grain to the rim. The resulting He profiles and synthetic He measurements with uncertainties are shown in Fig. 12a–c. Analytical uncertainties in theoretical He measurements were calculated with Eq. (21) and lab-specific blank level (2.11 × 106 atoms), resulting in uncertainties of 16 %–20 % for cooling history (1) and (2) and ∼ 26 %–40 % for cooling history (3). Most acceptable cooling histories overlap or are close to the input parameters, suggesting that in situ (U–Th–Sm) He measurements within a single grain can be used to get information on its cooling history (Fig. 12d–f).

Figure 12Cooling histories predicted from in situ (U–Th–Sm) He measurements sampled along the He profile of a synthetic cylindrical apatite grain with a radius of 100 µm and U, Th, and Sm concentrations of 10 ppm. Five 20 µm diameter (5 µm depth) ablation pits across the grain (horizontal black lines) are used as synthetic input data. The upper panels (a, b, c) show synthetic (black line) and modelled (green, magenta) He profiles, while the brown line represents the in situ (U–Th–Sm) He dates. Resulting in situ (U–Th–Sm) He dates and He uncertainties are also given from the centre (left) to the rim (right). The lower panels (d, e, f) show the input (black) and modelled (grey, green, magenta) cooling paths. Predicted cooling histories with acceptable paths are green (GOF > 0.05), good paths are magenta (GOF> 0.5), and paths with a GOF < 0.05 are grey. Data are modelled with a constant 1 °C Myr−1 cooling rate (a, d), a rapid cooling event at 60 Ma to surface temperature (b, e), and slow cooling with 1 °C Myr−1 to 50 °C followed by faster cooling to the surface with 4 °C Myr−1 from 10 Ma (c, f).
Although we would not recommend interpreting grains with internal radionuclide variations, here we investigate the consequences for in situ and whole-grain thermal history modelling. We assume a scenario in which the outer 10 µm of grains is enriched in radionuclides (U, Th, Sm: 50 ppm) compared to the grain interior (U, Th, Sm: 10 ppm). This is a nasty scenario, resulting in largely underestimated whole-grain (U–Th–Sm) He dates if not corrected for (Fig. 9). Analogous to the previous thermal history modelling, a fast cooling from high temperature to surface temperature at 60 Ma was used to produce theoretical (U–Th–Sm) He data for cylindrical grains with 100, 80, and 40 µm radii.
The general cooling trend can be retrieved in cases where the radionuclide distribution is precisely known and the He profile is sampled with several measurements in a single grain (Fig. 13a, b) or multiple grains with variable sizes are analysed (Fig. 13g–j). We also tested the inversion performance assuming a homogenous radionuclide concentration of 10 ppm, measured for instance with a LA-ICP-MS pit in the centre of the grain (not reaching the grain rim). In addition, a homogenous radionuclide concentration of 17.6, 19.4, and 27.5 ppm for grains with 40, 80, and 100 µm radii, respectively, was used as input, representing the grain-averaged concentration, as measured through whole-grain analyses. As expected, observed inner-grain He variations, with increased concentrations toward the grain rim, are impossible to model with a constant radionuclide concentration (Fig. 13c–k). The He concentrations in the centre of the modelled grains with radii > 40 µm are nearly unaffected by the high radionuclide concentration in the rim of the grain (e.g. Fig. 13a, g). In this specific scenario, modelling in situ (U–Th–Sm) He data from the centre of grains correctly retrieves the cooling when assuming a constant radionuclide concentration of 10 ppm (Fig. 13i, j). Instead, using the mean whole-grain radionuclide concentration as input results in incorrect cooling histories (Fig. 13k, l).
We modelled whole-grain (U–Th–Sm) He data to investigate the ability to reconstruct the input thermal history of zoned grains. Modelled whole-grain (U–Th–Sm) He values are between 57.3, 58.7, and 59.0 Ma for grains with 40, 80, and 100 µm grain radius, respectively, and rapid cooling to the surface temperature at 60 Ma. The whole-grain data can retrieve the general cooling trend in case the radionuclide distribution is precisely known (Fig. 13m). The latter, however, is commonly not measured, and instead the whole-grain average radionuclide concentration is measured and used for thermal history modelling. Interestingly, the modelling does not retrieve the correct or indeed any acceptable cooling history (Fig. 13o), which we interpret as a result of incorrect He diffusivities associated with the assumption of homogenous inter-grain-variable radionuclide concentrations (19.4 vs. 27.5 ppm). For comparison, we also modelled the thermal history using a radionuclide concentration of 10 ppm for both grains (Fig. 13n). Although acceptable and good thermal paths are predicted by inverse modelling, the correct input thermal history could not be retrieved.
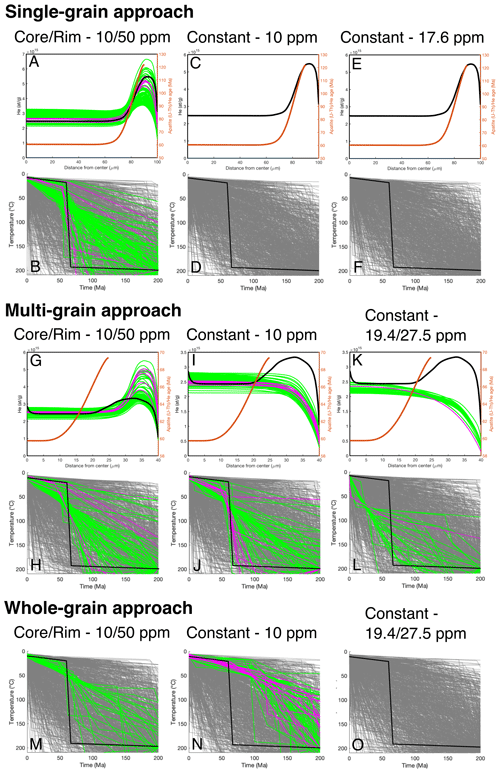
Figure 13Cooling histories predicted from in situ and whole-grain (U–Th–Sm) He measurements of a synthetic cylindrical apatite grain with a radius of 40, 80, and 100 µm and U, Th, and Sm concentrations of 10 ppm in the core and 50 ppm in the 10 µm wide rim. All input data are modelled with fast cooling to surface temperature at 60 Ma. Retrieving the thermal history assumes either (i) precise knowledge of the radionuclide variation and distribution (left column), (ii) a homogenous radionuclide concentration of 10 ppm (middle column), or (iii) whole-grain average homogenous radionuclide concentration (right column). (a–f) Single-grain approach with five 20 µm diameter (5 µm depth) ablation pits across a grain with 100 µm radius used as synthetic input data. The upper panels (a, c, e) show synthetic (black line) and modelled (green, magenta) He profiles, while the brown line represents the in situ (U–Th–Sm) He dates. The lower panels (b, d, f) show the input (black) and modelled (grey, green, magenta) cooling paths. Predicted cooling histories with acceptable paths are green (GOF > 0.05), good paths are magenta (GOF > 0.5), and paths with a GOF < 0.05 are grey. (g–l) Multi-grain approach using a central 30 µm diameter (5 µm depth) ablation pit in two grains (40 and 80 µm radii) as synthetic input data. (g–l) Similar to (a)–(f) but for a multi-grain approach. (m–o) Thermal inversion results for two grains with 40 and 80 µm radii using the whole-grain approach.
4.1 Synthesis of results
The previous results suggest that in situ (U–Th–Sm) He dating can provide an improvement in date and thermal history calculation compared to the conventional whole-grain analyses. This is due to the technique's capability to detect for radionuclide zoning, thereby resulting in reliable date predictions and thermal history reconstructions. The latter, however, can only be achieved when grains with radionuclide zoning are excluded because accounting for zoning would ideally require a 3D mapping and modelling approach that is not routinely feasible. However, a caveat of the in situ approach is that individual spot dates will be variable across the grain even without radionuclide zoning, and a framework is required for interpreting them.
Based on the previous analysis, we suggest two different measurement approaches for in situ (U–Th–Sm) He dates to yield geologically relevant data. These approaches include single-spot measurements from multiple grains from a single sample and multiple spot locations across a single grain. In both cases, potential inner-grain radionuclide variations need to be studied, for instance, making maps, creating line scans, or drilling through the whole grain with a LA-ICP-MS system. In addition, a combination of both single- and multiple-spot approaches might be practical, with single-spot measurements in small grains and multiple-spot measurements in larger grains. Regardless, the resulting dates can be used to reconstruct the sample's cooling history for cooling rates between 1–40 °C Myr−1. Faster cooling rates (e.g. 100 °C Myr−1) characteristic of rapidly exhuming orogens (e.g. Himalaya, Taiwan, New Zealand) were not explored in this study and may present additional challenges if parent radionuclide concentrations are low (e.g. 1–10 ppm), leading to low He concentrations that are below the detection limit using reasonable pit diameters (< < 100 µm).
Results presented here were based on simulated ablation pit diameters of 20 and 30 µm (5 µm deep) and U, Th, and Sm concentrations of 10 ppm. With these values, in situ dating of apatite grains as young as ∼ 60 Ma and analytical uncertainty of ∼ 10 % is possible (with our measurement limit of detection being 0.000079 ncc He). Accordingly, ages as young as 10 Ma can be measured with a pit diameter of 30 µm (10 µm deep). Increasing the pit volume further would be problematic for deriving the cooling history from in situ (U–Th–Sm) He data, especially if grains are small. Larger pit volumes more likely integrate areas of the grain affected by He ejection and limit the number of pits placed in a single grain. Given these factors, we recommend that future investigations of in situ analytical procedures analyse large grains and measure He in pit volumes that are as small as possible while remaining detectable for reconstructing thermal histories.
4.2 Meaning of in situ dates
Whole-grain (U–Th–Sm) He dates primarily depend on the sample cooling history and to a lesser degree vary with grain size, radionuclide concentration, and the alpha-damage density. In addition, they can occasionally be biased by radionuclide zoning or inclusions (e.g. Farley, 2002). In the rare case of rapid cooling to surface temperatures, the whole-grain date (irrespective of grain size and radionuclide concentration) reflects the time of that cooling event (e.g. Wolf et al., 1998). Importantly, the same date can be reproduced by slow monotonic cooling and even cooling followed by reheating (e.g. Wolf et al., 1998). In the latter case, the (U–Th–Sm) He date might even correspond to the time when the sample was at the surface temperature. A single whole-grain (U–Th–Sm) He date does not hold much information about its thermal history, which requires analysis of more grains or a joint interpretation with other thermochronology methods and geological constraints.
Our modelling of in situ and whole-grain (U–Th–Sm) He dates for slow to fast cooling rates (1–40 °C Myr−1) indicates that dates are commonly older than the corresponding whole-grain date for monotonic cooling (Fig. 8). In a study with a larger variation in parameters, we explored the relationship between whole-grain and in situ dates for very slow to fast cooling rates (0.5–40 °C Myr−1) in more detail (Fig. 14). Monotonic cooling, irrespective of the cooling rate, results in roughly 30 % older in situ dates compared to whole-grain dates (Fig. 14a, b). Cooling with a rate of 10 °C Myr−1 to a surface temperature of 10 °C at different times results in variable differences in whole-grain vs. in situ dates (Fig. 14c–d). Dates are nearly identical for cooling to surface temperature at 50 Ma, and dates diverge for cooling histories to surface temperatures at younger times.
The fundamental difference between whole-grain and in situ (U–Th–Sm) He dating is the location and volume where He is measured in a grain, whereas the differences in dates between the methods strongly depend on the cooling history and associated diffusion history. He production and ejection result in strong concentration differences in grains, which set the pace for diffusional He loss increasing from the centre to the rim of a grain, as illustrated with our modelled He profiles (e.g. Fig. 12). Measuring He in the centre of grains, as is common practice in in situ dating, leads to older ages than whole-grain dating. The latter includes diffusion-related He-depleted grain rims, yielding younger dates. Samples where the majority of produced He has not been affected by high diffusion rates have similar whole-grain and in situ dates, such as in the rapidly cooled Fish Canyon age standard (e.g. Horne et al., 2016; Pickering et al., 2020) or Ellendale pipe samples (Evans et al., 2015). In one additional scenario, whole-grain and in situ dates are anticipated to exhibit identical dates. This occurs with very large crystals irrespective of their specific cooling history, exemplified by Durango apatite and Madagascar monazite and zircon (see Boyce et al., 2006; Evans et al., 2015; Horne et al., 2019; Vermeesch et al., 2012).
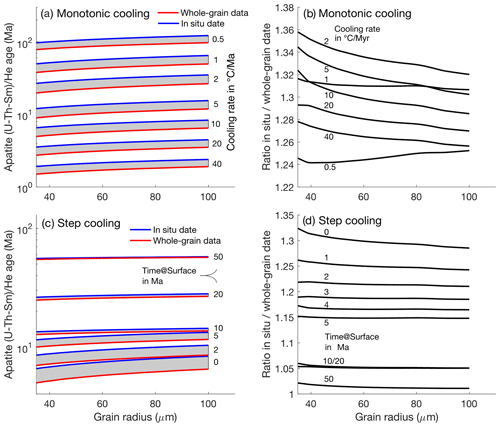
Figure 14Whole-grain vs. in situ (U–Th–Sm) He dates as a function of grain size and cooling rate for U, Th, and Sm concentrations of 10 ppm (homogenously distributed) and assuming a single-spot radius of 10 µm (2 µm deep) in the centre of a spherical grain. (a) Dates for cooling rates of 0.5 to 40 °C Myr−1. (b) Ratio of in situ and whole-grain dates as a function of grain size and cooling rate. (c–d) The same as (a) and (b) but modelled with a step cooling to surface temperature (10 °C) at different times (0–50 Ma) with a cooling rate of 10 °C Myr−1.
Tripathy-Lang et al. (2013) applied the in situ method to detrital zircons from a tributary of the Indus River in the Himalayas that drains the southern part of the Ladakh batholith. Cooling of the Ladakh batholith through the He partial retention zone for zircons likely occurred rapidly in Oligocene times (Kirstein et al., 2009). According to our modelling results, this should result in similar whole-grain and in situ zircon dates. In fact, the resulting whole-grain and in situ date distributions show comparable patterns, with slightly older whole-grain dates (mean date 29 vs. 26 Ma). Tripathy-Lang et al. (2013) interpreted the difference to result from preferential grain selection for whole-grain analyses and considered the in situ dates to be more representative. Alternatively, the larger spread and slight shift to older dates may be based on methodological differences, where in situ dates are generally older for samples that have experienced diffusional He loss.
In summary, in situ (U–Th–Sm) He dating of apatite or zircon is an alternative to whole-grain dating with obvious advantages. However, our modelling results demonstrate that dates cannot simply be interpreted together with whole-grain data. If analysed grains are expected to have lost a significant fraction of He by diffusion, in situ dates will be older than whole-grain dates. In the case of bedrock studies, in situ data can be interpreted using modified thermal models introduced here. To aid comparisons to existing whole-grain datasets, corresponding whole-grain data can be derived from those models. In most detrital studies, it is impossible to know the fractional loss of He of each individual grain, and in situ dates, if measured in the centre of grains, will be systematically older. In cases where the dates of source areas are greatly different (e.g. 15 vs. 30 vs. 90 Ma), inferences from in situ (U–Th–Sm) He dating might still be acceptable, such as in the detrital zircon study of the Inn River in the European Alps by Dunkl et al. (2024).
4.3 Grain selection considerations for in situ measurement
Grain selection for the in situ (U–Th–Sm) He method follows criteria similar to the whole-grain method. Simple 1D thermal history modelling requires that selected grains have smooth surfaces and are symmetrical, such as spheres and cylinders. The long prismatic shape and basal cleavage direction often result in the fragmentation of apatite grains, especially during the mineral separation process (e.g. Farley, 2002). Interpreting apatite fragments with the whole-grain and method usually requires corrections for grain fragmentation (e.g. Brown et al., 2013; Flowers and Farley, 2012). Instead, fragments of apatite grains broken along the basal faces can be treated similarly to intact grains with the in situ (U–Th–Sm) He method.
Grains should be free of inclusions to avoid excess He from long alpha-stopping distances (e.g. Farley, 2002). The pre-measurement exposure of the inner surface facilitates thorough inspection of the grain interior and identification of potential inclusions at sub-micrometre resolution using 1000× magnification. Even though it is not visually evident with microscopy, inclusions can be identified by measuring radionuclide concentrations with LA-ICP-MS. The downside of analysing inner surfaces after abrasion is that roughly half of the grain is not available for inspection, and thus outliers related to excess He from mineral inclusions (abraded away) will still be an issue in in situ (U–Th–Sm) He dating.
Similar to the whole-grain method, reliable date determination and thermal history reconstructions require precise measurements of grain geometries (e.g. Glotzbach et al., 2019). Future applications of the in situ (U–Th–Sm) He methodology will show whether geometry measurements are required before embedding grains or can be done within the mount following grain selection. Measurements of the distance between He laser pits and grain prism faces can follow pit volume measurements. An issue that may arise is the complexity involved in accurately determining the position of the inner surface relative to the original grain boundary, particularly in the vertical dimension of mounted grains. The common tetragonal and hexagonal cross-sectional shapes of zircons and apatites result in theoretically variably sized inner surfaces (e.g. Fig. 7). A symmetrical apatite and simple zircon grain have a ratio between circumradius to inner radius of and , respectively. It is therefore mandatory to accurately determine the correct location of the pit location with respect to the whole-grain geometry.
4.4 Recommended reporting procedure for in situ analytical data.
We recommend using the 1D modelling approach only for grains with homogeneous or concentric radionuclide distributions. The latter should be verified by spatially resolved or depth-resolved radionuclide information, e.g. with LA-ICP-MS depth profiling or mapping. Based on the model results presented here and the discussion in the previous section, we recommend reporting several different aspects of in situ measurements. These items will not only enable reproduction of dates for each spot but also facilitate modelling of grain thermal histories using the software of this study. Essential items to report in data tables for each grain include (1) grain geometry (preferably with photos in a supplementary file) and assumed grain geometry (e.g. sphere, infinite cylinder, other) used for age calculation; (2) (for each ablation pit across a grain) the pit diameter, measured volume, depth, and centre point of the pit relative to the a, b, and c axis of the grain; (3) the He measured from the ablation pit; (4) the U, Th, and Sm concentration profiles; (5) the calculated in situ grain date; and (6) the whole-grain equivalent date (which requires thermal history modelling; see Fig. 14). Reporting of the above information enables thermal history modelling of individual grains and comparison of in situ dates to whole-grain dates from neighbouring areas and/or previous studies.
4.5 Future considerations
Although the theoretical benefits and limitations have been explored here, more applications of the in situ (U–Th–Sm) He method to samples are required. Future studies should explore (i) the spatial relationship between radionuclide zoning and resulting He distribution and (ii) the reliability of in situ (U–Th–Sm) He-derived thermal history reconstructions. Lastly (iii), as previously mentioned, future modelling studies should evaluate tradeoffs between the cooling rate (particularly at higher cooling rates of > 10 °C Myr−1) and parent radionuclide concentrations to evaluate the limits of in situ dating in terms of producing geologically interpretable data.
This study examined the theoretical relationship between the parent radionuclide distribution and the resulting He concentrations within a grain (such as apatite or zircon). This was done using an updated version of the production, ejection, and diffusion model (i.e. RDAAM). We investigated the dependencies of predicted whole-grain and in situ apatite and zircon (U–Th–Sm) He dates for monotonic cooling histories (1–40 °C Myr−1), grain sizes (40–100 µm), and (in the case of in situ data) the position of the measurements within the grain. In addition, we explored strategies for reconstructing the thermal history from multiple and single apatite grains.
Model predictions revealed that the He concentration and resulting in situ date is mainly a function of the grain size, eU, and distance to the grain rim. Thus, the interpretation of in situ (U–Th–Sm) He dates necessitates the assessment of the grain geometry of the measured grains and determining the distance between the laser spot and the closest prismatic face. Most importantly, in situ dates for samples that experienced diffusional He loss will be older than whole-grain dates. In most cases, understanding in situ data necessitates the application of adapted thermal models such as those introduced in this study. Additionally, to facilitate a comparison to existing whole-grain data, corresponding whole-grain dates can be determined through thermal history modelling.
Our observations revealed that radionuclide zoning is not an anomaly but a prevalent occurrence in both apatite and zircon. Analysis of a substantial dataset using LA-ICP-MS for radionuclide measurements in these minerals demonstrated that the observed radionuclide zoning has, if disregarded, the potential to substantially skew the relationships between effective uranium (eU) and whole-grain dates. Furthermore, results suggest that a minimum of 10 apatite grains are needed to reach an R2 of 0.8 between eU and date and that a labour-intensive number (23) of whole-grain ZHe dates is needed to reach a minimum R2 of 0.5 between eU and date.
Two promising approaches exist for reconstructing the thermal history of rocks using the in situ (U–Th–Sm) He method. Similar to data obtained from whole grains, variations in grain size and/or effective uranium content, which lead to differences in helium diffusivity and in situ dates, can be utilized for thermal history reconstructions. The in situ (U–Th–Sm) He method can measure a He concentration profile in single grains, which is, among other factors, controlled by the cooling history. Modelling results suggest that several in situ (U–Th–Sm) He measurements along a profile from the centre of a grain to the prism face can be inverted to reconstruct the thermal history of a single grain.
The modified version of RDAAM and ZRDAAM code and MATLAB scripts to run these models are available from the Zenodo repository (https://doi.org/10.5281/zenodo.13898183, Glotzbach, 2024).
The data required to recalculate the stopping distances can be accessed through http://www.srim.org (last access: 15 November 2022), hosted by James F. Ziegler (Ziegler et al., 2010).
The supplement related to this article is available online at: https://doi.org/10.5194/gchron-6-697-2024-supplement.
Conceptualization: CG, TE. Formal analysis: CG. Investigation: CG. Methodology: CG. Software: CG. Visualization: CG. Writing: CG, TE.
The contact author has declared that neither of the authors has any competing interests.
Publisher’s note: Copernicus Publications remains neutral with regard to jurisdictional claims made in the text, published maps, institutional affiliations, or any other geographical representation in this paper. While Copernicus Publications makes every effort to include appropriate place names, the final responsibility lies with the authors.
The paper benefitted from discussions with Sarah Falkowski and Ann-Kathrin Maier and was improved through the thoughtful reviews of Istvan Dunkl and Rebecca Flowers and comments from Pieter Vermeesch. Klaus Mezger is thanked for editorial handling and technical corrections.
This study was supported by the Deutsche Forschungsgemeinschaft (DFG) to Christoph Glotzbach (GL 724/11-1) under the priority programme 4D-MB as a contribution to the AlpArray initiative, the Bundesgesellschaft für Endlagerung (BGE – STAFuE-21-12-Klei), and funding for large equipment from the DFG to Todd Ehlers (INST 37/1041-1 FUGG).
This paper was edited by Pieter Vermeesch and reviewed by István Dunkl and Rebecca Flowers.
Anderson, A. J., Hodges, K. V., and van Soest, M. C.: Empirical constraints on the effects of radiation damage on helium diffusion in zircon, Geochim. Cosmochim. Ac., 218, 308–322, https://doi.org/10.1016/j.gca.2017.09.006, 2017.
Boyce, J. W., Hodges, K. V., Olszewski, W. J., Jercinovic, M. J., Carpenter, B. D., and Reiners, P. W.: Laser microprobe (U–Th)/He geochronology, Geochim. Cosmochim. Ac., 70, 3031–3039. https://doi.org/10.1016/j.gca.2006.03.019, 2006.
Bragg, W. H., and Kleeman, R.: On the α particles of radium, and their loss of range in passing through various atoms and molecules, The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science, 10, 318–340, https://doi.org/10.1080/14786440509463378, 1905.
Brown, R. W., Beucher, R., Roper, S., Persano, C., Stuart, F., and Fitzgerald, P.: Natural age dispersion arising from the analysis of broken crystals. Part I: Theoretical basis and implications for the apatite (U–Th)/He thermochronometer, Geochim. Cosmochim. Ac., 122, 478–497, https://doi.org/10.1016/j.gca.2013.05.041, 2013.
Chew, D. M., Petrus, J. A., Kenny, G. G., and McEvoy, N.: Rapid high-resolution U–Pb LA-Q-ICPMS age mapping of zircon, J. Anal. Atom. Spectr., 32, 262–276, https://doi.org/10.1039/C6JA00404K, 2017.
Dunkl, I., Malis, F., Lünsdorf, N. K., Schönig, J., and Von Eynatten, H.: Zircon U-Pb-He Double Dating of Modern Sands From the Inn River Catchment: Assessing Resolution and Potential in a Complex Orogenic Setting, J. Geophys. Res.-Earth., 129, e2023JF007360, https://doi.org/10.1029/2023JF007360, 2024.
Ehlers, T. A.: Crustal Thermal Processes and the Interpretation of Thermochronometer Data, Rev. Mineral. Geochem., 58, 315–350, https://doi.org/10.2138/rmg.2005.58.12, 2005.
Ehlers, T. A. and Farley, K. A.: Apatite (U–Th)/He thermochronometry: methods and applications to problems in tectonic and surface processes, Earth Planet. Sc. Lett., 206, 1–14, https://doi.org/10.1016/S0012-821X(02)01069-5, 2003.
Evans, N. J., McInnes, B. I. A., McDonald, B., Danišík, M., Becker, T., Vermeesch, P., Shelley, M., Marillo-Sialer, E., and Patterson, D. B.: An in situ technique for (U–Th–Sm)/He and U–Pb double dating, J. Anal. Atom. Spectr., 30, 1636–1645, https://doi.org/10.1039/C5JA00085H, 2015.
Danišík, M., McInnes, B. I. A., Kirkland, C. L., McDonald, B. J., Evans, N. J., and Becker, T.: Seeing is believing: Visualization of He distribution in zircon and implications for thermal history reconstruction on single crystals, Sci. Adv., 3, e1601121, https://doi.org/10.1126/sciadv.1601121, 2017.
Falkowski, S., Ehlers, T. A., McQuarrie, N., Glover, C. O., Perez, N. D., and Buford Parks, V. M.: Exhumation and incision of the eastern Central Andes, southern Peru: Low-temperature thermochronology observations, Earth Planet. Sc. Lett., 620, 118299, https://doi.org/10.1016/j.epsl.2023.118299, 2023.
Farley, K. A.: Helium diffusion from apatite: General behavior as illustrated by Durango fluorapatite, J. Geophys. Res.-Sol. Ea., 105, 2903–2914, https://doi.org/10.1029/1999JB900348, 2000.
Farley, K. A.: (U-Th-Sm) He Dating: Techniques, Calibrations, and Applications, Rev. Mineral. Geochem., 47, 819–844, https://doi.org/10.2138/rmg.2002.47.18, 2002.
Farley, K. A., Wolf, R. A., and Silver, L. T.: The effects of long alpha-stopping distances on (U-Th-Sm) He dates, Geoch. Cosmochim. Ac., 60, 4223–4229, https://doi.org/10.1016/s0016-7037(96)00193-7, 1996.
Farley, K. A., Shuster, D. L., Watson, E. B., Wanser, K. H., and Balco, G.: Numerical investigations of apatite 4He/3He thermochronometry: APATITE 4He/3He THERMOCHRONOMETRY, Geochem. Geophy. Geosy., 11, Q10001, https://doi.org/10.1029/2010GC003243, 2010.
Farley, K. A., Shuster, D. L., and Ketcham, R. A.: U and Th zonation in apatite observed by laser ablation ICPMS, and implications for the (U–Th)/He system, Geochim. Cosmochim. Ac., 75, 4515–4530, https://doi.org/10.1016/j.gca.2011.05.020, 2011.
Flowers, R. M.: Exploiting radiation damage control on apatite (U–Th)/He dates in cratonic regions, Earth Planet. Sc. Lett., 277, 148–155, https://doi.org/10.1016/j.epsl.2008.10.005, 2009.
Flowers, R. M. and Farley, K. A.: Apatite 4He/3He and (U-Th)/He Evidence for an Ancient Grand Canyon, Science, 338, 1616–1619, https://doi.org/10.1126/science.1229390, 2012.
Flowers, R. M., Ketcham, R. A., Shuster, D. L., and Farley, K. A.: Apatite (U–Th)/He thermochronometry using a radiation damage accumulation and annealing model, Geochim. Cosmochim. Ac., 73, 2347–2365, https://doi.org/10.1016/j.gca.2009.01.015, 2009.
Flowers, R. M., Ketcham, R. A., Enkelmann, E., Gautheron, C., Reiners, P. W., Metcalf, J. R., Danišík, M., Stockli, D. F., and Brown, R. W.: (U-Th)/He chronology: Part 2. Considerations for evaluating, integrating, and interpreting conventional individual aliquot data, GSA Bull., 132, 137–161, https://doi.org/10.1130/B36268.1, 2023.
Fox, M., McKeon, R. E., and Shuster, D. L.: Incorporating 3-D parent nuclide zonation for apatite 4He/3He thermochronometry: An example from the Appalachian Mountains, Geochem. Geophy. Geosy., 15, 4217–4229, https://doi.org/10.1002/2014GC005464, 2014.
Fox, M., Tripathy-Lang, A., and Shuster, D. L.: Improved spatial resolution of elemental maps through inversion of LA-ICP-MS data, Chem. Geol., 467, 30–41, https://doi.org/10.1016/j.chemgeo.2017.07.001, 2017.
Gallagher, K., Brown, R., and Johnson, C.: Fission track analysis and its applications to geological problems, Ann. Rev. Earth Planet. Sci., 26, 519–572, https://doi.org/10.1146/annurev.earth.26.1.519, 1998.
Gautheron, C., Tassan-Got, L., Barbarand, J., and Pagel, M.: Effect of alpha-damage annealing on apatite (U–Th)/He thermochronology, Chem. Geol., 266, 157–170, https://doi.org/10.1016/j.chemgeo.2009.06.001, 2009.
Gautheron, C., Tassan-Got, L., Ketcham, R. A., and Dobson, K. J.: Accounting for long alpha-particle stopping distances in (U–Th–Sm)/He geochronology: 3D modeling of diffusion, zoning, implantation, and abrasion, Geochim. Cosmochim. Ac., 96, 44–56, https://doi.org/10.1016/j.gca.2012.08.016, 2012.
Glotzbach, C.: Interpreting cooling dates and histories from laser ablation in-situ (U-Th-Sm)/He thermochronometry, Zenodo [code], https://doi.org/10.5281/zenodo.13898183, 2024.
Glotzbach, C., Lang, K. A., Avdievitch, N. N., and Ehlers, T. A.: Increasing the accuracy of (U-Th(-Sm))/He dating with 3D grain modelling, Chem. Geol., 506, 113–125, https://doi.org/10.1016/j.chemgeo.2018.12.032, 2019.
Guenthner, W. R., Reiners, P. W., Ketcham, R. A., Nasdala, L., and Giester, G.: Helium diffusion in natural zircon: Radiation damage, anisotropy, and the interpretation of zircon (U-Th-Sm) He thermochronology, Am. J. Sci., 313, 145–198, https://doi.org/10.2475/03.2013.01, 2013.
Guenthner, W. R., Reiners, P. W., Drake, H., and Tillberg, M.: Zircon, titanite, and apatite (U-Th-Sm) He dates and date-eU correlations from the Fennoscandian Shield, southern Sweden: Fennoscandian Zirc He Date-eU Correlation, Tectonics, 36, 1254–1274, https://doi.org/10.1002/2017TC004525, 2017.
Horne, A. M., van Soest, M. C., Hodges, K. V., Tripathy-Lang, A., and Hourigan, J. K.: Integrated single crystal laser ablation U/Pb and (U–Th)/He dating of detrital accessory minerals – Proof-of-concept studies of titanites and zircons from the Fish Canyon tuff, Geochim. Cosmochim. Ac., 178, 106–123, https://doi.org/10.1016/j.gca.2015.11.044, 2016.
Horne, A. M., van Soest, M. C., and Hodges, K. V.: U/Pb and (U-Th-Sm) He “double” dating of detrital apatite by laser ablation: A critical evaluation, Chem. Geol., 506, 40–50, https://doi.org/10.1016/j.chemgeo.2018.12.004, 2019.
Hourigan, J. K., Reiners, P. W., and Brandon, M. T.: U-Th zonation-dependent alpha-ejection in (U-Th)/He chronometry, Geochim. Cosmochim. Ac., 69, 3349–3365, https://doi.org/10.1016/j.gca.2005.01.024, 2005.
Ketcham, R. A.: Forward and Inverse Modeling of Low-Temperature Thermochronometry Data, Rev. Mineral. Geochem., 58, 275–314, https://doi.org/10.2138/rmg.2005.58.11, 2005.
Ketcham, R. A., Gautheron, C., and Tassan-Got, L.: Accounting for long alpha-particle stopping distances in (U–Th–Sm)/He geochronology: Refinement of the baseline case, Geochim. Cosmochim. Ac., 75, 7779–7791, https://doi.org/10.1016/j.gca.2011.10.011, 2011.
Kirstein, L. A., Foeken, J. P. T., van der Beek, P., Stuart, F. M., and Phillips, R. J.: Cenozoic unroofing history of the Ladakh Batholith, western Himalaya, constrained by thermochronology and numerical modelling, J. Geol. Soc., 166, 667–678, https://doi.org/10.1144/0016-76492008-107, 2009.
Lippolt, H. J., Leitz, M., Wernicke, R. S., and Hagedorn, B.: (Uranium + thorium)/helium dating of apatite: experience with samples from different geochemical environments, Chem. Geol., 112, 179–191, https://doi.org/10.1016/0009-2541(94)90113-9, 1994.
Malusà, M. G. and Fitzgerald, P. G. (Eds.): Fission-track thermochronology and its application to geology, Springer, 393 pp., https://doi.org/10.1007/978-3-319-89421-8, 2019.
Meesters, A. G. C. A., and Dunai, T. J.: Solving the production–diffusion equation for finite diffusion domains of various shapes, Chem. Geol., 186, 333–344, https://doi.org/10.1016/S0009-2541(01)00422-3, 2002.
North, R., White, L. T., Nancarrow, M., Dosseto, A., and Tanner, D.: Sub-Micrometre Resolution FIB-SEM-based ToF-SIMS Used to Map Geochemical Zoning in Four Zircon Reference Materials, Geostand. Geoanal. Res., 47, 125–142, https://doi.org/10.1111/ggr.12463, 2023.
Paton, C., Woodhead, J. D., Hellstrom, J. C., Hergt, J. M., Greig, A., and Maas, R.: Improved laser ablation U‐Pb zircon geochronology through robust downhole fractionation correction, Geochem. Geophys. Geosy., 11, Q0AA06, https://doi.org/10.1029/2009GC002618, 2010.
Pickering, J., Matthews, W., Enkelmann, E., Guest, B., Sykes, C., and Koblinger, B. M.: Laser ablation (U-Th-Sm) He dating of detrital apatite, Chem. Geol., 548, 119683, https://doi.org/10.1016/j.chemgeo.2020.119683, 2020.
Reiners, P. W.: Zircon (U-Th-Sm) He Thermochronometry, Rev. Mineral Geochem., 58, 151–179, https://doi.org/10.2138/rmg.2005.58.6, 2005.
Reiners, P. W. and Ehlers, T. A.: Low-temperature thermochronology: Techniques, interpretations and applications, Rev. Mineral. Geochem., 58, https://doi.org/10.2138/rmg.2005.58.0, 2005.
Reiners, P. W. and Brandon, M. T.: Using thermochronology to understand orogenic erosion, Annu. Rev. Earth Pl. Sci., 34, 419–466, https://doi.org/10.1146/annurev.earth.34.031405.125202, 2006.
Shuster, D. L. and Farley, K. A.: 4He/3He thermochronometry, Earth Planet. Sc. Lett., 217, 1–17, https://doi.org/10.1016/S0012-821X(03)00595-8, 2004.
Sousa, F. J., Cox, S. E., Rasbury, E. T., Hemming, S. R., Lanzirotti, A., and Newville, M.: U and Th zonation in apatite observed by synchrotron X-ray fluorescence tomography and implications for the (U–Th)/He system, Geochronology, 6, 553–570, https://doi.org/10.5194/gchron-6-553-2024, 2024.
Spiegel, C., Kohn, B., Belton, D., Berner, Z., and Gleadow, A.: Apatite (U–Th–Sm)/He thermochronology of rapidly cooled samples: The effect of He implantation, Earth Planet. Sc. Lett., 285, 105–114, https://doi.org/10.1016/j.epsl.2009.05.045, 2009.
Tripathy-Lang, A., Hodges, K. V., Monteleone, B. D., and van Soest, M. C.: Laser (U-Th)/He thermochronology of detrital zircons as a tool for studying surface processes in modern catchments, J. Geophys. Res.-Earth, 118, 1333–1341. https://doi.org/10.1002/jgrf.20091, 2013.
Vermeesch, P., Seward, D., Latkoczy, C., Wipf, M., Günther, D., and Baur, H.: α-Emitting mineral inclusions in apatite, their effect on (U–Th)/He dates, and how to reduce it, Geochim. Cosmochim. Ac., 71, 1737–1746, https://doi.org/10.1016/j.gca.2006.09.020, 2007.
Vermeesch, P., Sherlock, S. C., Roberts, N. M. W., and Carter, A.: A simple method for in-situ U–Th–He dating, Geochim. Cosmochim. Ac., 79, 140–147, https://doi.org/10.1016/j.gca.2011.11.042, 2012.
Vermeesch, P., Tian, Y., Schwanethal, J., and Buret, Y.: Technical note: In situ U–Th–He dating by 4He/3He laser microprobe analysis, Geochronology, 5, 323–332, https://doi.org/10.5194/gchron-5-323-2023, 2023.
Wolf, R. A., Farley, K. A., and Silver, L. T.: Helium diffusion and low-temperature thermochronometry of apatite, Geochim. Cosmochim. Ac., 60, 4231–4240, https://doi.org/10.1016/s0016-7037(96)00192-5, 1996.
Wolf, R. A., Farley, K. A., and Kass, D. M.: Modeling of the temperature sensitivity of the apatite (U–Th)/He thermochronometer, Chem. Geol., 148, 105–114, https://doi.org/10.1016/S0009-2541(98)00024-2, 1998.
Ziegler, J. F., Ziegler, M. D., and Biersack, J. P.: SRIM – The stopping and range of ions in matter (2010), Nucl. Instrum. Methods B, 268, 1818–1823, https://doi.org/10.1016/j.nimb.2010.02.091, 2010.





