Accuracy and validity of maximum depositional ages in light of tandem (laser ablation and isotope dilution) U–Pb detrital zircon geochronology, including results from northern Alaska

Sound geologic reasoning underpins detrital zircon (DZ) maximum depositional ages (MDAs) via the principle of inclusions, although interpreting in situ U–Pb date distributions requires many geologically, analytically, and statistically driven decisions. Existing research highlights strengths and challenges of various algorithm approaches to deriving MDAs from DZ dates, yet community consensus on best practices remains elusive. Here, we first address new laser ablation–inductively coupled plasma mass spectrometry (LA-ICPMS) and chemical abrasion–isotope dilution–thermal ionization mass spectrometry (CA-ID-TIMS) U–Pb geochronology for five DZ samples from a ∼1 km thick section of mid-Cretaceous strata in Alaska's Colville foreland basin. Youthful DZ yields are extremely sparse, and the MDAs are n=1. LA-ICPMS and CA-ID-TIMS dates from the same grains (i.e., tandem dating) adhere to a uniform pattern: laser ablation dates are younger than paired isotope dilution dates, with in situ offsets ranging from −0.3 % to −6.4 %. Existing biostratigraphic constraints suggest a ∼110–94 Ma sedimentation window for the sampled section, but the CA-ID-TIMS MDAs reduce by ∼8.5 Myr the maximum geologic time recorded by the stratigraphy. A simple age–depth analysis incorporating the CA-ID-TIMS MDAs and correlation of a new CA-ID-TIMS tephra zircon age yields geologically reasonable minimum stratigraphic accumulation rates, but an LA-ICPMS-based interpretation would render an improbable and inaccurate chronostratigraphy. We then explore the new tandem data and two previously published Mesozoic tandem DZ datasets for their broader MDA research implications, focusing on tandem-date pair relations and youthful-population sampling densities rather than conducting the typical MDA algorithm output assessment. Percent-offset plots document impactful (∼2 %–3 % on average) and pervasive (∼87 %–100 % of pairs per study) young bias for the laser ablation dates, likely reflecting a complex combination of analytical dispersion, low-temperature Pb loss, and matrix effects, which are topics we review in detail. Deconvolving offset sources without elaborate geochronologic experiments is difficult, but our tandem-date analysis provides critical context, and follow-up CA-ID-TIMS can diminish or eliminate analytical, systematic, and geologic offset sources. We also (1) redefine the reference value for MDA accuracy as the crystallization age of the youngest analyzed DZ population in a sample and (2) reframe LA-ICPMS-based DZ MDA algorithm evaluations around validity – how capable are the metrics of accurately measuring what they are intended to measure? – rather than MDA benchmarking by existing age constraints. These new perspectives follow straightforward geochronologic and stratigraphic principles, and our synthesis intends to identify and clarify opportunities to further refine DZ MDA research.

1 Introduction

The principle of inclusions establishes that a sedimentary rock cannot be older than its youngest zircon (Houston and Murphy, 1965; Fedo et al., 2003). Zircon that crystallizes shortly before eruption or exhumation and is then transported and deposited as detritus in a sedimentary basin can yield a near-stratal-age U–Pb maximum depositional age (MDA) (e.g., Gehrels, 2014; Coutts et al., 2019; Sharman and Malkowski, 2020). Detrital zircon (DZ) MDAs are now an essential tool of chronostratigraphy (e.g., Daniels et al., 2018; Karlstrom et al., 2018, 2020; Landing et al., 2021; Cothren et al., 2022; Huang et al., 2022; Lease et al., 2022; Dehler et al., 2023; Coutts et al., 2024), and numerous recent papers present insights into this method (e.g., Coutts et al., 2019; Herriott et al., 2019a; Johnstone et al., 2019; Rossignol et al., 2019; Copeland, 2020; Gehrels et al., 2020; Sharman and Malkowski, 2020; Finzel and Rosenblume, 2021; Rasmussen et al., 2021; Vermeesch, 2021; Isakson et al., 2022; Schwartz et al., 2023; Sundell et al., 2024). These efforts build on the foundational DZ MDA study by Dickinson and Gehrels (2009) and highlight the need to carefully consider sampling protocols, experimental designs, data filtering, uncertainty sources and handling, and statistical assessments and modeling (e.g., Sharman and Malkowski, 2020).

The proliferation of algorithms used to derive MDAs is a conspicuous aspect of the DZ literature (see, e.g., Coutts et al., 2019; Copeland, 2020; Sharman and Malkowski, 2020; Vermeesch, 2021; Sundell et al., 2024). When DZ samples yield abundant youthful (i.e., near-stratal/depositional-age) U–Pb dates, a researcher has numerous interpretive metrics to choose from and will make the first-order decision of whether to establish MDAs with a single zircon or multiple zircon grains. Some authors note apparent benefits of statistically assessing the distribution of youthful DZ dates in deriving multi-grain MDAs (e.g., Herriott et al., 2019a; Vermeesch, 2021), whereas others cite geologic limitations (e.g., unknown provenance or magmatic relations) to pooling detrital dates and recommend single-grain MDAs regardless of youthful-population yields (e.g., Spencer et al., 2016; Copeland, 2020). Arguments and demonstrations from the single-grain and multi-grain MDA perspectives have not yet yielded consensus (see Sharman and Malkowski, 2020; Sundell et al., 2024), and the youngest single grain (YSG) and youngest grain cluster with overlap at 2σ (YC2σ) algorithms of Dickinson and Gehrels (2009) are two of the most highly utilized metrics in DZ case studies (Coutts et al., 2019).

Laser ablation–inductively coupled plasma mass spectrometry (LA-ICPMS) is the most common method for DZ U–Pb geochronology, yet analytical, systematic, and geologic uncertainties can undermine the accuracy of MDAs from LA-ICPMS (e.g., Herriott et al., 2019a). The MDA algorithms were established for and mainly applied to LA-ICPMS DZ dates with the general aim to accommodate varying youthful zircon yields and random, systematic, and geologic errors related to analytical dispersion, matrix effects, and Pb loss that can bias measured dates from true crystallization ages. Analytical dispersion is the most easily understood of these uncertainties and is ideally well characterized by laboratories, yet a typical ±2 %–4 % (2σ) analytical uncertainty for LA-ICPMS dates can mask geologic relations and processes of interest (e.g., Klein and Eddy, 2024). Matrix effects, or variable ablation behavior among natural reference zircon (e.g., Temora-2) and unknowns (e.g., sampled DZ), are perhaps an underappreciated and under-characterized source of uncertainty in LA-ICPMS zircon geochronology (e.g., Klötzli et al., 2009; Allen and Campbell, 2012; Sliwinski et al., 2017; Ver Hoeve et al., 2018). Furthermore, Pb loss in DZ – which is difficult or impossible to recognize in LA-ICPMS dates for Meso-Cenozoic zircon (e.g., Spencer et al., 2016) – is more likely pervasive (Keller et al., 2019; Rasmussen et al., 2021; Isakson et al., 2022; Howard et al., 2025; also Sharman and Malkowski, 2024) than negligible (Copeland, 2020; Vermeesch, 2021).

U–Pb zircon dating is a premier radioisotopic geochronometer, with chemical abrasion–isotope dilution–thermal ionization mass spectrometry (CA-ID-TIMS; Mattinson, 2005) providing high precision and accuracy in deep time (e.g., Schmitz et al., 2020; Schaltegger et al., 2021; Condon et al., 2024). Relatively rapid in situ microbeam geochronology by secondary ionization mass spectrometry (SIMS) and then LA-ICPMS revolutionized the field of DZ research (Gehrels, 2012). In recent years CA-ID-TIMS has been introduced in tandem, multi-mass-spectrometry experimental design workflows for DZ studies to establish precise and accurate MDAs (e.g., Macdonald et al., 2014; Burgess and Bowring, 2015; Eddy et al., 2016; Karlstrom et al., 2018, 2020; Herriott et al., 2019a; Landing et al., 2021; Rasmussen et al., 2021; Isakson et al., 2022), leveraging the benefits of both in situ and isotope dilution techniques (e.g., Mattinson, 2013; Schaltegger et al., 2015). CA-ID-TIMS alleviates or dispenses with many of the current challenges for LA-ICPMS by (1) improved analytical resolution (e.g., $\sim \mathrm{50}\times$) through highly sensitive and stable mass spectrometry; (2) removal of matrix-effect uncertainties through isotope dilution analysis with a well-calibrated tracer solution; (3) accurate correction for initial common Pb using precisely measured ${}^{\mathrm{206}}\mathrm{Pb}{/}^{\mathrm{204}}\mathrm{Pb}$ ratios; and (4) pre-treatment with the chemical abrasion protocol, which is the most successful approach for mitigating Pb loss from zircon (e.g., Schoene, 2014; Schaltegger et al., 2015).

Regardless of what preference a researcher may have for single- or multi-grain MDAs, if very few youthful DZs are identified in a sample, there are likely limited options (e.g., a single-grain MDA or no MDA at all). Within this context, we present n=1 (grain) DZ MDAs from mid-Cretaceous foreland basin strata of northern Alaska with sparse youthful zircon yields. A tephra zircon sample from a key locality that exposes a correlative cap of the studied section provides minimum, overlying age constraints. This study employs LA-ICPMS and CA-ID-TIMS U–Pb geochronology of the same zircon crystals (i.e., tandem dating) to establish a new chronostratigraphic framework for the Torok and Nanushuk formations at Slope Mountain. An assessment of these new low-n youthful-population tandem DZ data (see data release by Herriott et al., 2024) and two previously published, higher-n youthful-population tandem DZ datasets (Herriott et al., 2019a; Rasmussen et al., 2021) places new focus on laser ablation date offsets rather than MDA derivations in order to gain novel insights. We present a review of candidate offset sources that can render LA-ICPMS-based MDAs with young bias. Our synthesis provides opportunity to evaluate current trends and future directions for DZ MDA studies.

2 Northern Alaska case study

2.1 Geologic background

The Colville foreland basin of northern Alaska formed in response to an initial phase of Late Jurassic–Early Cretaceous Brookian orogenesis (e.g., Moore et al., 1994; Houseknecht, 2019a). The Torok and Nanushuk formations record an Aptian–Cenomanian cycle of Brookian sedimentation, building a large clinothem (e.g., Houseknecht, 2019b; Fig. 1a). Time-transgressive progradation of coupled Nanushuk (non-marine and shallow-marine topsets) and Torok (deep-marine slope foresets and proximal basin-floor bottomsets) depositional systems principally progressed longitudinally from west to east, with an additional component of transverse sediment supply and associated clinothem growth from the Brooks Range to the south (e.g., Bird and Molenaar, 1992; Houseknecht et al., 2009; Houseknecht, 2019a, b; Lease et al., 2022).

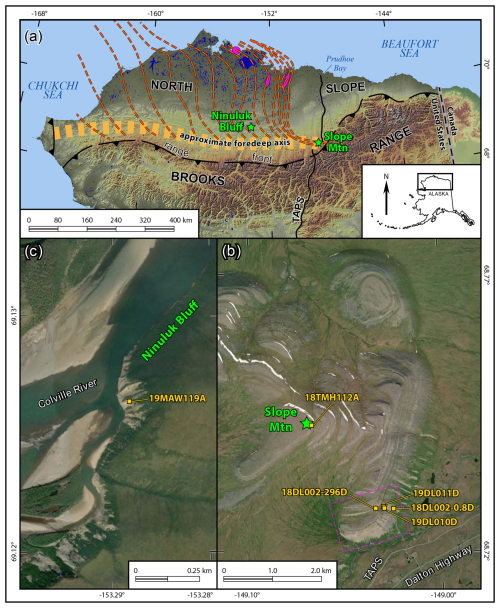
Figure 1 Location map of northern Alaska (a) and the Slope Mountain (b) and Ninuluk Bluff (c) sample localities. Nanushuk–Torok clinothem paleo-shelf margins (dashed orange lines) and recent clinothem-related oil discoveries (magenta ovals) are from Houseknecht (2019b); approximate foredeep axis is from Houseknecht et al. (2009; see Decker, 2007, for range-front structures). Note that the detrital zircon maximum depositional ages of Lease et al. (2022) are mainly tied to basin-axial depositional systems associated with approximately north–south-trending segments of Nanushuk–Torok paleo-shelf margins across the central and western North Slope and Chukchi Sea between the approximate latitudes of Ninuluk Bluff (∼69° N) and the coast to the north (∼71° N), as well as deep-water, basin-floor equivalents to the northeast of Slope Mountain. The dashed magenta line in (b) delineates the area visible in Fig. 6a. Imagery from the National Elevation Data Set, United States Geological Survey (a), and Maxar Technologies Inc., Alaska Geospatial Office, United States Geological Survey (b, c). Mtn – Mountain; TAPS – Trans-Alaska Pipeline System.

Our new chronostratigraphic work focuses on an exposure at Slope Mountain (Fig. 1), where uppermost Torok of near-shelf-edge affinity crops out beneath a ∼1 km thick succession of shallow-marine, non-marine, and, again, shallow-marine Nanushuk (e.g., Keller et al., 1961; Huffman et al., 1981; Huffman, 1985; Schenk and Bird, 1993; Johnsson and Sokol, 2000; Harris et al., 2002; LePain et al., 2009, 2022; Herriott et al., 2024; Fig. 2). LePain et al. (2022) noted the economic relevance of the lower Nanushuk at Slope Mountain, where shoreface and delta-front deposits can serve as outcrop analogs for a major oil exploration fairway to the northwest (Houseknecht, 2019b; also Fig. 1a). A prominent unconformity lies within the ∼500 m thick lower Nanushuk marine stratigraphy at ∼144 m above the Torok–Nanushuk contact (LePain et al., 2022) and has been interpreted as an incised valley (Schenk and Bird, 1993; LePain et al., 2009). A ∼400 m thick non-marine section in Nanushuk (Fig. 2) reflects continued (northward) shoreline regression associated with Nanushuk–Torok depositional systems, although there are no known Nanushuk outcrops north of Slope Mountain.

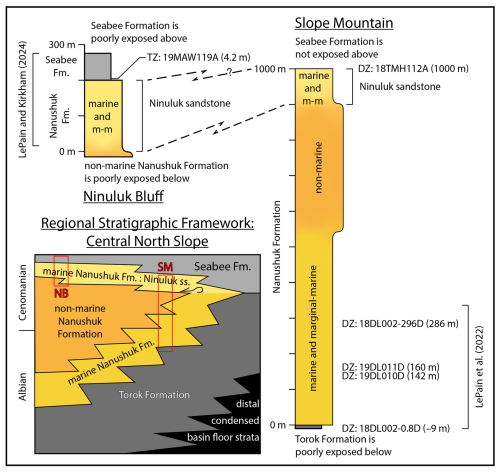
Figure 2 Stratigraphic relations and correlations of the Slope Mountain and Ninuluk Bluff sections. See text for discussion of the studied stratigraphy; see Tables 1 and 2 and Herriott et al. (2024) for sample details. Note that the lower Seabee Formation at Ninuluk Bluff is associated with offshore sedimentation (LePain et al., 2009; LePain and Kirkham, 2024). The regional framework is adapted from Houseknecht (2019b); the Ninuluk Bluff section is adapted from Detterman et al. (1963), LePain et al. (2009), and LePain and Kirkham (2024); the Slope Mountain section is adapted from Johnsson and Sokol (2000) and LePain et al. (2009, 2022) (see also Herriott et al., 2024). DZ – detrital zircon; Fm – Formation; m-m – marginal-marine; NB – Ninuluk Bluff; SM – Slope Mountain; TZ – tephra zircon.

The ∼100 m thick upper succession of marine Nanushuk at Slope Mountain is regionally correlated with the Ninuluk sandstone (Fig. 2), which is a top-of-Nanushuk transgressive unit (Houseknecht and Schenk, 2005; LePain et al., 2009) best known from its exposure at Ninuluk Bluff (Detterman et al., 1963; LePain and Kirkham, 2024; Fig. 1). Regionally, the Nanushuk and Torok are overlain by the Seabee Formation (e.g., Mull et al., 2003; Houseknecht, 2019a), although exposures of the transition are rare, and Seabee does not crop out at Slope Mountain. At localities where the Nanushuk–Seabee contact is exposed (e.g., Ninuluk Bluff), the Ninuluk sandstone is locally recognized and abruptly capped by a transgressive surface of erosion that is overlain by offshore deposits of the lower Seabee Formation (e.g., LePain et al., 2009; LePain and Kirkham, 2024; see also LePain et al., 2021). The Ninuluk sandstone and lower Seabee are collectively interpreted as a major low-frequency (e.g., third-order) transgressive systems tract (Houseknecht and Schenk, 2005; Lease et al., 2022), although higher-frequency forced regressions are reflected in the retrogradationally stacked Ninuluk sandstone section at Ninuluk Bluff (LePain et al., 2009; LePain and Kirkham, 2024).

Ammonites, pelecypods, palynomorphs, and foraminifera from the Nanushuk outcrop trend of the central North Slope that extends between Slope Mountain and Ninuluk Bluff (Fig. 1) are interpreted to be as old as earliest middle Albian (e.g., Keller et al., 1961; Reifenstuhl and Plumb, 1993; Mull et al., 2003; LePain et al., 2009), which corresponds to ∼110 Ma (see Gale et al., 2020). The Ninuluk sandstone is generally recognized as a Cenomanian unit based on the presence of Inoceramus dunveganensis (e.g., Jones and Gryc, 1960; Keller et al., 1961; Detterman et al., 1963; LePain et al., 2009). The lower Seabee Formation regionally bears Turonian ammonites and pelecypods and microfossils (e.g., Jones and Gryc, 1960; Detterman et al., 1963; Mull et al., 2003); however, some K–Ar and ${}^{\mathrm{40}}\mathrm{Ar}{/}^{\mathrm{39}}\mathrm{Ar}$ dates from tephra deposits equivocally suggest early (Shimer et al., 2016) to perhaps late (Lanphere and Tailleur, 1983; Mull et al., 2003) Cenomanian timing for the onset of Seabee sedimentation. Current constraints for the Albian–Cenomanian and Cenomanian–Turonian transitions are 100.5±0.1 and 93.9±0.2 Ma, respectively (Cohen et al., 2013; 2σ uncertainties from Gale et al., 2020).

Lease et al. (2022) presented LA-ICPMS-based DZ MDAs for the Nanushuk–Torok clinothem along a ∼800 km long, basin-axial transect, with lower (and time-transgressively older) Nanushuk in the far west (Chukchi Sea area; Fig. 1) being no older than ∼115 Ma. Those authors also reported four ∼95 Ma DZ MDAs from Ninuluk sandstone samples that were interpreted to indicate apparently synchronous transgressive termination of the long-lived clinothem. Note that Slope Mountain lies south and east of the main approximately north–south-trending segments of Nanushuk–Torok paleo-shelf margins that Lease et al. (2022) focused on (see also Fig. 1). And the Slope Mountain stratigraphy is associated with relatively tightly spaced, approximately east–west-trending paleo-shelf margins that advanced northward from the ancestral Brooks Range in a paleogeographic position dominated by transverse sediment routing systems (e.g., Houseknecht et al., 2009; Houseknecht, 2019b; Fig. 1). Ultimately, time-transgressive sedimentation of lithostratigraphic and seismic stratigraphic units, architectural-fill complexities tied to axial versus transverse sediment routing, subsequent fold-and-thrust-belt deformation, and limited seismic stratigraphic resolution along the southern basin margin preclude extrapolating a maximum age constraint for the Torok–Nanushuk contact at Slope Mountain from the clinothem's DZ MDA-based chronostratigraphic framework of Lease et al. (2022). Current constraints do, however, suggest that the Ninuluk sandstone at the top of the Nanushuk Formation at Slope Mountain is associated with the aforementioned transgressive cessation of Nanushuk–Torok depositional systems during late Cenomanian time at $\sim \le \mathrm{95}$ Ma. Thus, existing biostratigraphic and geochronologic information suggests the studied stratigraphy at Slope Mountain is ∼110–94 Ma.

2.2 Methods

We sampled one sandstone from the uppermost Torok Formation and four sandstones from the Nanushuk Formation at Slope Mountain (Figs. 1b and 2). Stratigraphic context and positions for the lower Nanushuk samples are keyed into the work by LePain et al. (2022). Sample 18TMH112A was collected from Nanushuk at the top of the exposed stratigraphy at Slope Mountain and assigned a stratigraphic position of 1000 m above the Torok–Nanushuk contact (Johnsson and Sokol, 2000; Herriott et al., 2024). We also collected a Seabee Formation air-fall tephra deposit sample from 4.2 m above the Nanushuk Formation at Ninuluk Bluff (Figs. 1a and 2; Table 2; Herriott et al., 2024; LePain and Kirkham, 2024). Additional information for these samples is included in a companion data-release report by Herriott et al. (2024).

All samples were prepared and analyzed at Boise State University's Isotope Geology Laboratory. For the detrital samples, we planned to date an unbiased selection of ∼200 grains per sample by LA-ICPMS. Samples typically comprised ∼1–2 kg of sandstone. Two sample bags of 18TMH112A were originally collected, and the second bag was analyzed in a later session (see Herriott et al., 2024), with a shifted focus toward smaller zircon of possible air-fall origin. Zircon yields and spot placement considerations resulted in dating 60–229 zircons per sample by LA-ICPMS (Table 1), and mid-Cretaceous zircons as identified by LA-ICPMS were plucked from their epoxy mounts, broken into fragments for multiple analyses if practical, and analyzed by CA-ID-TIMS. Fourteen zircon crystals from the Ninuluk Bluff tephra deposit were dated by LA-ICPMS, and six crystals were selected, plucked, and analyzed by CA-ID-TIMS (Table 2); follow-up selection criteria for these tephra zircon included LA-ICPMS date (i.e., a mid-Cretaceous result); grain morphology – e.g., favoring sharply faceted, commonly elongate crystals consistent with air-fall origin and limited re-working; and presence of melt inclusions suggestive of late-stage, rapid crystallization. Detailed methods, analytical results, metadata, and cathodoluminescence images of the analyzed zircon are archived by Herriott et al. (2024).

2.2.1 Uncertainty handling and reporting

The uncertainty reporting framework established for ID-TIMS data (Schoene et al., 2006) has been adapted or adopted for LA-ICPMS data as well (e.g., Schoene, 2014; Horstwood et al., 2016; Condon et al., 2024). All U–Pb zircon dates from this study and re-examined from the literature are presented, discussed, and interpreted at 2σ. For the new LA-ICPMS and CA-ID-TIMS data, uncertainties are noted in the format of ± X (Y) [Z], where X is internal/random/analytical uncertainty, Y is internal with reference (i.e., “standard”) zircon (LA-ICPMS) or tracer (CA-ID-TIMS) calibration uncertainty, and Z is internal with standard or tracer and U–Pb decay constant uncertainties (Schoene et al., 2006; also Schoene, 2014; Schaltegger et al., 2015). Studies that handle LA-ICPMS uncertainties in the format proposed by Horstwood et al. (2016) are designated as ± X [Z], where X is internal/random/analytical uncertainty and Z is internal with the quantified systematic uncertainties (standard calibration or long-term excess variance, decay constant, etc.). It is generally viewed as appropriate to compare (1) within-session data (LA-ICPMS) or data with the same tracer (CA-ID-TIMS) to each other at X, (2) the same geochronometer (e.g., U–Pb zircon) data at Y, and (3) any inter-geochronometer or disparate chronostratigraphic data type at Z (e.g., Schoene, 2014).

2.2.2 MDAs, ages, offset relations, and terms

The DZ MDAs from Slope Mountain are based on single-grain CA-ID-TIMS results. MDAs for youthful DZ that were broken into fragments and dated separately by CA-ID-TIMS are reported as weighted means of the crystal fragment dates that overlap at ±2σ analytical uncertainty and have a probability of fit >0.05. A stratal age for the Ninuluk Bluff tephra zircon sample is based on a weighted mean of the CA-ID-TIMS dates that overlap at ±2σ analytical uncertainty and yield a probability of fit >0.05. The >0.05 probabilities of fit cut-offs permit date dispersion to range as widely as is statistically permissible for a single population in a ∼95 % probability context for the number of analyses (n) in the weighted mean (e.g., Spencer et al., 2016). MDA algorithms discussed below are always tied to LA-ICPMS data, reflecting their usage in the DZ literature.

Tandem, or paired, U–Pb dates always refer to LA-ICPMS and CA-ID-TIMS results from the same zircon crystal. Some of the tandem-date comparisons herein are between multiple-analysis, weighted-mean results (probability of fit >0.05) of the LA-ICPMS data, the CA-ID-TIMS data, or both. For LA-ICPMS, multiple analyses mean multiple laser ablation spots placed on the same grain; for CA-ID-TIMS, multiple analyses mean that multiple crystal fragments derived from the same grain were dated separately (e.g., Herriott et al., 2019a). For a single pair of tandem dates, quantified offsets are based on the LA-ICPMS date relative to the CA-ID-TIMS date: $\text{offset}\left(\mathit{\%}\right)=\mathrm{100}\cdot (\text{LA-ICPMS date}-\text{CA-ID-TIMS date})/\left(\text{CA-ID-TIMS date}\right)$ and $\text{offset}\left(\mathrm{Myr}\right)=\text{LA-ICPMS date}-\text{CA-ID-TIMS date}$. In this framework, CA-ID-TIMS sets the benchmark (i.e., reference value; e.g., Horstwood et al., 2016), and a young bias for an LA-ICPMS result is always a negative value.

Two additional metrologic terms are also employed herein, generally following Schoene et al. (2013), Horstwood et al. (2016), and Reiners et al. (2017): (1) precision characterizes data dispersion, repeatability, and reproducibility and typically constitutes reported uncertainties (at X) at a given confidence level (e.g., 2σ; see also Schaltegger et al., 2021). (2) Accuracy addresses the difference between a measured value and a reference (or true) value; data might be considered accurate if they lie within reported confidence intervals (Reiners et al., 2017). Furthermore, we suggest that validity – an assessment of how capably and accurately a research tactic measures what it is intended to measure (see definitions for medical, https://www.nlm.nih.gov/oet/ed/stats/02-500.html, last access: 9 October 2025, and social, https://dictionary.apa.org/validity, last access: 9 October 2025, sciences) – is a useful consideration in discussing approaches or algorithms employed to derive geologic information (e.g., MDAs, stratal age) from geochronologic data.

2.3 Results

2.3.1 Slope Mountain DZ U–Pb geochronology

LA-ICPMS results reveal very low proportions of youthful DZ in the samples (Fig. 3), and a general dearth of post-350 Ma zircon is consistent with a transverse provenance signal (Wartes, 2008; Lease et al., 2022). Nearly all (∼99 %) LA-ICPMS dates are pre-Cretaceous (n=762 of 769; Fig. 3; Herriott et al., 2024); only six ${}^{\mathrm{206}}\mathrm{Pb}{/}^{\mathrm{238}}\mathrm{U}$ LA-ICPMS dates (from four of the five DZ samples) are mid-Cretaceous (Table 1) and were potentially sourced from Okhotsk–Chukotka volcanism (Shimer et al., 2016; Akinin et al., 2020; Lease et al., 2022). Two ∼99 Ma LA-ICPMS dates, one each from the lowermost and uppermost samples, are from zircon that did not yield CA-ID-TIMS results (Fig. 3; Table 1); the remaining CA-ID-TIMS experiments ran successfully and yielded concordant dates (Fig. 4). Three of the four DZ grains dated by CA-ID-TIMS were analyzed as “a” and “b” fragments (i.e., multiple analyses) from the same crystal, and each a–b pair yielded dates that overlap at analytical uncertainty and have weighted-mean probabilities of fit >0.05 (Fig. 5; Table 1). The three lowermost samples with Cretaceous DZ have late Albian single-grain CA-ID-TIMS results (101.58 ± 0.13–100.88 ± 0.08 Ma) that get younger up-section (Figs. 5 and 6; Table 1). Sample 18TMH112A from the top of the Slope Mountain stratigraphy yielded a multiple-fragment CA-ID-TIMS result of 102.41±0.03 Ma that is older than the underlying results (Figs. 2, 5, and 6; Table 1). The mid-Cretaceous LA-ICPMS dates mostly overlap at analytical uncertainty, although the dates generally get older up-section (Fig. 5). All of the tandem data have younger LA-ICPMS dates, ranging from one pair yielding nearly the same date (18TMH112A: −0.3 % offset) to one pair not overlapping at ±2σ (Y) uncertainty (18DL001-0.8D: −6.4 % offset; Fig. 5; Table 1).

Figure 3 Normalized kernel density estimations (KDEs) of all detrital zircon (DZ) laser ablation–inductively coupled plasma mass spectrometry (LA-ICPMS) dates from the Slope Mountain samples. All Cretaceous LA-ICPMS dates (±2σ at X) are listed, including their laser ablation analysis labels and tandem-dated z-grain designations. Dates with a single asterisk did not yield chemical abrasion–isotope dilution–thermal ionization mass spectrometry (CA-ID-TIMS) results; the LA-ICPMS date with a double asterisk was not selected for CA-ID-TIMS analysis because the Early Cretaceous result was not poised to yield chronostratigraphically significant constraints. KDEs were plotted in IsoplotR (Vermeesch, 2018), setting kernel bandwidth to calculated (default/auto) values (Botev et al., 2010) and permitting independent (per sample) and adaptive modulation (Abramson, 1982). Rug plots are presented as vertical dashes that mark DZ dates along the time axes; histogram bins are 100 Myr. DZ with ∼800 Ma results are uncommon, and 800 Ma was thus used as the transition between ${}^{\mathrm{206}}\mathrm{Pb}{/}^{\mathrm{238}}\mathrm{U}$ (<800 Ma) and ${}^{\mathrm{207}}\mathrm{Pb}{/}^{\mathrm{206}}\mathrm{Pb}$ (>800 Ma) dates. No discordance filters were employed.

Table 1 Summary of Slope Mountain detrital zircon geochronology samples. All mid-Cretaceous laser ablation–inductively coupled plasma mass spectrometry dates are included, as well as tandem chemical abrasion–isotope dilution–thermal ionization mass spectrometry dates and maximum depositional ages. See Herriott et al. (2024) for complete data tables.

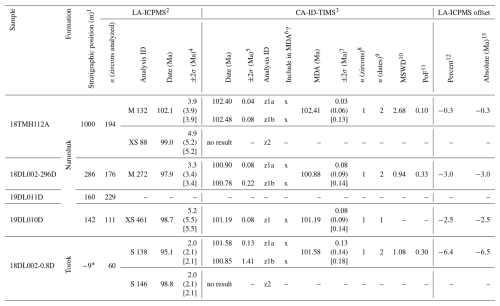
¹ Reference is the base Nanushuk Formation (LePain et al., 2022; Herriott et al., 2024).
² Laser ablation–inductively coupled plasma mass spectrometry; dates are ${}^{\mathrm{206}}\mathrm{Pb}{/}^{\mathrm{238}}\mathrm{U}$.
³ Chemical abrasion–isotope dilution–thermal ionization mass spectrometry; dates are ${}^{\mathrm{206}}\mathrm{Pb}{/}^{\mathrm{238}}\mathrm{U}$.
⁴ Reported as ±2σ analytical uncertainty (analytical uncertainty with standard calibration uncertainty) [analytical uncertainty with standard calibration uncertainty and decay constant uncertainty].
⁵ Reported as ±2σ analytical uncertainty.
⁶ Maximum depositional age; x designates included.
⁷ Reported as ±2σ analytical uncertainty (analytical uncertainty with tracer calibration uncertainty) [analytical uncertainty with tracer calibration uncertainty and decay constant uncertainty].
⁸ Number of zircon grains dated by CA-ID-TIMS.
⁹ Number of zircon dates (whole grains or fragments) obtained by CA-ID-TIMS and included in MDA (all CA-ID-TIMS dates per sample overlap at analytical uncertainty and in all cases are included in the MDA; see text).
¹⁰ Mean square weighted deviation.
¹¹ Probability of fit.
¹² $\text{Percent offset}=\mathrm{100}\cdot (\text{LA-ICPMS date}-\text{CA-ID-TIMS date})/\text{CA-ID-TIMS date}$; where n=2 CA-ID-TIMS dates, the individual analyses are from the same crystal, the dates overlap at analytical uncertainty, PoF>0.05, and the weighted mean (i.e., MDA) is the benchmark.
¹³ $\text{Absolute offset}=\text{LA-ICPMS date}-\text{CA-ID-TIMS date}$; where n=2 CA-ID-TIMS dates, the individual analyses are from the same crystal, the dates overlap at analytical uncertainty, PoF>0.05, and the weighted mean (i.e., MDA) is the benchmark.
^*Plotted at −9 m in Fig. 8.
– Designates no data or not applicable.

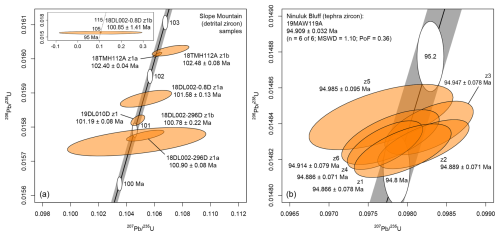
Figure 4 Conventional U–Pb concordia plots (Wetherill, 1956) of all chemical abrasion–isotope dilution–thermal ionization mass spectrometry data for the detrital zircon results at Slope Mountain (a) and tephra zircon results at Ninuluk Bluff (b). Orange uncertainty ellipses reflect 95 % confidence intervals. Inset at upper left includes the relatively imprecise analysis from the 18DL002-0.8D z1b fragment, which is excluded from the main plot on the left. Date uncertainties are ±2σ (X). Plots were generated in IsoplotR (Vermeesch, 2018); gray concordia bands depict the 95 % confidence interval associated with uranium decay constants and ${}^{\mathrm{238}}\mathrm{U}{/}^{\mathrm{235}}\mathrm{U}$ ratio. See Herriott et al. (2024) for complete data tables.

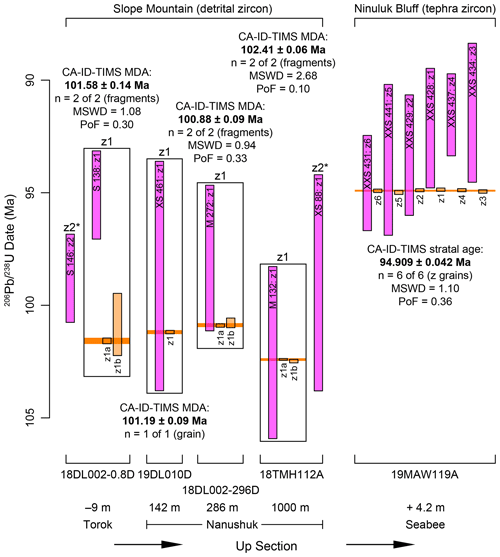
Figure 5 Ranked date plot of tandem-dated detrital zircon (DZ) at Slope Mountain and tephra zircon at Ninuluk Bluff, with laser ablation–inductively coupled plasma mass spectrometry (LA-ICPMS) dates in magenta and chemical abrasion–isotope dilution–thermal ionization mass spectrometry (CA-ID-TIMS) dates in orange. Tandem DZ data are boxed together, including multiple CA-ID-TIMS analyses of fragments from the same crystal. Tandem tephra zircon dates are presented as pairs from left to right, and the stratal age is a weighted mean of all tandem (z-grain) CA-ID-TIMS dates (see also Table 2 and Fig. 7). Interpreted maximum depositional ages (MDAs) (Slope Mountain samples) and stratal age (Ninuluk Bluff sample) are labeled in bold and marked with orange bars that extend across all dates for the included zircon grain(s) but only reflect CA-ID-TIMS data; these interpreted ages are weighted means except for 19DL010D, which has a single-crystal, single-fragment result. Individual dates are plotted at ±2σ (X), and the orange bars and bold ages reflect ±2σ (Y). Labeled z2* grains were selected for analysis by CA-ID-TIMS but did not yield results. Stratigraphic position labels for Torok Formation and Seabee Formation samples are relative to the bottom and top of the Nanushuk Formation, respectively.

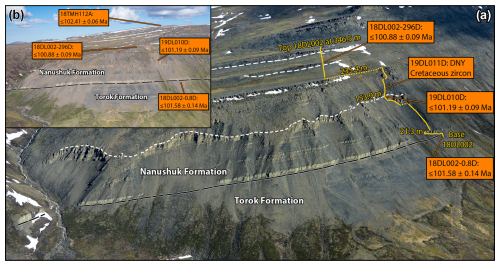
Figure 6 (a) Oblique aerial photograph with view north-northwestward of the southeast flank of Slope Mountain, where the uppermost Torok Formation and the lower part of the Nanushuk Formation crop out. Sample locations and maximum depositional ages (MDAs) based on chemical abrasion–isotope dilution–thermal ionization mass spectrometry are labeled and placed in the context of the measured section by LePain et al. (2022; yellow labels and lines denote measured section meters and route of that study; see Fig. 1 for location). Figure adapted from LePain et al. (2022; see therein for discussion of intra-Nanushuk surfaces (dashed white lines)); the short-dash, queried line at 153.9 m is the incised-valley surface of LePain et al. (2009; also Schenk and Bird, 1993). (b) Oblique aerial photograph with view northwestward of the southeast flank and higher topography of Slope Mountain, including the site of the uppermost detrital zircon sample (18TMH112A; note that this MDA is not chronostratigraphically significant). Uncertainties are reported at ±2σ (Y). DNY – did not yield.

2.3.2 Ninuluk Bluff tephra zircon U–Pb geochronology

Eleven of the 14 zircons analyzed by LA-ICPMS from 19MAW119A yielded Late Cretaceous dates, ranging from ∼89.6 to ∼94.6 Ma (Figs. 5 and 7; Table 2; Herriott et al., 2024). Weighted means for all 11 Cretaceous LA-ICPMS dates (92.75±0.84 (1.45) Ma) and all 6 tandem-dated crystal dates (92.72±1.02 (1.56) Ma) from this sample are nearly identical (Fig. 7). The six crystals plucked for tandem analyses yield a CA-ID-TIMS-based weighted mean of 94.909±0.032 (0.042) Ma (Figs. 5 and 7; Table 2). All three weighted means of Fig. 7 exhibit date distributions and uncertainties that are consistent with expected degrees of analytical dispersion for a single population sample (Wendt and Carl, 1991; Spencer et al., 2016). All of the tandem data have younger LA-ICPMS dates, ranging from one pair yielding nearly the same date (z6: −0.36 % offset) to two pairs not overlapping at ±2σ (X or Y) uncertainty (z4: −3.52 % offset; z3: −3.68 % offset; Fig. 5; Table 2).

Figure 7 (a) Ranked date plot of Cretaceous laser ablation–inductively coupled plasma mass spectrometry dates (LA-ICPMS; magenta data) and chemical abrasion–isotope dilution–thermal ionization mass spectrometry dates (CA-ID-TIMS; orange data) from the Ninuluk Bluff tephra zircon sample (19MAW119A). The LA-ICPMS weighted-mean date for all the Cretaceous LA-ICPMS results is graphically presented (2σ at Y) as the magenta bar that extends across the plot, and the LA-ICPMS weighted-mean date for the tandem-dated grains is also listed. Neither of the LA-ICPMS weighted means overlaps at 2σ (Y) with the CA-ID-TIMS weighted mean (see narrow orange bar that extends across the plot), which we interpret as the stratal age for this sample. Both LA-ICPMS weighted means have ∼2.3 % young bias (see text and Fig. 10). Individual dates are plotted at ±2σ (X), and colored weighted-mean date bars reflect uncertainty at Y (see confidence intervals listed in bold). (b) Probability density plots (DensityPlotter; Vermeesch, 2012) of the three pooled sets of dates from (a). Each white and black box along the x axis marks 0.2 Myr, which could reflect several tens of meters of stratigraphic accumulation in, for example, the Nanushuk Formation and perhaps a single magmatic zircon crystallization cycle (see text for details). We highlight this in the context of considerations of geologic rates and durations of interest and the appropriate relative geochronologic precision and accuracy required to adequately address research questions posed in case studies. Rug plots (IsoplotR; Vermeesch, 2018) per pooled/plotted date set are presented as vertical lines that mark dates along the time axis.

Table 2 Summary of Ninuluk Bluff air-fall tephra zircon geochronology sample 19MAW119A (Seabee Formation). All laser ablation–inductively coupled plasma mass spectrometry dates are included, as well as tandem chemical abrasion–isotope dilution–thermal ionization mass spectrometry dates and weighted-mean stratal age. See Herriott et al. (2024) for complete data tables.

¹ Above top Nanushuk Formation (see Herriott et al., 2024).
² Laser ablation–inductively coupled plasma mass spectrometry; dates are ${}^{\mathrm{206}}\mathrm{Pb}{/}^{\mathrm{238}}\mathrm{U}$.
³ Chemical abrasion–isotope dilution–thermal ionization mass spectrometry; dates are ${}^{\mathrm{206}}\mathrm{Pb}{/}^{\mathrm{238}}\mathrm{U}$.
⁴ Reported as ±2σ analytical uncertainty (analytical uncertainty with standard calibration uncertainty) [analytical uncertainty with standard calibration uncertainty and decay constant uncertainty].
⁵ Reported as ±2σ analytical uncertainty.
⁶ Weighted mean (i.e., interpreted stratal age); x designates included.
⁷ Reported as ±2σ analytical uncertainty (analytical uncertainty with tracer calibration uncertainty) [analytical uncertainty with tracer calibration uncertainty and decay constant uncertainty].
⁸ Number of zircon grains analyzed by CA-ID-TIMS (all are single analyses per grain; all analyses ran successfully and yielded concordant dates).
⁹ Number of zircon grain dates obtained by CA-ID-TIMS that overlap at analytical uncertainty.
¹⁰ Number of zircon dates included in the weighted-mean stratal age.
¹¹ Mean square weighted deviation.
¹² Probability of fit.
¹³ $\text{Percent offset}=\mathrm{100}\cdot (\text{LA-ICPMS date}-\text{CA-ID-TIMS date})/\text{CA-ID-TIMS date}$; the CA-ID-TIMS date is from the same crystal as the LA-ICPMS date (i.e., the benchmark is the tandem CA-ID-TIMS individual crystal date and
not the CA-ID-TIMS weighted-mean stratal age).
¹⁴ $\text{Absolute offset}=\text{LA-ICPMS date}-\text{CA-ID-TIMS date}$; the CA-ID-TIMS date is from the same crystal as the LA-ICPMS date (i.e., the benchmark is the tandem CA-ID-TIMS individual crystal date and not the CA-ID-TIMS
weighted-mean stratal age).
^*Plotted at 1004.2 m in Fig. 8; correlation to Slope Mountain is regarded as providing a minimum age constraint at that height, as discussed in the text.
– Designates no data or not applicable.

2.4 Analysis: Slope Mountain and Ninuluk Bluff

2.4.1 Slope Mountain DZ MDAs

We interpret each single-crystal, CA-ID-TIMS result from the Slope Mountain DZ samples as an MDA (Figs. 5 and 6; Table 1). These late Albian MDAs are notably younger than previous age constraints (see below). The lack of LA-ICPMS ${}^{\mathrm{206}}\mathrm{Pb}{/}^{\mathrm{238}}\mathrm{U}$ Cretaceous dates from 19DL011D, as well as an older MDA for 18TMH112A, reflects common challenges in DZ studies, where chronostratigraphically significant youthful zircons are geologically absent or were not successfully sampled and analyzed. Sample 18TMH112A from the top of the Slope Mountain stratigraphy did yield an analytically excellent MDA that is nevertheless ∼1 Myr older than the otherwise oldest MDA from sample 18DL002-0.8D at the base of the studied section (e.g., Fig. 6). The multiple-fragment-based CA-ID-TIMS dates from 18DL001-0.8D, 18DL002-296D, and 18TMH112A bolster confidence that the single-grain MDAs are accurate by demonstrating intra-grain experimental reproducibility (e.g., Fig. 5) and diminishing the possibility that intransigent Pb loss, which is unlikely to be uniform among grain fragments from the same crystal, is impacting results. There is, however, nontrivial risk of losing or destroying a zircon during physical fragmentation, and using an entire grain for a single CA-ID-TIMS analysis may yield an analytically better result for very small zircon with limited radiogenic Pb. Sample 19DL010D is an example of the non-fragmentation approach (Fig. 5; Table 1). Sample 18DL002-296D demonstrates a common a–b fragment precision relation, with a physically larger “a” fragment yielding a higher-precision date than the physically smaller “b” fragment. Sample 18TMH112A also exhibits this general a–b fragment precision relation, but also note that the “a” fragment yielded the most precise CA-ID-TIMS date reported herein (±0.04 % at X) and the “b” fragment is also a very high-precision result (±0.08 % at X; Fig. 4; Table 1). The most marked example of lower-precision b-fragment data is from 18DL002-0.8D (Fig. 4; Table 1), which yielded a chronostratigraphically significant MDA that is younger than existing biostratigraphic constraints, is from the lowest/oldest sample in the section, and lies immediately below the Torok–Nanushuk transition (Figs. 5 and 6). Obtaining a higher-precision b-fragment CA-ID-TIMS date from 18DL002-0.8D would have been preferable, but the benefits of demonstrating reproducibility via the multiple-analysis approach are evident in this sample.

2.4.2 Ninuluk Bluff tephra zircon age

We interpret the 94.909±0.032 Ma weighted-mean date (n=6 of 6) as the depositional age for the tephra sample (19MAW119A) at Ninuluk Bluff (Figs. 5 and 7; Table 2). The average analytical uncertainty for the individual CA-ID-TIMS analyses from this sample is ±0.079 Ma (±0.083 %), which coincides with common apparent crystallization durations (e.g., ≤10⁵ years) for autocrystic zircon populations (e.g., Crowley et al., 2007; Wotzlaw et al., 2013, 2014; Keller et al., 2018; Pamukçu et al., 2022). The geologic, geochronologic, and statistical context of these CA-ID-TIMS dates and pooled-age goodness-of-fit metrics suggest that the results are consistent with a single geologic population and that the data may resolve a magmatic zircon crystallization event. In contrast, the LA-ICPMS tandem dates for this sample have average analytical uncertainties of ±2.67 Ma (±2.88 %). Even if the paired LA-ICPMS data were highly accurate, these analytical uncertainty envelopes could encompass many magmatic cycles (references above) and hundreds of meters of stratigraphy – perhaps entire formations – at typical active margin sedimentation rates (e.g., 10² m Myr⁻¹; Miall et al., 2021; Fig. 7b). Analytical uncertainty sets the threshold for the potential to discriminate geologic populations and processes (Schaltegger et al., 2015), and thus LA-ICPMS currently lacks the analytical resolution to truly establish geological (e.g., xenocrystic–antecrystic–autocrystic scatter) versus analytical dispersion for mid-Cretaceous zircon (see Fig. 7b).

The analytical resolution limitations of LA-ICPMS are clear, yet it is the paired LA-ICPMS result for each tandem-dated tephra zircon from 19MAW119A that is most conspicuous: each LA-ICPMS date has a young bias (i.e., negative offset; Table 2; also Figs. 5 and 7). The offset for the n=11 LA-ICPMS weighted mean is −2.27 %, which is nearly identical to the offset of −2.31 % for the n=6 LA-ICPMS weighted mean that solely includes the tandem dates (Fig. 7). The goodness-of-fit metrics for each of the weighted means in Fig. 7 only establish that excess scatter is not evident in the data at the level of analytical resolution of the individual dates and cannot preclude systematic bias (Schaltegger et al., 2015). In fact, neither weighted mean from the LA-ICPMS dates overlaps at ±2σ (Y) with the CA-ID-TIMS-based stratal age (Fig. 7), highlighting that both statistical assessments of dispersion and the accuracy of underlying dates should be considered in a comprehensive interpretive framework.

2.4.3 Slope Mountain chronostratigraphy

The uppermost Torok Formation MDA indicates that the Nanushuk Formation at Slope Mountain is $\le \mathrm{101.58}\pm \mathrm{0.13}$ (0.14) [0.18] Ma, which is ∼8.5 Myr younger than previous biostratigraphic information suggested (Fig. 8). Regional stratigraphic relations (e.g., Keller et al., 1961; Detterman et al., 1963; Huffman et al., 1981; LePain et al., 2009) also permit integration of the tephra age from Ninuluk Bluff with the Slope Mountain stratigraphy. The marine–non-marine–marine Nanushuk Formation stacking relations at Slope Mountain (e.g., Fig. 2) and the recessive outcrop character of bentonitic Seabee Formation mudstone and shale (Mull et al., 2003; Herriott et al., 2018) broadly support the stratigraphic correlation between upper Nanushuk at Slope Mountain, where Seabee is absent, and upper Nanushuk at Ninuluk Bluff, where the Nanushuk–Seabee transition crops out (LePain et al., 2009; LePain and Kirkham, 2024; Fig. 2). Existing Nanushuk–Torok clinothem DZ MDAs reveal potentially synchronous drowning of Ninuluk sandstone-associated depositional systems during the final stage of Nanushuk deposition (Lease et al., 2022). Conceptually, however, Ninuluk Bluff is in a more landward position relative to the Nanushuk–Torok ultimate shelf margin than Slope Mountain is (Fig. 1a; Houseknecht, 2019b), suggesting that any diachroneity in the lithostratigraphic units would perhaps be reflected by the onset of (topset) Seabee sedimentation at Slope Mountain prior to the onset of (topset) Seabee sedimentation at Ninuluk Bluff (Fig. 2). Furthermore, it is not known how much upper Nanushuk stratigraphy (i.e., Ninuluk sandstone) has been eroded from the summit of Slope Mountain. Collectively, these time and stratigraphy considerations support the supposition that the 18TMH112A sample horizon at the Slope Mountain summit is not younger than 94.909±0.032 Ma.

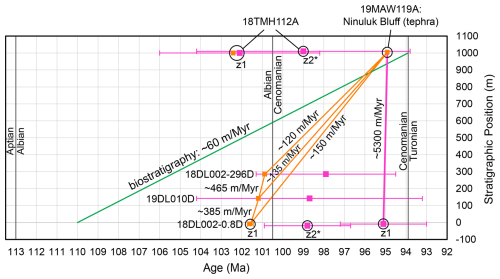
Figure 8 Age–depth plot of new and existing age constraints for the Slope Mountain stratigraphy. Data plotted in magenta and orange are laser ablation–inductively coupled plasma mass spectrometry (LA-ICPMS) and chemical abrasion–isotope dilution–thermal ionization mass spectrometry (CA-ID-TIMS) constraints, respectively; generalized biostratigraphic constraints are plotted in green. Note that z2 from 18DL002-0.8D and z2 from 18TMH112A did not yield CA-ID-TIMS results (labeled with asterisks); although a solely LA-ICPMS-based study may have considered these dates in a chronostratigraphic analysis, neither of these z2 detrital zircon grains (plotted with slight height offsets for clarity) is poised to change any conclusions herein. Uncertainty bars for LA-ICPMS and CA-ID-TIMS results are ±2σ (Y) and are generally obscured by point symbols for the latter. Each stratigraphic accumulation rate between an MDA and the tephra age is a minimum; line-segment rates between MDAs are neither minimums nor maximums.

We thus interpret the Slope Mountain Nanushuk Formation to be $\le \mathrm{101.58}\pm \mathrm{0.13}$ (0.14) [0.18] Ma and $\ge \mathrm{94.909}\pm \mathrm{0.032}$ (0.042) [0.110] Ma. One implication of these markedly narrowed age constraints is that the erosion surface at 153.9 m of Fig. 6 (∼144 m above Torok; see LePain et al., 2009, 2022) may not reflect significant geologic time. The new MDAs also indicate that this cut-and-fill succession may be temporally associated with widespread paleoenvironmental changes and hiatuses and shelfal incisions noted elsewhere during the Albian–Cenomanian transition (e.g., Koch and Brenner, 2009; Schröder-Adams, 2014; Lease et al., 2024).

A simple age–depth assessment of the Nanushuk Formation at Slope Mountain demonstrates the value and challenges of single-grain LA-ICPMS DZ dates and CA-ID-TIMS MDAs of this study. Using the 94.909±0.032 Ma age from Ninuluk Bluff as a minimum age constraint for the top of Nanushuk at Slope Mountain, each straight-segment, accumulation-rate pathway between a CA-ID-TIMS DZ MDA and the (overlying) tephra age in Fig. 8 represents a minimum value; the chronostratigraphically insignificant MDA from 18TMH112A is excluded from the analysis. These minimum accumulation rates, which are derived from shallow-marine and non-marine topset strata, are consistent with 10⁶-year duration sedimentation in a tectonically active foreland basin (e.g., Miall et al., 2021), with an overall minimum rate for the entire section of $\sim \mathrm{150}\mathrm{m}{\mathrm{Myr}}^{-\mathrm{1}}$ (Fig. 8). Segments separately tying the two overlying MDAs to the tephra age reveal slightly lower (minimum) rates than the overall $\sim \mathrm{150}\mathrm{m}{\mathrm{Myr}}^{-\mathrm{1}}$ (minimum) rate for the entire section because the three lowermost MDAs are steeply stacked in age–depth space (Fig. 8). A minimum stratigraphic accumulation-rate context does not apply to line segments between the CA-ID-TIMS MDAs in the lower ∼300 m of sampled stratigraphy at Slope Mountain, as crystallization-to-sedimentation lag times can (geologically) vary between samples. Additionally, field, laboratory, and analytical sampling factors (see Dröllner et al., 2021; Lowey, 2024) further impact the inter-sample variability of lag time relations, such that any between-MDA rate cannot be characterized as a minimum or maximum.

Interpreting the Slope Mountain LA-ICPMS single-grain dates as MDAs (i.e., YSGs) would render an inaccurate (at 2σ at Y) chronostratigraphic framework. The lowermost sample in the section yielded the youngest and most precise LA-ICPMS date (95.1±2.0 (2.1) Ma) from Slope Mountain and exhibits the greatest tandem-date pair offset (−6.4 % and −6.5 Myr; Table 1). The overlying samples yielded older LA-ICPMS dates, although all of the youngest single LA-ICPMS dates from the four Slope Mountain samples with mid-Cretaceous results overlap at analytical uncertainty (Figs. 5 and 8). A stratigraphic accumulation rate derived from the youngest 18DL002-0.8D LA-ICPMS DZ date and the new tephra zircon age is implausibly rapid ($\sim \mathrm{5300}\mathrm{m}{\mathrm{Myr}}^{-\mathrm{1}}$ for the entire section; Fig. 8); however, permitting the rate (line segment) to wander the full extent of this LA-ICPMS date's +2σ (Y) value could reduce the rate to $\sim \mathrm{440}\mathrm{m}{\mathrm{Myr}}^{-\mathrm{1}}$, which is plausible yet notably less probable. Nearly any rate derived from the youngest 18DL002-0.8D LA-ICPMS DZ date minus some component of 2σ is nonsensical from a sediment accumulation perspective, where either the age–depth pathway would indicate instantaneous sedimentation for the entire bracketed section or the age and stratigraphic relations would contravene superposition. The exercise of simplistically wandering the ±2.2 % (Y) uncertainty envelope for this single-grain result also demonstrates that LA-ICPMS is sometimes not well suited to deriving stratigraphic accumulation rates. Although age constraints from throughout a section can improve the probabilistic context of LA-ICPMS results in deep-time applications (e.g., Johnstone et al., 2019; Coutts et al., 2024), the underlying data should be accurate for such an analysis to be valid.

The new U–Pb data presented here are an example of how useful MDAs are when (1) tandem CA-ID-TIMS analyses are employed to obtain accurate and appropriately precise results to resolve chronostratigraphic relations of interest, (2) the youngest analyzed DZs are near stratal age, and (3) accurate and appropriately precise independent stratal age constraints are available (Fig. 8). Absent the tandem CA-ID-TIMS data, however, we would have been faced with the decision of how to treat the LA-ICPMS results from Slope Mountain, with the end-member choices being (a) discount the results or (b) note how remarkably young the strata are and how rapid the stratigraphic accumulation rates were.

3 Discussion: evaluating DZ MDAs in light of tandem-date relations

3.1 Challenges of LA-ICPMS-based MDAs

In the following sections we consider potential impacts of several sources of uncertainty in DZ MDA chronostratigraphic research and provide a tandem-date-based framework for evaluating these challenges. The emphasis is on DZ MDA geochronology of Meso-Cenozoic strata, partly reflecting a common focus on post-Paleozoic basins and the typical temporal resolution of the mass spectrometry methods employed relative to the geologic processes (e.g., magmatism, stratigraphic accumulation rates) and common durations (e.g., 10⁵–10⁶ years) of interest.

3.1.1 Analytical dispersion and MDA validation

Random errors are ubiquitous in measurements, including geochronology, with measured values bearing a random component of deviation relative to true values (e.g., Reiners et al., 2017). In cases where the only source of uncertainty is random and the number of measurements is appropriately high, the mean of the measurements should approximately coincide with the true value being measured, and the data dispersion can be quantified and reported at a given confidence interval (e.g., Schoene et al., 2013). Random errors in geochronology are commonly observed, presumed, and modeled to have normal (Gaussian) distributions, where ∼68 % and ∼95 % of the underlying data lie within ±1σ and ±2σ of the mean, respectively (e.g., McLean et al., 2011; Schoene et al., 2013; Reiners et al., 2017; Vermeesch, 2021). LA-ICPMS measurements of U and Pb isotope ratios include random statistical fluctuations during analysis that are reflected in the dispersion of data used to derive the standard error of the mean (i.e., σ as typically noted in geochronologic literature (e.g., Horstwood et al., 2016), with $\mathrm{2}\cdot \mathit{\sigma }=\mathrm{2}\mathit{\sigma }$) for each spot date (e.g., Sundell et al., 2021). It is important to note these uncertainties for LA-ICPMS dates are effectively a measure of analytical precision and lack explicit bearing on accuracy due to systematic uncertainties that must also be considered and are not fully characterized (e.g., Schoene, 2014; Schaltegger et al., 2015; Horstwood et al., 2016; Herriott et al., 2019a; this study). Nevertheless, the typical net effect of the normal distribution of individual date uncertainties is that many geochronologic dates obtained from a single geologic population are themselves typically normally distributed relative to a mean (ideally true) value (e.g., Coutts et al., 2019). These data dispersion relations are not unique to LA-ICPMS U–Pb geochronology, but the typical magnitude of analytical uncertainty; common population sampling densities of DZ; and dates, rates, and durations of interest for Meso-Cenozoic strata suggest that random scatter should be carefully evaluated for potential to impart chronostratigraphically significant error to LA-ICPMS-based MDAs.

In advocating for single-grain-based MDAs, Copeland (2020) considered possible impacts of analytical dispersion and concluded that preferentially sampling the young low-probability tail of a distribution of detrital dates would “rarely” be problematic because of the minimal area (∼2.5 %) under a Gaussian probability curve that lies beyond a mean-minus-2σ value. An ${}^{\mathrm{40}}\mathrm{Ar}{/}^{\mathrm{39}}\mathrm{Ar}$ dataset (McIntosh and Ferguson, 1998) example was provided, with a youngest date reportedly overlapping at ±2σ with a weighted mean from two rhyodacite samples (Copeland, 2020). It is unclear how the youngest ${}^{\mathrm{40}}\mathrm{Ar}{/}^{\mathrm{39}}\mathrm{Ar}$ date (18.33±0.15 Ma at 2σ; McIntosh and Ferguson, 1998) overlaps the weighted-mean date (reported by Copeland, 2020, as 18.59±0.02 Ma), which is also characterized by overdispersion (probability of fit=0.00). Regardless of the details for the high-precision volcanic sample data, we appreciate that at low- to moderate-n sampling, the youngest date from a single geologic population will probably be greater than the mean-minus-2σ value. However, the probability that the youngest date will be less than a population-mean-minus-2σ value increases with higher-n sampling (e.g., Vermeesch, 2021). Analytical scatter is random, but methodically sampling the low-probability tail of a date distribution via, for example, the YSG algorithm can systematically render impactful young bias in MDAs and chronostratigraphic interpretations derived from LA-ICPMS data at ±2 %–4 % analytical precision.

Analytical dispersion provides a straightforward opportunity to reconsider long-standing characterizations of YSG, which is typically described as likely to closely coincide with stratal age while also being prone to yielding MDAs younger than stratal age (e.g., Dickinson and Gehrels, 2009; Coutts et al., 2019; Sharman and Malkowski, 2020), and how we assess the reliability or success or accuracy of the MDA algorithms. A proponent of YSG in general – and within the context of analytical dispersion specifically – might rely on the numerical modeling of Coutts et al. (2019). Those authors concluded that YSG and other low-n (i.e., 1–3) metrics were generally “the most successful and accurate” MDA algorithms. However, they also noted that low-n algorithm DZ MDAs are susceptible to being younger than depositional age, especially when youthful DZs are abundant and overall n and analytical uncertainty are high. Coutts et al. (2019) used LA-ICPMS-scale analytical dispersion as the sole source of uncertainty in the modeled DZ dates, and the performance of YSG and other MDAs in that study were evaluated by comparing modeled DZ dates to a “synthetic” true depositional age (TDA). The modeled dates were themselves extracted from age populations that ranged from 93 to 80 Ma, with the latter being the synthetic TDA. The range of near-depositional-age DZ dates and the fact that MDA residual offset metrics in the numerical modeling were established by evaluating MDAs relative to TDAs likely elevated apparent successes of YSG and other low-n algorithms.

Characterizing the differences between MDAs and TDAs is valuable (see Sharman and Malkowski, 2020), but these differences are an assessment of zircon crystallization-to-sedimentation lag times, which do not directly bear on the accuracy of MDAs. Coutts et al. (2019) noted that “little has been done to quantitatively assess the ability of the different [MDA] calculation methods to reliably reproduce the true depositional age (TDA) of a rock, referred to herein as the accuracy [their emphasis] of the calculated MDA”. However, accuracy in geochronology (and metrology in general) is an assessment of the coincidence of a measured value with the reference or true value (e.g., Condon and Schmitz, 2013; Schoene et al., 2013; Reiners et al., 2017; Schaltegger et al., 2021). The accuracy benchmark for an MDA is not the sampled bed's TDA. The valid benchmark for DZ MDA accuracy is the true age or reference value of the youngest analyzed zircon population in the sample. The intent of the approach by Coutts et al. (2019) is understandable, but it is the chronostratigraphic significance of an (accurate) MDA that increases as it approaches the TDA (i.e., as crystallization-to-sedimentation lag time →0). Comparing MDAs with existing chronostratigraphic data does not ascertain – and cannot quantify – MDA accuracy because MDAs are one-sided, maximum constraints that have no radioisotopic tie to stratal age. The singularly critical relationship between (accurate) MDAs and (accurate) TDAs is based on the principle of inclusions, such that TDA ≤ MDA. MDAs may be discounted where chronostratigraphic relations definitively preclude their accuracy, although such scenarios are uncommon in case studies. DZ MDA versus volcanic strata age tests or comparisons are sometimes carried out (e.g., Daniels et al., 2018; Lease et al., 2022), but situations where microbeam-based MDAs are younger than existing age constraints commonly render chronostratigraphic dilemmas that may be intractable without tandem data (e.g., Herriott et al., 2019a, b).

So, MDAs that appear to be an excellent proxy for stratal age can be inaccurate, a situation we colloquially refer to as seemingly getting the right answer but for the wrong reason(s). An MDA algorithm that has a propensity to yield what may seem like a correct and chronostratigraphically significant result (e.g., MDA coincides with TDA) by providing the solution to a question that cannot be directly answered with DZ (i.e., what is the stratal age?) should not be characterized as a reliable approach based on that line of reasoning. And an MDAs-as-TDAs framing itself lacks validity. Integrating existing age data with new DZ MDAs is valuable and should continue as chronostratigraphic records are refined, but the practice of using existing age controls to benchmark the accuracy of MDAs can be abandoned.

U–Pb data from Ninuluk Bluff provide another opportunity to examine analytical dispersion as a source of negative offsets for single-grain MDAs and the limitations of chronostratigraphic benchmarking for evaluating MDA metrics. LA-ICPMS DZ dates from Ninuluk Bluff (Lease et al., 2022) can be compared to the CA-ID-TIMS-based air-fall tephra age reported here. The DZ sample was collected from the uppermost 18 m of Nanushuk (∼4 to ∼22 m below 19MAW119A) and yielded a youngest grain cluster algorithm (YGC 2σ sensu Coutts et al., 2019) MDA of 95.1±0.5 [1.3] Ma. A YSG of 93.0±2.3 Ma (2σ at X) derivation from this sample overlaps the 94.909±0.032 (0.042) Ma minimum age constraint for the top of Nanushuk at Ninuluk Bluff (Table 2), as well as the preferred MDA of Lease et al. (2022). However, a stratigrapher relying on that YSG in a chronostratigraphic analysis would understandably interpret the result as indicating that the top of Nanushuk is probabilistically most likely to be no older than early Turonian (cf. Mull et al., 2003). A careful interpreter would also appreciate that this YSG might reflect sedimentation as old as late Cenomanian within a ∼95 % probability context (i.e., $\mathrm{93.0}\mathrm{Ma}+\mathrm{2.3}\mathrm{Ma}=\mathrm{95.3}\mathrm{Ma}$), but it is just as probable that that YSG is indicating a late Turonian MDA (i.e., $\mathrm{93.0}\mathrm{Ma}-\mathrm{2.3}\mathrm{Ma}=\mathrm{90.7}\mathrm{Ma}$) in the holistic context of ±2σ. Yet, the new tephra age precludes Nanushuk at Ninuluk Bluff from being younger than 94.909 ± 0.032 (0.042) Ma (Figs. 7 and 8). And the probability of fit (0.31) for the YGC 2σ MDA of Lease et al. (2022) suggests that their multi-grain selection exhibits dispersion consistent with analytical scatter; in other words, the YSG we derived from their Ninuluk Bluff DZ sample is selectively sampling the low-probability tail of a distribution of dates from what may be a single population as resolved by LA-ICPMS.

The poor performance of YSG at Ninuluk Bluff highlights how CA-ID-TIMS constraints can break through theoretical discussions of the merits and limitations for single-grain LA-ICPMS-based MDAs by empirically demonstrating impactful young bias for YSG at moderate-n and moderate-precision sampling of youthful DZ where the date distribution is consistent with the nature of measurement dispersion for a single population. However, the CA-ID-TIMS air-fall tephra age of this study can only establish that the multi-grain MDA of Lease et al. (2022) is not younger than stratal age, whereas quantifying whether that YGC 2σ MDA is an accurate measure of the youngest zircon population sampled requires CA-ID-TIMS of the same DZ crystals that were analyzed by LA-ICPMS. The typical chronostratigraphic-pattern-matching measures of success for single- and multi-grain MDAs are not measures of accuracy (see above) but, again colloquially speaking, effectively assessments of staying out of trouble (i.e., deriving MDAs that coincide with or are older than TDAs).

Sample 19MAW119A is another empirical example of the strengths and challenges of single-grain versus multi-grain, microbeam-based chronostratigraphic constraints in the context of analytical dispersion. This tephra appears to be relatively simple geologically and geochronologically, yet neither the youngest LA-ICPMS zircon date nor a weighted mean from the in situ analyses overlaps at 2σ (Y) the CA-ID-TIMS age (Fig. 7). The distribution of Cretaceous LA-ICPMS dates is consistent with random scatter during analyses of zircon from a single population (Fig. 7), and the nature of the sample avoids the potentially geologically and statistically fraught pooling of DZ dates from zircon of unknown relatedness (Spencer et al., 2016; Copeland, 2020; cf. Vermeesch, 2021). Nevertheless, there are conspicuous and impactful negative offsets across the microbeam data (Fig. 7). And, finally, each of the youthful DZ population(s) samples obtained by LA-ICPMS for the Slope Mountain sample suite are either n=1 or n=2 (Fig. 3), where the expected distribution of analytical dispersion is effectively undefined, but YSGs derived from those data ubiquitously exhibit negative offsets (Fig. 5). YSG should, on average, perform better where analytical dispersion is the sole source of uncertainty and youthful-population sampling density is very low. YSG performance will increasingly degrade with increasingly high-n sampling of youthful DZ populations (e.g., see Coutts et al., 2019; Gehrels et al., 2020; Vermeesch, 2021; Sharman and Malkowski, 2024; Sundell et al., 2024). However, any DZ MDA algorithm assessment that solely focuses on analytical dispersion of LA-ICPMS dates will be inconclusive, and both the youthful DZ data and the tephra zircon results of this study likely carry sources of negative offset beyond analytical dispersion.

3.1.2 Pb loss

Geochronologists have explored discordance and Pb loss since the first U–Pb dates were published (Tilton et al., 1955; Tilton, 1956; Wetherill, 1956; see also Mattinson, 2005, 2011, 2013). Mitigating detrimental impacts of open-system behavior remains at the forefront of obtaining accurate zircon dates (e.g., Schaltegger et al., 2015, 2021), and U–Pb dates with young bias may reflect Pb loss (e.g., Schoene, 2014). CA-ID-TIMS (Mattinson, 2005) provides state-of-the-art Pb-loss mitigation and accuracy for U–Pb zircon geochronology, including for chronostratigraphic applications (e.g., Mundil et al., 2004; Bowring et al., 2006; Schmitz and Kuiper, 2013; Schoene et al., 2015, 2019; Schmitz et al., 2020; Ramezani et al., 2022). Efforts to adapt chemical abrasion to U–Pb dating of zircon by LA-ICPMS are promising (Crowley et al., 2014; von Quadt et al., 2014; Donaghy et al., 2024; see also Gehrels, 2012), although there are some complicating factors (Schaltegger et al., 2015; Horstwood et al., 2016; see also Ver Hoeve et al., 2018). Donaghy et al. (2024) recently demonstrated marked potential for chemical abrasion–LA-ICPMS to improve DZ geochronology. Apparent Pb-loss modeling by Sharman and Malkowski (2024) and the study by Howard et al. (2025) are also likely to instill additional focus on pre-treatment for in situ U–Pb zircon dating (see also chemical abrasion–SIMS studies by, e.g., Kryza et al., 2012; Watts et al., 2016; Kooymans et al., 2024).

Discordance-based evaluation of Pb loss from zircon younger than ∼400 Ma requires high-precision ratios (e.g., Bowring and Schmitz, 2003; Bowring et al., 2006; Spencer et al., 2016), which LA-ICPMS does not provide. Pb loss via volume diffusion at high temperatures (e.g., >900 °C; Cherniak and Watson, 2001) is seemingly irrelevant to many DZ MDA studies (Vermeesch, 2021). However, Pb loss may also occur as the result of relatively low-temperature, fluid-mediated processes (e.g., see Schoene, 2014) and likely is associated with radiation damage and fractures (e.g., Bowring and Schmitz, 2003). Keller et al. (2019) further suggested that low-temperature recrystallization of zircon in the presence of water during weathering and subaerial erosion can lead to Pb loss, potentially rendering the incompatibility of Pb in zircon as a Pb-loss liability under conditions that are relatively common in sedimentary basins and incipient or modern outcrops (see also Andersen et al., 2019; Andersen and Elburg, 2022). Low-temperature, aqueous-process-related Pb loss and/or recrystallization and/or overgrowth thus may impact chronostratigraphic studies that derive MDAs from DZ, as noted by Sharman and Malkowski (2020, 2024). Ultimately, relatively young sedimentary basins (e.g., Meso-Cenozoic) with zircon residing in below-geologic-annealing temperatures (e.g., <100–250 °C) may be somewhat counterintuitively prone to losing Pb as alpha damage and fission tracks accumulate in a zircon crystal lattice (see Herrmann et al., 2021). Copeland (2020) considered several aspects of Pb loss but concluded the phenomenon is mostly a challenge for petrologists rather than stratigraphers. And Vermeesch (2021) highlighted a so-called forbidden zone in a series of plots of LA-ICPMS- versus CA-ID-TIMS-based MDAs where the former are younger than the latter but suggested that Pb loss in DZ, which could account for such a data relation, is probably uncommon in sedimentary basins because they are not typically subject to elevated temperatures (e.g., >900 °C) that would promote Pb loss by diffusion. The plots Vermeesch (2021) referred to (Fig. 4 therein) are based on LA-ICPMS and CA-ID-TIMS DZ dates from the companion studies of Gehrels et al. (2020) and Rasmussen et al. (2021), with the latter study concluding that most of the analyzed zircon had lost Pb. Similarly, a tandem DZ dataset from Jurassic strata has also been interpreted to reveal Pb loss from zircon (Herriott et al., 2019a). Below we examine these two previously published tandem DZ datasets (Herriott et al., 2019a; Rasmussen et al., 2021), as well as the tandem-date pairs from this study, in a percent-offset context to gain new insights into potential systematic and/or open-system sources of young bias for zircon dates, starting with Pb loss.

Rasmussen et al. (2021) presented LA-ICPMS–CA-ID-TIMS tandem-date pairs for 13 DZ samples from within and below the Upper Triassic Chinle Formation (Arizona, USA; Fig. 2 therein), which was likely deposited in a back-arc basin associated with active magmatism. We assessed date pair (n=110) relations for 10 samples from the Chinle study. Negative offsets are prevalent: 96 of 110 LA-ICPMS dates are younger than their paired CA-ID-TIMS dates, with average overall offsets of −2.2 % and −4.9 Myr (Figs. 9 and 10). For reference, the average 2σ uncertainty (Y; our assessment) for the tandem LA-ICPMS dates is ±2.8 % and ±6.0 Myr. Average offsets for the 10 tandem YSGs (i.e., the youngest LA-ICPMS date per sample that has a paired CA-ID-TIMS date) are −4.1 % and −9.0 Myr, with each tandem YSG being younger than its paired CA-ID-TIMS dates (3 tandem-date pairs overlap at 2σ at Y). In the companion study, Gehrels et al. (2020) presented a larger DZ dataset that included the tandem Chinle Formation data, with a focus on the LA-ICPMS results. Gehrels et al. (2020) used the maximum likelihood age (MLA) algorithm (adapted from thermochronologic mixture modeling; see Vermeesch, 2021) to establish their preferred LA-ICPMS-based MDAs. Rasmussen et al. (2021) established MDAs with a coherent age cluster weighted-mean tactic, with the CA-ID-TIMS-based MDAs typically being older than the LA-ICPMS-based MDAs, although the per-sample-paired MDAs “in many cases” overlap at uncertainty. The LA-ICPMS dates are “systematically younger” than the paired CA-ID-TIMS dates, and intransigent Pb loss was attributed to some of the CA-ID-TIMS dates (Rasmussen et al., 2021).

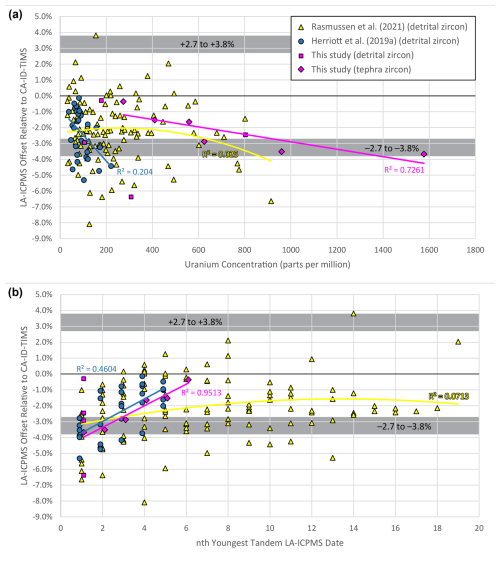
Figure 9 Percent-offset plots of laser ablation–inductively coupled plasma mass spectrometry (LA-ICPMS) dates as benchmarked by tandem chemical abrasion–isotope dilution–thermal ionization mass spectrometry (CA-ID-TIMS) results from Herriott et al. (2019a), Rasmussen et al. (2021), and this study. Data are detrital zircon (n=144 grains) except for the tephra zircon (n=6 grains) results from Ninuluk Bluff (this study). (a) Percent offset versus uranium concentration. (b) Percent offset versus nth youngest tandem LA-ICPMS date (a grain that yielded the youngest LA-ICPMS date that was subsequently dated by CA-ID-TIMS is the nth=1st youngest tandem LA-ICPMS date). Symbols are the same as in (a). All best-fit trend lines are linear, except for the Rasmussen et al. (2021) data, which are fitted with a second-order polynomial regression. Wide gray bars depict the range of average uncertainty (±2σ at Y) envelope edges for the plotted data (±2.7 %–3.8 % per study; see text and Fig. 10).

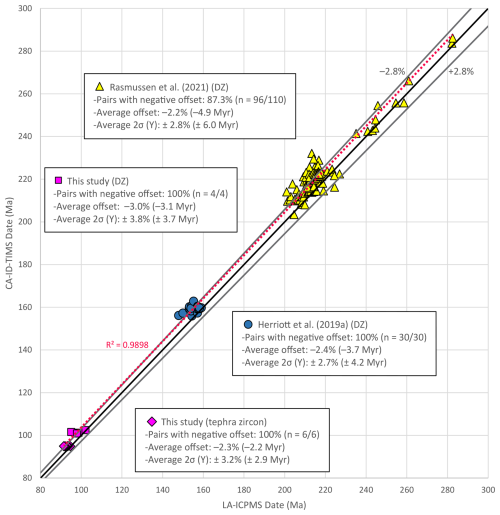
Figure 10 Cross-plot of tandem laser ablation–inductively coupled plasma mass spectrometry (LA-ICPMS) and chemical abrasion–isotope dilution–thermal ionization mass spectrometry (CA-ID-TIMS) results from Herriott et al. (2019a), Rasmussen et al. (2021), and this study. Approximately 90 % of the data bear negative offsets, where LA-ICPMS dates are younger than paired CA-ID-TIMS dates. The 1:1 black line marks the zero offset for date pairs; +2.8 % and −2.8 % gray lines delineate the average (all plotted data) uncertainty window (±2σ at Y). Unbiased datasets should cluster along the 1:1 line, yet it is the −2.8 % line that most closely coincides with the linear (dotted red) trend line fit to all the data.

Herriott et al. (2019a) presented LA-ICPMS–CA-ID-TIMS tandem-date pairs (n=30; Fig. 2 therein) for 6 DZ samples from the Middle–Upper Jurassic Chinitna and Naknek formations (Alaska, USA), which were deposited in a forearc basin associated with active magmatism. The 30 tandem-date pairs plotted in Fig. 2 of Herriott et al. (2019a) have LA-ICPMS results that are single-grain, multiple-analysis, weighted-mean dates. Negative offsets are universal: 30 of 30 LA-ICPMS dates are younger than their paired CA-ID-TIMS dates, with average overall offsets of −2.4 % and −3.7 Myr (Figs. 9 and 10). For reference, the average reported 2σ uncertainty (Y) for the 30 tandem (multiple analyses; n=3 per grain) LA-ICPMS dates is ±2.7 % and ±4.2 Myr. Average offsets for the 6 youngest single grain with multiple-analysis (YSGMA (all tandem-dated)) LA-ICPMS-based maximum depositional dates (MDDs sensu Herriott et al., 2019a) are −3.8 % and −6.0 Myr, with all YSGMAs being younger than the paired CA-ID-TIMS dates, and only 1 of 6 of these date pairs overlaps at 2σ (Y) (Herriott et al., 2019a; Fig. 2 therein). Herriott et al. (2019a) interpreted a residual bias in their LA-ICPMS multiple-analysis results due to Pb loss. Youngest statistical population (YSP sensu Coutts et al., 2019) MDDs were noted as generally yielding results consistent with the CA-ID-TIMS-based MDAs (Herriott et al., 2019a).

Zircon with higher U (and Th) concentrations accumulates more radiation damage per unit time than zircon with lower concentrations, and radiation damage can be a proxy for, and mechanism of, Pb loss (and matrix effects), although geologic annealing can impart complexity to these relations (e.g., Herrmann et al., 2021). Tandem data of Figs. 9 and 10 are mostly from zircon with moderate to low U concentrations (94 % are <600 ppm U), with only 15 % of the tandem YSG/YSGMA DZ having U concentrations >350 ppm. Although most trend lines of Fig. 9a reveal poor goodness-of-fit values, each line does indicate increasing (absolute value) negative offsets with increasing U concentration. Despite the potential causal relation between the percent offset and U concentration, any U-based date filtering tactic seems unlikely to meaningfully mitigate the magnitude and pervasiveness of young biases in the tandem LA-ICPMS dates. Nevertheless, viewing tandem-dating offset relations relative to U values – or, ideally, alpha dose determinations (McKanna et al., 2024) – may be a way to gain further insight into open-system behavior.

The Triassic and Jurassic datasets in Fig. 9b adhere to a similar pattern of overall decreasing offset with increasing nth youngest tandem LA-ICPMS date, although neither trend line achieves coincidence with 0 % offset at the highest nth tandem dates. The Herriott et al. (2019a) data improve rapidly with increasing nth youngest tandem date, but the trend is abruptly clipped at the highest nth (fifth) date per sample. The Rasmussen et al. (2021) data do level out at approximately −1.5 % offset (Fig. 9b) by $n\text{th}=\sim \mathrm{10}$th with a polynomial (second-order) trend line, but the nth youngest tandem LA-ICPMS date is not the nth youngest LA-ICPMS date per sample for that dataset (Fig. 11), so the significance of the relations is less clear. These data suggest that tandem-dating studies that aim to improve LA-ICPMS by more fully characterizing offset relations and their trends thru ranked date ordering should consider multiple analyses by LA-ICPMS, higher n (e.g., n=12–20) follow-up with CA-ID-TIMS, and/or methodically broadly sampling (i.e., plucking for tandem CA-ID-TIMS dating) across dense LA-ICPMS date distributions to more comprehensively delineate percent-offset trends for (ideally) single geologic populations, although the latter is difficult to do for DZ samples. Understanding where offset plateaus or inflections may be achieved at higher nth youngest LA-ICPMS dates may reveal distinct or cumulative sources of bias and/or resolve certain offset contributions.

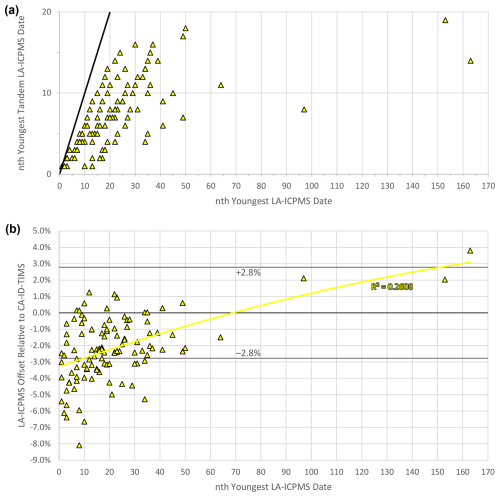
Figure 11 Plots highlighting the context of sampling broadly across laser ablation–inductively coupled plasma mass spectrometry (LA-ICPMS) date distributions for follow-up (tandem) dating by chemical abrasion–isotope dilution–thermal ionization mass spectrometry (CA-ID-TIMS). Data plotted are from Rasmussen et al. (2021), with additional date-rank context from Gehrels et al. (2020). (a) Youngest tandem LA-ICPMS date versus youngest LA-ICPMS date, with the bold black line representing 1-to-1, chronologically sequential sampling for isotope dilution tandem dating from in situ youthful zircon date distributions. Most of the tandem CA-ID-TIMS analyses were conducted on grains with LA-ICPMS dates that range across the youngest $\sim \mathrm{1}/\mathrm{3}$ to $\sim \mathrm{2}/\mathrm{3}$ of dates within young shoulders of the youngest probability density plot modes, which for the plotted samples are generally major modes with relatively dense sampling of youthful populations by LA-ICPMS (see data tables of Gehrels et al., 2020; Rasmussen et al., 2021). (b) Percent offset versus nth youngest LA-ICPMS date. Notably different trend lines (second-order polynomial) between this plot and the same data in Fig. 9b are reflecting the difference between nth youngest LA-ICPMS date (here) and the nth youngest tandem LA-ICPMS date (Fig. 9b); as an example, if grains that yielded the 5th youngest and 10th youngest LA-ICPMS dates were subsequently selected as the (ostensibly) youngest two zircons for dating by CA-ID-TIMS, then those two zircons are nth=5th and 10th “youngest LA-ICPMS date” but are nth=1st and 2nd “youngest tandem LA-ICPMS date”. The 30 date pairs from Herriott et al. (2019a; Fig. 2 therein) are not plotted here but would lie on the 1:1 line of (a) due to their experimental design (i.e., plotting those data in b would be the same as in Fig. 9b). The +2.8 % and −2.8 % gray lines delineate the average uncertainty window (±2σ at Y).

Treatment of the Chinle Formation (and associated Permo-Triassic strata) DZ data by Gehrels et al. (2020), Rasmussen et al. (2021), and Vermeesch (2021) demonstrates the significance of MDA algorithm selection. Gehrels et al. (2020) described how well their MLA MDAs compared to the CA-ID-TIMS-based MDAs (Fig. 13 therein) while also noting that the MLAs were older than the LA-ICPMS-based MDAs of Rasmussen et al. (2021). Vermeesch (2021) reported that MLA performed better than any other MDA algorithm assessed therein, using the tandem-dated Chinle study samples as a test dataset. Rasmussen et al. (2021) concluded “that obtaining a reliable maximum depositional age from LA-ICP-MS analyses is not straightforward and that this approach can lead to greater uncertainties than is often appreciated.” Our percent-offset and date-rank trend analysis further highlights the difficulty of deriving accurate and valid LA-ICPMS-based MDAs from biased data (Figs. 9–11). In fact, Vermeesch (2021) noted that none of the existing LA-ICPMS MDA algorithms, including MLA, can “detect” Pb loss, which violates current MDA model assumptions.

Offset relations from the Herriott et al. (2019a) data suggest similar challenges to obtaining accurate LA-ICPMS-based MDAs. The sampling density of the Jurassic youthful DZ populations by LA-ICPMS is relatively high, and a single-grain MDA-based chronostratigraphic framework derived from those in situ data would be inaccurate at ±2σ (Y). Although Herriott et al. (2019a) did not place chronostratigraphic significance on their LA-ICPMS results, they did suggest that LA-ICPMS-based MDA studies consider favoring YSP (or YC2σ) because of the statistical underpinnings and tendency to coincide with their CA-ID-TIMS-based MDAs. However, that recommendation is subject to the same assessment noted in the previous paragraph: any typical LA-ICPMS-based MDA interpretive tactic would likely include dates that bear systematic and/or geologic biases – near and beyond ±2σ (Y; Fig. 10) – that current algorithms, including YSP, cannot validly mitigate.

The tandem DZ date pairs of our case study only sparsely sample youthful populations, yet they also conform to the trends of the previously published studies. Average LA-ICPMS offsets for the 4 Slope Mountain DZ date pairs are −3.0 % and −3.1 Myr (Fig. 10), ranging from −0.3 % to −6.4 % and from −0.3 to −6.5 Myr (Table 1; Fig. 9); for reference, the average reported uncertainties (2σ at Y) for the tandem DZ LA-ICPMS dates are ±3.8 % and ±3.7 Myr. This pairwise bias suggests that the LA-ICPMS DZ dates not only reflect random scatter during analysis but also include a source of error that will always yield younger dates (e.g., Pb loss) or be systematically prone to rendering a young bias in Mesozoic zircon (e.g., matrix effects; see below). Again removing the geologic complexities tied to DZ, the Ninuluk Bluff tephra zircon date pairs (n=6) have average LA-ICPMS offsets of −2.3 % and −2.2 Myr (Fig. 10), ranging from −0.36 % to −3.68 % and from −0.34 to −3.49 Myr (Table 2; Fig. 9); for reference, the average reported uncertainties (2σ at Y) for the tandem tephra zircon LA-ICPMS dates are ±3.2 % and ±2.9 Myr. The tephra zircon date distributions (LA-ICPMS and CA-ID-TIMS) are consistent with analytical dispersion among a single population as resolved by the methods, but the LA-ICPMS results have pervasive negative offsets (Table 2; Fig. 7), demonstrating that U–Pb geochronologic challenges for LA-ICPMS are not unique to DZ (see also Tian et al., 2022; Howard et al., 2025). Although Pb loss is the most widely cited cause for young bias in DZ MDA case studies, variable ablation behavior is an additional candidate source of negative offset for LA-ICPMS data that is examined in the following section.

3.1.3 Variable ablation behavior

Inter-elemental mass fractionation occurs during U–Pb LA-ICPMS analysis, requiring sample-standard bracketing to correct isotope ratios for unknowns (e.g., Schaltegger et al., 2015). The unknown analyses (i.e., sample; e.g., DZ) are fractionation-corrected based on a primary standard/reference zircon (e.g., Plešovice, R33, Temora-2, 91500; e.g., Eddy et al., 2019; Sundell et al., 2021) and checked by validation (e.g., secondary, tertiary) references, which are treated as unknowns, commonly selected from the same suite of well-characterized reference zircon, and generally regarded as an accuracy and/or reproducibility assessment for the LA-ICPMS analyses (e.g., Gehrels et al., 2008, 2020). Variable ablation behavior (i.e., matrix effects) between primary reference and sample zircon analyzed by LA-ICPMS can render biases in inter-element fractionation-corrected U–Pb ratios (and dates) of the unknowns (e.g., Schoene, 2014). Thus, systematic errors in laser- and plasma-induced elemental fractionation are critical uncertainty sources in the LA-ICPMS U–Pb geochronology of zircon (e.g., Košler et al., 2013; Sliwinski et al., 2017, 2022; Ver Hoeve et al., 2018) and may impact MDA case studies.

Matrix effects are generally attributed to physical and chemical properties of zircon (radiation damage, crystallinity, crystallography, trace element substitution, opacity, texture, etc.), with experimental studies exploring various potential factors and mitigation measures (Black et al., 2004; Allen and Campbell, 2012; Crowley et al., 2014; Marillo-Sialer et al., 2014, 2016; Steely et al., 2014; von Quadt et al., 2014; Solari et al., 2015; Sliwinski et al., 2017, 2022; Ver Hoeve et al., 2018; Donaghy et al., 2024). Instrumental settings can also impact ablation behavior, as reviewed by Schaltegger et al. (2015; see also Sliwinski et al., 2022). Regardless, a typical view of sample-standard bracketing for ${}^{\mathrm{206}}\mathrm{Pb}{/}^{\mathrm{238}}\mathrm{U}$ geochronology of zircon by LA-ICPMS is that it generally performs well, although a commonly cited ∼1 %–2 % systematic, reference material variability uncertainty for LA-ICPMS currently sets precision and accuracy limits for the method (e.g., Gehrels et al., 2008; Schoene, 2014; Horstwood et al., 2016; Sliwinski et al., 2022).

There are indications that Meso-Cenozoic zircons are prone to having negative offsets tied to matrix effects. Experiments by Allen and Campbell (2012) revealed that LA-ICPMS-based ${}^{\mathrm{206}}\mathrm{Pb}{/}^{\mathrm{238}}\mathrm{U}$ dates for their Cretaceous and Cenozoic zircon bore the greatest offsets, ranging from −5.1 % to 0 % (see also Klötzli et al., 2009). Comparisons between LA-ICPMS and ID-TIMS or CA-ID-TIMS dates/ages for reference zircon suggest that some of the least well behaved reference zircon (when treated as unknowns) are the relatively few that are of Meso-Cenozoic age (e.g., Donaghy et al., 2024, Fig. 1 therein), with negative offsets being common in many compilations (Gehrels et al., 2008, Fig. 10 therein; Schoene, 2014, Fig. 11 therein; Sundell et al., 2021, Fig. 5 therein; Sliwinski et al., 2022). These relations may in part reflect the fact that older primary reference zircon and/or primary reference zircon with higher U (and Th) concentrations is dated relative to younger unknown zircon and/or unknown zircon with lower U (and Th) concentrations (Allen and Campbell, 2012). As noted above, geologic annealing, which heals radiation damage, can complicate this simplified framework. Either way, one implication is that primary reference zircon with higher degrees of accumulated radiation damage may ablate at faster rates than unknown zircon with lower degrees of radiation damage, potentially rendering a young bias in the unknowns (e.g., Sliwinski et al., 2017, 2022), although additional controls on ablation rate variability have also been noted (e.g., Marillo-Sialer et al., 2014, 2016). Nevertheless, employing reference materials with a similar matrix character to that of unknowns and laboratory thermal annealing of references and unknowns may be considered best practices for mitigating this source of uncertainty (e.g., Mattinson, 2005; Allen and Campbell, 2012; Solari et al., 2015; Marillo-Sialer et al., 2016; Ver Hoeve et al., 2018; Herriott et al., 2019a).

Interestingly, for some of the younger reference zircons analyzed by Sundell et al. (2021; e.g., FCT, Fig. 5 therein), their rapid-acquisition LA-ICPMS results are overall more accurate (though less precise) than more conventional (i.e., longer) acquisition rates, leading those authors to suggest that limiting ablation time (per spot) could render “better analytical results in some cases” due to limiting the relative impact of “down-hole fractionation and compositional heterogeneity” (i.e., matrix effects) on the resultant data. And chemical abrasion pre-treatment for LA-ICPMS zircon geochronology has been demonstrated to reduce ablation rates and thus pit depth for any given ablation duration (Crowley et al., 2014; Donaghy et al., 2024), suggesting that chemical abrasion–LA-ICPMS not only provides Pb-loss mitigation but also can diminish down-hole fractionation and may reduce matrix-effect impacts. Future experiments might further evaluate thermal annealing versus full chemical abrasion pre-treatments for LA-ICPMS zircon geochronology to distinguish, for example, the benefits of increased crystal density and normalizing of ablation behavior among references and unknowns for thermal annealing alone from the potential additional influence of acid leaching on diminished coupling (and resultant reduced pit depths) with the laser (Crowley et al., 2014; see also Ver Hoeve et al., 2018).

The general analytical context for fractionation-corrected LA-ICPMS ratios (and dates) of sampled zircon is clearly relevant to DZ MDAs employed in chronostratigraphic work. Most of the tandem LA-ICPMS data plotted here lie between approximately −6 % and +1 % offset (Fig. 9), with averages per tandem dataset of −2.2 % to −3.0 % (Fig. 10), which is generally consistent with the large compilation and findings of Howard et al. (2025). Even the above-noted LA-ICPMS–(CA-)ID-TIMS U–Pb datasets of reference zircon suggest that biases tied to matrix effects should not be ignored for Meso-Cenozoic zircon and can be of sufficient magnitude to detrimentally impact interpretations (Herriott et al., 2019a). It is critical for practitioners to appreciate that reference-material-related errors or variance factors do not – and effectively cannot – quantify how well the fractionation corrections perform for unknown zircon (e.g., Sliwinski et al., 2017; also Ruiz et al., 2022; Puetz and Spencer, 2023). And validation material results are similarly not an explicit assessment of the accuracy and/or reproducibility of LA-ICPMS analyses of unknowns, but rather they serve as an important yet general proxy for LA-ICPMS performance during a session. Tandem dating does, however, provide an independent and direct benchmark for unknowns.

Finally, it may be that higher U (and Th) zircons are less susceptible to matrix-effect-related offsets (Allen and Campbell, 2012), but an all-things-being-equal increase in radiation damage is conducive to Pb loss. And in our case study and the work by Herriott et al. (2019a), all analyzed zircons were thermally annealed prior to LA-ICPMS in an attempt to diminish variable ablation behavior among unknowns and references, yet data from both of those studies and the independent work by Rasmussen et al. (2021) exhibit nearly ubiquitous negative offsets of comparable (percent) magnitudes (Fig. 10). There are many factors that affect the degree to which thermal annealing may improve results, and establishing that improved accuracy has been achieved is not typically demonstrable in routine studies (Horstwood et al., 2016). And, for the Ninuluk Bluff tephra data, the linear correlations between increasing (absolute value) percent negative offset and increasing U concentration (Fig. 9a), as well as decreasing (absolute value) percent negative offset and increasing nth youngest tandem date (Fig. 9b), are the best goodness-of-fit results for any of the tandem datasets presented and reviewed here and are suggestive of a causal link. However, a conventional, radiation-damage-based view of Pb loss to account for such a correlation should be expanded to also consider a matrix-effect component or control.

3.2 Justification for benchmarking with CA-ID-TIMS

U–Pb zircon geochronology by CA-ID-TIMS is a cornerstone of high-precision chronostratigraphy (e.g., Bowring et al., 2006; Schmitz et al., 2020; Schoene et al., 2021; Wang et al., 2023). The past two decades have brought breakthroughs in ID-TIMS with the advent of chemical abrasion for zircon (Mattinson, 2005) and tracer solution advancements (Condon et al., 2015; McLean et al., 2015). ID-TIMS zircon geochronology has improved beyond the <0.1 % precision and accuracy barrier, with the <0.01 % threshold on the horizon (Schaltegger et al., 2021). Analytical dispersion does occur in CA-ID-TIMS experiments (e.g., McLean et al., 2015; Horstwood et al., 2016; Spencer et al., 2016; Klein and Eddy, 2024; Condon et al., 2024), although the precision of the measurements is improved by ∼1–2 orders of magnitude relative to LA-ICPMS (e.g., Schoene, 2014; Schaltegger et al., 2015, 2021) such that the method may resolve geologic processes of interest for Meso-Cenozoic zircon. CA-ID-TIMS dates are also less likely to bear systematic offsets than microbeam data are, with isotope dilution permitting elemental fractionation corrections via well-calibrated synthetic tracer solutions, eliminating the sample-standard bracketing – and matrix-effect uncertainties – of in situ methods (e.g., Schoene, 2014; Ramezani et al., 2022). Pb loss can impact zircon analyzed by CA-ID-TIMS (e.g., Schoene, 2014; Keller et al., 2018, 2019; Widmann et al., 2019; Rasmussen et al., 2021; Schaltegger et al., 2021; McKanna et al., 2023, 2024), although some potential points of failure for chemical abrasion (Mattinson, 2011, and references therein) reflect significant Pb loss and/or extensive radiation damage. Recent advancements have also permitted CA-ID-TIMS analyses of fragments from the same zircon crystal (e.g., Schmitz et al., 2020; Gaynor et al., 2022), and separately dating multiple fragments per zircon crystal is a practical, empirical means of rooting out potentially spurious results and increasing confidence that critically young CA-ID-TIMS DZ dates that underpin MDAs are not impacted by Pb loss (e.g., Herriott et al., 2019a; Karlstrom et al., 2020; this study).

There is thus reasonable justification for benchmarking LA-ICPMS zircon dates with CA-ID-TIMS ages (i.e., reference values) from the same crystals; however, increased understanding of Pb loss and how chemical abrasion performs in zircon (including DZ) with perhaps subtle, near-zero-age, low-temperature Pb loss would further bolster such benchmarking. Although Pb lost from damaged portions of zircon is typically mitigated by chemical abrasion, the pre-treatment may not remove recrystallized or overgrowth domains (e.g., Gaynor et al., 2022, and references therein). Thus, avoiding altered zones and/or overgrowths, which can result from low-temperature alteration and/or metamorphic processes, is important in establishing accurate CA-ID-TIMS-based DZ MDAs (e.g., Ruiz et al., 2022, and references therein).

4 Summary

The late Albian DZ MDAs from Slope Mountain provide high-precision age constraints for the Nanushuk–Torok clinothem along its southern outcrop belt. The Ninuluk Bluff tephra zircon age is associated with a sequence stratigraphically significant transgression (Lease et al., 2022) and provides a minimum age constraint for the Nanushuk Formation at Slope Mountain, which we bracket as $\le \mathrm{101.58}\pm \mathrm{0.13}$ (0.14) [0.18] Ma and $\ge \mathrm{94.909}\pm \mathrm{0.032}$ (0.042) [0.110] Ma. Collectively, these interpretations render geologically sensible minimum stratigraphic accumulation rates (∼120–150 m Myr⁻¹) and indicate a reduced (>50 %) window of Nanushuk sedimentation at Slope Mountain relative to the wide-ranging biostratigraphy (Fig. 8). Furthermore, the Slope Mountain CA-ID-TIMS results establish that the tandem LA-ICPMS data have young bias that would render a geologically implausible and inaccurate – at 2σ at Y – framework if they had been integrated as YSG (LA-ICPMS) MDAs in a chronostratigraphic analysis. The Ninuluk Bluff tephra zircon data also have offsets for the paired LA-ICPMS results, with weighted means that are inaccurate at 2σ at Y (Fig. 7), indicating that young bias is not only a challenge for DZ geochronology and demonstrating that analytically seemingly well behaved and well clustered LA-ICPMS data can nevertheless bear total geochronologic uncertainty that may not be adequately accounted for by quantified confidence intervals.

We considered three candidate offset sources for LA-ICPMS U–Pb zircon dates:

1. Analytical dispersion in LA-ICPMS data will impart YSGs with increasing (absolute value) negative offsets as youthful-population sampling density increases. It is generally difficult to defend relying on YSG MDAs, which in lower-n population sampling may lie within the 2σ uncertainty window of – but are systematically prone to be younger than – the true age of the dated DZ. Typical LA-ICPMS ranked-date-based selection of DZ crystals for tandem dating will also benchmark increasing (absolute value) magnitudes of analytical-dispersion-sourced negative offsets as youthful-population sampling density increases. Measurement uncertainty is a relatively simple source of potential MDA error but can be difficult to disentangle from other sources of offset or geologic mixing of DZ populations. Our exploration of the perils of analytical uncertainty for establishing accurate single-grain LA-ICPMS MDAs from moderate-precision microbeam data also starkly highlights how using a TDA as the reference value for MDA accuracy is invalid regardless of youthful-population sampling density, MDA algorithm preferences, or analytical technique.

2. Identifying Pb loss for LA-ICPMS analyses of Meso-Cenozoic zircon is difficult because discordance cannot be meaningfully assessed. Thus, mitigating Pb loss from zircon is imperative. Although mitigation methods for in situ U–Pb methods are not yet well established, chemical abrasion LA-ICPMS is poised to become more routine and beneficial to DZ MDA studies (Donaghy et al., 2024; Sharman and Malkowski, 2024; Howard et al., 2025). Pb loss under common conditions in sedimentary basins and outcrops, including zircon residence in water (Keller et al., 2019) at less than geologic annealing temperatures (Herrmann et al., 2021), could be a culprit for what might be subtle and pervasive Pb loss in DZ (e.g., Andersen et al., 2019; Andersen and Elburg, 2022; Sharman and Malkowski, 2024; Howard et al., 2025).

3. Variable ablation behavior (i.e., matrix effects) can impact the accuracy of laser ablation zircon geochronology (e.g., Allen and Campbell, 2012; Sliwinski et al., 2022). Klötzli et al. (2009) demonstrated the significance of the primary reference zircon for, and its influence on, reported dates and accuracy for LA-ICPMS. CA-ID-TIMS dating of unknowns uses internal isotope dilution based on well-calibrated tracer solutions, eliminating the laser-ablation-related matrix effects of LA-ICPMS that result from variation among reference and sample zircon crystals, further bolstering the complementary benefits of tandem dating. Propagating systematic uncertainties is one key to avoiding over-interpreting dates/ages, but standard calibration uncertainties or excess-variance factors for reference zircon are not quantified characterizations of the variance of unknown zircon. The “extended error” approach and discussion of Ruiz et al. (2022) comprise a reminder that systematic uncertainties are perhaps under-characterized for LA-ICPMS U–Pb dating of unknown zircon.

5 Conclusions and future directions

The goal for establishing DZ MDAs is to sample the youngest zircon population in a sedimentary rock and determine its true age. The potential chronostratigraphic significance of an MDA will depend on a complex series of factors, with the most significant results being derived by successfully sampling and accurately dating youthful populations with minimal crystallization–sedimentation lag times. The accuracy of an MDA is quantitatively determined via a reference age of crystallization (e.g., by tandem dating) for the youngest analyzed DZ population and cannot be quantitatively ascertained by chronostratigraphic benchmarking due to the one-sided (maximum) detrital (principle of inclusions) context. Obtaining LA-ICPMS DZ MDAs that overlap CA-ID-TIMS MDAs is commonly achieved (e.g., Herriott et al., 2019a; Gehrels et al., 2020; Rasmussen et al., 2021; Vermeesch, 2021), but the accuracy and validity of results obtained from biased datasets (Figs. 9–11; Howard et al., 2025) should be queried. A simple overlap-at-uncertainty (e.g., 2σ) accuracy criterion is reasonable for any single result, but it is harder to justify that tactic when assessing larger or compiled datasets and offset trends for their broader implications because it can stymie further advancements. Even with LA-ICPMS offset averages lying within – yet near the negative edges of – ±2σ (Y) intervals (Fig. 10), we anticipate that many researchers will not be satisfied with the offset plots of this study and of Howard et al. (2025), and efforts to improve accuracy for LA-ICPMS zircon geochronology will be fruitful.

We recommend a shift in evaluating LA-ICPMS-based MDAs toward considering the broad validity of the algorithms: i.e., the capability of the metrics to accurately measure what they are intended to measure. Accurate and valid MDAs are derived from analytically, statistically, and geologically defensible algorithms, and because we do not currently have Pb-loss-aware (see Keller, 2023) or matrix-effect-aware LA-ICPMS DZ MDA algorithms (see also Sharman and Malkowski, 2024), the underlying data should not bear systematic or geologic biases. LA-ICPMS-based single-grain MDAs are problematic because numerous sources of error, including the magnitude and distribution of analytical dispersion, Pb loss, and matrix effects, collectively render n=1 grain MDAs (e.g., YSG) with maximized (absolute value) young-bias potential. Adhering to the philosophically defensible ideal of single-crystal DZ MDAs, as recommended by Copeland (2020), is best paired with CA-ID-TIMS. Furthermore, accurate and valid multi-grain LA-ICPMS MDAs will be more commonly achievable as LA-ICPMS U–Pb geochronology accuracy improves (cf. Puetz and Spencer, 2023).

LA-ICPMS fueled the DZ revolution, but the uncertainty sources for LA-ICPMS dates explored in this paper suggest that follow-up analyses by CA-ID-TIMS will become more common in MDA studies where the accuracy and precision are poised to resolve the research questions posed. And the future remains bright for microbeam-based MDAs. Intra- and inter-lab tandem-dating experiments may definitively deconvolve error components in LA-ICPMS. Further understanding how low-temperature Pb loss may impact LA-ICPMS DZ dates – and how chemical abrasion performs in mitigating Pb loss for LA-ICPMS ages from young zircon (e.g., Donaghy et al., 2024; Sharman and Malkowski, 2024) – is a similarly critical and promising pursuit. CA-ID-TIMS MDAs now bear on considerations of geologic timescale refinements (e.g., Herriott et al., 2019a; Karlstrom et al., 2020; Cothren et al., 2022), and Bayesian modeling conditioned with high-precision U–Pb tephra ages, as well as DZ MDAs, in a superpositional, age–depth context is a notable development in deep-time chronostratigraphic research (e.g., Schoene et al., 2019; Trayler et al., 2020; Landing et al., 2021). For current DZ MDA work, tandem dating is available today, with screening for youthful zircon by LA-ICPMS and establishing MDAs by CA-ID-TIMS. “The best of both worlds” (Mattinson, 2013) benefits of tandem dating are evident, but integrating CA-ID-TIMS into DZ case studies requires careful consideration of project budgets, experimental designs, and collaboration opportunities.